Bài 11 trang 102 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 6: Ba đường conic

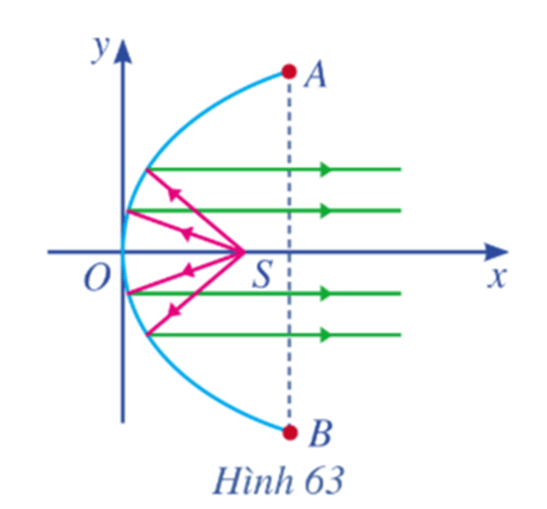
Bài 11 trang 102 Toán lớp 10 Tập 2: Một chiếc đèn có mặt cắt ngang là hình parabol (Hình 63). Hình parabol có chiều rộng giữa hai mép vành là AB = 40 cm và chiều sâu h = 30 cm (h bằng khoảng cách từ O đến AB). Bóng đèn nằm ở tiêu điểm S. Viết phương trình chính tắc của parabol đó.

Lời giải:

Phương trình chính tắc của parabol có dạng y² = 2px (với p > 0).

Vì AB = 40 và Ox là đường trung trực của đoạn AB nên khoảng cách từ điểm A đến trục Ox là $\frac{40}{2}=20$.

Chiều sâu h bằng khoảng cách từ O đến AB và cũng chính bằng khoảng cách từ điểm A đến trục Oy và bằng 30.

Do đó, parabol đi qua điểm A có hoành độ là 30 (khoảng cách từ A đến trục Oy) và tung độ là 20 (khoảng cách từ A đến trục Ox) hay A(30; 20).

Thay tọa độ điểm A vào phương trình chính tắc của parabol, ta được:

20² = 2p . 30 ⇔ 60p = 400 ⇔ p = $\frac{20}{3}$ (thỏa mãn p > 0).

Lời giải Toán 10 Bài 6: Ba đường conic hay, chi tiết khác: