Bài 4 trang 31 Toán 11 Tập 1 Cánh diều

Giải Toán 11 Bài 3: Hàm số lượng giác và đồ thị - Cánh diều

Bài 4 trang 31 Toán 11 Tập 1: Dùng đồ thị hàm số, hãy cho biết:

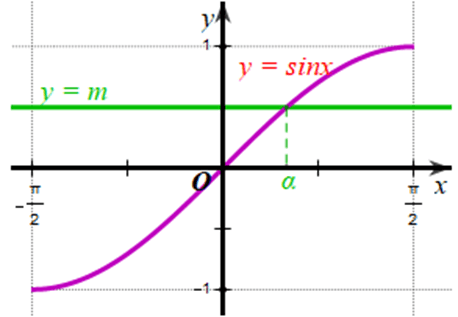
a) Với mỗi m ∈ [‒1;1], có bao nhiêu giá trị $\alpha \in \left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ sao cho sinα = m;

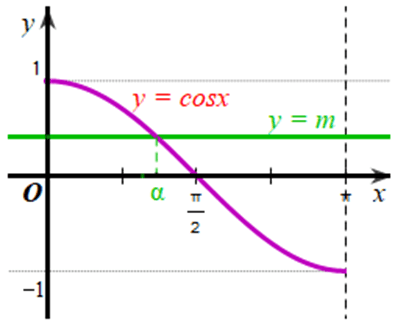
b) Với mỗi m ∈ [‒1;1], có bao nhiêu giá trị α ∈ [0; π] sao cho cosα = m;

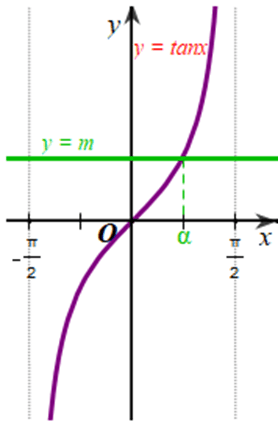
c) Với mỗi m ∈ ℝ, có bao nhiêu giá trị $\alpha \in \left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ sao cho tanα = m;

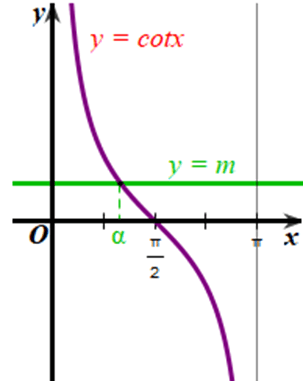
d) Với mỗi m ∈ ℝ, có bao nhiêu giá trị α ∈ (0; π) sao cho cotα = m.

Lời giải:

a) Xét đồ thị hàm số y = m (m ∈ [‒1;1]) và đồ thị hàm số y = sinx trên :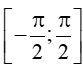

Từ đồ thị của hai hàm số ở hình vẽ trên, ta thấy với mỗi m ∈ [‒1;1] thì hai đồ thị cắt nhau tại 1 điểm.

Vậy với mỗi m ∈ [‒1;1] sẽ có 1 giá trị 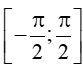$\alpha \in$ sao cho sinα = m.

b) Xét đồ thị hàm số y = m (m ∈ [‒1;1]) và đồ thị hàm số y = cosx trên [0; π]:

Từ đồ thị của hai hàm số ở hình vẽ trên, ta thấy với mỗi m ∈ [‒1;1] thì hai đồ thị cắt nhau tại 1 điểm.

Vậy m ∈ [‒1;1] sẽ có 1 giá trị α ∈ [0; π] sao cho cosα = m.

c) Xét đồ thị hàm số y = m (m ∈ ℝ) và đồ thị hàm số y = tanx trên $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$:

Từ đồ thị của hai hàm số ở hình vẽ trên, ta thấy với mỗi m ∈ ℝ thì hai đồ thị cắt nhau tại 1 điểm.

Vậy với mỗi m ∈ ℝ sẽ có 1 giá trị $\alpha \in \left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ sao cho tanα = m.

d) Xét đồ thị hàm số y = m (m ∈ ℝ) và đồ thị hàm số y = cotx trên (0; π):

Từ đồ thị của hai hàm số ở hình vẽ trên, ta thấy với mỗi m ∈ ℝ thì hai đồ thị cắt nhau tại 1 điểm.

Vậy với mỗi m ∈ ℝ sẽ có 1 giá trị α ∈ (0; π) sao cho cotα = m.

Lời giải bài tập Toán 11 Bài 3: Hàm số lượng giác và đồ thị hay, chi tiết khác: