Bài 4.24 trang 84 Toán 7 Tập 1 - Kết nối tri thức

Giải Toán 7 Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng

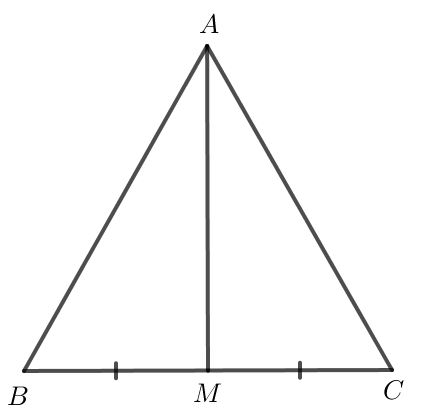
Bài 4.24 trang 84 Toán 7 Tập 1: Cho tam giác ABC cân tại A và M là trung điểm của đoạn thẳng BC. Chứng minh AM vuông góc với BC và AM là tia phân giác của góc BAC.

Lời giải:

Do tam giác ABC cân tại A nên AB = AC.

Do M là trung điểm của BC nên MB = MC.

Xét hai tam giác ABM và ACM có:

AB = AC (chứng minh trên).

AM chung.

MB = MC (chứng minh trên).

Do đó $\Delta ABM=\Delta ACM$ (c – c – c).

Khi đó $\widehat{AMB}=\widehat{AMC}$ (2 góc tương ứng).

Mà $\widehat{AMB}+\widehat{AMC}=180°$ (2 góc kề bù) nên $\widehat{AMB}=\widehat{AMC}=90°.$

Do đó $AM\perp BC.$

Do $\Delta ABM=\Delta ACM$ nên $\widehat{BAM}=\widehat{CAM}$ (2 góc tương ứng).

Do đó AM là tia phân giác của $\widehat{BAC}.$

Vậy AM vuông góc với BC và AM là tia phân giác của góc BAC.

Lời giải bài tập Toán 7 Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng hay khác: