Bài 7.17 trang 53 Toán 11 Tập 2 - Kết nối tri thức

Giải Toán 11 Bài 25: Hai mặt phẳng vuông góc - Kết nối tri thức

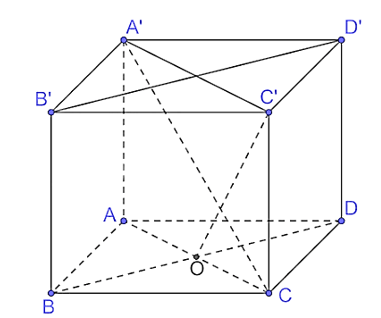
Bài 7.17 trang 53 Toán 11 Tập 2: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a.

a) Tính độ dài đường chéo của hình lập phương.

b) Chứng minh rằng (ACC'A') ⊥ (BDD'B').

c) Gọi O là tâm của hình vuông ABCD. Chứng minh rằng $\widehat{CO{C}^{\text{'}}}$ là một góc phẳng của góc nhị diện [C, BD, C']. Tính (gần đúng) số đo của các góc nhị diện [C, BD, C'], [A, BD,C'].

Lời giải:

a) Vì ABCD.A'B'C'D' là hình lập phương nên có các mặt là hình vuông.

Xét tam giác ABC vuông tại B, có $AC=\sqrt{A{B}^2+B{C}^2}=\sqrt{a^2+a^2}=a\sqrt{2}$.

Vì AA' ⊥ (ABCD) nên AA' ⊥ AC.

Xét tam giác A'AC vuông tại A, có $A^{\text{'}}C=\sqrt{A{A^{\text{'}}}^2+A{C}^2}=\sqrt{a^2+2a^2}=a\sqrt{3}$.

Vậy đường chéo của hình lập phương có độ dài là $a\sqrt{3}$.

b) Vì AA' ⊥ (ABCD) nên AA' ⊥ BD.

Vì ABCD là hình vuông nên AC ⊥ BD mà AA' ⊥ BD, suy ra BD ⊥ (ACC'A').

Vì BD ⊥ (ACC'A') nên (ACC'A') ⊥ (BDD'B').

c) Vì BD ⊥ (ACC'A') nên BD ⊥ C'O mà CO ⊥ BD (do AC ⊥ BD) nên $\widehat{CO{C}^{\text{'}}}$là góc phẳng nhị diện của góc nhị diện [C, BD, C'].

Do ABCD là hình vuông nên O là trung điểm của AC, suy ra $AO=OC=\frac{AC}{2}=\frac{a\sqrt{2}}{2}$.

Xét tam giác C'CO vuông tại C, có $\tan \widehat{C^{\text{'}}OC}=\frac{C{C}^{\text{'}}}{CO}=\frac{a}{\frac{a\sqrt{2}}{2}}=\sqrt{2}$ $\Rightarrow \widehat{C^{\text{'}}OC}\approx 55°$.

Vậy số đo của các góc nhị diện [C, BD, C'] khoảng 55°.

Vì AO ⊥ BD (do AC ⊥ BD), BD ⊥ C'O nên $\widehat{AO{C}^{\text{'}}}$ là góc phẳng nhị diện của góc nhị diện [A, BD,C'].

Vì $\widehat{AO{C}^{\text{'}}}+\widehat{C^{\text{'}}OC}=180°$nên $\widehat{AO{C}^{\text{'}}}=180°-\widehat{C^{\text{'}}OC}\approx 180°-55°=125°$.

Vậy số đo góc nhị diện [A, BD,C'] khoảng 125°.

Lời giải bài tập Toán 11 Bài 25: Hai mặt phẳng vuông góc hay, chi tiết khác: