HĐ2 trang 38 Toán 10 Tập 1 - Kết nối tri thức

Giải Toán 10 Kết nối tri thức Bài 6: Hệ thức lượng trong tam giác

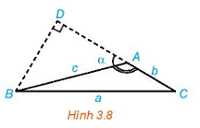
HĐ2 trang 38 Toán 10 Tập 1: Trong Hình 3.8, hãy thực hiện các bước sau để thiết lập công thức tính a theo b, c và giá trị lượng giác của góc A.

a) Tính a² theo BD² và CD².

b) Tính a² theo b, c và DA.

c) Tính DA theo c và cosA.

d) Chứng minh a² = b² + c² – 2bc.cosA.

Lời giải:

a) Xét ΔBDC vuông tại D, có:

BC² = BD² + DC² (Định lí Pythagore)

Hay a² = BD² + DC²

b) Xét ΔBDA vuông tại D, có:

BA² = BD² + DA² (Định lí Pythagore)

Hay BD² = c² - DA²

Ta lại có: DC = DA + AC = DA + b

Khi đó: a² = c² – DA² + (DA + b)² = c² – DA² + DA² + 2.DA.b + b² = c² + b² + 2.DA.b.

Vậy a² = BD² + DC² = c² + b² + 2.DA.b (1)

c) Xét ΔBDA vuông tại D, có:

DA = AB.cosα = c.cosα.

Lại có: $\widehat{BAC}+\widehat{BAD}=180°$ (hai góc kề bù)

Hay $\widehat{BAC}+\alpha =180°\Rightarrow \alpha =180°-\widehat{BAC}$.

Suy ra cosα = $cos\left(180°-\widehat{BAC}\right)$ = – cos $\widehat{BAC}$ = – cosA.

Do đó, DA = – c.cosA. 

d) Thay DA = – c.cosA vào biểu thức (1), ta được:

a² = c² + b² – 2bc.cosA

Vậy a² = b² + c² – 2bc cosA. (đpcm)

Lời giải bài tập Toán 10 Bài 6: Hệ thức lượng trong tam giác hay, chi tiết khác: