Giải Toán 10 | No tags
Với giải bài tập Toán 10 Bài 3: Bất phương trình bậc nhất hai ẩn sách Kết nối tri thức hay nhất, chi tiết giúp học sinh lớp 10 dễ dàng làm bài tập Toán 10 Bài 3.
Video Giải Toán 10 Bài 3: Bất phương trình bậc nhất hai ẩn - Cô Nguyễn Hà Nguyên (Giáo viên VietJack)
Mở đầu
Mở đầu trang 22 Toán 10 Tập 1: Nhân ngày Quốc tế Thiếu nhi 1 – 6, một rạp chiếu phim phục vụ các khán giả của một bộ phim hoạt hình. Vé được bán ra có hai loại:
Loại 1 (dành cho trẻ từ 6 – 13 tuổi): 50 000 đồng/vé;
Loại 2 (dành cho người trên 13 tuổi): 100 000 đồng/vé.
Người ta tính toán rằng, để không phải bù lỗ thì số tiền vé thu được ở rạp chiếu phim này phải đạt tối thiểu 20 triệu đồng. Hỏi số lượng vé bán được trong những trường hợp nào thì rạp chiếu phim phải bù lỗ?
Lời giải:
Sau bài này ta sẽ giải được như sau:
Gọi số lượng vé loại 1 bán được là x (vé) và số lượng vé loại 2 bán được là y (vé) (x,y ∈ ℕ*)
Số tiền thu được là: 50 000x + 100 000y (đồng)
Nếu rạp chiếu phim phải bù lỗ thì số tiền thu được phải nhỏ hơn 20 triệu đồng, nghĩa là:
50 000x + 100 000y < 20 000 000 (1)
Tổng số vé x + y sẽ phụ thuộc vào cặp (x,y) thỏa mãn bất phương trình (1) thì rạp chiếu phim phải bù lỗ
Lời giải bài tập Toán 10 Bài 3: Bất phương trình bậc nhất hai ẩn hay, chi tiết khác:
HĐ1 trang 22 Toán 10 Tập 1: Trong tình huống mở đầu, gọi x là số vé loại 1 bán được và y là số vé loại 2 bán được. Viết biểu thức tính số tiền bán vé thu được (đơn vị nghìn đồng) ở rạp chiếu phim đó theo x và y.
a) Các số nguyên không âm x và y thỏa mãn điều kiện gì để số tiền bán vé thu được đạt tối thiểu 20 triệu đồng?
b) Nếu số tiền bán vé thu được nhỏ hơn 20 triệu đồng thì x và y thỏa mãn điều kiện gì?
Lời giải:
Số tiền bán vé thu được (theo đơn vị nghìn đồng) là: 50x + 100y (nghìn đồng).
a) Để số tiền bán vé thu được đạt tối thiểu 20 triệu đồng thì các số nguyên không âm x và y thỏa mãn: 50x + 100y ≥ 20 000 (1).
b) Để số tiền bán vé thu được nhỏ hơn 20 triệu đồng thì x và y thỏa mãn điều kiện:
50x + 100y < 20 000 (2).
Lời giải bài tập Toán 10 Bài 3: Bất phương trình bậc nhất hai ẩn hay, chi tiết khác:
HĐ2 trang 23 Toán 10 Tập 1: Cặp số (x; y) = (100; 100) thỏa mãn bất phương trình bậc nhất hai ẩn nào trong hai bất phương trình thu được ở HĐ1? Từ đó cho biết rạp chiếu phim có phải bù lỗ hay không nếu bán được 100 vé loại 1 và 100 vé loại 2.
Trả lời câu hỏi tương tự với cặp số (x; y) = (150; 150).
Lời giải:
+) Xét cặp số (x; y) = (100; 100).
- Thay x = 100 và y = 100 vào bất phương trình 50x + 100y ≥ 20 000 ta được: 50.100 + 100.100 ≥ 20 000 ⇔ 15 000 ≥ 20 000 (vô lí).
Do đó cặp số (100; 100) không thỏa mãn bất phương trình 50x + 100y ≥ 20 000.
- Thay x = 100 và y = 100 vào bất phương trình 50x + 100y < 20 000 ta được: 50.100 + 100.100 < 20 000 ⇔ 15 000 < 20 000 (luôn đúng).
Do đó cặp số (100; 100) thỏa mãn bất phương trình 50x + 100y < 20 000.
Vì vậy nếu rạp chiếu phim bán được 100 vé loại 1 và 100 vé loại 2 thì số tiền thu được là 15 triệu đồng và rạp chiếu phim phải bù lỗ.
+) Xét cặp số (x; y) = (150; 150).
- Thay x = 150 và y = 150 vào bất phương trình 50x + 100y ≥ 20 000 ta được: 50.150 + 100.150 ≥ 20 000 ⇔ 22 500 ≥ 20 000 (luôn đúng).
Do đó cặp số (150; 150) thỏa mãn bất phương trình 50x + 100y ≥ 20 000.
- Thay x = 150 và y = 150 vào bất phương trình 50x + 100y ≥ 20 000 ta được 50.150 + 100.150 < 20 000 ⇔ 22 500 < 20 000 (vô lí).
Do đó cặp số (150; 150) không thỏa mãn bất phương trình 50x + 100y < 20 000.
Vì vậy nếu rạp chiếu phim bán được 150 vé loại 1 và 150 vé loại 2 thì số tiền thu được là 22,5 triệu đồng và rạp chiếu phim không phải bù lỗ.
Lời giải bài tập Toán 10 Bài 3: Bất phương trình bậc nhất hai ẩn hay, chi tiết khác:
Luyện tập 1 trang 23 Toán 10 Tập 1: Cho bất phương trình bậc nhất hai ẩn x + 2y ≥ 0.
a) Hãy chỉ ra ít nhất hai nghiệm của bất phương trình trên.
b) Với y = 0, có bao nhiêu giá trị của x thỏa mãn bất phương trình đã cho?
Lời giải:
a) Với x = 1, y = 2, thay vào bất phương trình ta có: 1 + 2.2 = 5 ≥ 0 (luôn đúng)
Suy ra (1;2) là nghiệm của bất phương trình đã cho.
Với x = -2, y = 1, thay vào bất phương trình ta có: -2 + 2.1 = 0 ≥ 0 (luôn đúng)
Suy ra (-2;1) là nghiệm của bất phương trình đã cho.
Với x = 7, y = -2, thay vào bất phương trình ta có: 7 + 2.(-2) = 3 ≥ 0 (luôn đúng)
Suy ra (7;-2) là nghiệm của bất phương trình đã cho.
b) Thay y = 0 vào bất phương trình đã cho ta được: x + 2.0 ≥ 0 ⇔ x ≥ 0.
Vậy với y = 0 thì có vô số giá trị của x mà x ≥ 0 thỏa mãn bất phương trình đã cho.
Lời giải bài tập Toán 10 Bài 3: Bất phương trình bậc nhất hai ẩn hay, chi tiết khác:
HĐ3 trang 23 Toán 10 Tập 1: Cho đường thẳng d: 2x – y = 4 trên mặt phẳng tọa độ Oxy (H.2.1). Đường thẳng này chia mặt phẳng thành hai nửa mặt phẳng.
a) Các điểm O(0; 0), A(-1; 3) và B(-2; -2) có thuộc cùng một nửa mặt phẳng bờ là đường thẳng d không?
Tính giá trị của biểu thức 2x – y tại các điểm đó và so sánh với 4.
b) Trả lời câu hỏi tương tự như câu a với các điểm C(3; 1), D(4; - 1).
Lời giải:
a) Dựa vào hình 2.1 ta thấy các điểm A, O và B thuộc cùng một nửa mặt phẳng bờ là đường thẳng d.
Thay x = 0, y = 0 vào biểu thức 2x – y ta được: 2.0 – 0 = 0 < 4.
Suy ra giá trị biểu thức 2x – y tại điểm O(0; 0) bằng 0 và nhỏ hơn 4.
Thay x = -1, y = 3 vào biểu thức 2x – y ta được: 2.(-1) – 3 = - 5 < 4.
Suy ra giá trị biểu thức 2x – y tại điểm A(-1; 3) bằng -5 và nhỏ hơn 4.
Thay x = -2, y = -2 vào biểu thức 2x – y ta được: 2.(-2) – (-2) = -2 < 4.
Suy ra giá trị biểu thức 2x – y tại điểm B(-2; 2) bằng -2 và nhỏ hơn 4.
b) Các điểm C(3; 1), D(4; - 1) cùng thuộc một nửa mặt phẳng bờ là đường thẳng d.
Thay x = 3, y = 1 vào biểu thức 2x – y ta được: 2.3 – 1 = 5 > 4.
Suy ra giá trị biểu thức 2x – y tại điểm C(3; 1) bằng 5 và lớn hơn 4.
Thay x = 4, y = -1 vào biểu thức 2x – y ta được: 2.4 – (-1) = 9 > 4.
Suy ra giá trị biểu thức 2x – y tại điểm A(4; -1) bằng 9 và lớn hơn 4.
Lời giải bài tập Toán 10 Bài 3: Bất phương trình bậc nhất hai ẩn hay, chi tiết khác:
Luyện tập 2 trang 24 Toán 10 Tập 1: Biểu diễn miền nghiệm của bất phương trình 2x + y < 200 trên mặt phẳng tọa độ.
Lời giải:
Bước 1: Vẽ đường thẳng d: 2x + y – 200 = 0 trên mặt phẳng tọa độ.
Bước 2: Lấy điểm M(100; 200) không thuộc đường thẳng d.
Thay x = 100, y = 200 vào 2x + y ta được: 2.100 + 200 = 400 > 200.
Do đó miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là đường thẳng d không chứa điểm M (miền tô màu không chứa đường thẳng d).
Lời giải bài tập Toán 10 Bài 3: Bất phương trình bậc nhất hai ẩn hay, chi tiết khác:
Vận dụng trang 25 Toán 10 Tập 1: Một công ty viễn thông tính phí 1 nghìn đồng mỗi phút gọi nội mạng và 2 nghìn đồng mỗi phút gọi ngoại mạng. Em có thể sử dụng bao nhiêu phút gọi nội mạng và bao nhiêu phút gọi ngoại mạng trong một tháng nếu em muốn số tiền phải trả ít hơn 200 nghìn đồng?
Lời giải:
Gọi số phút gọi nội mạng trọng một tháng là x (phút) và số phút gọi ngoại mạng trong một tháng là y (phút) (x, y ≥ 0)
Số tiền trả cho x phút gọi nội mạng trong một tháng là x (nghìn đồng)
Số tiền trả cho y phút gọi ngoại mạng trong một tháng là 2y (nghìn đồng)
Tổng số tiền phải trả là: x + 2y (nghìn đồng)
Để số tiền cước điện thoại trong một tháng ít hơn 200 nghìn đồng ta có: x + 2y < 200.
Miền nghiệm của bất phương trình bậc nhất hai ẩn này được xác định như sau:
Vẽ đường thẳng d: x + 2y = 200.
Ta lấy gốc tọa độ O(0; 0) và tính 0 + 2.0 = 0 < 200.
Do đó miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là đường thẳng d có chứa gốc tọa độ không kể đường thẳng d.
Vậy nếu dùng x phút gọi nội mạng và y phút gọi ngoại mạng mà điểm (x; y) nằm trong miền tô màu không chứa đường thẳng d thì số tiền phải trả ít hơn 200 nghìn đồng.
Ta thấy bất phương trình trên có vô số nghiệm, vì thế có rất nhiều phương án sử dụng số phút gọi nội mạng và ngoại mạng trong một tháng để số tiền phải trả ít hơn 200 nghìn đồng.
Chẳng hạn xét cặp số (x; y) = (100; 40). Ta có: 100 + 2 . 40 = 180 < 200.
Do đó, cặp số (100; 40) thỏa mãn bất phương trình x + 2y < 200.
Vậy có thể gọi 100 phút gọi nội mạng và 40 phút gọi ngoại mạng để số tiền phải trả trong một tháng ít hơn 200 nghìn đồng.
Tương tự, có thể lấy nhiều ví dụ khác.
Lời giải bài tập Toán 10 Bài 3: Bất phương trình bậc nhất hai ẩn hay, chi tiết khác:
Bài 2.1 trang 25 Toán 10 Tập 1: Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
a) 2x + 3y > 6;
b) 22x + y ≤ 0;
c) 2x2 – y ≥ 1.
Lời giải:
Bất phương trình bậc nhất hai ẩn x,y có dạng tổng quát là: ax + by > c ( ax + by < c, ax + by ≥ 0, ax + by ≤ 0)
Trong đó a, b, c là số thực đã cho, a và b không đồng thời bằng 0, x và y là các ẩn số.
Do đó:
a) 2x + 3y > 6 là bất phương trình bậc nhất hai ẩn với a = 2, b = 3 và c = 6;
b) 22x + y ≤ 0 là bất phương trình bậc nhất hai ẩn với a = 22 = 4, b = 1 và c = 0.
c) 2x2 – y ≥ 1 không là bất phương trình bậc nhất hai ẩn do ẩn x có bậc là 2.
Lời giải bài tập Toán 10 Bài 3: Bất phương trình bậc nhất hai ẩn hay, chi tiết khác:
Bài 2.2 trang 25 Toán 10 Tập 1: Biểu diễn miền nghiệm của mỗi bất phương trình sau trên mặt phẳng tọa độ:
a) 3x + 2y ≥ 300;
b) 7x + 20y < 0.
Lời giải:
a)
Vẽ đường thẳng d: 3x + 2y – 300 = 0 trên mặt phẳng tọa độ.
Lấy gốc tọa độ O(0; 0) và tính 3.0 + 2.0 = 0 < 300.
Do đó miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là đường thẳng d không chứa gốc tọa độ và cả đường thẳng d (miền tô màu kể cả biên).
b)
Vẽ đường thẳng d’: 7x + 20y = 0 trên mặt phẳng tọa độ.
Lấy điểm M(200; 200) và tính 7.200 + 20.200 = 5 400 > 0.
Do đó miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là đường thẳng d’ không chứa điểm M và không chứa đường thẳng d’ (miền tô màu không kể biên).
Lời giải bài tập Toán 10 Bài 3: Bất phương trình bậc nhất hai ẩn hay, chi tiết khác:
Bài 2.3 trang 25 Toán 10 Tập 1: Ông An muốn thuê một chiếc ô tô (có lái xe) trong một tuần. Giá thuê xe được cho như bảng sau:
a) Gọi x và y lần lượt là số kilômét ông An đi trong các ngày từ thứ Hai đến thứ Sáu và trong hai ngày cuối tuần. Viết bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền ông An phải trả không quá 14 triệu đồng.
b) Biểu diễn miền nghiệm của bất phương trình ở câu a trên mặt phẳng tọa độ.
Lời giải:
a) Số tiền ông An phải trả cho việc thuê xe ô tô từ thứ Hai đến thứ Sáu là:
900.5 + 8x = 4 500 + 8x (nghìn đồng).
Số tiền ông An phải trả cho việc thuê xe ô tô trong hai ngày cuối tuần:
1 500.2 + 10y = 3 000 + 10y (nghìn đồng).
Tổng số tiền ông An phải trả cho việc thuê xe trong một tuần là:
4 500 + 8x + 3 000 + 10y = 7 500 + 8x + 10y (nghìn đồng).
Để tổng số tiền ông An phải trả không quá 14 triệu đồng thì
7 500 + 8x + 10y ≤ 14 000
⇔ 8x + 10y ≤ 6 500.
⇔ 4x + 5y ≤ 3 250.
Vậy bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền ông An phải trả không quá 14 triệu đồng là 4x + 5y ≤ 3 250.
b)
Vẽ đường thẳng d: 4x + 5y = 3 250 trên mặt phẳng tọa độ.
Lấy gốc tọa độ O(0; 0) và tính 4.0 + 5.0 = 0 < 3 250.
Do đó miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là đường thẳng d chứa gốc tọa độ và cả đường thẳng d (miền không tô màu kể cả biên).
Lời giải bài tập Toán 10 Bài 3: Bất phương trình bậc nhất hai ẩn hay, chi tiết khác:
Với giải sách bài tập Toán 10 Bài 3: Bất phương trình bậc nhất hai ẩn sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 Bài 3.
Với tóm tắt lý thuyết Toán 10 Bài 3: Bất phương trình bậc nhất hai ẩn sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.
1. Bất phương trình bậc nhất hai ẩn
- Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là:
ax + by ≤ c(ax + by ≥ c, ax + by < c, ax + by > c)
Trong đó a, b, c là những số thực đã cho, a và b không đồng thời bằng 0, x và y là các ẩn số.
- Cặp số (x0; y0)được gọi là một nghiệm của bất phương trình bậc nhất hai ẩn ax + by ≤ cnếu bất đẳng thức ax0 + by0 ≤ cđúng.
Nhận xét: Bất phương trình bậc nhất hai ẩn luôn có vô số nghiệm.
Ví dụ:
5x + 2y < 4 là bất phương trình bậc nhất hai ẩn.
5x + 2y – 3z > 3không là bất phương trình bậc nhất hai ẩn.
Ví dụ về nghiệm của bất phương trình 5x + 2y < 4:
Vì 5.(–1) + 2(–2) = –9 < 4 nên cặp số (–1; –2) là nghiệm của bất phương trình.
Vì 5.0 + 2.0 = 0 < 4 nên cặp số (0; 0) là nghiệm của bất phương trình.
Vì 5.(–1) + 2.2 = –1 < 4 nên cặp số (–1;2) là nghiệm của bất phương trình.
Ta có thể tìm thêm được nhiều cặp số thỏa mãn bất phương trình đã cho. Do đó bất phương trình bậc nhất hai ẩn 5x + 2y < 4 có các cặp nghiệm là (–1; –2); (0; 0); (–1; 2) … hay bất phương trình này có vô số nghiệm.
2. Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ
- Trong mặt phẳng tọa độ Oxy, tập hợp các điểm có tọa độ là nghiệm của bất phương trình ax + by ≤ c được gọi là miền nghiệm của bất phương trình đó.
- Người ta chứng minh được rằng đường thẳng d có phương trình ax + by = c chia mặt phẳng tọa độ Oxy thành 2 nửa mặt phẳng bờ d:
+ Một nửa mặt phẳng (không kể bờ d) gồm các điểm có tọa độ thỏa mãn ax + by > c;
+ Một nửa mặt phẳng (không kể bờ d) gồm các điểm có tọa độ thỏa mãn ax + by < c;
Bờ d gồm các điểm có tọa độ (x; y) thỏa mãn ax + by = c.
- Cách biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn ax + by ≤ c:
+ Vẽ đường thẳng d: ax + by = c trên mặt phẳng tọa độ Oxy.
+ Lấy một điểm M0(x0; y0) không thuộc d.
+ Tính ax0 + by0 và so sánh với c.
+ Nếu ax0 + by0 < c thì nửa mặt phẳng bờ d chứa M0 là miền nghiệm của bất phương trình. Nếu ax0 + by0 > c thì nửa mặt phẳng bờ d không chứa M0 là miền nghiệm của bất phương trình.
Chú ý: Miền nghiệm của bất phương trình ax + by < c là miền nghiệm của bất phương trình ax + by ≤ c bỏ đi đường thẳng ax + by = c và biểu diễn đường thẳng bằng nét đứt.
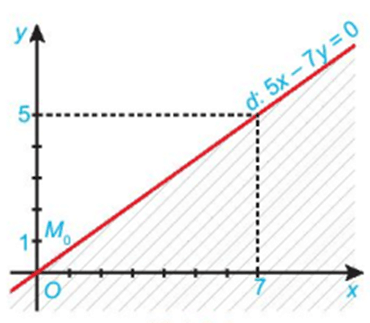
Ví dụ: Biểu diễn miền nghiệm của bất phương trình 5x – 7y ≤ 0 trên mặt phẳng tọa độ:
Bước 1: Vẽ đường thẳng d: 5x – 7y = 0 trên mặt phẳng tọa độ Oxy.
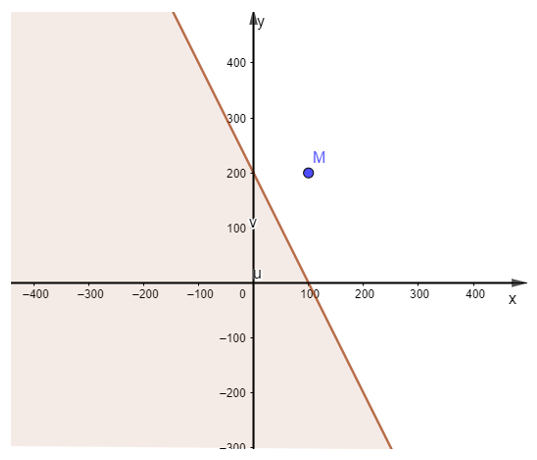
Bước 2: Lấy điểm M0(0; 1) không thuộc d và thay x = 0 và y = 1 vào biểu thức 5x – 7y ta được 5.0 – 7.1 = –7 < 0 là mệnh đề đúng.
Do đó miền nghiệm của bất phương trình là nửa mặt phẳng bờ d chứa điểm M0 (miền không bị gạch)
Bài 1. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
a) 2x + 5y < 7
b) 2x2 + y > 8
c) 3y2 < 4
d) 4x – 5 < 3y
e) 4x + 5y – 6t < 3
Hướng dẫn giải
Các bất phương trình là bất phương trình bậc nhất hai ẩn:
Ta có: 2x + 5y < 7 có dạng ax + by < c với a = 2, b = 5 và c = 7. Do đó a) là bất phương trình bậc nhất hai ẩn.
Ta có: 2x2 + y > 8 là bất phương trình bậc hai nên b) không là bất phương trình bậc nhất hai ẩn.
Ta có: y2 < 4 là bất phương trình bậc hai nên c) không là bất phương trình bậc nhất hai ẩn.
Ta có 4x – 5 < 3y ⇔ 4x – 3y < 5 có dạng ax + by < c với a = 4, b = – 3 và c = 5. Do đó d) là bất phương trình bậc nhất hai ẩn.
Ta có 4x + 5y – 6t < 3 là bất phương trình bậc nhất ba ẩn x, y, t. Do đó e) không là bất phương trình bậc nhất hai ẩn.
Vậy 2x + 5y < 7; 4x – 5 < 3y là các bất phương trình bậc nhất hai ẩn.
Bài 2. Bất phương trình sau có phải là bất phương trình bậc nhất hai ẩn không? Nếu có biểu diễn miền nghiệm của nó trên trục tọa độ Oxy: x + y ≥ 100?
Hướng dẫn giải
Bất phương trình x + y ≥ 100 là bất phương trình bậc nhất hai ẩn.
- Biểu diễn miền nghiệm trên trục tọa độ Oxy:
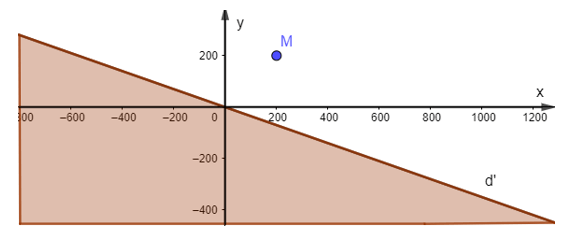
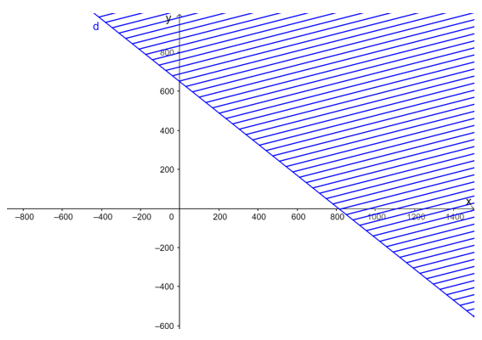
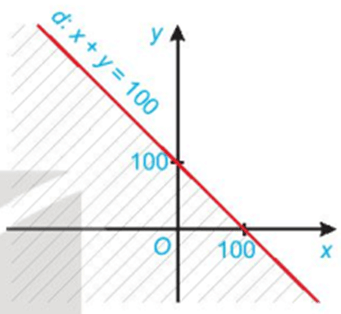
+ Vẽ đường thẳng d: x + y = 100 trên mặt phẳng tọa độ Oxy.
+ Lấy điểm O(0; 0) thay vào bất phương trình ta có: 0 + 0 ≥ 100 là một mệnh đề sai.
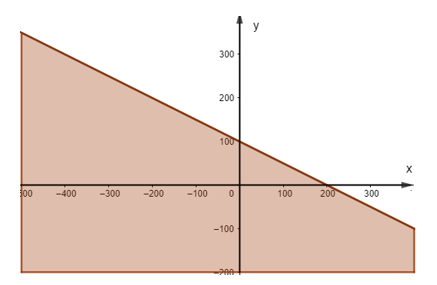
Vậy miền nghiệm của bất phương trình đã cho trên trục tọa độ Oxy là nửa mặt phẳng bờ d không chứa gốc tọa độ O.
Miền nghiệm biểu diễn trên trục tọa độ Oxy:
Bài 3. Cho bất phương trình bậc nhất hai ẩn: x + y < 20 . Cặp nghiệm nào sau đây là nghiệm của bất phương trình trên?
(x; y) = (2; 5), (4; 8), (5; 6), (4; 7), (11; 12).
Hướng dẫn giải
Thay (x; y) = (2; 5) vào bất phương trình ta có: 2 + 5 = 7 < 20 (luôn đúng). Do đó cặp số (2;5) là nghiệm của bất phương trình đã cho.
Thay (x; y) = (4; 8) vào bất phương trình ta có: 4 + 8 = 12 < 20 (luôn đúng). Do đó cặp số (4;8) là nghiệm của bất phương trình đã cho.
Thay (x; y) = (5; 6) vào bất phương trình ta có: 5 + 6 = 11 < 20 (luôn đúng). Do đó cặp số (5;6) là nghiệm của bất phương trình đã cho.
Thay (x; y) = (4; 7) vào bất phương trình ta có: 4 + 7 = 11 < 20 (luôn đúng). Do đó cặp số (4;7) là nghiệm của bất phương trình đã cho.
Thay (x; y) = (11; 12) vào bất phương trình ta có: 11 + 12 = 23 < 20 (sai). Do đó cặp số (11;12) không là nghiệm của bất phương trình đã cho.
Vậy ta có cặp nghiệm thỏa mãn là:
(x; y) = (2; 5), (4; 8), (5; 6), (4; 7).
Bài 4. Cho bất phương trình bậc nhất hai ẩn: 4x + y ≤ 15.
a) Chỉ ra 2 nghiệm của bất phương trình trên.
b) Với x = 0 thì có bao nhiêu giá trị của y thỏa mãn bất phương trình.
Hướng dẫn giải
a) Chọn (x; y) = (0; 0)
Thay x = 0 và y = 0 vào bất phương trình đã cho ta được 4.0 + 0 ≤ 15 là mệnh đề đúng. Do đó cặp (0; 0) là nghiệm của bất phương trình.
Chọn (x; y) = (0; 1)
Thay x = 0 và y = 1 vào bất phương trình đã cho ta được 4.0 + 1 ≤ 15 là mệnh đề đúng. Do đó cặp (0; 1) là nghiệm của bất phương trình.
Vậy hai cặp nghiệm của bất phương trình: (x; y) = (0; 0), (0; 1).
b) Với x = 0 thì bất phương trình trở thành: y ≤ 15 và có vô số giá trị của y thỏa mãn bất phương trình.
Các bài học để học tốt Bất phương trình bậc nhất hai ẩn Toán lớp 10 hay khác:
Với 15 bài tập trắc nghiệm Bất phương trình bậc nhất hai ẩn Toán lớp 10 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.
Câu 1. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
A. x2 + y > 0;
B. x2 + 3y2 = 2;
C. –x + y3 ≤ 0;
D. x – y < 1.
Câu 2. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
A. x2 < 3x – 7y;
B. x + 3y2 ≥0;
C. –22x + y ≤4;
D. 0x – 0y ≤ 5.
Câu 3. Bất phương trình nào tương đương với bất phương trình 3x – y > 7(x – 4y) + 1?
A. 4x – 27y + 1 > 0;
B. 4x – 27y + 1 ≥ 0;
C. 4x – 27y < –1;
D. 4x – 27y + 1 ≤ 0.
Câu 4. Cho bất phương trình x + y ≤ 2 (1). Chọn khẳng định đúng trong các khẳng định sau:
A. Bất phương trình (1) chỉ có một nghiệm duy nhất;
B. Bất phương trình (1) chỉ có hai nghiệm;
C. Bất phương trình (1) luôn có vô số nghiệm;
D. Bất phương trình (1) vô nghiệm.
Câu 5. Miền nghiệm của bất phương trình: –3x + y > 0 chứa điểm nào trong các điểm sau:
A. (–3; 0);
B. (3; 2);
C. (0; 0);
D. (1; 1);
Câu 6. Bạn Lan để dành được 300 nghìn đồng. Trong một đợt ủng hộ học sinh khó khăn, bạn Lan đã ủng hộ x tờ tiền loại 10 nghìn đồng, y tờ tiền loại 20 nghìn đồng từ tiền để dành của mình. Trong các bất phương trình sau, bất phương trình nào diễn tả giới hạn về tổng số tiền mà bạn Lan đã ủng hộ.
A. x + y < 300 ;
B. 10x + y < 300 ;
C. 10x + 20y > 300;
D. 10x + 20y ≤ 300.
Câu 7. Miền nghiệm của bất phương trình 4x + 3y ≤ 1 là:
A. Đường thẳng d: 4x + 3y = 1;
B. Đường thẳng d: 4x + 3y = 1 và điểm O(0;0);
C. Nửa mặt phẳng bờ là đường thẳng d: 4x + 3y = 1 không chứa điểm O(0;0) (kể cả bờ d);
D. Nửa mặt phẳng bờ là đường thẳng d: 4x + 3y = 1 chứa điểm O(0; 0) (kể cả bờ d).
Câu 8. Điểm nào trong các điểm sau thuộc miền nghiệm của bất phương trình: 2(x + 3) – 4(y –1) < 0.
A. (0; 0);
B. (1; 0);
C. (0; 1);
D. (–5; 1).
Câu 9. Cặp số nào sau đây không là nghiệm của bất phương trình: x – 4y ≥ –5.
A. (–5; 0);
B. (0; 0);
C. (–2; 1);
D. (1; –3).
Câu 10. Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình:
4(2 – y) > 2x + y – 2.
A. (0; 0);
B. (1; 0);
C. ( 1; 2);
D. ( –1; 1).
Câu 11. Điểm A(1; –3) là điểm thuộc miền nghiệm của bất phương trình nào?
A. –3x + 2y –3 > 0;
B. 3x – y ≤ 0;
C. 3x – y > 0;
D. y – 2x > – 4.
Câu 12. Cặp số (2 ; 3) là nghiệm của bất phương trình nào sau đây?
A. –2x + 3y < –1;
B. x + y ≤ 0;
C. 4x ≥ 2y + 1;
D. x – y + 6 < 0.
Câu 13. Miền nghiệm của bất phương trình x + y < 1 là miền không bị gạch trong hình vẽ nào sau đây?
A.
B.
C.
D.
Câu 14. Miền không gạch trong hình vẽ sau (bao gồm cả bờ), biểu diễn tập nghiệm của bất phương trình nào trong các bất phương trình sau?
A. –2x + y > 2;
B. –2x + y < 2;
C. –2x + y ≤ 2;
D. –2x + y ≥ 2.
Câu 15. Cho hai bất phương trình 2x + y < 3 (1) và – x + 3y > 5 (2) và điểm A(0; 1). Kết luận nào sau đây là đúng?
A. Điểm A thuộc miền nghiệm của bất phương trình (1) và (2);
B. Điểm A thuộc miền nghiệm của bất phương trình (1) nhưng không thuộc miền nghiệm của (2);
C. Điểm A không thuộc miền nghiệm của bất phương trình (1) nhưng thuộc miền nghiệm của (2);
D. Điểm A không thuộc miền nghiệm của cả hai bất phương trình (1) và (2).
Xem thêm bài tập trắc nghiệm Toán lớp 10 Kết nối tri thức có đáp án hay khác: