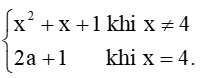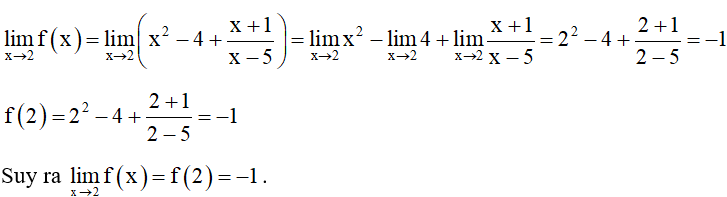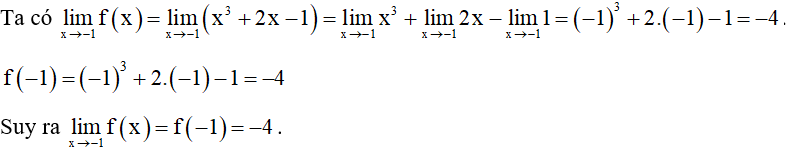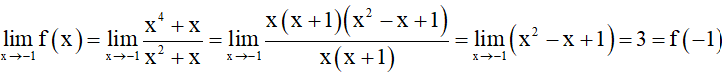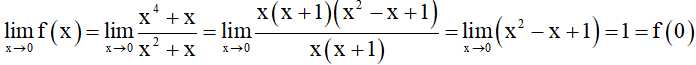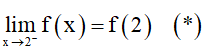Với giải bài tập Toán 11 Bài 3: Hàm số liên tục sách Cánh diều hay nhất, chi tiết giúp học sinh lớp 11 dễ dàng làm bài tập Toán 11 Bài 3.

Giải Toán 11 Cánh diều Bài 3: Hàm số liên tục

Giải Toán 11 trang 73

Câu hỏi khởi động trang 73 Toán 11 Tập 1 Cánh diều

Giải Toán 11 Bài 3: Hàm số liên tục - Cánh diều

Câu hỏi khởi động trang 73 Toán 11 Tập 1: Cầu sông Hàn là một trong những cây cầu bắc qua sông Hàn ở Đà Nẵng. Đây là cây cầu đầu tiên do kĩ sư, công nhân Việt Nam tự thiết kế và thi công. Khi cầu không quay (Hình 10a), mặt cầu liền mạch nên các phương tiện có thể đi lại giữa hai đầu cầu. Khi cầu quay (Hình 10b) để các tàu, thuyền có thể đi qua thì mặt cầu không còn liền mạch nữa, các phương tiện không thể đi qua giữa hai đầu cầu.

Kiến thức gì trong toán học thể hiện chuyển động có đường đi là đường liền mạch?

Lời giải:

Kiến thức trong toán học thể hiện chuyển động của đường đi là đường liên mạch đó là kiến thức về hàm số liên tục.

Để tìm hiểu kĩ hơn hàm số liên tục là gì thì chúng ta sẽ cùng tìm hiểu bài học ngày hôm nay. Bài học: “Hàm số liên tục”.

Lời giải bài tập Toán 11 Bài 3: Hàm số liên tục hay, chi tiết khác:

Hoạt động 1 trang 73 Toán 11 Tập 1 Cánh diều

Giải Toán 11 Bài 3: Hàm số liên tục - Cánh diều

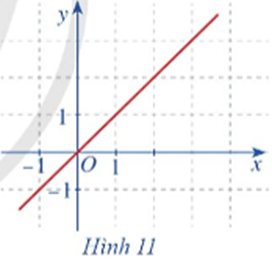
Hoạt động 1 trang 73 Toán 11 Tập 1: Quan sát đồ thị hàm số f(x) = x ở Hình 11.

a) Tính $\underset{x\to 1}{\lim }$f(x).

b) So sánh $\underset{x\to 1}{\lim }$f(x)và f(1).

Lời giải:

a) Ta có: $\underset{x\to 1}{\lim }f\left(x\right)=\underset{x\to 1}{\lim }x$ = 1.

b) Ta có: f(1) = 1 nên $\underset{x\to 1}{\lim }$f(x)=f(1).

Lời giải bài tập Toán 11 Bài 3: Hàm số liên tục hay, chi tiết khác:

Luyện tập 1 trang 74 Toán 11 Tập 1 Cánh diều

Giải Toán 11 Bài 3: Hàm số liên tục - Cánh diều

Luyện tập 1 trang 74 Toán 11 Tập 1: Xét tính liên tục của hàm số f(x) = x³ + 1 tại x₀ = 1.

Lời giải:

Ta có: $\underset{x\to 1}{\lim }f\left(x\right)=\underset{x\to 1}{\lim }\left(x^3+1\right)$ = 2và f(1) = 1³ + 1 = 2

Suy ra $\underset{x\to 1}{\lim }$f(x)=f(1).

Vì vậy hàm số liên tục tại x₀ = 1.

Lời giải bài tập Toán 11 Bài 3: Hàm số liên tục hay, chi tiết khác:

Hoạt động 2 trang 74 Toán 11 Tập 1 Cánh diều

Giải Toán 11 Bài 3: Hàm số liên tục - Cánh diều

Hoạt động 2 trang 74 Toán 11 Tập 1: Cho hàm số f(x) = x + 1 với x ∈ ℝ.

a) Giả sử x₀ ∈ ℝ. Hàm= số f(x) có liên tục tại điểm x₀ hay không?

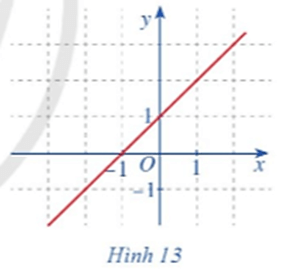
b) Quan sát đồ thị hàm số f(x) = x + 1 với x ∈ ℝ (Hình 13), nêu nhận xét về đặc điểm của đồ thị hàm số đó.

Lời giải:

a) Với x₀ ∈ ℝ bất kì ta có: $\underset{x\to x_0}{\lim }$f(x) = x_o+1 - f(x_o). Do đó hàm số liên tục tại x = x₀.

b) Dựa vào đồ thị hàm số ta thấy: Đồ thị hàm số là một đường thẳng liền mạch với mọi giá trị x ∈ ℝ.

Lời giải bài tập Toán 11 Bài 3: Hàm số liên tục hay, chi tiết khác:

Luyện tập 2 trang 75 Toán 11 Tập 1 Cánh diều

Giải Toán 11 Bài 3: Hàm số liên tục - Cánh diều

Luyện tập 2 trang 75 Toán 11 Tập 1: Hàm số f(x) = 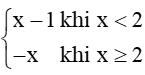. Có liên tục trên ℝ hay không?

Lời giải:

+) Với mỗi x₀ ∈ (– ∞; 2) có $\underset{x\to x_0}{\lim }f\left(x\right)=\underset{x\to x_0}{\lim }\left(x-1\right)=x_0-1=f\left(x_0\right)$là hàm số liên tục.

+) Với mỗi x₀ ∈ (2; +∞) có $\underset{x\to x_0}{\lim }f\left(x\right)=\underset{x\to x_0}{\lim }\left(-x\right)=-x_0=f\left(x_0\right)$là hàm số liên tục.

+) Tại x = 2, ta có: $\underset{x\to 2}{\lim }f\left(x\right)=\underset{x\to 2}{\lim }$(x-1) = 1và f(2) = – 2 nên $\underset{x\to 2}{\lim }f\left(x\right)\ne f\left(2\right)$.

Vậy hàm số không liên tục tại x = 2.

Lời giải bài tập Toán 11 Bài 3: Hàm số liên tục hay, chi tiết khác:

Hoạt động 3 trang 75 Toán 11 Tập 1 Cánh diều

Giải Toán 11 Bài 3: Hàm số liên tục - Cánh diều

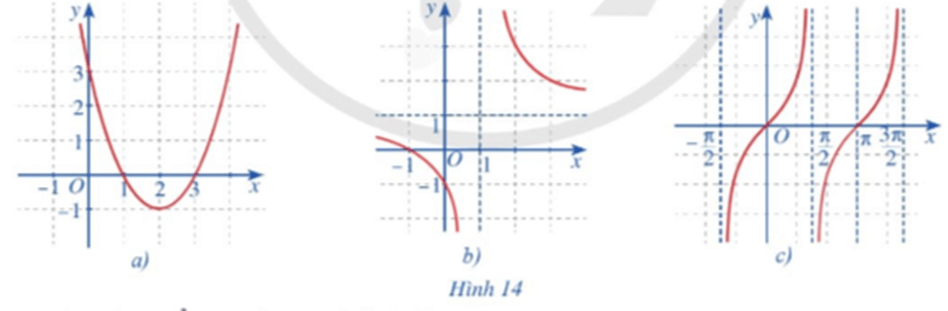
Hoạt động 3 trang 75 Toán 11 Tập 1: Quan sát đồ thị các hàm số: y = x² – 4x + 3 (Hình 14a); y = $\frac{x+1}{x-1}\left(x\ne 1\right)$(Hình 14b); y = tanx (Hình 14c) và nêu nhận xét về tính liên tục của mỗi hàm số đó trên từng khoảng của tập xác định.

Lời giải:

Hình 14a) đồ thị là đường cong Parabol liền mạch nên hàm số liên tục trên toàn bộ khoảng xác định.

Hình 14b) đồ thị bị chia làm hai nhánh:

- Với x < 1 ta thấy hàm số là một đường cong liền nên liên tục.

- Với x > 1 ta thấy hàm số là một đường cong liền nên liên tục.

Vậy hàm đố liên tục trên từng khoảng xác định.

Hình 14c) đồ thị hàm số y = tanx chia thành nhiều nhánh, và mỗi nhánh là các đường cong liền. Do đó hàm số liên tục trên mỗi khoảng xác định của chúng.

Lời giải bài tập Toán 11 Bài 3: Hàm số liên tục hay, chi tiết khác:

Luyện tập 3 trang 76 Toán 11 Tập 1 Cánh diều

Giải Toán 11 Bài 3: Hàm số liên tục - Cánh diều

Luyện tập 3 trang 76 Toán 11 Tập 1: Hàm f(x)=$\frac{x+2}{x-8}$có liên tục trên mỗi khoảng (– ∞; 8), (8; + ∞) hay không?

Lời giải:

Do f(x)=$\frac{x+2}{x-8}$nên hàm số liên tục trên mỗi khoảng (– ∞; 8), (8; + ∞).

Lời giải bài tập Toán 11 Bài 3: Hàm số liên tục hay, chi tiết khác:

Hoạt động 4 trang 76 Toán 11 Tập 1 Cánh diều

Giải Toán 11 Bài 3: Hàm số liên tục - Cánh diều

Hoạt động 4 trang 76 Toán 11 Tập 1: Cho hai hàm số f(x)= x³ + x và g(x) = x² + 1 (x ∈ ℝ). Hãy cho biết:

a) Hai hàm số f(x), g(x) có liên tục tại x = 2 hay không.

b) Các hàm số f(x) + g(x); f(x) – g(x); f(x).g(x); $\frac{f\left(x\right)}{g\left(x\right)}$có liên tục tại x = 2 hay không.

Lời giải:

a) Tại x = 2 có $\underset{x\to 2}{\lim }f\left(x\right)=\underset{x\to 2}{\lim }\left(x^3+x\right)$ = 2³+2 = 10 = f(2). Do đó hàm số f(x) liên tục tại x = 2.

Tại x = 2 có $\underset{x\to 2}{\lim }g\left(x\right)=\underset{x\to 2}{\lim }\left(x^2+1\right)$ = 2²+1 = 5 = g(2). Do đó hàm số g(x) liên tục tại x = 2.

b) Tại x = 2 có$\underset{x\to 2}{\lim }\left(f\left(x\right)+g\left(x\right)\right)=\underset{x\to 2}{\lim }f\left(x\right)+\underset{x\to 2}{\lim }f\left(x\right)=10+5=15=f\left(2\right)+g\left(2\right)$

Do đó hàm số f(x) + g(x) liên tục tại x = 2.

Tại x = 2 có $\underset{x\to 2}{\lim }\left(f\left(x\right)-g\left(x\right)\right)=\underset{x\to 2}{\lim }f\left(x\right)-\underset{x\to 2}{\lim }g\left(x\right)=10-5=5=f\left(2\right)-g\left(2\right)$

Do đó hàm số f(x) – g(x) liên tục tại x = 2.

Tại x = 2 có $\underset{x\to 2}{\lim }\left(f\left(x\right).g\left(x\right)\right)=\underset{x\to 2}{\lim }f\left(x\right).\underset{x\to 2}{\lim }g\left(x\right)=10.5=50=f\left(2\right).g\left(2\right)$

Do đó hàm số f(x).g(x) liên tục tại x = 2.

Tại x = 2 có $\underset{x\to 2}{\lim }\left(\frac{f\left(x\right)}{g\left(x\right)}\right)=\frac{\underset{x\to 2}{\lim }f\left(x\right)}{\underset{x\to 2}{\lim }g\left(x\right)}=\frac{10}{5}=2=\frac{f\left(2\right)}{g\left(2\right)}$

Do đó hàm số $\frac{f\left(x\right)}{g\left(x\right)}$ liên tục tại x = 2.

Lời giải bài tập Toán 11 Bài 3: Hàm số liên tục hay, chi tiết khác:

Luyện tập 4 trang 76 Toán 11 Tập 1 Cánh diều

Giải Toán 11 Bài 3: Hàm số liên tục - Cánh diều

Luyện tập 4 trang 76 Toán 11 Tập 1: Xét tính liên tục của hàm số f(x) = sinx + cosx trên ℝ.

Lời giải:

Hàm số sinx và cosx liên tục trên ℝ.

Do đó hàm số y = sinx + cosx liên tục trên ℝ.

Lời giải bài tập Toán 11 Bài 3: Hàm số liên tục hay, chi tiết khác:

Bài 1 trang 77 Toán 11 Tập 1 Cánh diều

Giải Toán 11 Bài 3: Hàm số liên tục - Cánh diều

Bài 1 trang 77 Toán 11 Tập 1: Dùng định nghĩa xét tính liên tục của hàm số f(x) = 2x³ + x + 1 tại điểm x = 2.

Lời giải:

Hàm số f(x) = 2x³ + x + 1 xác định trên ℝ.

Ta có: $\underset{x\to 2}{\lim }f\left(x\right)=\underset{x\to 2}{\lim }\left(2x^3+x+1\right)$ = 2.2³+2+1 = 17 = f(2).

Do đó hàm số liên tục tại x = 2.

Lời giải bài tập Toán 11 Bài 3: Hàm số liên tục hay, chi tiết khác:

Bài 2 trang 77 Toán 11 Tập 1 Cánh diều

Giải Toán 11 Bài 3: Hàm số liên tục - Cánh diều

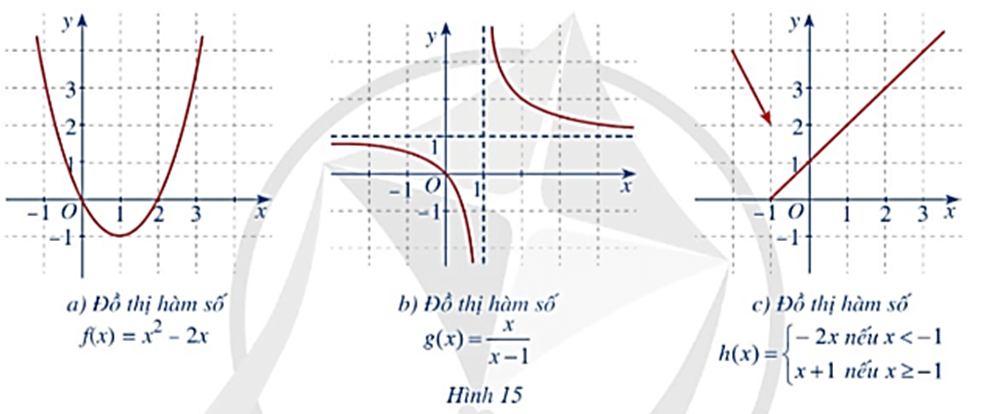
Bài 2 trang 77 Toán 11 Tập 1: Trong các hàm số có đồ thị ở Hình 15a, 15b, 15c, hàm số nào liên tục trên tập xác định của hàm số đó? Giải thích.

Lời giải:

+) Hình 15a): Hàm số f(x) = x² – 2x có tập xác định D = ℝ.

Hàm số liên tục trên toàn bộ ℝ.

+) Hình 16b): Hàm số g(x)= $\frac{x}{x-1}$có tập xác định D = ℝ\{1}.

Do đó hàm số liên tục trên từng khoảng xác định của hàm số.

+) Hình 16c):

Với x ∈ (– ∞; – 1) có f(x) = – 2x liên tục.

Với x ∈ (– 1; ∞) có f(x) = x + 1 liên tục.

Tại x = – 1 có $\underset{x\to -1}{\lim }f\left(x\right)=\underset{x\to -1}{\lim }2x=-2$và f(– 1) = – 1 + 1 = 0.

Suy ra $\underset{x\to -1}{\lim }f\left(x\right)\ne$f(-1). Do đó hàm số liên tục tại x = – 1.

Vậy hàm số kiên tục trên các khoảng (– ∞; – 1) và (– 1; ∞).

Lời giải bài tập Toán 11 Bài 3: Hàm số liên tục hay, chi tiết khác:

Bài 3 trang 77 Toán 11 Tập 1 Cánh diều

Giải Toán 11 Bài 3: Hàm số liên tục - Cánh diều

Bài 3 trang 77 Toán 11 Tập 1: Bạn Nam cho rằng: “Nếu hàm số y = f(x) liên tục tại điểm x₀, còn hàm số y = g(x) không liên tục tại x₀, thì hàm số y = f(x) + g(x) không liên tục tại x₀”. Theo em, ý kiến của bạn Nam đúng hay sai? Giải thích.

Lời giải:

Theo em ý kiến của bạn Nam là đúng.

Ta có: Hàm số y = f(x) liên tục tại điểm x₀ nên $\underset{x\to x_0}{\lim }f\left(x\right)=f\left(x_0\right)$.

Hàm số y = g(x) không liên tục tại x₀ nên $\underset{x\to x_0}{\lim }g\left(x\right)\ne g\left(x_0\right)$.

Do đó $\underset{x\to x_0}{\lim }\left(f\left(x\right)+g\left(x\right)\right)=\underset{x\to x_0}{\lim }f\left(x\right)+\underset{x\to x_0}{\lim }g\left(x\right)\ne f\left(x_0\right)+g\left(x_0\right)$.

Vì vậy hàm số không liên tục tại x₀.

Lời giải bài tập Toán 11 Bài 3: Hàm số liên tục hay, chi tiết khác:

Bài 4 trang 77 Toán 11 Tập 1 Cánh diều

Giải Toán 11 Bài 3: Hàm số liên tục - Cánh diều

Bài 4 trang 77 Toán 11 Tập 1: Xét tính liên tục của mỗi hàm số sau trên tập xác định của hàm số đó:

a) f(x) = x² + sinx;

b) g(x) = x⁴ – x² + $\frac{6}{x-1}$;

c) h(x) = $\frac{2x}{x-3}+\frac{x-1}{x+4}$.

Lời giải:

a) Hàm số f(x) = x² + sinx có tập xác định là ℝ.

Hàm số x² và sinx liên tục trên ℝ nên hàm số f(x) = x² + sinx liên tục trên ℝ.

b) Hàm số g(x) = x⁴ – x² + $\frac{6}{x-1}$có tập xác định là ℝ\{1}.

Hàm số x⁴ – x² liên tục trên toàn bộ tập xác định

Hàm số $\frac{6}{x-1}$liên tục trên các khoảng ( – ∞; 1) và (1; +∞).

Vậy hàm số đã cho liên tục trên từng khoảng xác định của hàm số.

c) Hàm số h(x) = $\frac{2x}{x-3}+\frac{x-1}{x+4}$có tập xác định D = ℝ\{– 4; 3}.

Hàm số $\frac{2x}{x-3}$ liên tục trên các khoảng ( – ∞; 3) và (3; +∞).

Hàm số $\frac{x-1}{x+4}$ liên tục trên các khoảng ( – ∞; – 4) và (– 4; +∞).

Lời giải bài tập Toán 11 Bài 3: Hàm số liên tục hay, chi tiết khác:

Bài 5 trang 77 Toán 11 Tập 1 Cánh diều

Giải Toán 11 Bài 3: Hàm số liên tục - Cánh diều

Bài 5 trang 77 Toán 11 Tập 1: Cho hàm số f(x) =

a) Với a = 0, xét tính liên tục của hàm số tại x = 4.

b) Với giá trị nào của a thì hàm số liên tục tại x = 4?

c) Với giá trị nào của a thì hàm số liên tục trên tập xác định của nó?

Lời giải:

a) Với a = 0, tại x = 4, ta có:

$\underset{x\to 4}{\lim }f\left(x\right)=\underset{x\to 4}{\lim }\left(x^2+x+1\right)=4^2$+4+1 = 21 và f(4) = 2.0 + 1 = 1

Suy ra $\underset{x\to 4}{\lim }f\left(x\right)\ne f\left(4\right)$.

Vì vậy hàm số không liên tục tại x = 4.

b) Ta có: $\underset{x\to 4}{\lim }f\left(x\right)=\underset{x\to 4}{\lim }\left(x^2+x+1\right)=4^2$+4+1 = 21và f(4) = 2.a + 1

Để hàm số liên tục tại x = 4 thì $\underset{x\to 4}{\lim }$f(x) = f(4)

⇔ 21 = 2a + 1

⇔ 2a = 20

⇔ a = 10

Vậy với a = 10 thì hàm số liên tục tại x = 4.

c) Với x ∈ (– ∞; 4) có f(x) = x² + x + 1 liên tục với mọi x thuộc khoảng này.

Với x ∈ (4; +∞) có f(x) = 2a + 1 liên tục với mọi x thuộc khoảng này.

Tại x = 4 thì a = 10 hàm số liên tục.

Vậy với a = 10 hàm số liên tục trên tập xác định của nó.

Lời giải bài tập Toán 11 Bài 3: Hàm số liên tục hay, chi tiết khác:

Bài 6 trang 77 Toán 11 Tập 1 Cánh diều

Giải Toán 11 Bài 3: Hàm số liên tục - Cánh diều

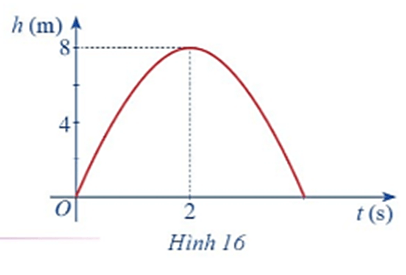
Bài 6 trang 77 Toán 11 Tập 1: Hình 16 biểu thị độ cao h(m) của một quả bóng đá lên theo thời gian t(s), trong đó h(t) = – 2t² + 8t.

a) Chứng tỏ hàm số h(t) liên tục trên tập xác định.

b) Dựa vào đồ thị hãy xác định $\underset{t\to 2}{\lim }\left(-2t^2+8t\right)$.

Lời giải:

a) Hàm số h(t) = – 2t² + 8t là hàm đa thức nên liên tục trên tập xác định.

b) Dựa vào đồ thị hàm số khi t tiến dần đế 2 thì h(t) dần đến 8.

Vậy $\underset{t\to 2}{\lim }\left(-2t^2+8t\right)=8$.

Lời giải bài tập Toán 11 Bài 3: Hàm số liên tục hay, chi tiết khác:

SBT Toán 11 Cánh diều Bài 3: Hàm số liên tục

Với giải sách bài tập Toán 11 Bài 3: Hàm số liên tục sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 11 Bài 3.

Giải SBT Toán 11 Cánh diều Bài 3: Hàm số liên tục

Hàm số liên tục (Lý thuyết Toán lớp 11) | Cánh diều

Với tóm tắt lý thuyết Toán 11 Bài 3: Hàm số liên tục sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 11 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 11.

Hàm số liên tục (Lý thuyết Toán lớp 11) | Cánh diều

Lý thuyết Hàm số liên tục

1. Khái niệm

1.1. Hàm số liên tục tại một điểm

Cho hàm số y = f(x) xác định trên khoảng (a; b) và x₀ ∈ (a; b). Hàm số y = f(x) được gọi là liên tục tại x₀ nếu .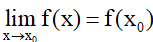

Nhận xét: Hàm số y = f(x) không liên tục tại x₀ được gọi là gián đoạn tại x₀.

Ví dụ 1. Xét tính liên tục của hàm số f(x) = x² + 2 tại x₀ = 1.

Hướng dẫn giải

Ta có: .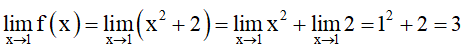

           f(1) = 1² + 2 = 3.

Suy ra .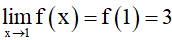

Vậy hàm số f(x) = x² + 2 liên tục tại x₀ = 1.

1.2. Hàm số liên tục trên một khoảng hoặc một đoạn

– Hàm số y = f(x) được gọi là liên tục trên khoảng (a; b) nếu hàm số liên tục tại mọi điểm thuộc khoảng đó.

– Hàm số y = f(x) được gọi là liên tục trên đoạn [a; b] nếu hàm số liên tục trên khoảng (a; b) và .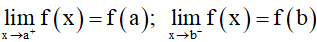

Chú ý: Khái niệm hàm số liên tục trên các tập hợp có dạng (a; b], [a; b), (a; +∞), [a; +∞), (–∞; a), (–∞; a], (–∞;+∞) được định nghĩa tương tự.

Nhận xét: Đồ thị hàm số liên tục trên một khoảng là “đường liền” trên khoảng đó.

Ví dụ 2. Hàm số y = x² + 2x + 1 có liên tục trên đoạn [1; 3] hay không?

Hướng dẫn giải

Với mỗi x₀ ∈ (1; 3), ta có

Ta lại có: .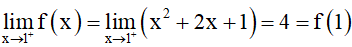

.

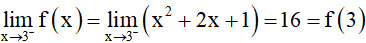
Vậy hàm số đã cho liên tục trên đoạn [1; 3].

2. Một số định lí cơ bản

2.1. Tính liên tục của một số hàm số sơ cấp cơ bản

– Các hàm đa thức và hai hàm số lượng giác y = sinx, y = cosx liên tục trên ℝ.

– Các hàm phân thức hữu tỉ và hai hàm số lượng giác y = tanx, y = cotx liên tục trên từng khoảng xác định của chúng.

– Hàm căn thức $y=\sqrt{x}$ liên tục trên nửa khoảng [0; +∞).

Ví dụ 3. Hàm số 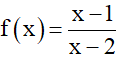 có liên tục trên mỗi khoảng (–∞; 2) và (2; +∞) hay không?

Hướng dẫn giải

Tập xác định của hàm số 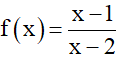 là D = (–∞; 2) ∪ (2; +∞).

Vậy hàm số 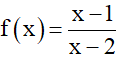 liên tục trên mỗi khoảng (–∞; 2) và (2; +∞).

2. Tính liên tục của tổng, hiệu, tích, thương của hai hàm số liên tục

Giả sử y = f(x) và y = g(x) là hai hàm số liên tục tại điểm x₀. Khi đó:

a) Các hàm số y = f(x) + g(x), y = f(x) – g(x) và y = f(x) . g(x) liên tục tại x₀;

b) Hàm số 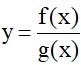 liên tục tại x₀ nếu g(x₀) ≠ 0.

Ví dụ 4. Cho hàm số .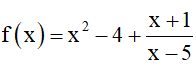

a) Xét tính liên tục của hàm số f(x) tại x = 2.

b) Xét tính liên tục của hàm số f(x) trên tập xác định của hàm số đó.

Hướng dẫn giải

Tập xác định của hàm số là D = ℝ\{5}.

a) Ta có:

Vậy f(x) liên tục tại x = 2.

b) Đặt g(x) = x² – 4; .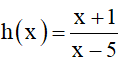

Ta có 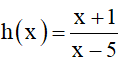 là hàm phân thức hữu tỉ nên liên tục trên mỗi khoảng xác định (–∞; 5) và (5; +∞).

Hàm g(x) = x² – 4 là hàm đa thức nên liên tục trên ℝ. Do đó hàm số g(x) liên tục trên mỗi khoảng (–∞; 5) và (5; +∞).

Vậy hàm số f(x) = g(x) + h(x) liên tục trên mỗi khoảng (–∞; 5) và (5; +∞).

Bài tập Hàm số liên tục

Bài 1. Dùng định nghĩa xét tính liên tục của hàm số f(x) = x³ + 2x – 1 tại x₀ = –1.

Hướng dẫn giải

Vậy hàm số đã cho liên tục tại x₀ = –1.

Bài 2. Xét tính liên tục của các hàm số sau trên tập xác định của hàm số đó:

a) f(x) = x + sinx;

.

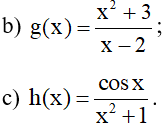
Hướng dẫn giải

a) Hàm số f(x) có tập xác định là ℝ.

Hai hàm số x và sinx liên tục trên ℝ nên hàm số f(x) = x + sinx liên tục trên ℝ.

b) Hàm số 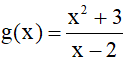 có tập xác định là ℝ\{2}.

Do đó hàm số 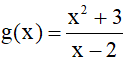 liên tục trên mỗi khoảng (–∞; 2) và (2; +∞).

c) Hàm số h(x) có tập xác định là ℝ.

Vì tử thức cosx liên tục ℝ và mẫu thức x² + 1 ≠ 0 liên tục trên ℝ.

Vậy h(x) liên tục trên ℝ.

Bài 3. Xét tính liêm tục của hàm số 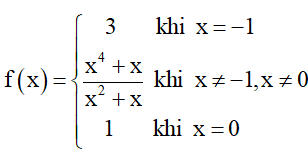  trên tập xác định của nó.

Hướng dẫn giải

Hàm số có TXĐ: D = ℝ.

Hàm số liên tục trên mỗi khoảng (–∞; –1); (–1; 0)  và (0; +∞).

• Tại x = –1, ta có:

⇒ Hàm số f(x) liên tục tại x = –1.

• Tại x = 0, ta có:

⇒ Hàm số f(x) liên tục tại x = 0.

Vậy hàm số f(x) liên tục tại mọi điểm x ∈ ℝ.

Bài 4. Tìm giá trị của tham số m để hàm số 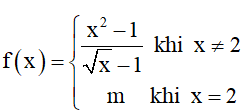 liên tục trên đoạn [0; 2].

Hướng dẫn giải

Hàm số xác định trên [0; 2] và liên tục trên [0; 2).

Khi đó để f(x) liên tục trên đoạn [0; 2] thì hàm số liên tục tại x = 2.

Tức là ta cần có:

Ta có: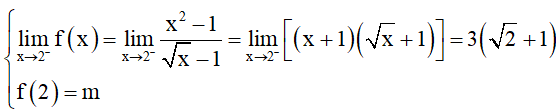     

Do đó (*) xảy ra khi và chỉ khi .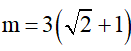

Học tốt Hàm số liên tục

Các bài học để học tốt Hàm số liên tục Toán lớp 11 hay khác:

15 Bài tập Hàm số liên tục (có đáp án) - Cánh diều Trắc nghiệm Toán 11

Với 15 bài tập trắc nghiệm Hàm số liên tục Toán lớp 11 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Cánh diều sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 11.

15 Bài tập Hàm số liên tục (có đáp án) - Cánh diều Trắc nghiệm Toán 11

Nội dung đang được cập nhật ...

Xem thêm bài tập trắc nghiệm Toán lớp 11 Cánh diều có đáp án hay khác: