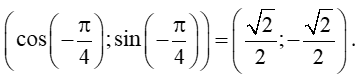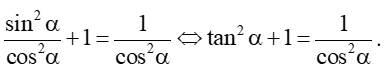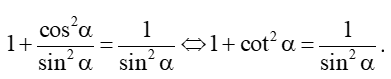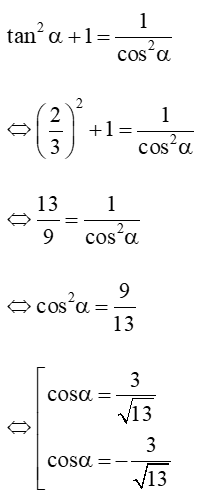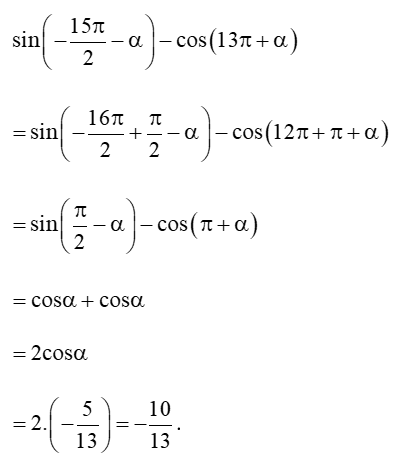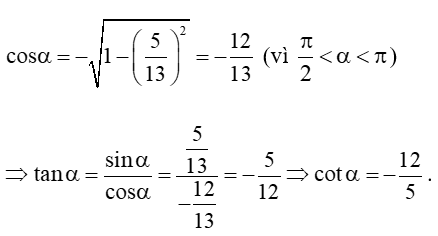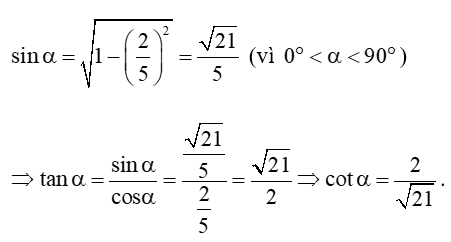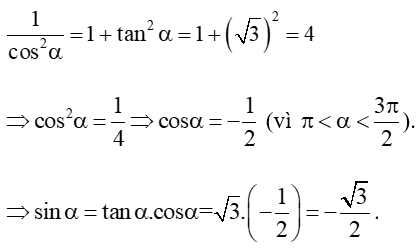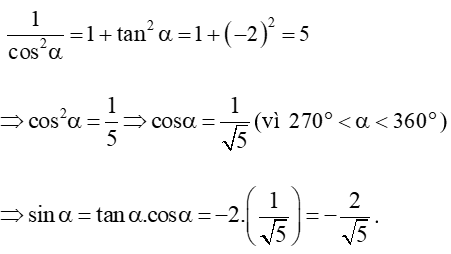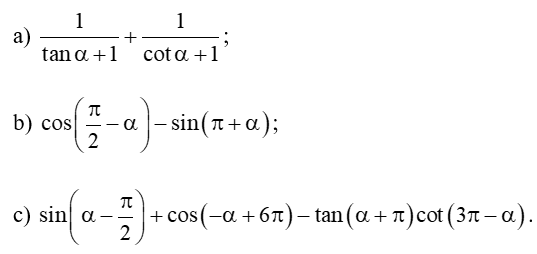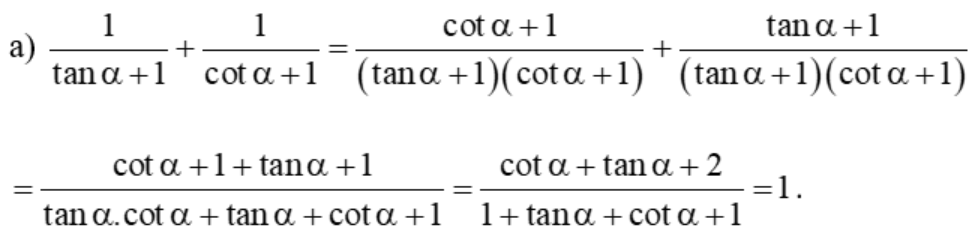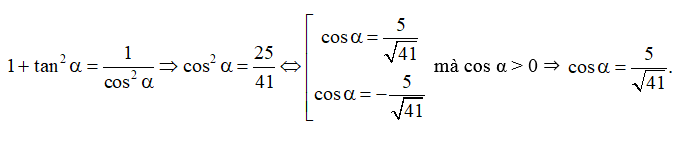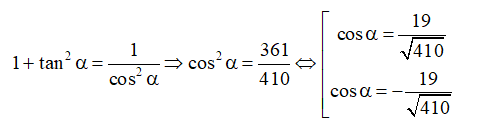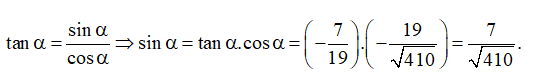Với giải bài tập Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh lớp 11 dễ dàng làm bài tập Toán 11 Bài 2.

Giải Toán 11 Chân trời sáng tạo Bài 2: Giá trị lượng giác của một góc lượng giác

Giải Toán 11 trang 13

Hoạt động khởi động trang 13 Toán 11 Tập 1 Chân trời sáng tạo

Giải Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác - Chân trời sáng tạo

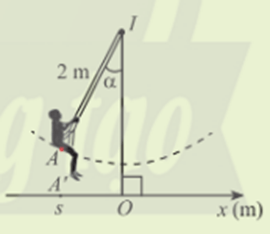
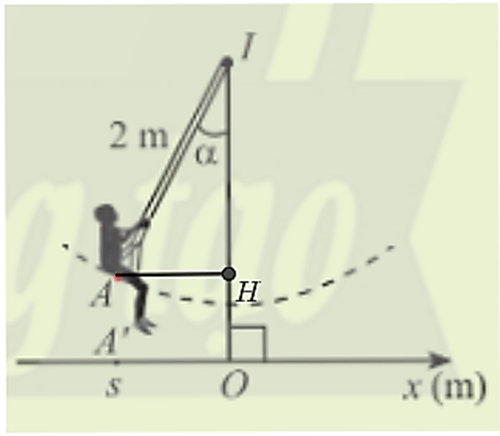
Hoạt động khởi động trang 13 Toán 11 Tập 1: Hình bên biểu diễn xích đu IA có độ dài 2m dao động quanh trục IO vuông góc với trục Ox trên mặt đất và A’ là hình chiếu của A lên Ox. Tọa độ s của A’ trên trục Ox được gọi là li độ của A và (IO, IA) = α được gọi là li độ góc của A. Làm cách nào để tính li độ dựa vào li độ góc?

Lời giải:

Kẻ AH vuông góc với IO tại H

Xét tam giác AHI vuông tại H, có:

AH = sinα . IA = 2sinα (m).

AH cũng chính là li độ của A nên s = 2sinα.

Lời giải bài tập Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác hay, chi tiết khác:

Hoạt động khám phá 1 trang 13 Toán 11 Tập 1 Chân trời sáng tạo

Giải Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác - Chân trời sáng tạo

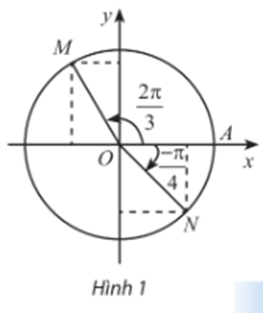
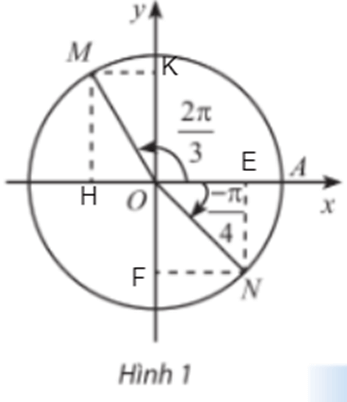
Hoạt động khám phá 1 trang 13 Toán 11 Tập 1: Trong Hình 1, M và N là điểm biểu diễn của các góc lượng giác $\frac{2\pi }{3}$ và $-\frac{\pi }{4}$ trên đường tròn lượng giác. Xác định tọa độ của M và N trong hệ trục tọa độ Oxy.

Lời giải:

Gọi H, K lần lượt là hình chiếu của điểm M xuống trục Ox và Oy; gọi E, F lần lượt là hình chiếu của điểm N trên trục Ox và Oy.

Đặt (OA, OM) = $\alpha$, (OA, ON) = $\beta$.

+) Xét tam giác MHO vuông tại H, có:

MH = sin$\widehat{MOH}$.MO = sin$\widehat{MOH}$

Ta có $\widehat{MOH}+\widehat{AOM}=180°$ nên sin$\widehat{MOH}$ = sin$\widehat{AOM}$.

⇒ MH = sin$\widehat{AOM}$ = sinα.

Mà MH = OK nên OK = sinα hay tung độ điểm M bằng sinα.

Ta lại có: OH = cos$\widehat{MOH}$.MO = cos$\widehat{MOH}$

Mà $\widehat{MOH}+\widehat{AOM}=180°$ nên cos$\widehat{MOH}$ = -cos$\widehat{AOM}$

⇒ OH = -cos$\widehat{AOM}$ = – cosα do đó hoành độ của điểm M bằng cosα.

Vậy tọa độ điểm M là (cosα; sinα) = $\left(\text{cos}\frac{2\pi }{3};\sin \frac{2\pi }{3}\right)=\left(-\frac{1}{2};\frac{\sqrt{3}}{2}\right)$.

+) Xét tam giác ONE vuông tại E, có:

NE = sin$\widehat{NOE}$.ON = sin$\widehat{NOE}$

Mà $\widehat{NOE}$= -$\beta$

⇒ NE = – sinβ.

Mà NE = OF nên OF = – sinβ do đó tung độ điểm N bằng sinβ.

Ta lại có: OE = cos$\widehat{NOE}$.ON = cos$\widehat{NOE}$

⇒ OE = cosβ nên hoành độ của điểm M bằng cosβ.

Vậy tọa độ điểm N là

(cosβ; sinβ) =

Lời giải bài tập Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác hay, chi tiết khác:

Thực hành 1 trang 15 Toán 11 Tập 1 Chân trời sáng tạo

Giải Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác - Chân trời sáng tạo

Thực hành 1 trang 15 Toán 11 Tập 1: Tính sin$\left(-\frac{2\pi }{3}\right)$ và tan495°.

Lời giải:

Ta có: sin$\left(-\frac{2\pi }{3}\right)$ = -sin$\left(\frac{2\pi }{3}\right)$ = $-\frac{\sqrt{3}}{2}$.

Ta có tan495° = – tan135° = – tan45° = $-\frac{\text{cos}45°}{\sin 45°}$ = -1.

Lời giải bài tập Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác hay, chi tiết khác:

Thực hành 2 trang 16 Toán 11 Tập 1 Chân trời sáng tạo

Giải Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác - Chân trời sáng tạo

Thực hành 2 trang 16 Toán 11 Tập 1: Sử dụng máy tính cầm tay để tính cos75° và tan$\left(\frac{-19\pi }{6}\right)$.

Lời giải:

Sử dụng máy tính cầm tay ta tính được:

cos75° = $\frac{\sqrt{6}-\sqrt{2}}{4}$;

tan$\left(\frac{-19\pi }{6}\right)=-\frac{\sqrt{3}}{3}$.

Lời giải bài tập Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác hay, chi tiết khác:

Hoạt động khám phá 2 trang 16 Toán 11 Tập 1 Chân trời sáng tạo

Giải Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác - Chân trời sáng tạo

Hoạt động khám phá 2 trang 16 Toán 11 Tập 1:

a) Trong Hình 5, M là điểm biểu diễn của góc lượng giác α trên đường tròn lượng giác. Giải thích vì sao sin²α + cos²α = 1.

b) Chia cả hai vễ của biểu thức ở câu a) cho cos²α ta được đẳng thức nào?

c) Chia cả hai vế của biểu thức ở câu a) cho sin²α ta được đẳng thức nào?

Lời giải:

a) M là điểm biểu diễn của góc lượng giác α trên đường tròn lượng giác nên tọa độ điểm M là (cosα; sinα) nên MH = sinα, OH = cosα.

Ta lại có: MH² + OH² = 1 (định lí Pythagore)

Hay sin²α + cos²α = 1.

b) Vì OH = cosα > 0 nên cos²α ≠ 0 nên chia cả hai vế của biểu thức của câu a) cho cos²α, ta được:

c) Vì MH = sinα > 0 nên sin²α ≠ 0 nên chia cả hai vế của biểu thức của câu a) cho sin²α, ta được:

Lời giải bài tập Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác hay, chi tiết khác:

Thực hành 3 trang 17 Toán 11 Tập 1 Chân trời sáng tạo

Giải Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác - Chân trời sáng tạo

Thực hành 3 trang 17 Toán 11 Tập 1: Cho tan$\alpha =\frac{2}{3}$ với $\pi <\alpha <\frac{3\pi }{2}$. Tính cosα và sinα.

Lời giải:

Ta có:

Vì $\pi <\alpha <\frac{3\pi }{2}$ nên điểm biểu diễn của góc α trên đường tròn lượng giác thuộc góc phần tư thứ III, do đó cosα < 0 nên cos$\alpha =-\frac{3}{\sqrt{13}}$.

⇒ sinα = tanα.cosα = tan$\alpha$.cos$\alpha$ = $\frac{2}{3}.\left(-\frac{3}{\sqrt{13}}\right)=-\frac{2}{\sqrt{13}}$.

Lời giải bài tập Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác hay, chi tiết khác:

Hoạt động khám phá 3 trang 17 Toán 11 Tập 1 Chân trời sáng tạo

Giải Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác - Chân trời sáng tạo

Hoạt động khám phá 3 trang 17 Toán 11 Tập 1: Cho $\alpha =\frac{\pi }{3}$. Biểu diễn các góc lượng giác – α, α + π, π – α, $\frac{\pi }{2}-\alpha$ trên đường tròn lượng giác và rút ra mối liên hệ giữa giá trị lượng giác của các góc này với giá trị lượng giác của góc α.

Lời giải:

Biểu diễn góc lượng giác $-\frac{\pi }{3}$:

Biểu diễn góc lượng giác $\frac{\pi }{3}+\pi =\frac{4\pi }{3}$:

Biểu diễn góc lượng giác $\pi -\frac{\pi }{3}=\frac{2\pi }{3}$:

Biểu diễn góc lượng giác $\frac{\pi }{2}-\frac{\pi }{3}=\frac{\pi }{6}$

Lời giải bài tập Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác hay, chi tiết khác:

Thực hành 4 trang 19 Toán 11 Tập 1 Chân trời sáng tạo

Giải Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác - Chân trời sáng tạo

Thực hành 4 trang 19 Toán 11 Tập 1:

a) Biểu diễn cos638° qua giá trị lượng giác của góc có số đo từ 0° đến 45°.

b) Biểu diễn cot$\frac{19\pi }{5}$ qua giá trị lượng giác của góc có số đo từ 0 đến $\frac{\pi }{4}$.

Lời giải:

a) Ta có: cos638° = cos(2.360° + (– 82°)) = cos(– 82°) = cos82° = cos(90° – 8°) = sin8°.

b) Ta có: $\cot \frac{19\pi }{5}=\cot \left(4\pi -\frac{\pi }{5}\right)=\cot \left(-\frac{\pi }{5}\right)=-\cot \frac{\pi }{5}$.

Lời giải bài tập Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác hay, chi tiết khác:

Vận dụng trang 19 Toán 11 Tập 1 Chân trời sáng tạo

Giải Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác - Chân trời sáng tạo

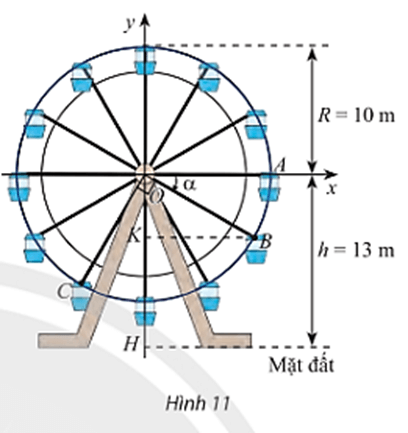
Vận dụng trang 19 Toán 11 Tập 1: Trong Hình 11, vị trí cabin mà Bình và Cường ngồi trên vòng quay được đánh dấu bởi điểm B và C.

a) Chứng minh rằng chiều cao từ điểm B đến mặt đất bằng (13 + 10sinα) mét với α là số đo của một góc lượng giác tia đầu OA, tia cuối OB. Tính độ cao của điểm B so với mặt đất khi α = – 30°.

b) Khi điểm B cách mặt đất 4m thì điểm C cách mặt đất bao nhiêu mét? Làm tròn kết quả đến hàng phần trăm.

Lời giải:

a) Ta có điểm B là điểm biểu diễn cho góc lượng giác có số đo góc là α trên đường tròn lượng giác có bán kính bằng 10 nên tọa độ điểm B(10cosα; 10sinα).

Vì vậy chiều cao từ điểm B đến mặt đất là: 13 + 10sinα (mét).

Với α = – 30° ta có chiều cao từ điểm B đến mặt đất là: 13 + 10sin.(– 30°) = 8 (mét).

b) Đặt (OA, OC) = β = α – 90°

Nếu điểm B cách mặt đất 4m thì 13 + 10sinα = 4

⇔ sinα = $-\frac{9}{10}$

Ta có sinα = cos(α – 90°) = $-\frac{9}{10}$

⇒ cos(α – 90°) = $-\frac{9}{10}$

⇒ cosβ = $-\frac{9}{10}$

⇒ sinβ = $-\sqrt{1^2-{\left(\frac{9}{10}\right)}^2}=-\frac{\sqrt{19}}{10}$

Vì vậy chiều cao từ điểm C đến mặt đất là: 13 + 10sinβ = 13 + 10.$\left(-\frac{\sqrt{19}}{10}\right)$ ≈ 8,64 (mét).

Lời giải bài tập Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác hay, chi tiết khác:

Bài 1 trang 19 Toán 11 Tập 1 Chân trời sáng tạo

Giải Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác - Chân trời sáng tạo

Bài 1 trang 19 Toán 11 Tập 1: Các đẳng thức sau có thể đồng thời xảy ra không?

a) sinα = $\frac{3}{5}$ và cosα = $-\frac{4}{5}$;

b) sinα = $\frac{1}{3}$ và cotα = $\frac{1}{2}$;

c) tanα = 3 và cotα = $\frac{1}{3}$.

Lời giải:

a) Với – 1 ≤ sinα = $\frac{3}{5}$ ≤ 1 và – 1 ≤ cosα = $-\frac{4}{5}$ ≤ 1, ta có:

sin²α + cos²α = ${\left(\frac{3}{5}\right)}^2+{\left(-\frac{4}{5}\right)}^2$= 1.

Vậy sinα = $\frac{3}{5}$ và cosα = $-\frac{4}{5}$ có thể đồng thời xảy ra.

b) Với – 1 ≤ sinα = $\frac{1}{3}$ ≤ 1 và cotα = $\frac{1}{2}$, ta có:

1 + cot²α = $1+{\left(\frac{1}{2}\right)}^2=1+\frac{1}{4}=\frac{5}{4}$

$\frac{1}{{\sin }^2\alpha }=\frac{1}{{\left(\frac{1}{3}\right)}^2}=9$

Do đó 1 + cot²α ≠ $\frac{1}{{\sin }^2\alpha }$.

Vì vậy sinα = $\frac{1}{3}$ và cotα = $\frac{1}{2}$ không đồng thời xảy ra.

c) Với tanα = 3 và cotα = $\frac{1}{3}$, ta có:

tanα . cotα = 3. $\frac{1}{3}$ = 1.

Vì vậy tanα = 3 và cotα = $\frac{1}{3}$ đồng thời xảy ra.

Lời giải bài tập Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác hay, chi tiết khác:

Bài 2 trang 19 Toán 11 Tập 1 Chân trời sáng tạo

Giải Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác - Chân trời sáng tạo

Bài 2 trang 19 Toán 11 Tập 1: Cho sinα = $\frac{12}{13}$ và cosα = $-\frac{5}{13}$. Tính $\sin \left(-\frac{15\pi }{2}-\alpha \right)-\text{cos}\left(13\pi +\alpha \right)$.

Lời giải:

Lời giải bài tập Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác hay, chi tiết khác:

Bài 3 trang 19 Toán 11 Tập 1 Chân trời sáng tạo

Giải Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác - Chân trời sáng tạo

Bài 3 trang 19 Toán 11 Tập 1: Tính các giá trị lượng giác của góc α, nếu:

a) sin$\alpha$ = $\frac{5}{13}$ và $\frac{\pi }{2}<\alpha <\pi$;

b) cos$\alpha$ = $\frac{2}{5}$ và $0°<\alpha <90°$;

c) tan$\alpha$ = $\sqrt{3}$ và $\pi <\alpha <\frac{3\pi }{2}$;

d) cot$\alpha$ = $\frac{1}{2}$ và $270°<\alpha <360°$.

Lời giải:

a) Ta có:

Vậy $\text{cos}\alpha =-\frac{12}{13},\tan \alpha =-\frac{5}{12},\cot \alpha =-\frac{12}{5}$.

b) Ta có:

Vậy $\sin \alpha =\frac{\sqrt{21}}{5},\tan \alpha =\frac{\sqrt{21}}{2},\cot \alpha =\frac{2}{\sqrt{21}}$.

c) Ta có: tan$\alpha$ = $\sqrt{3}$$\Rightarrow$cot$\alpha$ = $\frac{1}{\sqrt{3}}$

Ta lại có:

Vậy $\sin \alpha =-\frac{\sqrt{3}}{2},\text{cos}\alpha =-\frac{1}{2},\cot \alpha =\frac{1}{\sqrt{3}}$.

d) Ta có: $\text{cot}\alpha =-\frac{1}{2}\Rightarrow \text{tan}\alpha =-2$

Ta lại có:

Vậy $\sin \alpha =-\frac{2}{\sqrt{5}},\text{cos}\alpha =\frac{1}{\sqrt{5}},\tan \alpha =-2$.

Lời giải bài tập Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác hay, chi tiết khác:

Bài 4 trang 19 Toán 11 Tập 1 Chân trời sáng tạo

Giải Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác - Chân trời sáng tạo

Bài 4 trang 19 Toán 11 Tập 1: Biểu diễn các giá trị lượng giác sau qua các giá trị lượng giác của góc có số đo từ 0 đến $\frac{\pi }{4}$ hoặc từ 0 đến 45° và tính:

a) cos$\frac{21\pi }{6}$;

b) sin$\frac{129\pi }{4}$;

c) tan1 020°.

Lời giải:

a) Ta có: .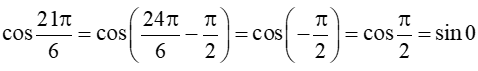

b) .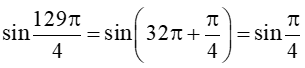

c) tan1 020° = tan(3.180° – 60°) = tan(180° – 60°) = – tan60° = – cot30°.

Lời giải bài tập Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác hay, chi tiết khác:

Bài 5 trang 19 Toán 11 Tập 1 Chân trời sáng tạo

Giải Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác - Chân trời sáng tạo

Bài 5 trang 19 Toán 11 Tập 1: Chứng minh đẳng thức lượng giác sau:

a) sin⁴α – cos⁴α = 1 – 2cos²α;

b) tanα + cotα = $\frac{1}{\sin \alpha .\text{cos}\alpha }$.

Lời giải:

a) Ta có: sin⁴α – cos⁴α = (sin²α – cos²α).(sin²α + cos²α ) = sin²α + cos²α – 2cos²α = 1 – 2cos²α.

b) Ta có: tanα + cotα =

.

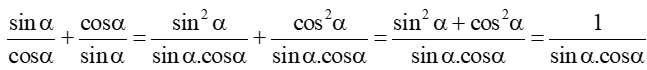
Lời giải bài tập Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác hay, chi tiết khác:

Bài 6 trang 19 Toán 11 Tập 1 Chân trời sáng tạo

Giải Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác - Chân trời sáng tạo

Bài 6 trang 19 Toán 11 Tập 1: Rút gọn các biểu thức sau:

Lời giải:

b) cos$\left(\frac{\pi }{2}-\alpha \right)$ − sin$\left(\pi +\alpha \right)$ = sinα – (−sinα) = sinα + sinα = 2sinα.

c) sin$\left(\alpha -\frac{\pi }{2}\right)$ + cos$\left(-\alpha +6\pi \right)$ − tan$\left(\alpha +\pi \right)$.cot$\left(3\pi -\alpha \right)$

= −sin$\left(\frac{\pi }{2}-\alpha \right)$ + cos$\left(6\pi -\alpha \right)$ − tan$\left(\alpha +\pi \right)$.cot$\left(2\pi +\pi -\alpha \right)$

= −cosα + cosα – tanα.(−cotα).

= 0 + tanα.cotα

= 1.

Lời giải bài tập Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác hay, chi tiết khác:

Bài 7 trang 20 Toán 11 Tập 1 Chân trời sáng tạo

Giải Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác - Chân trời sáng tạo

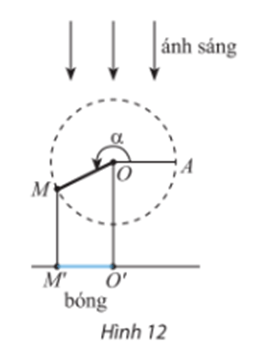
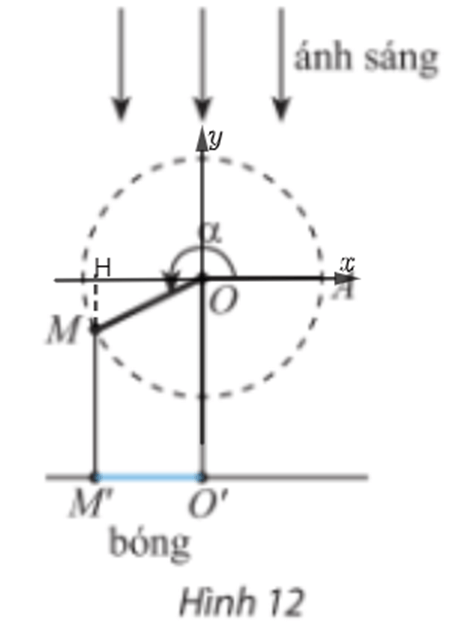
Bài 7 trang 20 Toán 11 Tập 1: Thanh OM quay ngược chiều kim đồng hồ quanh trục O của nó trên một mặt phẳng thẳng đứng và in bóng vuông góc xuống mặt đất như Hình 12. Vị trí ban đầu của thanh là OA. Hỏi độ dài bóng O’M’ của OM khi thanh quay được $3\frac{1}{10}$ vòng là bao nhiêu, biết độ dài thanh OM là 15 cm? Kết quả làm tròn đến hàng phần mười.

Lời giải:

Đặt hệ trục tọa độ như hình vẽ:

Kẻ MH vuông góc với Ox.

Điểm M là điểm biểu diễn góc lượng giác α

Ta có: $\alpha =3\frac{1}{10}.360°=1116°$

Khi đó M(cos1116°.15; sin1116°.15)

Suy ra OH = |cos1116°|.15 ≈12,1.

Vậy độ dài bóng O’M’ của OM khi thanh quay được $3\frac{1}{10}$ vòng là 12,1 cm.

Lời giải bài tập Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác hay, chi tiết khác:

Bài 8 trang 20 Toán 11 Tập 1 Chân trời sáng tạo

Giải Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác - Chân trời sáng tạo

Bài 8 trang 20 Toán 11 Tập 1: Khi đạp xe di chuyển, van V của bánh xe quay quanh trục O theo chiều kim đồng hồ với tốc độ góc không đổi là 11 rad/s (Hình 13). Ban đầu van nằm ở vị trí A. Hỏi sau một phút di chuyển , khoảng cách từ van đến mặt đất là bao nhiêu, biết bán kính OA = 58 cm? Giả sử độ dàu của lốp xe không đáng kể. Kết quả làm tròn đến hàng phần mười.

Lời giải:

Sau một phút di chuyển, van V đã quay được một góc lượng giác có số đo góc là: α = 11.60 = 660 (rad).

Khi đó tọa độ điểm V biểu diễn cho góc lượng giác trên có tọa độ là:

V(58.cosα; 58.sinα) ≈ (56; 15,2)

Khi đó khoảng cách từ van đến mặt đất khoảng 58 – 15,2 = 42,8 cm.

Lời giải bài tập Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác hay, chi tiết khác:

SBT Toán 11 Chân trời sáng tạo Bài 2: Giá trị lượng giác của một góc lượng giác

Với giải sách bài tập Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 11 Bài 2.

Giải SBT Toán 11 Chân trời sáng tạo Bài 2: Giá trị lượng giác của một góc lượng giác

Giá trị lượng giác của một góc lượng giác (Lý thuyết Toán lớp 11) | Chân trời sáng tạo

Với tóm tắt lý thuyết Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 11 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 11.

Giá trị lượng giác của một góc lượng giác (Lý thuyết Toán lớp 11) | Chân trời sáng tạo

Lý thuyết Giá trị lượng giác của một góc lượng giác

1. Giá trị lượng giác của góc lượng giác

- Trên đường tròn lượng giác, gọi M là điểm biểu diễn góc lượng giác có số đo α. Khi đó:

• Tung độ y_M của M gọi là sin của α, kí hiệu sin α.

• Hoành độ x_M của M gọi là côsin của α, kí hiệu cos α.

• Nếu x_M ≠ 0 thì tỉ số $\frac{y_M}{x_M}=\frac{\sin \alpha }{\cos \alpha }$ gọi là tang của α, kí hiệu tan α.

• Nếu y_M ≠ 0 thì tỉ số $\frac{x_M}{y_M}=\frac{\cos \alpha }{\sin \alpha }$ gọi là côtang của α, kí hiệu cot α.

Các giá trị sin α, cos α, tan α và cot α được gọi là các giá trị lượng giác của góc lượng giác α.

Chú ý:

• Ta gọi trục hoành là trục côsin, còn trục tung là trục sin.

• Trục As có gốc ở điểm A(1; 0) và song song với trục sin gọi là trục tang. Nếu đường thẳng OM cắt trục tang thì tung độ của giao điểm đó chính là tan α.

• Trục Bt có gốc ở điểm B(0; 1) và song song với trục côsin gọi là trục côtang. Nếu đường thẳng OM cắt trục côtang thì hoành độ của giao điểm đó chính là cot α.

• sin α và cos α xác định với mọi α ∈ ℝ;

tan α chỉ xác định với các góc $\alpha \ne \frac{\pi }{2}+k\pi \text{\hspace{0.17em}\hspace{0.17em}(}\left(k\in \mathbb{Z}\right));$

cot α chỉ xác định với các góc α ≠ kπ (k ∈ ℤ).

• Với mọi góc lượng giác α và số nguyên k, ta có:

sin(α + k2π) = sin α;                            tan(α + kπ) = tan α;

cos(α + k2π) = cos α;                           cot(α + kπ) = cot α.

• Ta có thể sử dụng đường tròn lượng giác để xác định giá trị lượng giác của góc α.

Ví dụ: Theo đường tròn lượng giác, ta thấy điểm biểu diễn của góc $-\frac{\pi }{3}$ và góc $\frac{\pi }{3}$ đối xứng nhau qua trục hoành, nên chúng có cùng hoành độ và tung độ đối nhau. Do đó ta có:

2. Tính giá trị lượng giác của một góc bằng máy tính cầm tay

Giá trị lượng giác của một góc bất kỳ có thể tính bằng máy tính cầm tay.

Chú ý:

• Trước khi tính, cần chọn đơn vị đo góc bằng cách:

+ Ấn các phím SHIFT, MENU và 2 để màn hình hiện lên bảng lựa chọn đơn vị đo góc bao gồm: Degree, Radian và Gradian.

+ Tiếp tục ấn phím 1 để chọn đơn vị độ (Degree) hoặc phím 2 để chọn đơn vị radian (Radian).

+ Cuối cùng ấn phím MENU và 1 để vào chế độ tính toán.

3. Hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác

Ta có những hệ thức sau liên hệ giữa các giá trị lượng giác của cùng một góc lượng giác α:

• sin²α + cos²α = 1                                        

• tan α . cot α = 1 với $\alpha \ne k\frac{\pi }{2},$ k ∈ ℤ

• $1+{\tan }^2\alpha =\frac{1}{{\cos }^2\alpha }$ với $\alpha \ne \frac{\pi }{2}+k\pi ,$ k ∈ ℤ 

• $1+{\cot }^2\alpha =\frac{1}{{\sin }^2\alpha }$ với α ≠ kπ, k ∈ ℤ

Ví dụ: Cho $\cos \alpha =\frac{4}{13}\left(\mathrm{(0}<\alpha <\frac{\pi }{2}\right)$):

mà $0<\alpha <\frac{\pi }{2}\Rightarrow \sin \alpha >0\Rightarrow \sin \alpha =\sqrt{\frac{153}{169}}=\frac{3\sqrt{17}}{13}.$

$\tan \alpha =\frac{\sin \alpha }{\cos \alpha }=\frac{3\sqrt{17}}{13}:\frac{4}{13}=\frac{3\sqrt{17}}{4}$.

$\cot \alpha =\frac{1}{\tan \alpha }=\frac{4}{3\sqrt{17}}$.

4. Giá trị lượng giác của các góc lượng giác có liên quan đặc biệt

4.1. Hai góc đối nhau: 𝛂 và –𝛂

4.2. Hai góc hơn kém nhau 𝛑: 𝛂 và 𝛂 + 𝛑

4.3. Hai góc bù nhau: 𝛂 và 𝛑 – 𝛂

4.4. Hai góc phụ nhau: 𝛂 và $\frac{\pi }{2}-\mathrm{\alpha }$

Ví dụ: Biểu diễn $\cos \frac{5\pi }{12}$ qua giá trị lượng giác của góc có số đo từ 0 đến $\frac{\pi }{4}.$

Bài tập Giá trị lượng giác của một góc lượng giác

Bài 1. Tính các giá trị lượng giác của góc α biết:

a) $\tan \alpha =-\frac{4}{5}$ biết $\frac{3\pi }{2}<\alpha <2\pi .$

b) $\cot \alpha =-\frac{19}{7}$ biết $\frac{\pi }{2}<\alpha <\pi .$

Hướng dẫn giải

a) Do $\frac{3\pi }{2}<\alpha <2\pi$ nên sin α < 0, cos α > 0, cot α < 0.

Ta có:

$\cot \alpha =\frac{1}{\tan \alpha }\Rightarrow \cot \alpha =-\frac{5}{4}.$

$\tan \alpha =\frac{\sin \alpha }{\cos \alpha }\Rightarrow \sin \alpha =\tan \alpha .\cos \alpha =-\frac{4}{5}.\frac{5}{\sqrt{41}}=-\frac{4\sqrt{41}}{41}.$

b) Do $\frac{\pi }{2}<\alpha <\pi$ nên sin α > 0, cos α < 0, tan α < 0.

Ta có:

$\tan \alpha =\frac{1}{\cot \alpha }\Rightarrow \tan \alpha =-\frac{7}{19}.$

Mà cos α < 0 ⇒ $\cos \alpha =-\frac{19}{\sqrt{410}}.$

Bài 2. Rút gọn các biểu thức sau:

a) A = (1 – sin²α).cot²α + 1 – cot²α;

b) $B=\frac{2{\cos }^2\alpha -1}{\sin \alpha +\cos \alpha }$.

Hướng dẫn giải

a) A = (1 – sin²α).cot²α + 1 – cot²α

⇔ A = cot²α – sin²α.cot²α + 1 – cot²α

⇔ $A=1-{\sin }^2\alpha .\frac{{\cos }^2\alpha }{{\sin }^2\alpha }={\sin }^2\alpha .$

b) $B=\frac{2{\cos }^2\alpha -1}{\sin \alpha +\cos \alpha }$

⇔ $B=\frac{{\cos }^2\alpha -{\sin }^2\alpha }{\sin \alpha +\cos \alpha }$

⇔ B = cos α – sin α.

Bài 3. Cho $\tan \alpha =\frac{3}{5}.$ Tính: $A=\frac{\sin \alpha \cos \alpha }{{\sin }^2\alpha -{\cos }^2\alpha }.$

Hướng dẫn giải

Chia cả tử và mẫu của biểu thức A cho cos²α ta được:

$A=\frac{\sin \alpha \cos \alpha }{{\sin }^2\alpha -{\cos }^2\alpha }=\frac{\tan \alpha }{{\tan }^2\alpha -1}=-\frac{15}{16}.$

Học tốt Giá trị lượng giác của một góc lượng giác

Các bài học để học tốt Giá trị lượng giác của một góc lượng giác Toán lớp 11 hay khác: