Với giải bài tập Toán 11 Bài 12: Đường thẳng và mặt phẳng song song sách Kết nối tri thức hay nhất, chi tiết giúp học sinh lớp 11 dễ dàng làm bài tập Toán 11 Bài 12.

Giải Toán 11 Kết nối tri thức Bài 12: Đường thẳng và mặt phẳng song song

Giải Toán 11 trang 84

Mở đầu trang 84 Toán 11 Tập 1 - Kết nối tri thức

Giải Toán 11 Bài 12: Đường thẳng và mặt phẳng song song - Kết nối tri thức

Mở đầu trang 84 Toán 11 Tập 1: Khi xây tường gạch, người thợ thường bắt đầu với việc xây các viên gạch dẫn, sau đó căng dây nhợ dọc theo cạnh của các viên gạch dẫn đó để làm chuẩn rồi mới xây các viên gạch tiếp theo. Việc sử dụng dây căng như vậy có tác dụng gì? Toán học mô tả vị trí giữa dây căng, các mép gạch với mặt đất như thế nào?

Lời giải:

Sau bài học này ta sẽ giải quyết được vấn đề trên như sau:

Dây nhợ được cang dọc theo cạnh của các viên gạch dẫn, lúc này dây nhợ sẽ là một đường thẳng song song với mặt đất. Khi người thợ tiếp tục xây các viên gạch tiếp theo theo dây nhợ thì hàng gạch tiếp theo sẽ thẳng hàng và bằng, đảm bảo độ thẳng đứng và bằng phẳng cho tường được xây ra.

Toán học mô tả vị trí giữa dây căng, các mép gạch với mặt đất là các đường thẳng song song với mặt phẳng.

Lời giải bài tập Toán 11 Bài 12: Đường thẳng và mặt phẳng song song hay, chi tiết khác:

HĐ1 trang 84 Toán 11 Tập 1 - Kết nối tri thức

Giải Toán 11 Bài 12: Đường thẳng và mặt phẳng song song - Kết nối tri thức

HĐ1 trang 84 Toán 11 Tập 1: Quan sát hình ảnh khung thành bóng đá và nhận xét vị trí của xà ngang, cột dọc, thanh chống và thanh bên của khung thành với mặt đất.

Lời giải:

Từ hình vẽ ta thấy:

- Xà ngang nằm phía trên và không có điểm chung với mặt đất;

- Cột dọc thẳng đứng và có 1 điểm chung với mặt đất;

- Thanh chống nằm xiên và có 1 điểm chung với mặt đất;

- Thanh bên nằm hoàn toàn trên mặt đất, có vô số điểm chung với mặt đất.

Lời giải bài tập Toán 11 Bài 12: Đường thẳng và mặt phẳng song song hay, chi tiết khác:

Câu hỏi trang 85 Toán 11 Tập 1 - Kết nối tri thức

Giải Toán 11 Bài 12: Đường thẳng và mặt phẳng song song - Kết nối tri thức

Câu hỏi trang 85 Toán 11 Tập 1: Hãy chỉ ra một hình ảnh đường thẳng song song với mặt phẳng trong bức ảnh bên (H.4.34).

Lời giải:

Quan sát hình ảnh đã cho ta thấy đường thẳng được tạo bởi thanh ngang của cây cầu song song với mặt nước lúc tĩnh lặng.

Lời giải bài tập Toán 11 Bài 12: Đường thẳng và mặt phẳng song song hay, chi tiết khác:

Luyện tập 1 trang 85 Toán 11 Tập 1 - Kết nối tri thức

Giải Toán 11 Bài 12: Đường thẳng và mặt phẳng song song - Kết nối tri thức

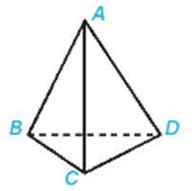
Luyện tập 1 trang 85 Toán 11 Tập 1: Trong Ví dụ 1, đường thẳng AC cắt các mặt phẳng nào, nằm trong các mặt phẳng nào?

Lời giải:

Đường thẳng AC cắt các mặt phẳng (BCD) và (ABD).

Đường thẳng AC nằm trong các mặt phẳng (ABC) và (ACD).

Lời giải bài tập Toán 11 Bài 12: Đường thẳng và mặt phẳng song song hay, chi tiết khác:

HĐ2 trang 85 Toán 11 Tập 1 - Kết nối tri thức

Giải Toán 11 Bài 12: Đường thẳng và mặt phẳng song song - Kết nối tri thức

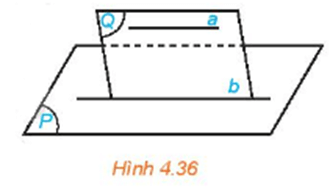
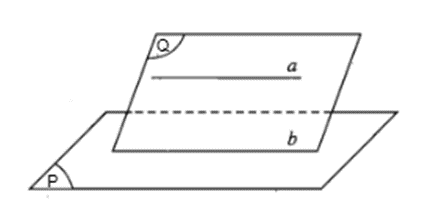
HĐ2 trang 85 Toán 11 Tập 1: Cho đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng b nằm trong (P). Gọi (Q) là mặt phẳng chứa a và b (H.4.36).

Nếu a và (P) cắt nhau tại điểm M thì M có thuộc (Q) và M có thuộc b hay không? Hãy rút ra kết luận sau khi trả lời các câu hỏi trên.

Lời giải:

Nếu a và (P) cắt nhau tại điểm M thì M có thuộc (Q) (do M thuộc a và a nằm trong (Q)).

Do đó, a cắt b tại M, vậy M thuộc b. Khi đó, M là điểm chung của và b, điều này trái với điều kiện a song song với b.

Kết luận: Nếu đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng b nằm trong (P) thì a song song với mặt phẳng (P).

Lời giải bài tập Toán 11 Bài 12: Đường thẳng và mặt phẳng song song hay, chi tiết khác:

Câu hỏi trang 85 Toán 11 Tập 1 - Kết nối tri thức

Giải Toán 11 Bài 12: Đường thẳng và mặt phẳng song song - Kết nối tri thức

Câu hỏi trang 85 Toán 11 Tập 1: Phát biểu trên còn đúng không nếu bỏ điều kiện “a không nằm trong mặt phẳng (P)”?

Lời giải:

Phát biểu trên không còn đúng nếu bỏ điều kiện “a không nằm trong mặt phẳng (P)” vì nếu a nằm trong mặt phẳng (P) thì a không thể song song với (P). Hơn nữa, (P) và (Q) sẽ trùng nhau và do đó không thể coi b là giao tuyến của (P) và (Q).

Lời giải bài tập Toán 11 Bài 12: Đường thẳng và mặt phẳng song song hay, chi tiết khác:

Luyện tập 2 trang 85 Toán 11 Tập 1 - Kết nối tri thức

Giải Toán 11 Bài 12: Đường thẳng và mặt phẳng song song - Kết nối tri thức

Luyện tập 2 trang 85 Toán 11 Tập 1: Trong Ví dụ 2, chứng minh rằng đường thẳng c song song với mp(a, b), đường thẳng b song song với mp(a, c).

Lời giải:

+) Ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng nên đường thẳng c không nằm trong mp(a, b). Vì đường thẳng c song song với đường thẳng b và đường thẳng b nằm trong mp(a, b) nên đường thẳng c song song với mp(a, b).

+) Ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng nên đường thẳng b không nằm trong mp(a, c). Vì đường thẳng b song song với đường thẳng a và đường thẳng a nằm trong mp(a, c) nên đường thẳng b song song với mp(a, c).

Lời giải bài tập Toán 11 Bài 12: Đường thẳng và mặt phẳng song song hay, chi tiết khác:

Luyện tập 1 trang 86 Toán 11 Tập 1 - Kết nối tri thức

Giải Toán 11 Bài 12: Đường thẳng và mặt phẳng song song - Kết nối tri thức

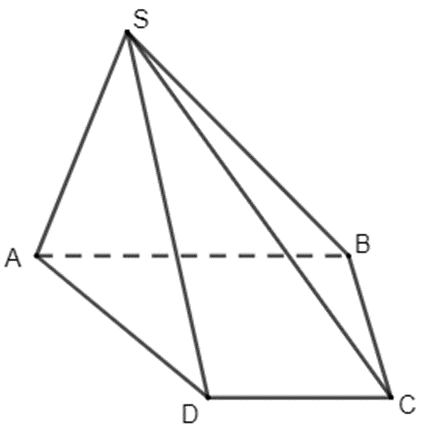
Luyện tập 1 trang 86 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy là hình thang (AB // CD). Hai đường thẳng SD và AB có chéo nhau hay không? Chỉ ra mặt phẳng chứa đường thẳng SD và song song với AB.

Lời giải:

Nếu hai đường thẳng SD và AB không chéo nhau thì SD và AB đồng phẳng hay bốn điểm S, A, B, D đồng phẳng, trái với giả thiết S.ABCD là hình chóp. Do đó, hai đường thẳng SD và AB chéo nhau.

Ta có đường thẳng AB không nằm trong mặt phẳng (SCD) và có AB // CD (giả thiết), đường thẳng CD nằm trong mặt phẳng (SCD), do đó đường thẳng AB song song với mặt phẳng (SCD). Mà mặt phẳng (SCD) chứa đường thẳng SD. Vậy mặt phẳng (SCD) chứa đường thẳng SD và song song với AB.

Lời giải bài tập Toán 11 Bài 12: Đường thẳng và mặt phẳng song song hay, chi tiết khác:

Vận dụng trang 86 Toán 11 Tập 1 - Kết nối tri thức

Giải Toán 11 Bài 12: Đường thẳng và mặt phẳng song song - Kết nối tri thức

Vận dụng trang 86 Toán 11 Tập 1: Trong tình huống mở đầu, hãy giải thích tại sao dây nhợ khi căng thì song song với mặt đất. Tác dụng của việc đó là gì?

Lời giải:

Dây nhợ được căng theo hàng gạch đầu tiên, các hàng gạch được xây thẳng hàng và mỗi viên gạch đều có cách cạnh đối diện song song với nhau, do đó mép trên của hàng gạch đầu là một đường thẳng song song với mặt đất nên dây nhợ khi căng song song với mặt đất. Tác dụng của việc căng dậy nhợ để xây tường có độ thẳng, đứng và bằng.

Lời giải bài tập Toán 11 Bài 12: Đường thẳng và mặt phẳng song song hay, chi tiết khác:

HĐ3 trang 86 Toán 11 Tập 1 - Kết nối tri thức

Giải Toán 11 Bài 12: Đường thẳng và mặt phẳng song song - Kết nối tri thức

HĐ3 trang 86 Toán 11 Tập 1: Cho đường thẳng a song song với mặt phẳng (P) và (Q) là một mặt phẳng chứa a. Giả sử (Q) cắt (P) theo giao tuyến b (H.4.36).

a) Hai đường thẳng a và b có thể chéo nhau hay không?

b) Hai đường thẳng a và b có thể cắt nhau không?

Lời giải:

a) Hai đường thẳng a và b đều nằm trong mặt phẳng (Q) nên hai đường thẳng này không thể chéo nhau.

b) Giả sử hai đường thẳng a và b cắt nhau tại điểm I. Khi đó I ∈ (P) vì I ∈ b và b ⊂ (P).

Mặt khác I ∈ a nên a cắt (P) tại I (vô lí do a song song với (P)). Vậy a // b hay hai đường thẳng a và b không thể cắt nhau.

Lời giải bài tập Toán 11 Bài 12: Đường thẳng và mặt phẳng song song hay, chi tiết khác:

Luyện tập 4 trang 87 Toán 11 Tập 1 - Kết nối tri thức

Giải Toán 11 Bài 12: Đường thẳng và mặt phẳng song song - Kết nối tri thức

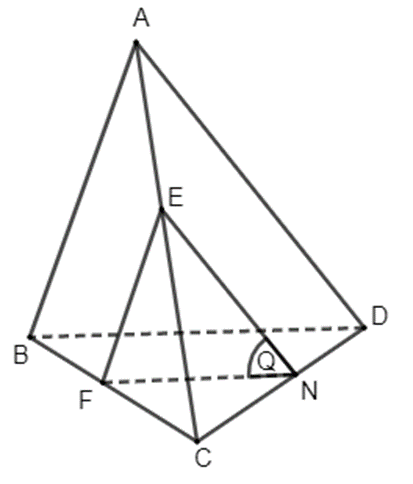
Luyện tập 4 trang 87 Toán 11 Tập 1: Trong Ví dụ 4, gọi (Q) là mặt phẳng qua E và song song với hai đường thẳng AB, AD. Xác định giao tuyến của (Q) với các mặt của tứ diện.

Lời giải:

Mặt phẳng (ABC) chứa đường thẳng AB song song với mặt phẳng (Q) nên mặt phẳng (ABC) cắt mặt phẳng (Q) theo giao tuyến song song với AB. Vẽ EF // AB (F thuộc BC) thì EF là giao tuyến của (Q) và (ABC).

Mặt phẳng (ACD) chứa đường thẳng AD song song với mặt phẳng (Q) nên mặt phẳng (ACD) cắt mặt phẳng (Q) theo giao tuyến song song với AD. Vẽ EN // AD (N thuộc CD) thì EN là giao tuyến của (Q) và (ACD). Khi đó FN là giao tuyến của (Q) và (BCD).

Lời giải bài tập Toán 11 Bài 12: Đường thẳng và mặt phẳng song song hay, chi tiết khác:

Bài 4.16 trang 87 Toán 11 Tập 1 - Kết nối tri thức

Giải Toán 11 Bài 12: Đường thẳng và mặt phẳng song song - Kết nối tri thức

Bài 4.16 trang 87 Toán 11 Tập 1: Trong không gian, cho hai đường thẳng phân biệt a, b và mặt phẳng (P). Những mệnh đề nào sau đây là đúng?

a) Nếu a và (P) có điểm chung thì a không song song với (P).

b) Nếu a và (P) có điểm chung thì a và (P) cắt nhau.

c) Nếu a song song với b và b nằm trong (P) thì a song song với (P).

d) Nếu a và b song song với (P) thì a song song với b.

Lời giải:

a) Mệnh đề a) là mệnh đề đúng vì nếu a và (P) có điểm chung thì a cắt (P) hoặc a nằm trong (P) nên a không song song với (P).

b) Mệnh đề b) là mệnh đề sai vì nếu a và (P) có điểm chung thì a và (P) cắt nhau hoặc a nằm trong (P).

c) Mệnh đề c) là mệnh đề sai vì a có thể nằm trong (P).

d) Mệnh đề d) là mệnh đề sai vì a và b có thể cắt nhau.

Lời giải bài tập Toán 11 Bài 12: Đường thẳng và mặt phẳng song song hay, chi tiết khác:

Bài 4.17 trang 87 Toán 11 Tập 1 - Kết nối tri thức

Giải Toán 11 Bài 12: Đường thẳng và mặt phẳng song song - Kết nối tri thức

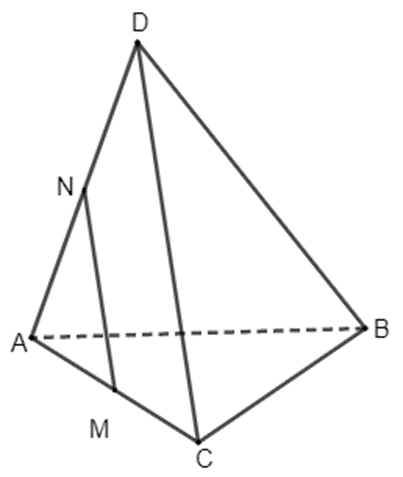
Bài 4.17 trang 87 Toán 11 Tập 1: Cho hai tam giác ABC và ABD không cùng nằm trong một mặt phẳng. Gọi M, N lần lượt là trung điểm của các cạnh AC, AD.

a) Đường thẳng AM có song song với mặt phẳng (BCD) hay không? Hãy giải thích tại sao.

b) Đường thẳng MN có song song với mặt phẳng (BCD) hay không? Hãy giải thích tại sao.

Lời giải:

a) Vì M là trung điểm của cạnh AC nên đường thẳng AM chứa điểm C.

Lại có điểm C thuộc mặt phẳng (BCD) và điểm A không thuộc mặt phẳng (BCD) (do bốn điểm A, B, C, D không đồng phẳng). Do đó, đường thẳng AM cắt mặt phẳng (BCD) tại điểm C. Vậy đường thẳng AM không song song với mặt phẳng (BCD).

b) Vì M, N lần lượt là trung điểm của các cạnh AC, AD nên MN là đường trung bình của tam giác ACD, suy ra MN // CD.

Lại có đường thẳng CD nằm trong mặt phẳng (BCD) và đường thẳng MN không nằm trong mặt phẳng (BCD).

Vậy đường thẳng MN song song với mặt phẳng (BCD).

Lời giải bài tập Toán 11 Bài 12: Đường thẳng và mặt phẳng song song hay, chi tiết khác:

Bài 4.18 trang 87 Toán 11 Tập 1 - Kết nối tri thức

Giải Toán 11 Bài 12: Đường thẳng và mặt phẳng song song - Kết nối tri thức

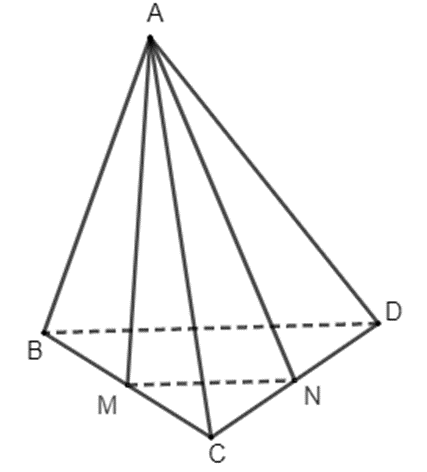
Bài 4.18 trang 87 Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của hai cạnh BC, CD. Chứng minh rằng đường thẳng BD song song với mặt phẳng (AMN).

Lời giải:

Vì M, N lần lượt là trung điểm của hai cạnh BC, CD nên MN là đường trung bình của tam giác BCD, suy ra MN // BD.

Mà đường thẳng MN nằm trong mặt phẳng (AMN).

Do đó, đường thẳng BD song song với mặt phẳng (AMN).

Lời giải bài tập Toán 11 Bài 12: Đường thẳng và mặt phẳng song song hay, chi tiết khác:

Bài 4.19 trang 87 Toán 11 Tập 1 - Kết nối tri thức

Giải Toán 11 Bài 12: Đường thẳng và mặt phẳng song song - Kết nối tri thức

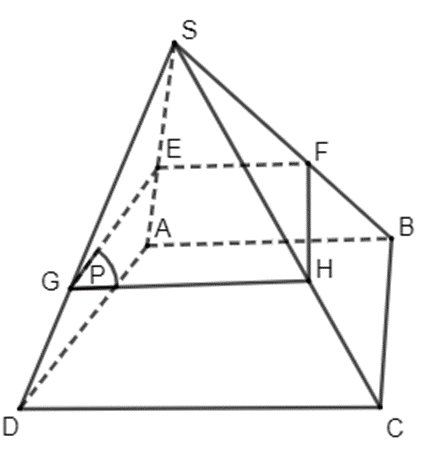
Bài 4.19 trang 87 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy là hình thang (AB // CD). Gọi E là một điểm nằm giữa S và A. Gọi (P) là mặt phẳng qua E và song song với hai đường thẳng AB, AD. Xác định giao tuyến của (P) và các mặt bên của hình chóp. Hình tạo bởi các giao tuyến là hình gì?

Lời giải:

+) Mặt phẳng (SAB) chứa đường thẳng AB song song với mặt phẳng (P) nên mặt phẳng (SAB) cắt mặt phẳng (P) theo giao tuyến song song với AB. Vẽ EF // AB (F thuộc SB) thì EF là giao tuyến của (P) và (SAB).

+) Mặt phẳng (SAD) chứa đường thẳng AD song song với mặt phẳng (P) nên mặt phẳng (SAD) cắt mặt phẳng (P) theo giao tuyến song song với AD. Vẽ EG // AD (G thuộc SD) thì EG là giao tuyến của (P) và (SAD).

+) Trong mặt phẳng (SCD), qua G vẽ đường thẳng song song với CD cắt SC tại H.

Ta có: GH // CD và CD // AB nên GH // AB, do đó GH nằm trong mặt phẳng (P).

Vì G thuộc SD nên G thuộc mặt phẳng (SCD) và H thuộc SC nên H thuộc mặt phẳng (SCD), do đó GH nằm trong mặt phẳng (SCD).

Vậy GH là giao tuyến của (P) và (SCD).

+) Nối H với F, ta có H thuộc SC nên H thuộc mặt phẳng (SBC). Vì F thuộc SB nên F thuộc mặt phẳng (SBC). Do đó, HF nằm trong mặt phẳng (SBC).

Lại có H và F đều thuộc (P) nên HF nằm trong mặt phẳng (P).

Vậy HF là giao tuyến của (P) và (SBC).

+) Ta có: EF // AB và GH // AB nên EF // GH, do vậy tứ giác EFHG là hình thang.

Lời giải bài tập Toán 11 Bài 12: Đường thẳng và mặt phẳng song song hay, chi tiết khác:

Bài 4.20 trang 87 Toán 11 Tập 1 - Kết nối tri thức

Giải Toán 11 Bài 12: Đường thẳng và mặt phẳng song song - Kết nối tri thức

Bài 4.20 trang 87 Toán 11 Tập 1: Bạn Nam quan sát thấy dù cửa ra vào được mở ở vị trí nào thì mép trên của cửa luôn song song với một mặt phẳng cố định. Hãy cho biết đó là mặt phẳng nào và giải thích tại sao.

Lời giải:

Cánh cửa có dạng hình chữ nhật nên mép trên cửa song song với mép dưới cửa. Mà mép dưới của cửa luôn tạo với mặt sàn một đường thẳng, do đó mép trên của cửa luôn song song với mặt sàn nhà.

Lời giải bài tập Toán 11 Bài 12: Đường thẳng và mặt phẳng song song hay, chi tiết khác:

SBT Toán 11 Kết nối tri thức Bài 12: Đường thẳng và mặt phẳng song song

Với giải sách bài tập Toán 11 Bài 12: Đường thẳng và mặt phẳng song song sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 11 Bài 12.

Giải SBT Toán 11 Kết nối tri thức Bài 12: Đường thẳng và mặt phẳng song song

Đường thẳng và mặt phẳng song song (Lý thuyết Toán lớp 11) | Kết nối tri thức

Với tóm tắt lý thuyết Toán 11 Bài 12: Đường thẳng và mặt phẳng song song sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 11 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 11.

Đường thẳng và mặt phẳng song song (Lý thuyết Toán lớp 11) | Kết nối tri thức

Lý thuyết Đường thẳng và mặt phẳng song song

1. Đường thẳng song song với mặt phẳng

Cho đường thẳng d và mặt phẳng (α). Nếu d và (α) không có điểm chung thì ta nói d song song với (α) hay (α) song song với d và kí hiệu là d // (α) hay (α) // d.

Ngoài ra:

- Nếu d và (α) có một điểm chung duy nhất M thì ta nói d và (α) cắt nhau tại điểm M và kí hiệu d ∩ (α) = {M} hay d ∩ (α) = M.

- Nếu d và (α) có nhiều hơn một điểm chung thì ta nói d nằm trong (α) hay (α) chứa d và kí hiệu d ⸦ (α) hay (α) ⸧ d.

Ví dụ: Cho hình chóp tam giác S.ABC. Trong các mặt phẳng chứa các mặt của hình chóp, hãy cho biết:

a) Đường thẳng SA cắt các mặt phẳng nào?

b) Đường thẳng SA nằm trong mặt phẳng nào?

Hướng dẫn giải

a) Đường thẳng SA cắt các mặt phẳng (SBC) và (ABC).

Vì SA ∩ (SBC) = {S}; SA ∩ (ABC) ={A}

b) Đường thẳng SA nằm trong mặt phẳng (SAB) và (SAC).

2. Điều kiện và tính chất của đường thẳng song song với mặt phẳng

- Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong (P) thì a song song với (P).

- Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì b song song với a.

Chú ý: Cho hai đường thẳng chéo nhau thì có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.

Ví dụ: Cho hình chóp S.ABCD có đáy là hình thang (AB // CD). Hai đường thẳng SC và AB có chéo nhau không? Chứng minh rằng AB // (SCD).

Ta có: SC và AB chéo nhau.

Vì AB và SC chéo nhau nên AB không nằm trong (SCD).

Vì AB // CD (theo giả thiết) nên AB // (SCD).

Bài tập Đường thẳng và mặt phẳng song song

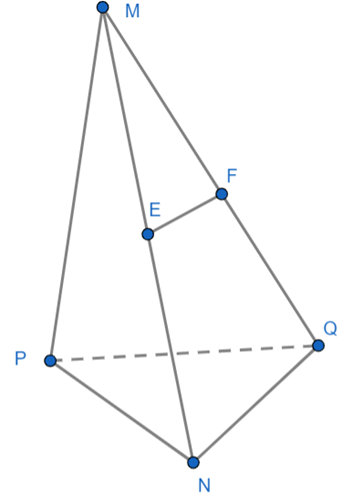
Bài 1: Cho hai tam giác MNP và MNQ không cùng nằm trong một mặt phẳng. Gọi E, F lần lượt là trung điểm của các cạnh MN, MQ.

a) Đường thẳng ME có song song với mặt phẳng (NPQ) không?

b) Đường thẳng EF có song song với mặt phẳng (NPQ) không?

Hướng dẫn giải

a) ME cắt (NPQ) tại N nên ME không song song với (NPQ).

b) Ta thấy: EF là đường trung bình của tam giác MNQ nên EF // NQ.

Ta có: 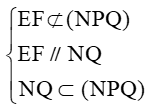nên EF // (NPQ).

Bài 2: Cho tứ diện ABCD. Gọi P, Q lần lượt là trung điểm của hai cạnh BC, CD. Chứng minh rằng BD // (APQ).

Hướng dẫn giải

Ta có: P, Q lần lượt là trung điểm của BC và CD nên PQ là đường trung bình của tam giác BCD. Suy ra PQ // BD.

Ta có: nên BD // (APQ).

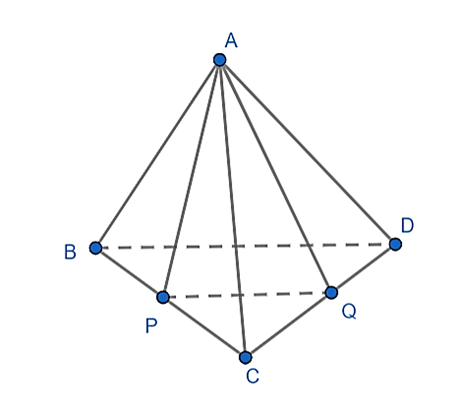
Bài 3: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm các cạnh AB và CD.

a) Chứng minh MN // (SBC), MN // (SAD).

b) Gọi P là trung điểm cạnh SA. Chứng minh SB và SC đều song song với (MNP).

Hướng dẫn giải

a) Vì M, N lần lượt là trung điểm của AB, CD nên MN là đường trung bình của hình thang ABCD (hình bình hành cũng là hình thang).

Suy ra MN // BC và MN // AD.

Ta có:

, suy ra MN // (SBC)

, suy ra MN // (SAD)

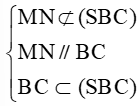
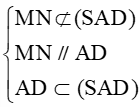
b) Ta có : P là điểm chung của (MNP) và (SAD).

Mà MN // AD

Do đó giao tuyến của (MNP) và (SAD) là đường thẳng qua P song song với AD và MN và đường thẳng này cắt SD tại Q.

Suy ra: PQ = (MNP) ∩ (SAD)

Xét $∆$SAD, ta có: PQ // AD

Mà P là trung điểm SA

Suy ra: Q là trung điểm SD.

Khi đó, QN là đường trung bình của $∆$SCD.

Suy ra QN // SC.

Ta có : 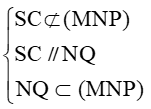nên SC // (MNP).

Lại có M và P lần lượt là trung điểm của AB và SA nên MP là đường trung bình của tam giác SAB, suy ra MP // SB.

Ta có: nên SB // (MNP).

Học tốt Đường thẳng và mặt phẳng song song

Các bài học để học tốt Đường thẳng và mặt phẳng song song Toán lớp 11 hay khác:

12 Bài tập Đường thẳng và mặt phẳng song song (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 11

Với 12 bài tập trắc nghiệm Đường thẳng và mặt phẳng song song Toán lớp 11 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 11.

12 Bài tập Đường thẳng và mặt phẳng song song (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 11

Nội dung đang được cập nhật ...

Xem thêm bài tập trắc nghiệm Toán lớp 11 Kết nối tri thức có đáp án hay khác: