Với giải bài tập Toán 7 Bài 22: Đại lượng tỉ lệ thuận sách Kết nối tri thức hay nhất, chi tiết giúp học sinh lớp 7 dễ dàng làm bài tập Toán 7 Bài 22.

Giải Toán 7 Kết nối tri thức Bài 22: Đại lượng tỉ lệ thuận

Video Giải Toán 7 Bài 22: Đại lượng tỉ lệ thuận - Cô Trần Thị Ngọc Anh (Giáo viên VietJack)

Mở đầu

Giải Toán 7 trang 11 Tập 2

Mở đầu trang 11 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 22: Đại lượng tỉ lệ thuận

Mở đầu trang 11 Toán 7 Tập 2: Bột sắn dây được làm từ củ sắn dây, là một loại thực phẩm có nhiều tác dụng tốt với sức khỏe. Ông An nhận thấy cứ 4,5 kg củ sắn dây tươi thì thu được khoảng 1 kg bột. Hỏi với 3 tạ củ sắn dây tươi, ông An sẽ thu được khoảng bao nhiêu kilôgam bột sắn dây?

Lời giải:

Đổi 3 tạ = 300 kg.

Ông An thu được số kilôgam bột sắn dây là:

$\frac{300}{4,5}.1=\frac{3000}{45}=\frac{3000:15}{45:15}=\frac{200}{3}$≈ 66,7 kg.

Vậy với 3 tạ củ sắn dây tươi, ông An thu được khoảng 66,7 kg bột sắn dây.

Lời giải bài tập Toán 7 Bài 22: Đại lượng tỉ lệ thuận hay, chi tiết khác:

HĐ1 trang 11 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 22: Đại lượng tỉ lệ thuận

HĐ1 trang 11 Toán 7 Tập 2: Một xe ô tô di chuyển với vận tốc không đổi 60 km/h. Gọi s (km) là quãng đường ô tô đi được trong khoảng thời gian t (h)

Thay mỗi dấu “?” trong bảng sau bằng số thích hợp:

Lời giải:

Ta đã biết quãng đường vật đi được bằng thời gian vật di chuyển nhân với vận tốc.

Do đó với t = 1 thì s = 60.1 = 60 km.

Với t = 1,5 thì s = 60.1,5 = 90 km.

Với t = 2 thì s = 60.2 = 120 km.

Với t = 3 thì s = 60.3 = 180 km.

Ta có bảng sau:

Lời giải bài tập Toán 7 Bài 22: Đại lượng tỉ lệ thuận hay, chi tiết khác:

HĐ2 trang 11 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 22: Đại lượng tỉ lệ thuận

HĐ2 trang 11 Toán 7 Tập 2: Một xe ô tô di chuyển với vận tốc không đổi 60 km/h. Gọi s (km) là quãng đường ô tô đi được trong khoảng thời gian t (h)

Viết công thức tính quãng đường s theo thời gian di chuyển tương ứng t.

Lời giải:

Công thức tính quãng đường s theo thời gian di chuyển tương ứng t là:

s = 60t.

Lời giải bài tập Toán 7 Bài 22: Đại lượng tỉ lệ thuận hay, chi tiết khác:

Câu hỏi trang 11 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 22: Đại lượng tỉ lệ thuận

Câu hỏi trang 11 Toán 7 Tập 2: Trong Hoạt động 2, quãng đường s có tỉ lệ thuận với thời gian t không? Thời gian t có tỉ lệ thuận với quãng đường s không?

Lời giải:

Trong Hoạt động 2, do s = 60t nên quãng đường s tỉ lệ thuận với thời gian t.

Do s = 60t nên t = $\frac{s}{60}=\frac{1}{60}.s$

Do đó thời gian t tỉ lệ thuận với quãng đường s.

Lời giải bài tập Toán 7 Bài 22: Đại lượng tỉ lệ thuận hay, chi tiết khác:

Luyện tập 1 trang 12 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 22: Đại lượng tỉ lệ thuận

Luyện tập 1 trang 12 Toán 7 Tập 2: Theo Viện Dinh dưỡng Quốc gia, cứ trong 100 g đậu tương (đậu nành) thì có 34 g protein. Khối lượng protein trong đậu tương có tỉ lệ thuận với khối lượng đậu tương không? Nếu có thì hệ số tỉ lệ là bao nhiêu?

Lời giải:

Do cứ trong 100 g đậu tương thì có 34 g protein nên khối lượng protein trong đậu tương tỉ lệ thuận với khối lượng đậu tương.

Hệ số tỉ lệ bằng: 34 : 100 = $\frac{34}{100}=\frac{17}{50}$.

Lời giải bài tập Toán 7 Bài 22: Đại lượng tỉ lệ thuận hay, chi tiết khác:

Vận dụng trang 12 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 22: Đại lượng tỉ lệ thuận

Vận dụng trang 12 Toán 7 Tập 2: Em hãy giải bài toán mở đầu

Lời giải:

Đổi 3 tạ = 300 kg.

Gọi x là số kilôgam bột sắn dây ông An thu hoạch được từ 3 tạ củ (x > 0).

Số kilôgam củ sắn dây tươi và số kilôgam bột sắn dây thu được là hai đại lượng tỉ lệ thuận nên $\frac{4,5}{1}=\frac{300}{x}$

Suy ra 4,5x = 300.

Do đó x = 300 : 4,5 = $\frac{3000}{45}=\frac{200}{3}$ ≈ 66,7 kg (thỏa mãn).

Vậy với 3 tạ củ sắn dây tươi, ông An thu được khoảng 66,7 kg bột sắn dây.

Lời giải bài tập Toán 7 Bài 22: Đại lượng tỉ lệ thuận hay, chi tiết khác:

Luyện tập 2 trang 13 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 22: Đại lượng tỉ lệ thuận

Luyện tập 2 trang 13 Toán 7 Tập 2: Hai thanh kim loại đồng chất có thể tích tương ứng là 10 cm³ và 15 cm³. Hỏi mỗi thanh nặng bao nhiêu gam, biết rằng một thanh nặng hơn thanh kia 40 g?

Lời giải:

Gọi khối lượng hai thanh kim loại có thể tích 10 cm³ và 15 cm³ lần lượt là x và y gam (x > 0, y > 0).

Do 10 < 15 nên x < y.

Mà một thanh nặng hơn thanh kia 40 g nên y - x = 40.

Do khối lượng của một vật đồng chất tỉ lệ thuận với thể tích của nó nên $\frac{x}{10}=\frac{y}{15}$.

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\frac{x}{10}=\frac{y}{15}=\frac{y-x}{15-10}=\frac{40}{5}$ = 8.

Do đó x = 10.8 = 80, y = 15.8 = 120.

Vậy khối lượng hai thanh kim loại có thể tích 10 cm³ và 15 cm³ lần lượt là 80 g và 120 g.

Lời giải bài tập Toán 7 Bài 22: Đại lượng tỉ lệ thuận hay, chi tiết khác:

Luyện tập 3 trang 14 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 22: Đại lượng tỉ lệ thuận

Luyện tập 3 trang 14 Toán 7 Tập 2: Hãy chia 1 tấn gạo thành ba phần có khối lượng tỉ lệ thuận với 2; 3; 5

Lời giải:

Đổi 1 tấn = 10 tạ.

Gọi số gạo của ba phần chia lần lượt là x, y, z tạ (x > 0, y > 0, z > 0).

Theo đề bài ta có: x + y + z =10 và $\frac{x}{2}=\frac{y}{3}=\frac{z}{5}$

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\frac{x}{2}=\frac{y}{3}=\frac{z}{5}=\frac{x+y+z}{2+3+5}=\frac{10}{10}$ = 1.

Do đó x = 2.1 = 2, y = 3.1 = 3, z = 5.1 = 5.

Vậy số gạo chia làm ba phần có khối lượng lần lượt là 2 tạ, 3 tạ và 5 tạ.

Lời giải bài tập Toán 7 Bài 22: Đại lượng tỉ lệ thuận hay, chi tiết khác:

Bài 6.17 trang 14 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 22: Đại lượng tỉ lệ thuận

Bài 6.17 trang 14 Toán 7 Tập 2: Cho biết x và y là hai đại lượng tỉ lệ thuận. Thay mỗi dấu “?” trong bảng sau bằng số thích hợp

Viết công thức mô tả mối quan hệ phụ thuộc giữa hai đại lượng x và y.

Lời giải:

Với y = -6, x = 2 ta có $\frac{y}{x}=\frac{-6}{2}$ = -3.

Do x và y là hai đại lượng tỉ lệ thuận nên hệ số tỉ lệ là -3, tức y = -3x.

Với x = 4 thì y = 4.(-3) = -12.

Với x = 5 thì y = 5.(-3) = -15.

Với y = 9 thì 9 = -3x do đó x = 9 : (-3) = -3.

Với y = 18 thì 18 = -3x do đó x = 18 : (-3) = -6.

Với y = 1,5 thì 1,5 = -3x do đó x = 1,5 : (-3) = -0,5.

Ta có bảng sau:

Lời giải bài tập Toán 7 Bài 22: Đại lượng tỉ lệ thuận hay, chi tiết khác:

Bài 6.18 trang 14 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 22: Đại lượng tỉ lệ thuận

Bài 6.18 trang 14 Toán 7 Tập 2: Theo bảng giá trị dưới đây, hai đại lượng x và y có phải là hai đại lượng tỉ lệ thuận không?

a)

b)

Lời giải:

a) Ta thấy $\frac{y}{x}=\frac{15}{5}$= 3; $\frac{y}{x}=\frac{27}{9}$= 3; $\frac{y}{x}=\frac{45}{15}$= 3; $\frac{y}{x}=\frac{72}{24}$= 3.

Do đó $\frac{y}{x}=3$ hay y = 3x.

Vậy x và y là hai đại lượng tỉ lệ thuận.

b) Ta thấy $\frac{y}{x}=\frac{8}{4}$ = 2; $\frac{y}{x}=\frac{16}{8}$ = 2; $\frac{y}{x}=\frac{30}{16}=\frac{15}{8}$; $\frac{y}{x}=\frac{50}{25}$= 2.

Do $\frac{15}{8}$ ≠ 2 nên x và y không phải hai đại lượng tỉ lệ thuận.

Lời giải bài tập Toán 7 Bài 22: Đại lượng tỉ lệ thuận hay, chi tiết khác:

Bài 6.19 trang 14 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 22: Đại lượng tỉ lệ thuận

Bài 6.19 trang 14 Toán 7 Tập 2: Cho biết y tỉ lệ thuận với x theo hệ số tỉ lệ a, x tỉ lệ thuận với z theo hệ số tỉ lệ b. Hỏi y có tỉ lệ thuận với z không? Nếu có thì hệ số tỉ lệ là bao nhiêu?

Lời giải:

y tỉ lệ thuận với x theo hệ số tỉ lệ a nên y = ax.

x tỉ lệ thuận với z theo hệ số tỉ lệ b nên x = bz.

Khi đó y = ax = abz.

Vậy y tỉ lệ thuận với z với hệ số tỉ lệ là ab.

Lời giải bài tập Toán 7 Bài 22: Đại lượng tỉ lệ thuận hay, chi tiết khác:

Bài 6.20 trang 14 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 22: Đại lượng tỉ lệ thuận

Bài 6.20 trang 14 Toán 7 Tập 2: Hai bể nước hình hộp chữ nhật có chiều dài và chiều rộng tương ứng bằng nhau, nhưng chiều cao của bể thứ nhất bằng $\frac{3}{4}$ chiều cao của bể thứ hai (nếu dùng máy bơm có cùng công suất).

Lời giải:

Gọi thời gian để bơm đầy nước vào bể thứ hai là x giờ (x > 0).

Chiều cao của bể nước và thời gian bơm nước đầy bể là hai đại lượng tỉ lệ thuận với nhau nên $\frac{4,5}{x}=\frac{3}{4}$.

Suy ra 3x = 4,5 . 4 = 18.

Do đó x = 18 : 3 = 6 giờ (thỏa mãn).

Vậy mất 6 giờ để bơm đầy nước vào bể thứ hai.

Lời giải bài tập Toán 7 Bài 22: Đại lượng tỉ lệ thuận hay, chi tiết khác:

Bài 6.21 trang 14 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 22: Đại lượng tỉ lệ thuận

Bài 6.21 trang 14 Toán 7 Tập 2: Để chuẩn bị cho học sinh làm thí nghiệm, cô Hương chia 1,5 lít hóa chất thành ba phần tỉ lệ thuận với 4; 5; 6 và đựng trong ba chiếc lọ. Hỏi mỗi chiếc lọ đựng bao nhiêu lít hóa chất đó?

Lời giải:

Gọi số lít hóa chất ba lọ đựng được lần lượt là x, y, z lít (x > 0, y > 0, z > 0).

Theo đề bài ta có x + y + z = 1,5 và $\frac{x}{4}=\frac{y}{5}=\frac{z}{6}$.

Áp dụng tính chất của dãy tỉ số bằng nhau ta có $\frac{x}{4}=\frac{y}{5}=\frac{z}{6}=\frac{x+y+z}{4+5+6}=\frac{1,5}{15}$= 0,1.

Do đó x = 4.0,1 = 0,4; y = 5.0,1 = 0,5; z = 6.0,1 = 0,6.

Vậy số lít hóa chất ba lọ đựng được lần lượt là 0,4 lít; 0,5 lít và 0,6 lít.

Lời giải bài tập Toán 7 Bài 22: Đại lượng tỉ lệ thuận hay, chi tiết khác:

Sách bài tập Toán 7 Bài 22: Đại lượng tỉ lệ thuận - Kết nối tri thức

Với giải sách bài tập Toán 7 Bài 22: Đại lượng tỉ lệ thuận sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Bài 22.

Giải SBT Toán 7 Bài 22: Đại lượng tỉ lệ thuận - Kết nối tri thức

Giải SBT Toán 7 trang 10 Tập 2

Vở thực hành Toán 7 Bài 22: Đại lượng tỉ lệ thuận - Kết nối tri thức

Với giải vở thực hành Toán lớp 7 Bài 22: Đại lượng tỉ lệ thuận sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập về nhà trong VTH Toán 7 Bài 22.

Giải vở thực hành Toán 7 Bài 22: Đại lượng tỉ lệ thuận - Kết nối tri thức

B – CÂU HỎI TRẮC NGHIỆM

Giải VTH Toán 7 trang 14 Tập 2

Đại lượng tỉ lệ thuận (Lý thuyết Toán lớp 7) - Kết nối tri thức

Với tóm tắt lý thuyết Toán 7 Bài 22: Đại lượng tỉ lệ thuận sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Đại lượng tỉ lệ thuận (Lý thuyết Toán lớp 7) - Kết nối tri thức

Lý thuyết Đại lượng tỉ lệ thuận

1. Đại lượng tỉ lệ thuận

• Nếu đại lượng y liên hệ với đại lượng x theo công thức y = ax (a là hằng số khác 0) thì ta nói y tỉ lệ thuận với x theo hệ số tỉ lệ a.

Chú ý:

Nếu y tỉ lệ thuận với x theo hệ số tỉ lệ a thì x tỉ lệ thuận với y theo hệ số tỉ lệ $\frac{1}{a}$. Khi đó ta nói x và y là hai đại lượng tỉ lệ thuận.

Ví dụ: Nếu y = 5x thì y tỉ lệ thuận với x theo hệ số 5, hay x tỉ lệ thuận với y theo hệ số $\frac{1}{5}$ .

Nhận xét:

Nếu đại lượng y tỉ lệ thuận với đại lượng x thì:

• Tỉ số hai giá trị tương ứng của chúng luôn không đổi (và bằng hệ số tỉ lệ):

$\frac{y_1}{x_1}=\frac{y_2}{x_2}=\frac{y_3}{x_3}=\mathrm{...}=a$

• Tỉ số hai giá trị bất kì của đại lượng này bằng tỉ số hai giá trị tương ứng của đại lượng kia:

$\frac{y_1}{y_2}=\frac{x_1}{x_2};\frac{y_1}{y_3}=\frac{x_1}{x_3};\frac{y_2}{y_3}=\frac{x_2}{x_3};\mathrm{...}$

Ví dụ: Cho biết x và y là hai đại lượng tỉ lệ thuận. Điền số thích hợp vào ô trống trong bảng sau:

Hướng dẫn giải:

Ta có: x và y là hai đại lượng tỉ lệ thuận nên y = a . x

Khi x = 2 thì y = -4 nên ta có $a=\frac{y}{x}=\frac{-4}{2}=-2$

Vậy y tỉ lệ thuận với x theo tỉ số -2, hay y = -2 . x

Từ đó:

Với x = -3 thì y = (-2).(-3) = 6

Với x = -1 thì y = (-2).(-1) =2

Với x = 1 thì y = (-2).1 = -2

Với x= 5 thì y = (-2).5 = -10

Vậy ta có bảng sau:

2. Một số bài toán về đại lượng tỉ lệ thuận

Để giải toán về đại lượng tỉ lệ thuận, ta cần nhận biết hai đại lượng tỉ lệ thuận trong bài toán. Từ đó ta có thể lập các tỉ số bằng nhau và dựa vào tính chất của dãy tỉ số bằng nhau để tìm các yếu tố chưa biết.

Ví dụ:

Học sinh của ba lớp 7 cần phải trồng và chăm sóc 24 cây xanh. Lớp 7A có 32 học sinh, lớp 7B có 28 học sinh, lớp 7C có 36 học sinh. Hỏi mỗi lớp phải trồng và chăm sóc bao nhiêu cây xanh biết rằng số cây xanh tỉ lệ với số học sinh?

Hướng dẫn giải:

Gọi số cây trồng của các lớp 7A, 7B, 7C lần lượt là x, y, z (cây) (x; y; z $\in {\mathbb{N}}^{*}$; x; y; z < 24)

Số cây xanh tỉ lệ với số học sinh nghĩa là x : y : z = 32 : 28 : 36, hay $\frac{x}{32}=\frac{y}{28}=\frac{z}{36}$

Tổng số cây xanh phải chăm sóc là 24 cây nghĩa là x + y + z = 24.

Theo tính chất của dãy tỉ số bằng nhau ta có:

$\frac{x}{32}=\frac{y}{28}=\frac{z}{36}=\frac{x+y+z}{32+28+36}=\frac{24}{96}=\frac{1}{4}$

Vậy:

$\frac{x}{32}=\frac{1}{4}\Rightarrow x=32.\frac{1}{4}=8$

$\frac{y}{28}=\frac{1}{4}\Rightarrow y=28.\frac{1}{4}=7$

$\frac{z}{36}=\frac{1}{4}\Rightarrow z=36.\frac{1}{4}=9$

Vậy số cây trồng của các lớp 7A, 7B, 7C theo thứ tự là 8, 7, 9 (cây).

Bài tập Đại lượng tỉ lệ thuận

Bài 1. Cho biết y tỉ lệ thuận với x theo hệ số tỉ lệ a = $-\frac{3}{5}$. Hỏi x tỉ lệ thuận với y theo hệ số tỉ lệ nào?

Hướng dẫn giải:

Ta có y tỉ lệ thuận với x theo hệ số tỉ lệ a = $-\frac{3}{5}$⇒ y = $-\frac{3}{5}$. x

⇒ x = $-\frac{5}{3}$ . y Hay x tỉ lệ thuận với y theo hệ số tỉ lệ là $-\frac{5}{3}$ .

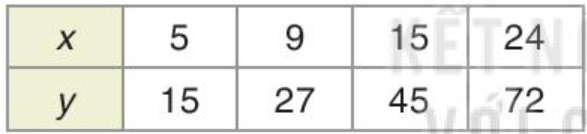
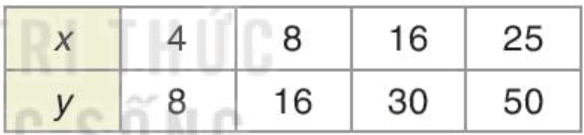
Bài 2. Hai đại lượng x và y có tỉ lệ thuận với nhau hay không nếu:

a)

b)

Hướng dẫn giải:

a) Ta có:

$\frac{x}{y}=\frac{1}{9}=\frac{2}{18}=\frac{3}{27}=\frac{4}{36}=\frac{5}{45}$

⇒ y = 9x

Vậy x và y là hai đại lượng tỉ lệ thuận.

b) Ta có:

$\frac{1}{12}=\frac{2}{24}=\frac{5}{60}=\frac{6}{72}\ne \frac{9}{90}$

Do đó, hai đại lượng x và y không tỉ lệ thuận với nhau.

Bài 3. Gọi x, y, z theo thứ tự là số vòng quay của kim giờ, kim phút và kim giây trong cùng một thời gian. Tìm hệ số tỉ lệ của z đối với x.

Hướng dẫn giải:

Trên đồng hồ có 12 số chia mặt đồng hồ thành 12 khoảng bằng nhau.

Khi kim phút quay được một vòng thì kim giờ quay được một khoảng. Do đó, khi kim phút quay được 12 vòng thì kim giờ quay được một vòng.

Vậy y tỉ lệ thuận với x theo hệ số tỉ lệ là 12 tức là y = 12x.

Khi kim giây quay được 60 vòng thì kim phút quay được một vòng. Do đó, z tỉ lệ thuận với y theo hệ số tỉ lệ là 60 tức là z = 60y.

Suy ra, z = 60y = 60 . 12x = 720x

Vậy z tỉ lệ thuận với x theo hệ số tỉ lệ là 720.

Bài 4. Hạnh và Vân định làm mứt dẻo từ 2,5kg dâu. Theo công thức, cứ 2kg dâu thì cần 3kg đường. Hạnh bảo cần 3,75kg đường còn Vân bảo cần 3,25kg. Theo em ai đúng và vì sao?

Hướng dẫn giải:

Gọi khối lượng đường là y (kg), khối lượng dâu là x (kg). (x, y > 0)

Vì khối lượng đường tỉ lệ thuận với khối lượng dâu nên ta có y = ax

Theo điều kiện đề bài x = 2 thì y = 3 suy ra 3 = a . 2 hay $a=\frac{3}{2}$.

Do đó: $y=\frac{3}{2}x$

Khi x = 2,5kg thì $y=\frac{3}{2}.2,5=3,75$(kg).

Vậy khi làm 2,5kg dâu thì cần 3,75kg đường, tức là Hạnh nói đúng.

Học tốt Đại lượng tỉ lệ thuận

Các bài học để học tốt Đại lượng tỉ lệ thuận Toán lớp 7 hay khác:

15 Bài tập Đại lượng tỉ lệ thuận (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 7

Với 15 bài tập trắc nghiệm Đại lượng tỉ lệ thuận Toán lớp 7 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 7.

15 Bài tập Đại lượng tỉ lệ thuận (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 7

Xem thử

Chỉ 150k mua trọn bộ trắc nghiệm Toán 7 Kết nối tri thức (cả năm) có lời giải chi tiết, bản word trình bày đẹp mắt, dễ dàng chỉnh sửa: