Với giải bài tập Toán 7 Bài 27: Phép nhân đa thức một biến sách Kết nối tri thức hay nhất, chi tiết giúp học sinh lớp 7 dễ dàng làm bài tập Toán 7 Bài 27.

Giải Toán 7 Kết nối tri thức Bài 27: Phép nhân đa thức một biến

Video Giải Toán 7 Bài 27: Phép nhân đa thức một biến - Cô Nguyễn Ngọc (Giáo viên VietJack)

Mở đầu

Giải Toán 7 trang 36 Tập 2

Mở đầu trang 36 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 27: Phép nhân đa thức một biến

Mở đầu trang 36 Toán 7 Tập 2:

Anh Pi: Em hãy:

- Lấy tuổi của mình cộng với 1 rồi bình phương lên. Số nhận được gọi là kết quả thứ nhất.

- Lại lấy tuổi của mình trừ đi 1 rồi bình phương lên. Số nhận được gọi là kết quả thứ hai.

- Lấy kết quả thứ nhất trừ đi kết quả thứ hai và cho anh biết kết quả cuối cùng.

Anh sẽ đoán được tuổi của em.

Không biết anh Pi làm thế nào nhỉ? Học xong bài này em sẽ khám phá được bí mật đó.

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

Lời giải:

Giả sử kết quả cuối cùng là 48.

Gọi tuổi cần đoán là x tuổi (x $\in \mathbb{N}*$).

Lấy tuổi cộng 1 rồi bình phương lên ta được (x + 1)².

Ta có (x + 1)² = (x + 1).(x + 1) = x.(x + 1) + 1.(x + 1)

= x.x + x.1 + 1.x + 1.1

= x¹⁺¹ + x + x + 1

= x² + 2x + 1

Lấy tuổi trừ 1 rồi bình phương lên ta được (x - 1)².

Ta có (x - 1)² = (x - 1).(x - 1) = x.(x - 1) - 1.(x - 1)

= x[x + (-1)] - (x - 1)

= x.x + x.(-1) - x + 1

= x¹⁺¹ + (-x) - x + 1

= x² - x - x + 1

= x² - 2x + 1

Lấy kết quả thứ nhất trừ đi kết quả thứ hai ta được:

(x² + 2x + 1) - (x² - 2x + 1)

= x² + 2x + 1 - x² + 2x - 1

= (x² - x²) + (2x + 2x) + (1 - 1)

= 4x

Do kết quả cuối cùng là 48 nên 4x = 48

x = 48 : 4

x = 12.

Vậy tuổi cần đoán là 12.

Lời giải bài tập Toán 7 Bài 27: Phép nhân đa thức một biến hay, chi tiết khác:

HĐ1 trang 36 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 27: Phép nhân đa thức một biến

HĐ1 trang 36 Toán 7 Tập 2:

Hãy nhắc lại cách nhân hai đơn thức và tính (12x³) . (-5x²).

Lời giải:

Cách nhân hai đơn thức: Để nhân hai đơn thức tùy ý, ta thực hiện nhân hai hệ số với nhau và nhân hai lũy thừa của biến với nhau.

(12x³) . (-5x²) = [12 . (-5)] . (x³ . x²) = -60.(x^{3 + 2}) = -60x⁵.

Lời giải bài tập Toán 7 Bài 27: Phép nhân đa thức một biến hay, chi tiết khác:

HĐ2 trang 36 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 27: Phép nhân đa thức một biến

HĐ2 trang 36 Toán 7 Tập 2: Áp dụng tính chất phân phối của phép nhân đối với phép cộng, hãy tìm tích 2x . (3x² - 8x + 1). bằng cách nhân 2x với từng hạng tử của đa thức 3x² - 8x + 1 rồi cộng các tích tìm được.

Lời giải:

3x² - 8x + 1 = 3x² + (-8x) + 1.

Nhân 2x với 3x² ta được 2x . 3x² = (2 . 3) . (x . x²) = 6.x¹⁺² = 6x³.

Nhân 2x với -8x ta được: 2x . (-8x) = [2.(-8)] . (x . x) = -16x¹⁺¹ = -16x².

Nhân 2x với 1 ta được: 2x.1 = 2x.

Cộng các tích ta được 6x³ + (-16x²) + 2x = 6x³ - 16x² + 2x.

Lời giải bài tập Toán 7 Bài 27: Phép nhân đa thức một biến hay, chi tiết khác:

Luyện tập 1 trang 36 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 27: Phép nhân đa thức một biến

Luyện tập 1 trang 36 Toán 7 Tập 2: Tính (-2x²) . (3x - 4x³ + 7 - x²)

Lời giải:

(-2x²) . (3x - 4x³ + 7 - x²)

= (-2x²).3x + (-2x²).(-4x³) + (-2x²).7 + (-2x²).(-x²)

= [(-2).3] . (x².x) + [(-2).(-4)](x².x³) + [(-2).7]x² + [(-2).(-1)](x².x²)

= -6x³ + 8x⁵ + (-14x²) + 2x⁴

= -6x³ + 8x⁵ - 14x² + 2x⁴.

Lời giải bài tập Toán 7 Bài 27: Phép nhân đa thức một biến hay, chi tiết khác:

Vận dụng 1 trang 37 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 27: Phép nhân đa thức một biến

Vận dụng 1 trang 37 Toán 7 Tập 2:

a) Rút gọn biểu thức P(x) = 7x²(x² - 5x + 2) - 5x(x³ - 7x² + 3x).

b) Tính giá trị của biểu thức P(x) khi x = $-\frac{1}{2}$

Lời giải:

a) P(x) = 7x²(x² - 5x + 2) - 5x(x³ - 7x² + 3x)

P(x) = 7x².x² + 7x².(-5x) + 7x².2 + (-5x).x³ + (-5x).(-7x²) + (-5x).3x

P(x) = 7x⁴ + 7.(-5).(x².x) + 7.2x² + (-5x.x³) + [(-5).(-7)].(x.x²) + [(-5).3](x.x)

P(x) = 7x⁴ + (-35 x³) + 14x² + (-5x⁴) + 35x³ + (-15x²)

P(x) = 7x⁴ - 35x³ + 14x² - 5x⁴ + 35x³ - 15x²

P(x) = (7x⁴ - 5x⁴) + (- 35x³ + 35x³) + (14x² - 15x²)

P(x) = 2x⁴ + (-x²)

P(x) = 2x⁴ - x²

b) Thay x = $-\frac{1}{2}$vào biểu thức P(x) ta được:

P$(-\frac{1}{2})$= 2. ${(-\frac{1}{2})}^4$- ${(-\frac{1}{2})}^2$= 2. $\frac{{(-1)}^4}{2^4}$- $\frac{{(-1)}^2}{2^2}$= 2. $\frac{1}{16}$- $\frac{1}{4}$= $\frac{1}{8}-\frac{2}{8}$= $-\frac{1}{8}$.

Vậy P(x) = $-\frac{1}{8}$khi x = $-\frac{1}{2}$.

Lời giải bài tập Toán 7 Bài 27: Phép nhân đa thức một biến hay, chi tiết khác:

Thử thách nhỏ trang 37 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 27: Phép nhân đa thức một biến

Thử thách nhỏ trang 37 Toán 7 Tập 2:

Rút gọn biểu thức x³(x + 2) - x(x³ + 2³) - 2x(x² - 2²).

Lời giải:

x³(x + 2) - x(x³ + 2³) - 2x(x² - 2²)

= x³.x + x³.2 + (-x).x³ + (-x).2³ + (-2x).x² + (-2x).(-2²)

= x⁴ + 2x³ + (-x⁴) + (-x).8 + (-2x³) + (-2x).(-4)

= x⁴ + 2x³ - x⁴ + (-8x) - 2x³ + [(-2).(-4)]x

= x⁴ + 2x³ - x⁴ -8x - 2x³ + 8x

= (x⁴ - x⁴) + (2x³ - 2x³) + (-8x + 8x)

= 0.

Lời giải bài tập Toán 7 Bài 27: Phép nhân đa thức một biến hay, chi tiết khác:

HĐ3 trang 37 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 27: Phép nhân đa thức một biến

HĐ3 trang 37 Toán 7 Tập 2:

Tính (2x - 3) . (x² - 5x + 1) bằng cách thực hiện các bước sau:

Bước 1. Nhân 2x với đa thức x² - 5x + 1.

Bước 2. Nhân -3 với đa thức x² - 5x + 1.

Bước 3. Cộng các đa thức thu được ở hai bước trên và thu gọn.

Kết quả thu được là tích của đa thức 2x - 3 với đa thức x² - 5x + 1.

Lời giải:

Nhân 2x với đa thức x² - 5x + 1 ta được:

2x . (x² - 5x + 1) = 2x.x² + 2x.(-5x) + 2x.1 = 2x³ -10x² + 2x.

Nhân -3 với đa thức x² - 5x + 1 ta được:

-3(x² - 5x + 1) = -3.x² + (-3).(-5x) + (-3.1) = -3x² + 15x + (-3) = -3x² + 15x - 3.

Cộng các đa thức trên ta được:

(2x³ -10x² + 2x) + (-3x² + 15x - 3)

= 2x³ -10x² + 2x - 3x² + 15x - 3

= 2x³ + (-10x² - 3x²) + (2x + 15x) - 3

= 2x³ + (-13x²) + 17x - 3

= 2x³ - 13x² + 17x - 3

Vậy (2x - 3) . (x² - 5x + 1) = 2x³ - 13x² + 17x - 3.

Lời giải bài tập Toán 7 Bài 27: Phép nhân đa thức một biến hay, chi tiết khác:

Luyện tập 2 trang 38 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 27: Phép nhân đa thức một biến

Luyện tập 2 trang 38 Toán 7 Tập 2: Tính (x³ - 2x² + x -1)(3x - 2). Trình bày lời giải theo hai cách

Lời giải:

Cách 1. Bỏ dấu ngoặc ta được:

(x³ - 2x² + x -1)(3x - 2)

= x³(3x - 2) + (-2x²).(3x - 2) + x.(3x - 2) + (-1)(3x - 2)

= x³.3x + x³.(-2) + (-2x²).3x + (-2x²).(-2) + x.3x + x.(-2) + (-1).3x + (-1).(-2)

= 3x⁴ + (-2x³) + (-6x³) + 4x² + 3x² + (-2x) + (-3x) + 2

= 3x⁴ + (-8x³) + 7x² + (-5x) + 2

= 3x⁴ - 8x³ + 7x² - 5x + 2

Vậy (x³ - 2x² + x -1)(3x - 2) = 3x⁴ - 8x³ + 7x² - 5x + 2.

Cách 2. Đặt phép tính ta được:

Vậy (x³ - 2x² + x -1)(3x - 2) = 3x⁴ - 8x³ + 7x² - 5x + 2.

Lời giải bài tập Toán 7 Bài 27: Phép nhân đa thức một biến hay, chi tiết khác:

Vận dụng 2 trang 38 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 27: Phép nhân đa thức một biến

Vận dụng 2 trang 38 Toán 7 Tập 2: Rút gọn biểu thức (x - 2)(2x³ - x² + 1) + (x - 2)x²(1 - 2x).

Lời giải:

Xét (x - 2)(2x³ - x² + 1) = x(2x³ - x² + 1) + (-2).(2x³ - x² + 1)

= x.2x³ + x.(-x²) + x.1 + (-2).2x³ + (-2).(-x²) + (-2).1

= 2x⁴ + (-x³) + x + (-4x³) + 2x² + (-2)

= 2x⁴ - x³ + x - 4x³ + 2x² - 2

= 2x⁴ + (-x³ - 4x³) + 2x² + x - 2

= 2x⁴ + (-5x³) + 2x² + x - 2

= 2x⁴ - 5x³ + 2x² + x - 2

Xét (x - 2)x²(1 - 2x) = (x - 2)[x².1 + x²(-2x)]

= (x - 2)[x² + (-2x³)]

= x[x² + (-2x³)] + (-2).[x² + (-2x³)]

= x.x² + x.(-2x³) + (-2)x² + (-2).(-2x³)

= x³ + (-2x⁴) - 2x² + 4x³

= x³ - 2x⁴ - 2x² + 4x³

= -2x⁴ + (x³ + 4x³) - 2x²

= -2x⁴ + 5x³ - 2x²

Do đó (x - 2)(2x³ - x² + 1) + (x - 2)x²(1 - 2x)

= (2x⁴ - 5x³ + 2x² + x - 2) + (-2x⁴ + 5x³ - 2x²)

= 2x⁴ - 5x³ + 2x² + x - 2 -2x⁴ + 5x³ - 2x²

= (2x⁴ - 2x⁴) + (- 5x³ + 5x³) + (2x² - 2x²) + x - 2

= x - 2.

Vậy (x - 2)(2x³ - x² + 1) + (x - 2)x²(1 - 2x) = x - 2.

Lời giải bài tập Toán 7 Bài 27: Phép nhân đa thức một biến hay, chi tiết khác:

Vận dụng 3 trang 38 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 27: Phép nhân đa thức một biến

Vận dụng 3 trang 38 Toán 7 Tập 2: Trở lại bài toán đoán tuổi, để giải thích bí mật trong bài toán đoán tuổi của anh Pi, em hãy thực hiện các yêu cầu sau:

- Gọi x là tuổi cần đoán. Tìm hai đa thức (biến x) biểu thị kết quả thứ nhất và kết quả thứ hai.

- Tìm đa thức biểu thị kết quả cuối cùng.

Từ đó hãy nêu cách tìm x.

Lời giải:

Gọi tuổi cần đoán là x tuổi (x $\in \mathbb{N}*$).

Lấy tuổi cộng 1 rồi bình phương lên ta được (x + 1)².

Ta có (x + 1)² = (x + 1).(x + 1) = x.(x + 1) + 1.(x + 1)

= x.x + x.1 + 1.x + 1.1

= x¹⁺¹ + x + x + 1

= x² + 2x + 1

Lấy tuổi trừ 1 rồi bình phương lên ta được (x - 1)².

Ta có (x - 1)² = (x - 1).(x - 1) = x.(x - 1) - 1.(x - 1)

= x[x + (-1)] - (x - 1)

= x.x + x.(-1) - x + 1

= x¹⁺¹ + (-x) - x + 1

= x² - x - x + 1

= x² - 2x + 1

Lấy kết quả thứ nhất trừ đi kết quả thứ hai ta được:

(x² + 2x + 1) - (x² - 2x + 1)

= x² + 2x + 1 - x² + 2x - 1

= (x² - x²) + (2x + 2x) + (1 - 1)

= 4x

Khi đó kết quả cuối cùng là 4x.

Để tìm ra số tuổi cần đoán, ta lấy kết quả cuối cùng chia 4.

Lời giải bài tập Toán 7 Bài 27: Phép nhân đa thức một biến hay, chi tiết khác:

Bài 7.23 trang 38 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 27: Phép nhân đa thức một biến

Bài 7.23 trang 38 Toán 7 Tập 2: Thực hiện các phép nhân sau:

a) 6x² . (2x³ - 3x² + 5x - 4);

b) (-1,2x²) . (2,5x⁴ - 2x³ + x² - 1,5).

Lời giải:

a) 6x² . (2x³ - 3x² + 5x - 4)

= 6x².2x³ + 6x².(-3x²) + 6x².5x + 6x².(-4)

= 6.2.x².x³ + (-18)x².x² + 30x².x + (-24)x²

= 12x⁵ - 18x⁴ + 30x³ - 24x²

b) (-1,2x²) . (2,5x⁴ - 2x³ + x² - 1,5)

= (-1,2x²) . 2,5x⁴ + (-1,2x²) . (-2x³) + (-1,2x²).x² + (-1,2x²).(-1,5)

= (-1,2 . 2,5).x².x⁴ + [(-1,2) . (-2)](x².x³) -1,2x².x² + [(-1,2).(-1,5)]x²

= -3x⁶ + 2,4x⁵ - 1,2x⁴ + 1,8x²

Lời giải bài tập Toán 7 Bài 27: Phép nhân đa thức một biến hay, chi tiết khác:

Bài 7.24 trang 38 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 27: Phép nhân đa thức một biến

Bài 7.24 trang 38 Toán 7 Tập 2: Rút gọn các biểu thức sau:

a) 4x²(5x² + 3) - 6x(3x³ - 2x + 1) - 5x³(2x - 1);

b) $\frac{3}{2}x(x^2-\frac{2}{3}x+2)-\frac{5}{3}{x}^2(x+\frac{6}{5})$.

Lời giải:

a) 4x²(5x² + 3) – 6x(3x³ – 2x + 1) – 5x³(2x – 1)

= 4x².5x² + 4x².3 + (−6x).3x³ + (−6x)(−2x) + (−6x).1 + (−5x³).2x + (−5x³).(−1)

= 20x⁴ + 12x² – 18x⁴ + 12x² – 6x – 10x⁴ + 5x³

= (20x⁴ – 18x⁴ – 10x⁴) + 5x³ + (12x² + 12x²) – 6x

= −8x⁴ + 5x³ + 24x² – 6x

b) $\frac{3}{2}x(x^2-\frac{2}{3}x+2)-\frac{5}{3}{x}^2(x+\frac{6}{5})$

= $\frac{3}{2}$x.x² + $[\frac{3}{2}.\left(\frac{-2}{3}\right)]$x.x + $\frac{3}{2}$x.2 + $(\frac{-5}{3}{x}^2)$.x + $(\frac{-5}{3}{x}^2).\frac{6}{5}$

= $\frac{3}{2}$x³ + (-x²) + 3x + $(-\frac{5}{3}{x}^3)$+ (-2x²)

= $\frac{3}{2}$x³ - x² + 3x $-\frac{5}{3}$x³ - 2x²

= $(\frac{3}{2}{x}^3-\frac{5}{3}{x}^3)$+ (-x² - 2x²) + 3x

= $(\frac{9}{6}{x}^3-\frac{10}{6}{x}^3)$+ (-3x²) + 3x

= $\frac{-1}{6}$x³ - 3x² + 3x

Lời giải bài tập Toán 7 Bài 27: Phép nhân đa thức một biến hay, chi tiết khác:

Bài 7.25 trang 38 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 27: Phép nhân đa thức một biến

Bài 7.25 trang 38 Toán 7 Tập 2: Thực hiện các phép nhân sau:

a) (x² - x) . (2x² - x - 10);

b) (0,2x² - 3x) . 5(x² - 7x + 3).

Lời giải:

a) (x² - x) . (2x² - x - 10)

= x²(2x² - x - 10) + (-x) (2x² - x - 10)

= x².2x² + x².(-x) + x².(-10) + (-x).2x² + (-x).(-x) + (-x).(-10)

= 2x⁴ + (-x³) - 10x² - 2x³ + x² + 10x

= 2x⁴ - x³- 10x² - 2x³ + x² + 10x

= 2x⁴ + (-x³ - 2x³) + (-10x² + x²) + 10x

= 2x⁴ + (-3x³) + (-9x²) + 10x

= 2x⁴ - 3x³ - 9x² + 10x

b) (0,2x² - 3x) . 5(x² - 7x + 3)

= 5. (0,2x² - 3x) . (x² - 7x + 3)

= 5.[0,2x². (x² - 7x + 3) + (-3x) . (x² - 7x + 3)]

= 5. [0,2x².x² + 0,2x².(-7x) + 0,2x².3 + (-3x).x² + (-3x).(-7x) + (-3x).3]

= 5. [0,2x⁴ + (-1,4)x³ + 0,6x² + (-3x³) + 21x² + (-9x)]

= 5. (0,2x⁴ - 1,4x³ + 0,6x² - 3x³ + 21x² - 9x)

= 5. [0,2x⁴ + (- 1,4x³ - 3x³) + (0,6x² + 21x²) - 9x]

= 5. [0,2x⁴ + (-4,4x³) + 21,6x² - 9x]

= 5. (0,2x⁴ - 4,4x³ + 21,6x² - 9x)

= 5.0,2x⁴ + 5. (-4,4x³) + 5. 21,6x² + 5. (-9x)

= x⁴ + (-22x³) + 108x² + (-45x)

= x⁴ - 22x³ + 108x² - 45x

Lời giải bài tập Toán 7 Bài 27: Phép nhân đa thức một biến hay, chi tiết khác:

Bài 7.26 trang 38 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 27: Phép nhân đa thức một biến

Bài 7.26 trang 38 Toán 7 Tập 2:

a) Tính (x² - 2x + 5) . (x - 2).

b) Từ đó hãy suy ra kết quả của phép nhân (x² - 2x + 5) . (2 - x). Giải thích cách làm.

Lời giải:

a) (x² - 2x + 5) . (x - 2)

= x²(x - 2) + (-2x).(x - 2) + 5.(x - 2)

= x².x + x².(-2) + (-2x).x + (-2x).(-2) + 5x + 5.(-2)

= x³ - 2x² - 2x² + 4x + 5x -10

= x³ - 4x² + 9x - 10

Vậy (x² - 2x + 5) . (x - 2) = x³ - 4x² + 9x - 10.

b) (x² - 2x + 5) . (2 - x) = -x³ + 4x² - 9x + 10.

Ta thấy 2 - x = -x + 2 = - (x - 2).

Do đó (x² - 2x + 5) . (2 - x) = (x² - 2x + 5). -(x - 2) = - (x² - 2x + 5) . (x - 2).

Vậy (x² - 2x + 5) . (2 - x) = -(x³ - 4x² + 9x - 10) = -x³ + 4x² - 9x + 10.

Lời giải bài tập Toán 7 Bài 27: Phép nhân đa thức một biến hay, chi tiết khác:

Bài 7.27 trang 38 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 27: Phép nhân đa thức một biến

Bài 7.27 trang 38 Toán 7 Tập 2: Giả sử ba kích thước của một hình hộp chữ nhật là x; x + 1; x - 1 (cm) với x > 1. Tìm đa thức biểu thị thể tích (đơn vị: cm3) của hình hộp chữ nhật đó.

Lời giải:

Thể tích của hình hộp chữ nhật đó là:

x(x + 1)(x - 1) = (x.x + x.1)(x - 1)

= (x² + x)(x - 1)

= x²(x - 1) + x(x - 1)

= x².x + x².(-1) + x.x + x.(-1)

= x³ - x² + x² - x

= x³ - x

Vậy đa thức biểu thị thể tích (đơn vị: cm³) của hình hộp chữ nhật đó là x³ - x.

Lời giải bài tập Toán 7 Bài 27: Phép nhân đa thức một biến hay, chi tiết khác:

Bài 7.28 trang 38 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 27: Phép nhân đa thức một biến

Bài 7.28 trang 38 Toán 7 Tập 2: Thực hiện các phép nhân hai đa thức sau:

a) 5x³ - 2x² + 4x - 4 và x³ + 3x² - 5;

b) -2,5x⁴ + 0,5x² + 1 và 4x³ - 2x + 6.

Lời giải:

a) (5x³ - 2x² + 4x - 4). (x³ + 3x² - 5)

= 5x³. (x³ + 3x² - 5) + (-2x²). (x³ + 3x² - 5) + 4x. (x³ + 3x² - 5) + (-4). (x³ + 3x² - 5)

= 5x³.x³ + 5x³.3x² + 5x³. (-5) + (-2x²).x³ + (-2x²).3x² + (-2x²).(-5)

+ 4x.x³ + 4x.3x² + 4x. (-5) + (-4)x³ + (-4).3x² + (-4).(-5)

= 5x⁶ + 15x⁵ - 25x³ - 2x⁵ - 6x⁴ + 10x² + 4x⁴ + 12x³ - 20x - 4x³ - 12x² + 20

= 5x⁶ + (15x⁵ - 2x⁵) + (-6x⁴ + 4x⁴) + (-25x³ + 12x³ - 4x³) + (10x² - 12x²) - 20x + 20

= 5x⁶ + 13x⁵ + (-2x⁴) + (-17x³) + (-2x²) - 20x + 20

= 5x⁶ + 13x⁵ - 2x⁴ - 17x³ - 2x² - 20x + 20

b) (-2,5x⁴ + 0,5x² + 1). (4x³ - 2x + 6)

= (-2,5x⁴).(4x³ - 2x + 6) + 0,5x².(4x³ - 2x + 6) + 1.(4x³ - 2x + 6)

= (-2,5x⁴). 4x³ + (-2,5x⁴). (-2x) + (-2,5x⁴). 6 + 0,5x². 4x³ + 0,5x². (-2x) + 0,5x². 6

+ 1. 4x³ + 1. (-2x) + 1. 6

= -10x⁷ + 5x⁵ + (-15x⁴) + 2x⁵ + (-x³) + 3x² + 4x³ + (-2x) + 6

= -10x⁷ + 5x⁵ - 15x⁴ + 2x⁵ - x³ + 3x² + 4x³ - 2x + 6

= -10x⁷ + (5x⁵ + 2x⁵) - 15x⁴ + (-x³ + 4x³) + 3x² - 2x + 6

= -10x⁷ + 7x⁵ - 15x⁴ + 3x³ + 3x² - 2x + 6

Lời giải bài tập Toán 7 Bài 27: Phép nhân đa thức một biến hay, chi tiết khác:

Bài 7.29 trang 38 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 27: Phép nhân đa thức một biến

Bài 7.29 trang 38 Toán 7 Tập 2: Người ta dùng những chiếc cọc để rào một mảnh vườn hình chữ nhật sao cho mỗi góc vườn đều có một chiếc cọc và hai cọc liên tiếp cắm cách nhau 0,1 m. Biết rằng số cọc dùng để rào hết chiều dài của vườn nhiều hơn số cọc dùng để rào hết chiều rộng là 20 chiếc. Gọi số cọc dùng để rào hết chiều rộng là x. Tìm đa thức biểu thị diện tích của mảnh vườn đó.

Lời giải:

Số cọc dùng để rào hết chiều dài của mảnh vườn là x + 20 cọc.

Khoảng cách giữa hai cọc liên tiếp là 0,1 m.

Giữa x cọc sẽ có x - 1 khoảng cách.

Do đó độ dài của chiều rộng mảnh vườn là: 0,1. (x - 1) m.

Giữa x + 20 cọc sẽ có x + 19 khoảng cách.

Do đó độ dài của chiều dài mảnh vườn là: 0,1. (x + 19) m.

Khi đó diện tích của mảnh vườn là:

0,1. (x - 1). 0,1. (x + 19) = 0,1. 0,1. (x - 1). (x + 19)

= 0,01. [x.x + x.19 + (-1).x + (-1).19]

= 0,01. (x² + 19x - x - 19)

= 0,01. (x² + 18x - 19)

= 0,01.x² + 0,01. 18x + 0,01. (-19)

= 0,01x² + 0,18x - 0,19

Vậy đa thức biểu thị diện tích của mảnh vườn là 0,01x² + 0,18x - 0,19.

Lời giải bài tập Toán 7 Bài 27: Phép nhân đa thức một biến hay, chi tiết khác:

Sách bài tập Toán 7 Bài 27: Phép nhân đa thức một biến - Kết nối tri thức

Với giải sách bài tập Toán 7 Bài 27: Phép nhân đa thức một biến sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Bài 27.

Giải SBT Toán 7 Bài 27: Phép nhân đa thức một biến - Kết nối tri thức

Giải SBT Toán 7 trang 30 Tập 2

Vở thực hành Toán 7 Bài 27: Phép nhân đa thức một biến - Kết nối tri thức

Với giải vở thực hành Toán lớp 7 Bài 27: Phép nhân đa thức một biến sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập về nhà trong VTH Toán 7 Bài 27.

Giải vở thực hành Toán 7 Bài 27: Phép nhân đa thức một biến - Kết nối tri thức

Giải VTH Toán 7 trang 40 Tập 2

Phép nhân đa thức một biến (Lý thuyết Toán lớp 7) - Kết nối tri thức

Với tóm tắt lý thuyết Toán 7 Bài 27: Phép nhân đa thức một biến sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Phép nhân đa thức một biến (Lý thuyết Toán lớp 7) - Kết nối tri thức

Lý thuyết Phép nhân đa thức một biến

1. Nhân đơn thức với đa thức

Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức vời từng hạng tử của đa thức rồi cộng các tích với nhau.

Ví dụ:

Muốn tính $\left(-3x^2\right)\cdot \left(x^3-\frac{1}{3}x+4\right)$ ta làm như sau:

$\left(-3x^2\right)\cdot \left(x^3-\frac{1}{3}x+4\right)$ = $\left(-3x^2\right)\cdot \left(x^3\right)+\left(-3x^2\right)\cdot \left(-\frac{1}{3}x\right)+\left(-3x^2\right)\cdot 4$

= – 3x⁵ + x³ – 12x².

2. Nhân đa thức với đa thức

Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.

Ví dụ:

Muốn tính (x + 2).(3x² – 4x + 5) ta làm như sau:

(x + 2).(3x² – 4x + 5) = x.(3x² – 4x + 5) + 2.(3x² – 4x + 5)

= x.3x² + x.( – 4x) + x.5 + 2.3x² +2.( – 4x) + 2.5

= 3x³ – 4x² + 5x + 6x² – 8x + 10

= 3x³ + (– 4x² + 6x²) + (5x – 8x) + 10

= 3x³ + 2x² – 3x + 10.

Chú ý:

• Ta có thể trình bày phép nhân một đa thức với một đa thức bằng cách đặt tính.

Khi trình bày theo cách này ta cần:

+ Nhân lần lượt mỗi hạng tử ở dòng dưới với đa thức ở dòng trên và viết kết quả trong một dòng riêng.

+ Viết các dòng sao cho các hạng tử cùng bậc thẳng cột với nhau (để thực hiện phép cộng theo cột).

+ Khi nhân các hạng tử ở dòng dưới với đa thức ở dòng trên, ta nên nhân các hạng tử theo thứ tự từ bậc thấp đến bậc cao.

Chẳng hạn: Đặt tính nhân (x + 3).(2x² – 3x – 5), ta làm như sau:

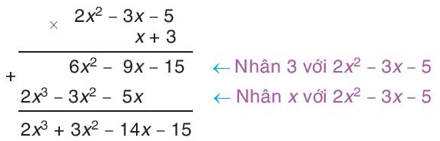
• Phép nhân đa thức cũng có các tính chất:

+ Giao hoán: A.B = B.A.

+ Kết hợp: (A.B).C = A.(B.C).

+ Phân phối đối với phép cộng: A.(B + C) = A.B + A.C.

Bài tập Phép nhân đa thức một biến

Bài 1. Thực hiện các phép nhân sau:

a) 5x².(2x³ – 4x² + 3x – 1);

b) (– 1,2x²).(5x⁴ – 2x³ + 3x² – 2,5).

Hướng dẫn giải

a) 5x².(2x³ – 4x² + 3x – 1)

= 5x².2x³ + 5x².( – 4x²) + 5x².3x + 5x².( – 1)

= 10x⁵ – 20x⁴ + 15x³ – 5x²

b) (– 1,2x²).(5x⁴ – 2x³ + 3x² – 2,5)

= (– 1,2x²).5x⁴ + (– 1,2x²).( – 2x³) + (– 1,2x²).( 3x²) + (– 1,2x²).( – 2,5)

= – 6x⁶ + 2,4x⁵ – 3,6x⁴ + 3x²

Bài 2. Thực hiện các phép nhân sau:

a) (x² – 3x).(x² – 2x – 8);

b) (0,2x² + x).(x² – 3x + 7).

Hướng dẫn giải

a) (x² – 3x).(x² – 2x – 8)

= x². (x² – 2x – 8) – 3x. (x² – 2x – 8)

= x².x² + x².(– 2x) + x².(– 8) – 3x.x² – 3x.(– 2x) – 3x.( – 8)

= x⁴ – 2x³ – 8x² – 3x³ + 6x² + 24x

= x⁴ – (2x³ + 3x³) + (– 8x² + 6x²) + 24x

= x⁴ – 5x³ – 2x² + 24x.

b) (0,2x² + x).(x² – 3x + 7)

= 0,2x². (x² – 3x + 7) + x. (x² – 3x + 7)

= 0,2x².x² + 0,2x².( – 3x) + 0,2x².7 + x.x² + x.( – 3x) + x.7

= 0,2x⁴ – 0,6x³ + 1,4x² + x³ – 3x² + 7x

= 0,2x⁴ + (– 0,6x³ + x³) + (1,4x² – 3x²) + 7x

= 0,2x⁴ + 0,4x³ – 1,6x² + 7x.

Bài 3. Tìm x, biết rằng:

a) (x – 7)(2x³ – x² + 1) + (x – 7)x²(1 – 2x) = 2;

b) (2x + 1)(2x – 3) – (4x + 1)(x + 2) = 8.

Hướng dẫn giải

a) (x – 7)(2x³ – x² + 1) + (x – 7)x²(1 – 2x) = 2

(x – 7)[(2x³ – x² + 1) + x²(1 – 2x)] = 2

(x – 7)[2x³ – x² + 1 + x² – 2x³] = 2

(x – 7)[(2x³ – 2x³) + (– x² + x²) + 1] = 2

(x – 7).1 = 2

x – 7 = 2

x = 2 + 7

x = 9

Vậy x = 9.

b) (2x + 1)(2x – 3) – (4x + 1)(x + 2) = 8

2x(2x – 3) + 1.(2x – 3) – [4x(x + 2) + 1.(x + 2)] = 8

4x² – 6x + 2x – 3 – [4x² + 8x + x + 2] = 8

4x² – 6x + 2x – 3 – 4x² – 8x – x – 2 = 8

(4x² – 4x²) + (– 6x + 2x – 8x – x) – (3 + 2) = 8

– 13x – 5 = 8

– 13x = 8 + 5

– 13x = 13

x = 13 : (– 13)

x = – 1

Vậy x = – 1.

Học tốt Phép nhân đa thức một biến

Các bài học để học tốt Phép nhân đa thức một biến Toán lớp 7 hay khác:

15 Bài tập Phép nhân đa thức một biến (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 7

Với 15 bài tập trắc nghiệm Phép nhân đa thức một biến Toán lớp 7 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 7.

15 Bài tập Phép nhân đa thức một biến (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 7

Xem thử

Chỉ 150k mua trọn bộ trắc nghiệm Toán 7 Kết nối tri thức (cả năm) có lời giải chi tiết, bản word trình bày đẹp mắt, dễ dàng chỉnh sửa: