Với giải bài tập Toán 8 Bài 7: Hình vuông sách Cánh diều hay nhất, chi tiết giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 Bài 7.

Giải Toán 8 Cánh diều Bài 7: Hình vuông

Video Giải Toán 8 Bài 7: Hình vuông - Cô Vũ Chuyên (Giáo viên VietJack)

Giải Toán 8 trang 116

Khởi động trang 116 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài 7: Hình vuông - Cánh diều

Khởi động trang 116 Toán 8 Tập 1: Một số hoạ tiết và hoa văn trên thổ cẩm (Hình 64) có dạng hình vuông.

Hình vuông có những tính chất gì? Có những dấu hiệu nào để nhận biết một tứ giác là hình vuông?

Lời giải:

‒ Hình vuông có:

+ Bốn góc vuông và bốn cạnh bằng nhau.

+ Các cạnh đối song song;

+ Hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường;

+ Hai đường chéo là các đường phân giác của các góc ở đỉnh.

‒ Dấu hiệu nhận biết hình vuông:

+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

+ Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.

+ Hình thoi có hai đường chéo bằng nhau là hình vuông.

+ Hình thoi có một góc vuông là hình vuông.

Lời giải bài tập Toán 8 Bài 7: Hình vuông hay, chi tiết khác:

Hoạt động 1 trang 116 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài 7: Hình vuông - Cánh diều

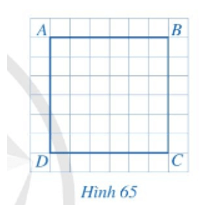
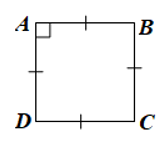
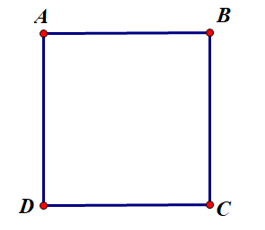
Hoạt động 1 trang 116 Toán 8 Tập 1: Cho biết các góc và các cạnh của tứ giác ABCD ở Hình 65 có đặc điểm gì.

Lời giải:

Tứ giác ABCD ở Hình 65 có AB = BC = CD = DA và $\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90°$.

Lời giải bài tập Toán 8 Bài 7: Hình vuông hay, chi tiết khác:

Hoạt động 2 trang 117 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài 7: Hình vuông - Cánh diều

Hoạt động 2 trang 117 Toán 8 Tập 1: a) Mỗi hình vuông có là một hình chữ nhật hay không?

b) Mỗi hình vuông có là một hình thoi hay không?

Lời giải:

a) Mỗi hình vuông là một hình chữ nhật (do nó có 4 góc vuông).

b) Mỗi hình vuông là một hình thoi (do nó có 4 cạnh bằng nhau).

Lời giải bài tập Toán 8 Bài 7: Hình vuông hay, chi tiết khác:

Luyện tập 1 trang 117 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài 7: Hình vuông - Cánh diều

Luyện tập 1 trang 117 Toán 8 Tập 1: Cho hình vuông ABCD. Tính số đo các góc CAB, DAC.

Lời giải:

Do ABCD là hình vuông nên $\widehat{DAB}=90°$ và AC là tia phân giác của $\widehat{DAB}$.

Do đó $\widehat{CAB}=\widehat{DAC}=\frac{1}{2}\widehat{DAB}=\frac{1}{2}.90°=45°$.

Lời giải bài tập Toán 8 Bài 7: Hình vuông hay, chi tiết khác:

Hoạt động 3 trang 118 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài 7: Hình vuông - Cánh diều

Hoạt động 3 trang 118 Toán 8 Tập 1: a) Cho hình chữ nhật ABCD có hai cạnh kề AB và BC bằng nhau. ABCD có phải là hình vuông hay không?

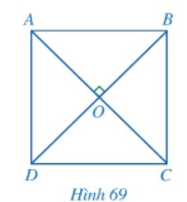
b) Cho hình chữ nhật ABCD có hai đường chéo AC và BD vuông góc với nhau (Hình 69).

• Đường thẳng AC có phải là đường trung trực của thẳng BD hay không? đoạn

• ABCD có phải là hình vuông hay không?

c) Cho hình chữ nhật ABCD có AC là tia phân giác của góc DAB.

• Tam giác ABC có phải là tam giác vuông cân hay không?

• ABCD có phải là hình vuông hay không?

Lời giải:

a) Do ABCD là hình chữ nhật nên $\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90°$ và AB = CD, AD = BC.

Mà AB = BC nên AB = BC = CD = DA.

Tứ giác ABCD có 4 góc vuông và 4 cạnh bằng nhau nên là hình vuông.

b) • Do ABCD là hình chữ nhật nên hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường.

Mà AC ⊥ BD

Do đó AC là đường trung trực của đoạn thẳng BD.

• Do ABCD là hình chữ nhật nên $\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90°$ và AB = CD; AD = BC.

Do AC là đường trung trực của đoạn thẳng BD nên AB = AD và CB = CD.

Do đó AB = BC = CD = DA.

Tứ giác ABCD có 4 góc vuông và 4 cạnh bằng nhau nên là hình vuông.

c)

• Do ABCD là hình chữ nhật nên $\widehat{B}=90°$ và AD // BC

Từ AD // BC suy ra $\widehat{DAC}=\widehat{BCA}$ (so le trong).

Mặt khác, AC là tia phân giác của góc DAB nên $\widehat{DAC}=\widehat{BAC}$

Suy ra $\widehat{BAC}=\widehat{BCA}$ (vì cùng bằng $\widehat{DAC}$).

Tam giác ABC vuông tại B ($\widehat{B}=90°$) có $\widehat{BAC}=\widehat{BCA}$

Do đó ΔABC vuông cân tại B.

• Do ΔABC vuông cân tại B nên BA = BC.

Theo kết quả câu a, hình chữ nhật ABCD có hai cạnh kề BA và BC bằng nhau nên là hình vuông.

Lời giải bài tập Toán 8 Bài 7: Hình vuông hay, chi tiết khác:

Luyện tập 2 trang 118 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài 7: Hình vuông - Cánh diều

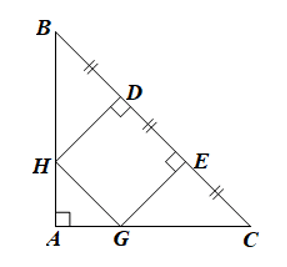
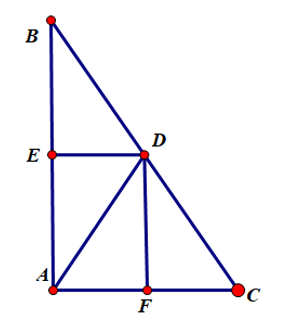
Luyện tập 2 trang 118 Toán 8 Tập 1: Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy các điểm D, E sao cho BD = DE = EC.

Qua D và E kẻ đường thẳng vuông góc với BC, chúng cắt AB và AC lần lượt tại H và G. Chứng minh tứ giác DEGH là hình vuông.

Lời giải:

• Do tam giác ABC là tam giác vuông cân tại A nên $\widehat{ABC}=\widehat{ACB}=45°$.

Xét ΔBDH vuông tại D có $\widehat{DBH}+\widehat{DHB}=90°$ 

Suy ra $\widehat{DHB}=90°-\widehat{DBH}=90°-45°=45°$.

Khi đó ΔBDH vuông cân tại D, nên DB = DH.

Chứng minh tương tự với ΔGEC ta cũng có ΔGEC vuông cân tại E nên EG = EC.

Theo bài, BD = DE = EC.

Do đó DH = DE = EG.

• Xét tứ giác DEGH có DH // GE (cùng vuông góc với BC) và DH = DE

Do đó tứ giác DEGH là hình bình hành.

Lại có $\widehat{HDE}=90$ nên DEGH là hình chữ nhật

Mặt khác DEGH có hai cạnh kề DH và DE bằng nhau nên là hình vuông.

Lời giải bài tập Toán 8 Bài 7: Hình vuông hay, chi tiết khác:

Bài 1 trang 119 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài 7: Hình vuông - Cánh diều

Bài 1 trang 119 Toán 8 Tập 1: Cho hình thoi ABCD có AC = BD. Chứng minh ABCD là hình vuông.

Lời giải:

Do ABCD là hình thoi nên cũng là hình bình hành.

Hình bình hành có hai đường chéo AC và BD bằng nhau nên là hình chữ nhật.

Mà AD = AB (do ABCD là hình thoi)

Hình chữ nhật ABCD có hai cạnh kề bằng nhau (AD = AB) nên là hình vuông.

Lời giải bài tập Toán 8 Bài 7: Hình vuông hay, chi tiết khác:

Bài 2 trang 119 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài 7: Hình vuông - Cánh diều

Bài 2 trang 119 Toán 8 Tập 1: Cho hình thoi ABCD có $\widehat{A}=90°$. Chứng minh ABCD là hình vuông.

Lời giải:

Do ABCD là hình thoi nên cũng là hình bình hành.

Lại có $\widehat{A}=90°$ nên hình bình hành ABCD là hình chữ nhật.

Mà AD = AB (do ABCD là hình thoi)

Hình chữ nhật ABCD có hai cạnh kề bằng nhau (AD = AB) nên là hình vuông.

Lời giải bài tập Toán 8 Bài 7: Hình vuông hay, chi tiết khác:

Bài 3 trang 119 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài 7: Hình vuông - Cánh diều

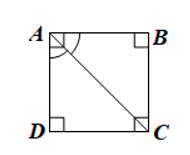
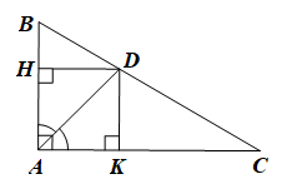
Bài 3 trang 119 Toán 8 Tập 1: Cho tam giác ABC vuông tại A có đường phân giác AD. Gọi H, K lần lượt là hình chiếu của D trên AB, AC. Chứng minh tứ giác AHDK là hình vuông.

Lời giải:

Do H, K lần lượt là hình chiếu của D trên AB, AC nên DH ⊥ AB và DK ⊥ AC

Hay $\widehat{H}=\widehat{K}=90°$.

Tứ giác AHDK có $\widehat{A}=\widehat{H}=\widehat{K}=90°$ nên AHDK là hình chữ nhật.

Mà AD là tia phân giác của góc HAK nên AHDK là hình vuông.

Lời giải bài tập Toán 8 Bài 7: Hình vuông hay, chi tiết khác:

Bài 4 trang 119 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài 7: Hình vuông - Cánh diều

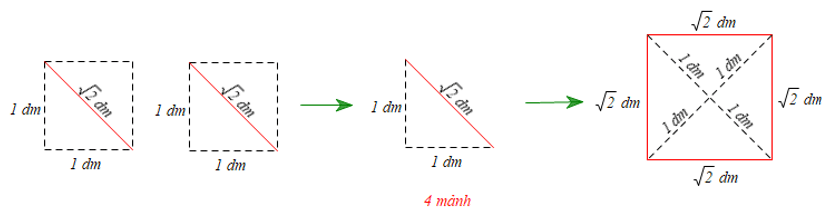
Bài 4 trang 119 Toán 8 Tập 1: Cho hai mảnh giấy, mỗi mảnh có dạng hình vuông với độ dài cạnh là 1 dm. Hãy trình bày cách cắt ghép hai mảnh giấy đó để được một hình vuông có độ dài cạnh là $\sqrt{2}$ dm.

Lời giải:

‒ Gấp và cắt hai mảnh giấy hình vuông thành 4 mảnh tam giác vuông (hình vẽ).

‒ Ghép 4 mảnh tam giác vuông, với cạnh huyền tam giác là cạnh của hình vuông mới (hình vẽ).

Lời giải bài tập Toán 8 Bài 7: Hình vuông hay, chi tiết khác:

Bài 5 trang 119 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài 7: Hình vuông - Cánh diều

Bài 5 trang 119 Toán 8 Tập 1: Bạn Thảo có một mảnh giấy có dạng hình tròn. Bạn Thảo đố bạn Minh: Không dùng thước thẳng và compa, làm thế nào có thể xác định tâm của hình tròn và chọn ra 4 vị trí trên đường tròn đó để chúng là 4 đỉnh của một hình vuông?

Bạn Minh đã làm như sau:

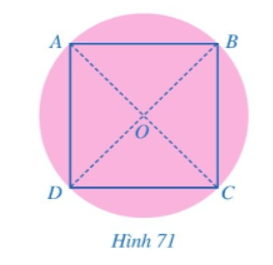
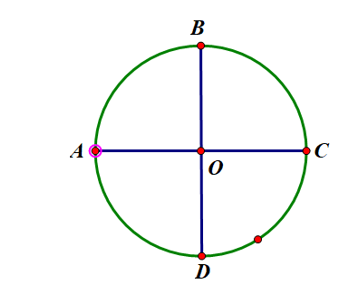
Bước 1. Gấp mảnh giấy sao cho hai nửa hình tròn trùng khít nhau. Nét gấp thẳng tạo thành đường kính của hình tròn. Ta đánh dấu hai đầu mút của đường kính đó là hai điểm A, C.

Bước 2. Tiếp tục gấp mảnh giấy (có dạng nửa hình tròn) ở Bước 1 sao cho hai nửa mới của nửa hình tròn đó lại trùng khít nhau. Trải miếng bìa về dạng hình tròn ban đầu, ta được nét gấp mới là một đường kính khác của hình tròn.

Bước 3. Ta đánh dấu giao điểm của hai đường kính là O và hai đầu mút của đường kính mới là hai điểm B, D. Khi đó O là tâm của hình tròn và tứ giác ABCD là hình vuông (Hình 71).

Em hãy giải thích cách làm của bạn Minh.

Lời giải:

Ở bước 2, do bạn Minh đã gấp mảnh giấy (có dạng nửa hình tròn) sao cho hai nửa mới của nửa hình tròn đó lại trùng khít nhau nên hai đường kính AC và BD vuông góc với nhau tại O và OA = OB = OC = OD.

Do đó AC ⊥ BD tại trung điểm O của mỗi đường

Khi đó tứ giác ABCD là hình thoi

Mặt khác, hai đường chéo AC và BD của hình thoi ABCD bằng nhau (do cùng là đường kính của hình tròn) nên ABCD là hình vuông có tâm là O.

Lời giải bài tập Toán 8 Bài 7: Hình vuông hay, chi tiết khác:

Sách bài tập Toán 8 Cánh diều Bài 7: Hình vuông

Với giải sách bài tập Toán 8 Bài 7: Hình vuông sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 8 Bài 7.

Giải SBT Toán 8 Bài 7: Hình vuông - Cánh diều

Hình vuông (Lý thuyết Toán lớp 8) | Cánh diều

Với tóm tắt lý thuyết Toán lớp 8 Bài 7: Hình vuông sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Hình vuông (Lý thuyết Toán lớp 8) | Cánh diều

Lý thuyết Hình vuông

1. Định nghĩa

Ta có định nghĩa:

Hình vuông là hình tứ giác có bốn góc vuông và bốn cạnh bằng nhau.

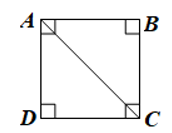
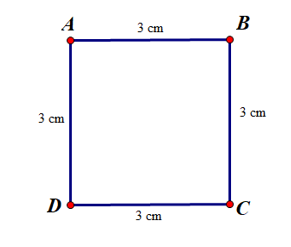
Ví dụ:  Chứng minh tứ giác ABCD là hình vuông.

Hướng dẫn giải

 Ta có $\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90°$  và AB = BC = CD = DA (vì cùng bằng 3 cm).

Suy ra tứ giác ABCD là hình vuông.

2. Tính chất

Ta có định lý sau:

Trong một hình vuông:

- Các cạnh đối song song;

- Hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường;

- Hai đường chéo là các đường phân giác của các góc ở đỉnh.

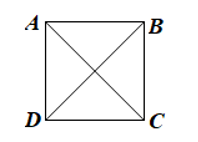
Ví dụ: Cho hình vuông ABCD có hai đường chéo AC và BD cắt nhau tại O. Chứng minh các tam giác OAB, OBC, OCD, ODA là những tam giác vuông cân.

Hướng dẫn giải

Do ABCD là hình vuông cân nên AC = BD,$\text{AC}\perp \text{BD}$ , AC và BD cắt nhau tại trung điểm O của mỗi đường.

Suy ra các tam giác OAB, OBC, OCD, ODA là những tam giác vuông cân tại O và OA= OB = OC = OD.

Vậy các tam giác OAB, OBC, OCD, ODA là những tam giác vuông cân.

3. Dấu hiệu nhận biết

Ta có những dấu hiệu nhận biết:

- Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông;

- Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông;

- Hình chữ nhật có một đường chéo là đường phân giác cảu một góc là hình vuông.

Ví dụ: Cho đường tròn tâm O. Giả sử AC và BD là hai đường kính của đường trong sao cho $\text{AC}\perp \text{BD}$ . Chứng minh ABCD là hình vuông.

Hướng dẫn giải

Vì tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường nên ABCD là hình bình hành.

Hình bình hành ABCD có AC = BD nên ABCD là hình chữ nhật.

Hình chữ nhật ABCD có hai đừng chéo vuông góc với nhau nên ABCD là hình vuông.

Vậy ABCD là hình vuông.

Bài tập Hình vuông

Bài 1. Cho tam giác ABC vuông tại A. Phân giác trong AD của góc A (D ∈ BC ). Vẽ DF ⊥ AC, DE ⊥ AB. Chứng minh tứ giác AEDF là hình vuông.

Hướng dẫn giải

Xét tứ giác AEDF có:

$\widehat{A}=\widehat{E}=\widehat{F}=90°$

Suy ra AEDF là hình chữ nhật (1)

Theo giả thiết ta có: AD là đường phân giác của góc $\widehat{\text{A}}$ .

Suy ra $\widehat{\text{EAD}}=\widehat{\text{DAF}}=45°$ .

Xét ΔAED có: $\widehat{\text{AED}}=90°$

$\widehat{\text{EAD}}=45°$

Suy ra $\widehat{\text{EDA}}=45°$ .

Suy ra ΔAED vuông cân tại E nên AE = ED (2).

Từ (1) và (2) suy ra AEDF là hình vuông.

Vậy AEDF là hình vuông.

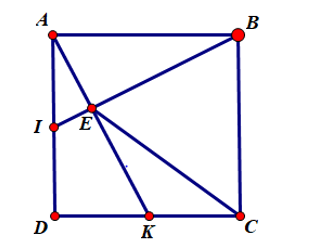
Bài 2. Cho hình vuông ABCD. Gọi I, K lần lượt là trung điểm của AD và DC.

a) Chứng minh rằng BI ⊥ AK.

b) Gọi E là giao điểm của BI và AK. Chứng minh rằng $\widehat{EBC}=\widehat{EKD}$ .

Hướng dẫn giải

Xét ∆BAI và ∆ADK có:

AB = AD

$AI=DK=\frac{1}{2}AB=\frac{1}{2}DA$

$\widehat{A}=\widehat{D}$

Suy ra ∆BAI = ∆ADK  (c.g.c)

Suy ra $\widehat{ABI}=\widehat{DAK}$  (góc tương ứng bằng nhau)

Mà $\widehat{IAE}+\widehat{EAB}=90°$

Suy ra $\widehat{ABI}+\widehat{EAB}=90°$

• Xét ∆ABE có $\widehat{EAB}+\widehat{ABE}+\widehat{AEB}=180°$

Suy ra $\widehat{AEB}=180°-\left(\widehat{ABE}+\widehat{BAE}\right)=180°-90°=90°$

Hay AK ⊥ BI (đpcm)

• Xét tứ giác EBCK có $\widehat{KEB}+\widehat{EBC}+\widehat{BCK}+\widehat{CKE}=360°$

Suy ra $\widehat{EBC}+\widehat{EKC}=180°$

Mà $\widehat{AKD}+\widehat{AKC}=180°$ .

Do đó $\widehat{EBC}=\widehat{EKD}$ .

Học tốt Hình vuông

Các bài học để học tốt Hình vuông Toán lớp 8 hay khác:

15 Bài tập Hình vuông (có đáp án) - Cánh diều Trắc nghiệm Toán 8

Với 15 bài tập trắc nghiệm Hình vuông Toán lớp 8 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Cánh diều sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 8.

15 Bài tập Hình vuông (có đáp án) - Cánh diều Trắc nghiệm Toán 8

Nội dung đang được cập nhật ...

Xem thêm bài tập trắc nghiệm Toán lớp 8 Cánh diều có đáp án hay khác: