Với giải bài tập Toán 8 Bài tập cuối chương 4 trang 88, 89 sách Cánh diều hay nhất, chi tiết giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 Bài tập cuối chương 4.

Giải Toán 8 Cánh diều Bài tập cuối chương 4 (trang 88, 89)

Video Giải Toán 8 Bài tập cuối chương 4 - Cô Vũ Chuyên (Giáo viên VietJack)

Giải Toán 8 trang 88

Bài 1 trang 88 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài tập cuối chương 4 - Cánh diều

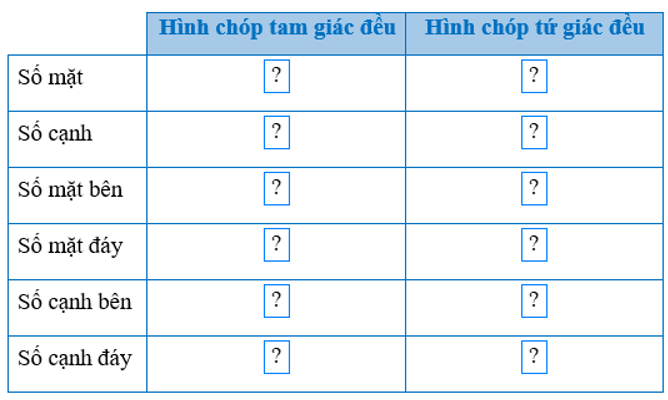
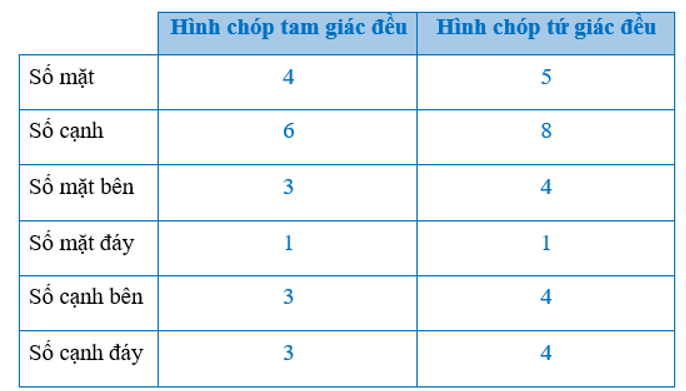
Bài 1 trang 88 Toán 8 Tập 1: Quan sát các Hình 4, Hình 14 và tìm số thích hợp cho  trong bảng sau:

Lời giải:

Lời giải bài tập Toán 8 Bài tập cuối chương 4 hay, chi tiết khác:

Bài 2 trang 88 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài tập cuối chương 4 - Cánh diều

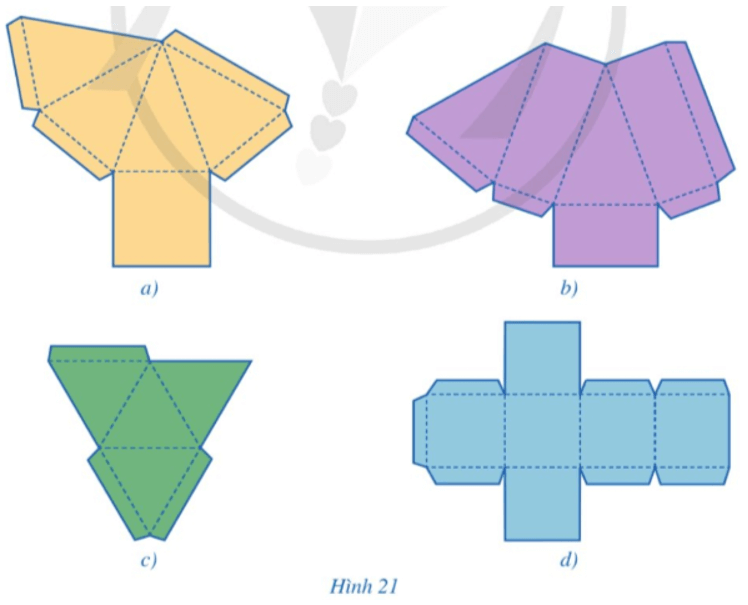
Bài 2 trang 88 Toán 8 Tập 1: Trong các miếng bìa ở hình 21a, 21b, 21c, 21d, miếng bìa nào có thể gấp (theo các nét đứt) và dán lại để được hình chóp tam giác đều? Hình chóp tứ giác đều?

Lời giải:

• Để miếng bìa gấp và dán lại được hình chóp tam giác đều, miếng bìa đó cần có 4 mặt, trong đó có 1 mặt là tam giác đều và 3 mặt bên là các tam giác cân bằng nhau.

Quan sát hình 21 ta thấy chỉ có miếng bìa ở hình 21c thỏa mãn điều kiện 4 mặt đều là tam giác, đặc biệt trong miếng bìa này là 4 hình tam giác đều.

• Để miếng bìa gấp và dán lại được hình chóp tứ giác đều, miếng bìa đó cần có 5 mặt, trong đó có 1 mặt là hình vuông và 4 mặt bên là các tam giác cân bằng nhau.

Quan sát hình 21 ta thấy chỉ có miếng bìa ở hình 21a thỏa mãn điều kiện trên.

Vậy khi gấp (theo các nét đứt) và dán lại các miếng bìa trên, miếng bìa ở hình 21c được hình chóp tam giác đều; miếng bìa ở hình 21a được hình chóp tứ giác đều.

Lời giải bài tập Toán 8 Bài tập cuối chương 4 hay, chi tiết khác:

Bài 3 trang 89 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài tập cuối chương 4 - Cánh diều

Bài 3 trang 89 Toán 8 Tập 1: Cho một hình chóp tam giác đều có độ dài cạnh đáy là 20 cm và độ dài trung đoạn là 30 cm. Tính diện tích xung quanh của hình chóp tam giác đều đó.

Lời giải:

Diện tích xung quanh của hình chóp tam giác đều đó là:

$S_{xq}=\frac{1}{2}.\left(20.3\right).30=900\left(c{m}^2\right)$

Lời giải bài tập Toán 8 Bài tập cuối chương 4 hay, chi tiết khác:

Bài 4 trang 89 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài tập cuối chương 4 - Cánh diều

Bài 4 trang 89 Toán 8 Tập 1: Cho một hình chóp tứ giác đều có độ dài cạnh đáy là 10 cm và độ dài trung đoạn là 13 cm. Tính diện tích xung quanh của hình chóp tứ giác đều đó.

Lời giải:

Diện tích xung quanh của hình chóp tứ giác đều đó là:

$S_{xq}=\frac{1}{2}.\left(10.4\right).13=260\left(c{m}^2\right)$

Lời giải bài tập Toán 8 Bài tập cuối chương 4 hay, chi tiết khác:

Bài 5 trang 89 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài tập cuối chương 4 - Cánh diều

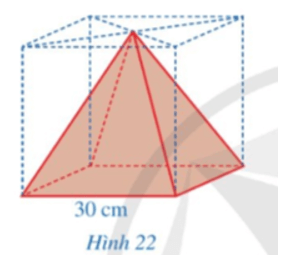
Bài 5 trang 89 Toán 8 Tập 1: Hình 22 mô tả một vật thể có dạng hình chóp tứ giác đều được tạo ra sau khi cắt bỏ một phần từ một khúc gỗ có dạng hình lập phương với cạnh là 30 cm. Tính thể tích của phần gỗ đã bị cắt bỏ.

Lời giải:

Thể tích của hình lập phương có cạnh là 30 cm là:

V₁ = 30³ = 27 000 (cm³).

Thể tích của vật thể có dạng hình chóp tứ giác đều là:

$V_2=\frac{1}{3}{.30}^2.30=9000\left(c{m}^3\right)$.

Thể tích của phần khúc gỗ đã bị cắt bỏ là:

V = V₁ – V₂ = 27 000 – 9 000 = 18 000 (cm³).

Lời giải bài tập Toán 8 Bài tập cuối chương 4 hay, chi tiết khác:

Bài 6 trang 89 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài tập cuối chương 4 - Cánh diều

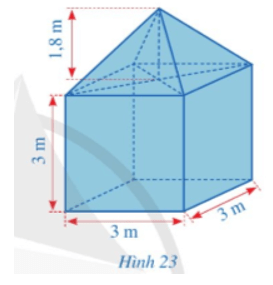
Bài 6 trang 89 Toán 8 Tập 1: Hình 23 mô tả một lều trại gồm hai phần: phần dưới có dạng hình lập phương với cạnh là 3 m; phần trên có dạng hình chóp tứ giác đều với chiều cao là 1,8 m. Tính thể tích của lều trại đó.

Lời giải:

Thể tích của phần dưới lều trại có dạng hình lập phương cạnh là 3 m là:

V₁ = 3³ = 27 (m³).

Thể tích của phần trên có dạng hình chóp tứ giác đều là:

$V_2=\frac{1}{3}{.3}^2\mathrm{.1,8}=\mathrm{5,4}\left(m^3\right)$.

Thể tích của lều trại đó là:

V = V₁ + V₂ = 27 + 5,4 = 32,4 (m³).

Lời giải bài tập Toán 8 Bài tập cuối chương 4 hay, chi tiết khác:

Sách bài tập Toán 8 Cánh diều Bài tập cuối chương 4

Với giải sách bài tập Toán 8 Bài tập cuối chương 4 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 8 Bài tập cuối chương 4.

Giải SBT Toán 8 Bài tập cuối chương 4 - Cánh diều

Tổng hợp Lý thuyết Toán 8 Chương 4 Cánh diều

Tổng hợp lý thuyết Toán 8 Chương 4: Hình học trực quan sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Tổng hợp Lý thuyết Toán 8 Chương 4 Cánh diều

Lý thuyết Tổng hợp Lý thuyết Toán 8 Chương 4

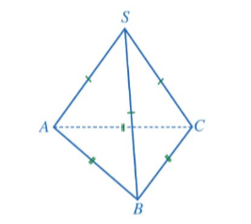
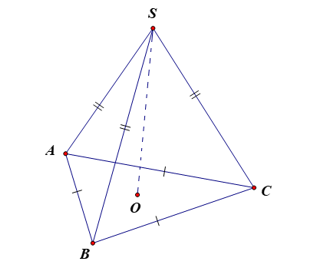
1. Hình chóp tam giác đều

- Hình chóp tam giác đều S.ABC;

- Mặt đáy ABC là một tam giác đều;

- Các mặt bên SAB, SBC, SCA là những tam giác cân tại S;

- Các cạnh đáy AB, BC, CA bằng nhau;

- Các cạnh bên SA, SB, SC bằng nhau;

- S gọi là đỉnh của hình chóp tam giác đều S.ABC.

Chú ý: Hình chóp tam giác đều có 4 mặt, 6 cạnh.

2. Diện tích xung quanh của hình chóp tam giác đều

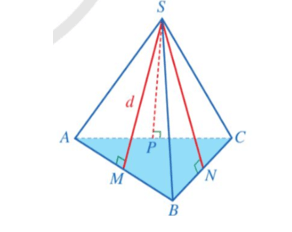
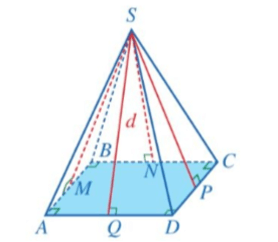
2.1. Trung đoạn của hình chóp tam giác đều

Cho hình chóp tam giác đều S.ABC. Gọi SM, SN, SP lần lượt là đường cao của các tam giác SAB, SBC, SCA. Mỗi đoạn thẳng SM, SN, SP đều được gọi là trung đoạn của hình chóp tam giác đều S.ABC.

2.2. Công thức tính diện tích xung quanh của hình chóp tam giác đều

Công thức tính

Diện tích xung quanh của hình chóp tam giác đều bằng nửa tích của chu vi đáy với độ dài trung đoạn.

Tức là:

$S_{xq}=\frac{1}{2}.C.d$, trong đó S_xq là diện tích xung quanh, C là chu vi đáy, d là độ dài trung đoạn của hình chóp tam giác đều.

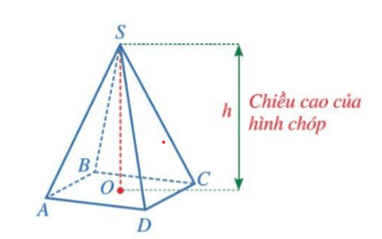
3. Thể tích của hình chóp tam giác đều

Cách tính

Thể tích của hình chóp tam giác đều bằng một phần ba tích của diện tích đáy với chiều cao.

Tức là:

$V=\frac{1}{3}.S.h$, trong đó V là thể tích, S là diện tích đáy, h là chiều cao của hình chóp tam giác đều.

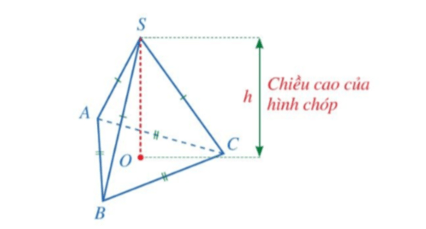
4. Hình chóp tứ giác đều

- Hình chóp tứ giác đều S.ABCD;

- Mặt đáy ABCD là một hình vuông;

- Các mặt bên SAB, SBC, SCD, SDA là những tam giác cân tại S;

- Các cạnh đáy AB, BC, CD, DA bằng nhau;

- Các cạnh bên SA, SB, SC, SD bằng nhau;

- Gọi S là đỉnh của hình chóp tứ giác đều S.ABCD.

Chú ý:

Hình chóp tứ giác đều có 5 mặt, 8 cạnh.

5. Diện tích xung quanh của hình chóp tứ giác đều

5.1. Trung đoạn của hình chóp tứ giác đều

Cho hình chóp tứ giác đều S.ABCD. Gọi SM, SN, SP, SQ lần lượt là đường cao của các tam giác SAB, SBC, SCD, SDA. Mỗi đoạn thẳng SM, SN, SP, SQ đều được gọi là trung đoạn của hình chóp tứ giác đều S.ABCD.

5.2. Công thức tính diện tích xung quanh của hình chóp tứ giác đều

Cách tính:

Diện tích xung quanh của hình chóp tứ giác đều bằng nửa tích của chu vi đáy với độ dài trung đoạn.

Tức là:

$S_{xq}=\frac{1}{2}.C.d$, trong đó S_xq là diện tích xung quanh, C là chu vi đáy, d là độ dài trung đoạn của hình chóp tứ giác đều.

6. Thể tích của hình chóp tứ giác đều

Cách tính:

Thể tích của hình chóp tứ giác đều bằng một phần ba tích của diện tích đáy với chiều cao.

Tức là:

$V=\frac{1}{3}.S.h$, trong đó V là thể tích, S là diện tích đáy, h là chiều cao của hình chóp tứ giác đều.

Bài tập Tổng hợp Lý thuyết Toán 8 Chương 4

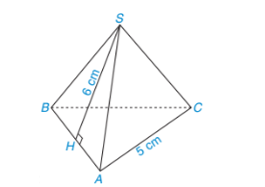
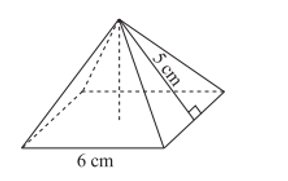
Bài 1: Tính diện tích xung quanh của hình chóp đều S.ABC như hình vẽ bên dưới

Hướng dẫn giải

Nửa chu vi đáy của hình chóp tam giác đều là: $\frac{1}{2}.\left(5+5+5\right)=\frac{15}{2}$  (cm).

Trung đoạn của hình chóp tam giác đều là: d = SH = 6 cm.

Diện tích xung quanh của hình chóp tam giác đều là: $S_{xq}=\frac{15}{2}.6=45$  (cm²).

Vậy diện tích xung quanh của hình chóp tam giác đều là 45 cm².

Bài 2: Một hình chóp tam giác đều S.ABC có diện tích đáy ABC là 27 cm² và chiều cao SO là 8cm. Tính thể tích của hình chóp tam giác đều S.ABC?

Hướng dẫn giải

Thể tích của hình chóp tam giác đều đó là: $V=\frac{1}{3}.27.8=72$  (cm³).

Vậy thể tích của hình chóp tam giác đều đó là 72 cm³.

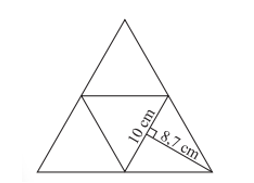
Bài 3: Nhân dịp tết trung thu, Nam dự định làm một chiếc lồng đèn hình chóp tam giác đều. Chiếc đèn lồng được làm bằng một tấm bìa như hình bên dưới biết rằng các mặt đều là hình tam giác đều. Em hãy giúp Nam tính xem phải cần bao nhiêu mét vuông giấy vừa đủ để dán tất cả các mặt của chiếc đèn lồng. Biết rằng nếp gấp không đáng kể? (lấy $\sqrt{3}\approx 1,7$ ).

Hướng dẫn giải

Chu vi đáy của chiếc đèn lồng là: 10.3 = 30 (cm).

Diện tích xung quanh của chiếc đèn lồng là: $S_{xq}=\frac{1}{2}.30.8,7=130,5$  (cm²).

Diện tích mặt đáy của chiếc đèn lồng là: $S={10}^2.\frac{\sqrt{3}}{4}\approx 42,5$  (cm²).

Diện tích giấy dán chiếc đèn lồng là: 130,5 + 42,5 = 173 (cm²).

Vậy diện tích giấy dán chiếc đèn lồng là 173 cm².

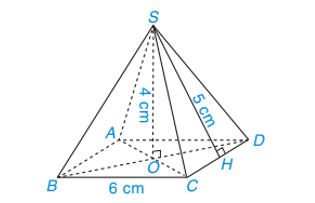
Bài 4: Một hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 6 cm, độ dài trung đoạn bằng 5 cm và chiều cao bằng 4 cm.

a) Tính diện tích xung quanh của hình chóp tứ giác đều đó?

b) Tính thể tích của hình chóp tứ giác đều đó?

Hướng dẫn giải

a) Chu vi đáy của hình chóp tứ giác đều là: 6.4 = 24 (cm).

Diện tích xung quanh của hình chóp tứ giác đều là: $S_{xq}=\frac{1}{2}\mathrm{.24.5}=60$  (cm²).

Vậy diện tích xung quanh của hình chóp tứ giác đều là 60 cm².

b) Diện tích đáy của hình chóp tứ giác đều là: 6.6 = 36 (cm²).

Thể tích của hình chóp tứ giác đều là: $V=\frac{1}{3}.36.4=48$ (cm³).

Thể tích của hình chóp tứ giác đều là 48 cm³.

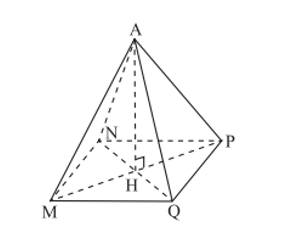
Bài 5: Tính chiều cao AH của hình chóp tứ giác đều A.MNPQ biết độ dài cạnh đáy hình vuông MNPQ là 8cm và thể tích của hình chóp tứ giác đều đó là 192 cm³?

Hướng dẫn giải

Diện tích đáy MNPQ là: S = 8.8 = 64 (cm²).

Độ dài chiều cao AH là: $\frac{3.V_{A.MNPQ}}{S}=\frac{3.192}{64}=9$  (cm).

Vậy độ dài chiều cao AH là 9 cm.

Bài 6: Bác Khôi làm một chiếc hộp gỗ có dạng hình chóp tứ giác đều với độ dài cạnh đáy của hình chóp là 6 m, trung đoạn của hình chóp là 5 m. Bác Khôi muốn sơn bốn mặt xung quanh của hộp gỗ. Cứ mỗi mét vuông sơn cần trả 30 000 đồng (tiền sơn và tiền công). Hỏi bác Khôi phải trả chi phí là bao nhiêu?

Hướng dẫn giải

Chu vi đáy của chiếc hộp là: 6.4 = 24 (m).

Diện tích xung quanh của chiếc hộp là: $S_{xq}=\frac{1}{2}.24.5=60$  (m²).

Diện tích sơn chính là diện tích xung quanh của chiếc hộp.

Do đó số tiền bác Khôi phải trả là: 60 . 30 000 = 1 800 000 (đồng).

Vậy số tiền bác Khôi phải trả là 1 800 000 đồng.

Học tốt Toán 8 Chương 4

Các bài học để học tốt tổng hợp Toán 8 Chương 4 Toán lớp 8 hay khác:

30 Bài tập tổng hợp Toán 8 Chương 4 Kết nối tri thức có lời giải

Với 30 bài tập trắc nghiệm tổng hợp Toán lớp 8 Chương 4: Hình học trực quan có đáp án và lời giải chi tiết đầy đủ các mức độ sách Cánh diều sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 8.

30 Bài tập tổng hợp Toán 8 Chương 4 Kết nối tri thức có lời giải

Nội dung đang được cập nhật ...

Xem thêm bài tập trắc nghiệm Toán lớp 8 Cánh diều có đáp án hay khác: