Với giải bài tập Toán 8 Bài tập cuối chương 8 sách Cánh diều hay nhất, chi tiết giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8.

Giải Toán 8 Cánh diều Bài tập cuối chương 8

Giải Toán 8 trang 94

Bài tập

Bài 1 trang 94 Toán 8 Tập 2 Cánh diều

Giải Toán 8 Bài tập cuối chương 8 - Cánh diều

Bài 1 trang 94 Toán 8 Tập 2: Cho ∆DEG ᔕ ∆MNP, $\hat{E}=60°,$ $\hat{M}=40°.$

a) Số đo góc D bằng bao nhiêu độ?

A. 40°.       

B. 50°.       

C. 60°.       

D. 80°.

b) Số đo góc N bằng bao nhiêu độ?

A. 40°.       

B. 50°.       

C. 60°.       

D. 80°.

c) Số đo góc P bằng bao nhiêu độ?

A. 40°.       

B. 50°.       

C. 60°.       

D. 80°.

Lời giải:

a) Đáp án đúng là: A

Vì ∆DEG ᔕ ∆MNP nên $\hat{D}=\hat{M}=40°$  (hai góc tương ứng).

b) Đáp án đúng là: C    

Vì ∆DEG ᔕ ∆MNP nên $\hat{E}=\hat{N}$  (hai góc tương ứng).

Do đó $\hat{N}=\hat{E}=60°.$

c) Đáp án đúng là: D

Xét tam giác MNP có $\hat{M}+\hat{N}+\hat{P}=180°$  (tổng ba góc của một tam giác)

Suy ra $\hat{P}=180°-\left(\hat{M}+\hat{N}\right)=180°-\left(40°+60°\right)=80°.$

Lời giải bài tập Toán 8 Bài tập cuối chương 8 hay, chi tiết khác:

Bài 2 trang 94 Toán 8 Tập 2 Cánh diều

Giải Toán 8 Bài tập cuối chương 8 - Cánh diều

Bài 2 trang 94 Toán 8 Tập 2: Cho ∆DEG ᔕ ∆MNP, DE = 2 cm, DG = 4 cm, MN = 4 cm, NP = 6 cm.

a) Độ dài cạnh EG là

A. 2 cm.     

B. 3 cm.     

C. 4 cm.     

D. 8 cm.

b) Độ dài cạnh MP là

A. 2 cm.     

B. 3 cm.     

C. 4 cm.     

D. 8 cm.

Lời giải:

Đáp án đúng là: B

a) Vì ∆DEG ᔕ ∆MNP nên $\frac{\mathrm{DE}}{\mathrm{MN}}=\frac{\mathrm{EG}}{\mathrm{NP}}$  (tỉ số đồng dạng)

Hay $\frac{2}{4}=\frac{\mathrm{EG}}{6}$

Suy ra $\mathrm{EG}=\frac{2\cdot 6}{4}=3$  (cm).

b) Đáp án đúng là: D

Vì ∆DEG ᔕ ∆MNP nên $\frac{\mathrm{DE}}{\mathrm{MN}}=\frac{\mathrm{DG}}{\mathrm{MP}}$  (tỉ số đồng dạng)

Hay $\frac{2}{4}=\frac{4}{\mathrm{MP}}$

Suy ra $\mathrm{MP}=\frac{4\cdot 4}{2}=8$  (cm).

Lời giải bài tập Toán 8 Bài tập cuối chương 8 hay, chi tiết khác:

Bài 3 trang 94 Toán 8 Tập 2 Cánh diều

Giải Toán 8 Bài tập cuối chương 8 - Cánh diều

Bài 3 trang 94 Toán 8 Tập 2: Cho tam giác ABC, các điểm M, N, P lần lượt thuộc các cạnh AB, AC, BC sao cho tứ giác BMNP là hình bình hành (Hình 102). Chứng minh rằng $\frac{\mathrm{MN}}{\mathrm{BC}}+\frac{\mathrm{NP}}{\mathrm{AB}}=1.$

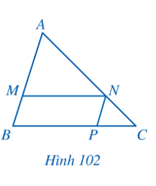
Lời giải:

Vì BMNP là hình bình hành nên NP = MB và MN // BP.

Xét ∆ABC với MN // BC, ta có $\frac{\mathrm{MN}}{\mathrm{BC}}=\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AC}}$  (hệ quả của định lí Thalès)

Suy ra $\frac{\mathrm{MN}}{\mathrm{BC}}+\frac{\mathrm{NP}}{\mathrm{AB}}=\frac{\mathrm{AM}}{\mathrm{AB}}+\frac{\mathrm{NP}}{\mathrm{AB}}=\frac{\mathrm{AM}}{\mathrm{AB}}+\frac{\mathrm{MB}}{\mathrm{AB}}=\frac{\mathrm{AM}+\mathrm{MB}}{\mathrm{AB}}=\frac{\mathrm{AB}}{\mathrm{AB}}=1$ .

Vậy $\frac{\mathrm{MN}}{\mathrm{BC}}+\frac{\mathrm{NP}}{\mathrm{AB}}=1.$

Lời giải bài tập Toán 8 Bài tập cuối chương 8 hay, chi tiết khác:

Bài 4 trang 94 Toán 8 Tập 2 Cánh diều

Giải Toán 8 Bài tập cuối chương 8 - Cánh diều

Bài 4 trang 94 Toán 8 Tập 2: Cho tứ giác ABCD. Tia phân giác của góc BAD và BCD cắt nhau tại điểm I (Hình 103). Chứng minh AB.CD = AD.BC.

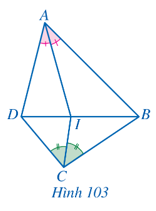
Lời giải:

Xét ∆ABD có AI là phân giác của góc BAD nên $\frac{\mathrm{IB}}{\mathrm{ID}}=\frac{\mathrm{AB}}{\mathrm{AD}}$  (tính chất đường phân giác)

Xét ∆BCD có CI là phân giác của góc BCD nên $\frac{\mathrm{IB}}{\mathrm{ID}}=\frac{\mathrm{CB}}{\mathrm{CD}}$  (tính chất đường phân giác)

Suy ra $\frac{\mathrm{AB}}{\mathrm{AD}}=\frac{\mathrm{CB}}{\mathrm{CD}},$  do đó AB.CD = AD.BC.

Lời giải bài tập Toán 8 Bài tập cuối chương 8 hay, chi tiết khác:

Bài 5 trang 94 Toán 8 Tập 2 Cánh diều

Giải Toán 8 Bài tập cuối chương 8 - Cánh diều

Bài 5 trang 94 Toán 8 Tập 2: Cho hình bình hành ABCD. Gọi M, N, P lần lượt là trung điểm các đoạn thẳng AB, BC, AN và Q là giao điểm của AN và DM. Chứng minh:

a) MP // AD, $\mathrm{MP}=\frac{1}{4}\mathrm{AD};$

b) $\mathrm{AQ}=\frac{2}{5}\mathrm{AN};$

c) Gọi R là trung điểm của CD. Chứng minh ba điểm M, P, R thẳng hàng và  $\mathrm{PR}=\frac{3}{4}\mathrm{AD}.$  

Lời giải:

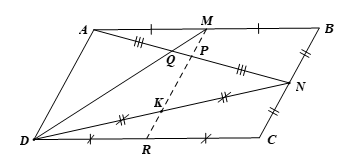
a)  Do N là trung điểm của BC nên $\mathrm{BN}=\frac{1}{2}\mathrm{BC}$

Và ABCD là hình bình hành nên BC = AD, BC // AD

Suy ra  $\mathrm{BN}=\frac{1}{2}\mathrm{AD},\mathrm{BN}\text{ // }\mathrm{AD}$ (1)

Xét ∆ABN có M, P lần lượt là trung điểm của AB, AN nên MP là đường trung bình của ∆ABN

Suy ra $\mathrm{MP}=\frac{1}{2}\mathrm{BN}$  và MP // BN         (2)

Từ (1) và (2) ta có $\mathrm{MP}=\frac{1}{2}\mathrm{BN}=\frac{1}{2}\cdot \frac{1}{2}\mathrm{AD}=\frac{1}{4}\mathrm{AD}$  và MP // AD.

Vậy MP // AD và $\mathrm{MP}=\frac{1}{4}\mathrm{AD}.$  (3)

b) Xét ∆ADQ với MP // AD, ta có $\frac{\mathrm{AD}}{\mathrm{MP}}=\frac{\mathrm{QA}}{\mathrm{QP}}$  (hệ quả của định lí Thalès)

Hay $\frac{\mathrm{AD}}{\frac{1}{4}\mathrm{AD}}=\frac{\mathrm{AQ}}{\mathrm{PQ}}$  nên $\frac{\mathrm{AQ}}{\mathrm{PQ}}=\frac{4}{1}$

Suy ra $\frac{\mathrm{AQ}}{\mathrm{PQ}+\mathrm{AQ}}=\frac{4}{1+4}$  hay $\frac{\mathrm{AQ}}{\mathrm{AP}}=\frac{4}{5}$

Mà P là trung điểm của AN nên $\mathrm{AP}=\frac{1}{2}\mathrm{AN}$

Do đó $\frac{\mathrm{AQ}}{\frac{1}{2}\mathrm{AN}}=\frac{4}{5},$  suy ra $\mathrm{AQ}=\frac{4}{5}\cdot \frac{1}{2}\mathrm{AN}=\frac{2}{5}\mathrm{AN}.$

Vậy $\mathrm{AQ}=\frac{2}{5}\mathrm{AN}.$

c) Gọi K là trung điểm của DN.

Xét ∆AND có P, K lần lượt là trung điểm của AN, DN nên PK là đường trung bình của ∆AND. Do đó PK // AD và $\mathrm{PK}=\frac{1}{2}\mathrm{AD}$    (4)

Tương tự, xét ∆CDN có KR là đường trung bình của ∆CDN nên KR // CN và $\mathrm{KR}=\frac{1}{2}\mathrm{CN}$    

Mà N là trung điểm của BC nên $\mathrm{CN}=\frac{1}{2}\mathrm{BC}=\frac{1}{2}\mathrm{AD}$  và BC // AD

Do đó KR // AD và $\mathrm{KR}=\frac{1}{2}\mathrm{CN}=\frac{1}{2}\cdot \frac{1}{2}\mathrm{AD}=\frac{1}{4}\mathrm{AD}$  (5)

Từ (3), (4) và (5), theo tiên đề Euclid ta có: M, P, K, R thẳng hàng.

Và $\mathrm{PR}=\mathrm{PK}+\mathrm{KR}=\frac{1}{2}\mathrm{AD}+\frac{1}{4}\mathrm{AD}=\frac{3}{4}\mathrm{AD}.$

Vậy ba điểm M, P, R thẳng hàng và $\mathrm{PR}=\frac{3}{4}\mathrm{AD}.$

Lời giải bài tập Toán 8 Bài tập cuối chương 8 hay, chi tiết khác:

Bài 6 trang 95 Toán 8 Tập 2 Cánh diều

Giải Toán 8 Bài tập cuối chương 8 - Cánh diều

Bài 6 trang 95 Toán 8 Tập 2: Cho ∆ABC ᔕ ∆A’B’C’ với tỉ số đồng dạng k.

a) Gọi AM, AM’ lần lượt là các đường trung tuyến của ∆ABC và ∆A’B’C’. Chứng minh ∆ABM ᔕ ∆A’B’M’ và $\frac{\mathrm{AM}}{A^{\text{'}}{M}^{\text{'}}}=k.$

b) Gọi AD, AD’ lần lượt là các đường phân giác của ∆ABC và ∆A’B’C’.

Chứng minh ∆ABD ᔕ ∆A’B’D’ và $\frac{\mathrm{AD}}{A^{\text{'}}{D}^{\text{'}}}=k.$

c) Gọi AH, AH’ lần lượt là các đường cao của các tam giác nhọn ABC, A’B’C’. Chứng minh ∆ABH ᔕ ∆A’B’H’ và $\frac{\mathrm{AH}}{A^{\text{'}}{H}^{\text{'}}}=k.$

Lời giải:

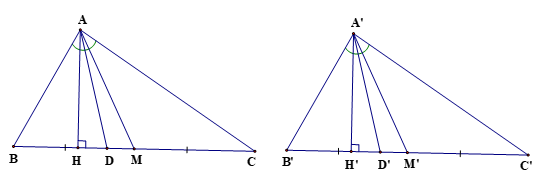
Vì ∆ABC ᔕ ∆A’B’C’với tỉ số đồng dạng k nên ta có:

$\frac{\mathrm{AB}}{A^{\text{'}}{B}^{\text{'}}}=\frac{\mathrm{BC}}{B^{\text{'}}{C}^{\text{'}}}=\frac{\mathrm{AC}}{A^{\text{'}}{C}^{\text{'}}}=k$ và $\widehat{\mathrm{BAC}}=\widehat{B^{\text{'}}{A}^{\text{'}}{C}^{\text{'}}},\hat{B}=\widehat{B^{\text{'}}},\hat{C}=\widehat{C^{\text{'}}}.$

a) Vì M, M’ lần lượt là trung điểm của BC, B’C’ nên $\mathrm{BM}=\frac{1}{2}\mathrm{BC}$  và $B^{\text{'}}{M}^{\text{'}}=\frac{1}{2}{B}^{\text{'}}{C}^{\text{'}}$

Suy ra $\frac{\mathrm{AB}}{A^{\text{'}}{B}^{\text{'}}}=\frac{\mathrm{BC}}{B^{\text{'}}{C}^{\text{'}}}=\frac{\mathrm{BM}}{B^{\text{'}}{M}^{\text{'}}}=k$

Xét ∆ABM và ∆A’B’M’ có: $\frac{\mathrm{AB}}{A^{\text{'}}{B}^{\text{'}}}=\frac{\mathrm{BM}}{B^{\text{'}}{M}^{\text{'}}}=k$  và $\hat{B}=\widehat{B^{\text{'}}}$

Suy ra ∆ABM ᔕ ∆A’B’M’ (c.g.c)

Do đó $\frac{\mathrm{AM}}{A^{\text{'}}{M}^{\text{'}}}=\frac{\mathrm{AB}}{A^{\text{'}}{B}^{\text{'}}}=k$  (tỉ số đồng dạng).

b) Vì AD, AD’ lần lượt là các đường phân giác của tam giác ABC, A’B’C’ nên $\widehat{\mathrm{BAD}}=\frac{1}{2}\widehat{\mathrm{BAC}}$  và $\widehat{B^{\text{'}}{A}^{\text{'}}{D}^{\text{'}}}=\frac{1}{2}\widehat{B^{\text{'}}{A}^{\text{'}}{C}^{\text{'}}}$

Mà $\widehat{\mathrm{BAC}}=\widehat{B^{\text{'}}{A}^{\text{'}}{C}^{\text{'}}}$  nên $\widehat{\mathrm{BAD}}=\widehat{B^{\text{'}}{A}^{\text{'}}{D}^{\text{'}}}$

Xét ∆ABD và ∆A’B’D’ có: $\widehat{\mathrm{BAD}}=\widehat{B^{\text{'}}{A}^{\text{'}}{D}^{\text{'}}}$  và $\hat{B}=\widehat{B^{\text{'}}}$

Do đó ∆ABD ᔕ ∆A’B’D’ (g.g) 

Suy ra $\frac{\mathrm{AD}}{A^{\text{'}}{D}^{\text{'}}}=\frac{\mathrm{AB}}{A^{\text{'}}{B}^{\text{'}}}=k$  (tỉ số đồng dạng).

c) Vì AH, AH’ lần lượt là các  đường cao của tam giác ABC, A’B’C’ nên $\widehat{\mathrm{AHB}}=\widehat{A^{\text{'}}{H}^{\text{'}}{B}^{\text{'}}}=90°$

Xét ∆ABH và ∆A’B’H’ có: $\widehat{\mathrm{AHB}}=\widehat{A^{\text{'}}{H}^{\text{'}}{B}^{\text{'}}}=90°$  và $\hat{B}=\widehat{B^{\text{'}}}$

Do đó ∆ABH ᔕ ∆A’B’H’ (g.g)

Suy ra $\frac{\mathrm{AH}}{A^{\text{'}}{H}^{\text{'}}}=\frac{\mathrm{AB}}{A^{\text{'}}{B}^{\text{'}}}=k$  (tỉ số đồng dạng).

Lời giải bài tập Toán 8 Bài tập cuối chương 8 hay, chi tiết khác:

Bài 7 trang 95 Toán 8 Tập 2 Cánh diều

Giải Toán 8 Bài tập cuối chương 8 - Cánh diều

Bài 7 trang 95 Toán 8 Tập 2: Tính các độ dài x, y, z, t ở các hình 104a, 104b, 104c:

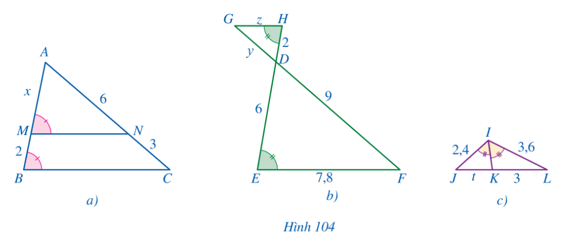
Lời giải:

+ Xét hình 104a:

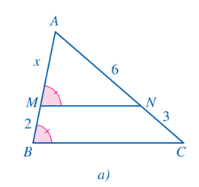
Theo hình vẽ ta có: $\widehat{\mathrm{AMN}}=\widehat{\mathrm{ABC}}$  mà hai góc ở vị trí đồng vị suy ra MN // BC.

Xét ∆ABC với MN // BC, ta có $\frac{\mathrm{AM}}{\mathrm{MB}}=\frac{\mathrm{AN}}{\mathrm{NC}}$  (định lí Thalès)

Hay $\frac{x}{2}=\frac{6}{3}$  nên $x=\frac{2\cdot 6}{3}=4.$

Vậy x = 4.

+ Xét hình 104b:

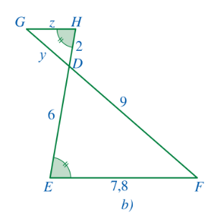
Theo hình vẽ ta có: $\widehat{\mathrm{GHD}}=\widehat{\mathrm{DEF}}$  mà hai góc ở vị trí so le trong nên GH // EF.

Xét ∆DEF với GH // EF, ta có $\frac{\mathrm{GH}}{\mathrm{EF}}=\frac{\mathrm{GD}}{\mathrm{DF}}=\frac{\mathrm{HD}}{\mathrm{DE}}$  (hệ quả của định lí Thalès)

Hay $\frac{z}{7,8}=\frac{y}{9}=\frac{2}{6}$

Suy ra $z=\frac{7,8\cdot 2}{6}=2,6$  và $y=\frac{9\cdot 2}{6}=3.$

Vậy y = 3 và z = 2,6.

+ Xét  hình 104c:

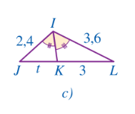
Theo hình vẽ ta có: $\widehat{\mathrm{JIK}}=\widehat{\mathrm{LIK}}$  nên IK là đường phân giác của góc JIL.

Xét ∆IJL có IK là đường phân giác của góc JIL nên $\frac{\mathrm{KJ}}{\mathrm{KL}}=\frac{\mathrm{IJ}}{\mathrm{IL}}$  (tính chất đường phân giác)

Hay $\frac{t}{3}=\frac{2,4}{3,6},$  suy ra $t=\frac{3\cdot 2,4}{3,6}=2.$

Vậy t = 2.

Lời giải bài tập Toán 8 Bài tập cuối chương 8 hay, chi tiết khác:

Bài 8 trang 95 Toán 8 Tập 2 Cánh diều

Giải Toán 8 Bài tập cuối chương 8 - Cánh diều

Bài 8 trang 95 Toán 8 Tập 2: Cho Hình 105. Chứng minh:

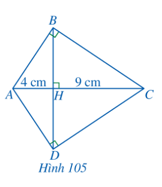
a) ∆HAB ᔕ ∆HBC;

b) HB = HD = 6 cm.

Lời giải:

a) Xét ∆HAB và ∆HBC có:

$\widehat{\mathrm{AHB}}=\widehat{\mathrm{BHC}}=90°;$ $\widehat{\mathrm{HAB}}=\widehat{\mathrm{HBC}}$  (cùng phụ với góc $\widehat{\mathrm{ABH}})$

Suy ra ∆HAB ᔕ ∆HBC (g.g)

b) Do ∆HAB ᔕ ∆HBC (câu a) nên $\frac{\mathrm{HA}}{\mathrm{HB}}=\frac{\mathrm{HB}}{\mathrm{HC}}$  (tỉ số đồng dạng)

Suy ra HB² = HA.HC = 4 . 9 = 36

Do đó HB = 6 cm.

Xét ∆HAD và ∆HDC có

$\widehat{\mathrm{AHD}}=\widehat{\mathrm{DHC}}=90°;$ $\widehat{\mathrm{HAD}}=\widehat{\mathrm{HDC}}$  (cùng phụ với góc $\widehat{\mathrm{ADH}})$

Do đó ∆HAD ᔕ ∆HDC (g.g)

Suy ra $\frac{\mathrm{HA}}{\mathrm{HD}}=\frac{\mathrm{HD}}{\mathrm{HC}}$  (tỉ số đồng dạng)

Nên HD² = HA.HC = 4 . 9 = 36

Do đó HD = 6 (cm).

Vậy HB = HD = 6 cm.

Lời giải bài tập Toán 8 Bài tập cuối chương 8 hay, chi tiết khác:

Bài 9 trang 95 Toán 8 Tập 2 Cánh diều

Giải Toán 8 Bài tập cuối chương 8 - Cánh diều

Bài 9 trang 95 Toán 8 Tập 2: Cho Hình 106. Chứng minh:

a) AH² = AB.AI = AC.AK;

b) $\widehat{\mathrm{AIK}}=\widehat{\mathrm{ACH}}.$

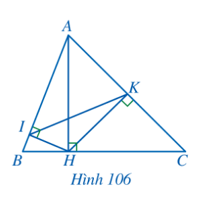
Lời giải:

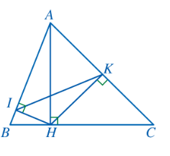
a) Xét ∆AHI và ∆ABH có:

$\widehat{\mathrm{AIH}}=\widehat{\mathrm{AHB}}=90°;$ $\widehat{\mathrm{BAH}}$  là góc chung

Suy ra ∆AHI ᔕ ∆ABH (g.g)

Do đó $\frac{\mathrm{AH}}{\mathrm{AB}}=\frac{\mathrm{AI}}{\mathrm{AH}}$  (tỉ số đồng dạng)

Nên AH² = AB.AI (1)

Xét ∆AHK và ∆ACH có:

$\widehat{\mathrm{AKH}}=\widehat{\mathrm{AHC}}=90°;$ $\widehat{\mathrm{HAC}}$  là góc chung

Suy ra ∆AHK ᔕ ∆ACH (g.g)

Do đó $\frac{\mathrm{AH}}{\mathrm{AC}}=\frac{\mathrm{AK}}{\mathrm{AH}}$  (tỉ số đồng dạng)

Nên AH² = AC.AK (2)

Từ (1) và (2), suy ra AH² = AB.AI = AC.AK.

b) Ta có: AB.AI = AC.AK (câu a) suy ra $\frac{\mathrm{AK}}{\mathrm{AB}}=\frac{\mathrm{AI}}{\mathrm{AC}}$

Xét ∆AIK và ∆ACB có:

$\widehat{\mathrm{BAC}}$ là góc chung; $\frac{\mathrm{AK}}{\mathrm{AB}}=\frac{\mathrm{AI}}{\mathrm{AC}}$ .

Suy ra ∆AIK ᔕ ∆ACB (c.g.c)

Do đó $\widehat{\mathrm{AIK}}=\widehat{\mathrm{ACB}}$  (hai góc tương ứng).

Vậy $\widehat{\mathrm{AIK}}=\widehat{\mathrm{ACH}}.$

Lời giải bài tập Toán 8 Bài tập cuối chương 8 hay, chi tiết khác:

Bài 10 trang 96 Toán 8 Tập 2 Cánh diều

Giải Toán 8 Bài tập cuối chương 8 - Cánh diều

Bài 10 trang 96 Toán 8 Tập 2: Cho tam giác ABC có M, N là hai điểm lần lượt thuộc các cạnh AB, AC sao cho MN // BC. Gọi I, P, Q lần lượt là giao điểm của BN và CM, AI và MN, AI và BC. Chứng minh:

a) $\frac{\mathrm{MP}}{\mathrm{BQ}}=\frac{\mathrm{PN}}{\mathrm{QC}}=\frac{\mathrm{AP}}{\mathrm{AQ}};$                 

b) $\frac{\mathrm{MP}}{\mathrm{QC}}=\frac{\mathrm{PN}}{\mathrm{BQ}}=\frac{\mathrm{IP}}{\mathrm{IQ}}.$

Lời giải:

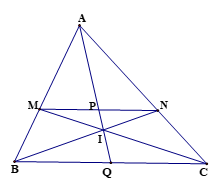
a) Vì MN // BC, P ∈ MN nên ta có: MP // BQ, PN // QC.

Xét ∆ABQ với MP // BQ, ta có: $\frac{\mathrm{MP}}{\mathrm{BQ}}=\frac{\mathrm{AP}}{\mathrm{AQ}}$  (hệ quả của định lí Thalès)

Xét ∆AQC với PN // QC, ta có: $\frac{\mathrm{PN}}{\mathrm{QC}}=\frac{\mathrm{AP}}{\mathrm{AQ}}$  (hệ quả của định lí Thalès)

Suy ra $\frac{\mathrm{MP}}{\mathrm{BQ}}=\frac{\mathrm{PN}}{\mathrm{QC}}=\frac{\mathrm{AP}}{\mathrm{AQ}}.$

b) Vì MN // BC nên ta có: MP // QC, PN // BQ.

Xét ∆CQI với MP // QC, ta có: $\frac{\mathrm{MP}}{\mathrm{QC}}=\frac{\mathrm{IP}}{\mathrm{IQ}}$  (hệ quả của định lí Thalès)

Xét ∆BQI với PN // BQ, ta có: $\frac{\mathrm{PN}}{\mathrm{BQ}}=\frac{\mathrm{IP}}{\mathrm{IQ}}$  (hệ quả của định lí Thalès)

Suy ra $\frac{\mathrm{MP}}{\mathrm{QC}}=\frac{\mathrm{PN}}{\mathrm{BQ}}=\frac{\mathrm{IP}}{\mathrm{IQ}}.$

Lời giải bài tập Toán 8 Bài tập cuối chương 8 hay, chi tiết khác:

Bài 11 trang 96 Toán 8 Tập 2 Cánh diều

Giải Toán 8 Bài tập cuối chương 8 - Cánh diều

Bài 11 trang 96 Toán 8 Tập 2: Cho Hình 107. Chứng minh:

a) ∆ABN ᔕ ∆AIP và AI.AN = AP.AB;

b) AI.AN + BI.BM = AB².

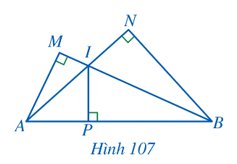
Lời giải:

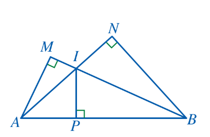
a) Xét ∆ABN và ∆AIP có:

$\widehat{\mathrm{ANB}}=\widehat{\mathrm{API}}=90°;$ $\widehat{\mathrm{IAP}}$  là góc chung

Suy ra ∆ABN ᔕ ∆AIP (g.g)

Do đó $\frac{\mathrm{AB}}{\mathrm{AI}}=\frac{\mathrm{AN}}{\mathrm{AP}}$  (tỉ số đồng dạng)

Nên AI.AN = AP.AB.     (1)

b) Xét ∆ABM và ∆IBP có:

$\widehat{\mathrm{AMB}}=\widehat{\mathrm{IPB}}=90°;$ $\widehat{\mathrm{ABM}}$  là góc chung

Suy ra ∆ABM ᔕ ∆IBP (g.g)

Do đó $\frac{\mathrm{AB}}{\mathrm{IB}}=\frac{\mathrm{BM}}{\mathrm{BP}}$  (tỉ số đồng dạng)

Nên AB.BP = BI.BM (2)

Từ (1) và (2) suy ra

AI.AN + BI.BM = AB.AP + AB.BP

                          = AB.(AP + BP) = AB.AB = AB².

Vậy AI.AN + BI.BM = AB².

Lời giải bài tập Toán 8 Bài tập cuối chương 8 hay, chi tiết khác:

Bài 12 trang 96 Toán 8 Tập 2 Cánh diều

Giải Toán 8 Bài tập cuối chương 8 - Cánh diều

Bài 12 trang 96 Toán 8 Tập 2: Hình 108 minh họa mặt cắt đứng của tủ sách nghệ thuật ở nhà bác Ngọc. Sau một thời gian sử dụng, tủ sách đó đã có dấu hiệu bị xuống cấp và cần sửa lại. Các tấm ngăn BM, CN, DP bị hỏng và cần thay mới. Em hãy giúp bác Ngọc tính toán chiều dài các tấm ngăn mới lần lượt thay thế cho các tấm ngăn BM, CN, DP đã bị hỏng. Biết chiều dài tấm ngăn EQ bằng 4 m.

Lời giải:

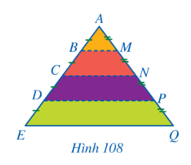
Ta có: AB = BC = CD = DE (giả thiết);

          AC = AB + BC; CE = CD + DE

Suy ra AC = CE hay C là trung điểm của AE.

Lại có: AM = MN = NP = PQ (giả thiết);

           AN = AM + MN; NQ = NP + PQ

Suy ra AN = NQ hay N là trung điểm của AQ.

⦁ Xét ∆AEQ có C, N lần lượt là trung điểm của AE, AQ nên CN là đường trung bình của ∆AEQ

Suy ra $\mathrm{CN}=\frac{1}{2}\mathrm{EQ}=\frac{1}{2}\cdot 4=2$  (m).

⦁ Xét ∆ACN có B, M lần lượt là trung điểm của AC, AN (do AB = BC và AM = MN) nên BM là đường trung bình của ∆ACN.

Do đó $\mathrm{BM}=\frac{1}{2}\mathrm{CN}=\frac{1}{2}\cdot 2=1$  (m).

⦁ Ta có: AD = AB + BC + CD = 3AB, nên $\frac{\mathrm{AB}}{\mathrm{AD}}=\frac{1}{3}.$

            AP = AM + MN + NP = 3AM, nên $\frac{\mathrm{AM}}{\mathrm{AP}}=\frac{1}{3}.$

Do đó $\frac{\mathrm{AB}}{\mathrm{AD}}=\frac{\mathrm{AM}}{\mathrm{AP}}=\frac{1}{3}.$

Xét ∆ADP có $\frac{\mathrm{AB}}{\mathrm{AD}}=\frac{\mathrm{AM}}{\mathrm{AP}}$  nên BM // DP (định lí Thalès đảo)

Suy ra  (hệ quả của định lí Thalès)

Do đó DP = 3BM = 3.1 = 3 (m).

Vậy BM = 1 m, CN = 2 m, DP = 3 m.

Lời giải bài tập Toán 8 Bài tập cuối chương 8 hay, chi tiết khác:

Bài 13 trang 96 Toán 8 Tập 2 Cánh diều

Giải Toán 8 Bài tập cuối chương 8 - Cánh diều

Bài 13 trang 96 Toán 8 Tập 2: Cho Hình 109. Hình nào đồng dạng phối cảnh với:

a) Tam giác OAB?                                      b) Tam giác OBC?

c) Tam giác OCD?                                      d) Tứ giác ABCD?

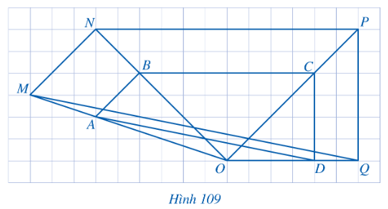
Lời giải:

a) Ta thấy hai đường thẳng AM, BN cùng đi qua điểm O và $\frac{\mathrm{OM}}{\mathrm{OA}}=\frac{\mathrm{ON}}{\mathrm{OB}}$  nên tam giác OMN đồng dạng phối cảnh với tam giác OAB.

Tương tự như vậy, ta cũng có hình đồng dạng phối cảnh với:

b) Tam giác OBC là: tam giác ONP.

c) Tam giác OCD là: tam giác OPQ.

d) Tứ giác ABCD là: Tứ giác MNPQ.

Lời giải bài tập Toán 8 Bài tập cuối chương 8 hay, chi tiết khác:

Bài 14 trang 96 Toán 8 Tập 2 Cánh diều

Giải Toán 8 Bài tập cuối chương 8 - Cánh diều

Bài 14 trang 96 Toán 8 Tập 2: Hình 110 có ghi thứ tự của 6 lá mầm, trong đó có nhiều cặp lá mầm gợi nên những cặp hình đồng dạng. Hãy viết 6 cặp lá mầm gợi nên những hình đồng dạng.

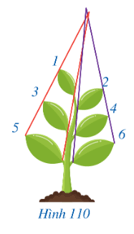
Lời giải:

Cặp 1: Lá mầm 1 và 3;

Cặp 2: Lá mầm 3 và 5;

Cặp 3: Lá mầm 1 và 5;

Cặp 4: Lá mầm 2 và 4;

Cặp 5: Lá mầm 4 và 6;

Cặp 6: Lá mầm 2 và 6.

Lời giải bài tập Toán 8 Bài tập cuối chương 8 hay, chi tiết khác: