Với giải bài tập Toán 8 Bài 11: Hình thang cân sách Kết nối tri thức hay nhất, chi tiết giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 Bài 11.

Giải Toán 8 Kết nối tri thức Bài 11: Hình thang cân

Video Giải Toán 8 Bài 11: Hình thang cân - Cô Vũ Chuyên (Giáo viên VietJack)

Mở đầu trang 52 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 11: Hình thang cân - Kết nối tri thức

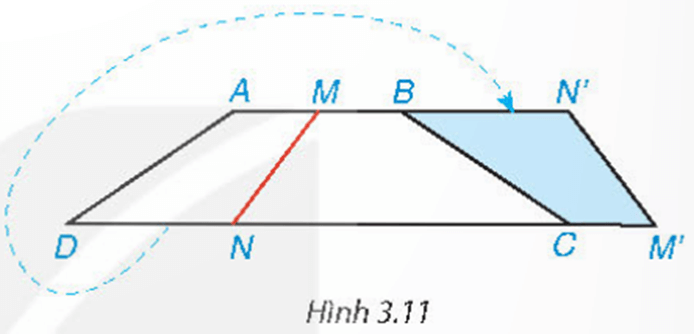
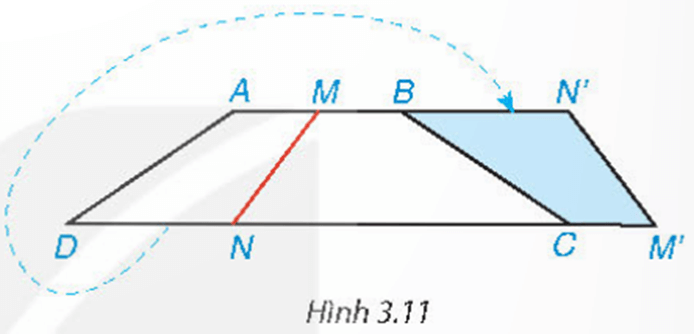
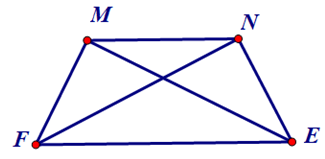
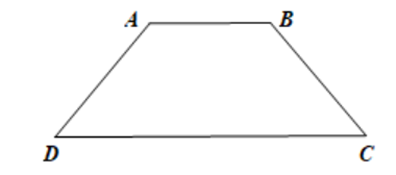
Mở đầu trang 52 Toán 8 Tập 1: Cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy thì được hai hình thang. Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu (Hình 3.11). Hãy giải thích tại sao hình tạo thành cũng là một hình thang cân.

Lời giải:

Sau bài học này ta giải quyết được bài toán như sau:

Ta cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy.

Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu nên $\widehat{AMN}=\widehat{M^{\text{'}}}$ (1)

Tứ giác ABCD là hình thang cân có AB // CD

Mà theo cách ghép thì chỗ ghép ở các đỉnh M, B tạo thành đường thẳng AN’, chỗ ghép ở các đỉnh N, C tạo thành đường thẳng DM’. Do đó AN’ // M’D.

Suy ra $\widehat{AMN}=\widehat{MN{M}^{\text{'}}}$ (so le trong) (2)

Từ (1) và (2) suy ra $\widehat{MN{M}^{\text{'}}}=\widehat{M^{\text{'}}}$ .

Xét tứ giác MN’M’N có MN’ // M’N nên là hình thang.

Lại có $\widehat{MN{M}^{\text{'}}}=\widehat{M^{\text{'}}}$ nên MN’M’N là hình thang cân.

Lời giải bài tập Toán 8 Bài 11: Hình thang cân hay, chi tiết khác:

Luyện tập 1 trang 53 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 11: Hình thang cân - Kết nối tri thức

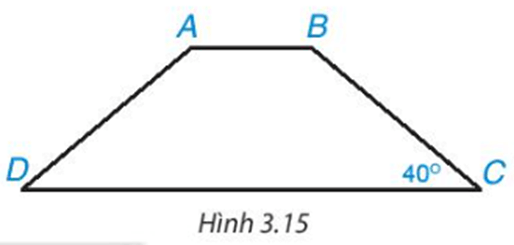
Luyện tập 1 trang 53 Toán 8 Tập 1: Tính các góc của hình thang cân ABCD (AB // CD), biết $\hat{C}=40°$ (H.3.15).

Lời giải:

Hình thang cân ABCD (AB // CD) nên ta có:

• $\hat{A}=\hat{B};\hat{D}=\hat{C}=40°$ ;

• $\hat{A}+\hat{B}+\hat{C}+\hat{D}=360°$ .

Khi đó: $\hat{A}+\hat{A}+40°+40°=360°$

Hay $2\hat{A}+80°=360°$

Suy ra $2\hat{A}=360°-80°=280°$ .

Do đó $\hat{A}=140°$ nên $\hat{B}=140°$ .

Vậy $\hat{A}=140°$ ; $\hat{B}=140°$ ; $\hat{C}=40°;\hat{D}=40°$ .

Lời giải bài tập Toán 8 Bài 11: Hình thang cân hay, chi tiết khác:

HĐ1 trang 53 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 11: Hình thang cân - Kết nối tri thức

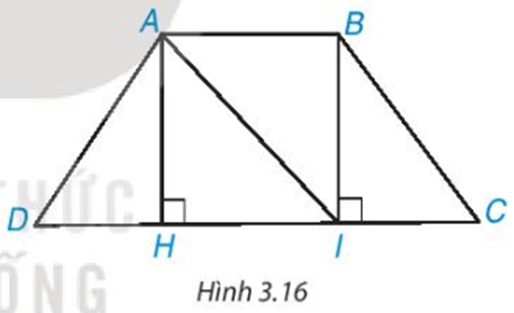
HĐ1 trang 53 Toán 8 Tập 1: Cho hình thang cân ABCD, AB // CD và AB < CD (H.3.16).

a) Từ A và B kẻ AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD. Chứng minh rằng AH = BI bằng cách chứng minh ∆AHI = ∆IBA.

b) Chứng minh ∆AHD = ∆BIC, từ đó suy ra AD = BC.

Lời giải:

a) Vì ABCD là hình thang cân (AB // CD) nên $\widehat{BAI}=\widehat{AIH}$ (hai góc so le trong).

Ta có AH ⊥ DC, BI ⊥ DC suy ra AH // BI.

Do đó $\widehat{AIB}=\widehat{HAI}$ (hai góc so le trong).

Xét ∆AHI và ∆IBA có:

$\widehat{BAI}=\widehat{AIH}$ (chứng minh trên);

Cạnh AI chung;

$\widehat{AIB}=\widehat{HAI}$ (hai góc so le trong).

Do đó ∆AHI = ∆IBA (c.g.c).

Suy ra AH = BI (hai cạnh tương ứng).

b) Vì ABCD là hình thang cân (AB // CD) nên $\hat{C}=\hat{D}$ (1)

Xét ∆AHD vuông tại H có $\widehat{DAH}+\hat{D}=90°$ (2) (trong tam giác vuông, hai góc nhọn có tổng số đo bằng 90°).

Tương tự, ∆BIC vuông tại I có $\widehat{CBI}+\hat{C}=90°$ (3)

Từ (1), (2) và (3) suy ra $\widehat{DAH}=\widehat{CBI}$ .

Xét ∆AHD và ∆BIC có:

$\widehat{AHD}=\widehat{BIC}=90°$ (vì AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD);

AH = BI (chứng minh câu a);

$\widehat{DAH}=\widehat{CBI}$ (chứng minh trên).

Do đó ∆AHD = ∆BIC (cạnh góc vuông – góc nhọn kề).

Suy ra AD = BC (hai cạnh tương ứng).

Lời giải bài tập Toán 8 Bài 11: Hình thang cân hay, chi tiết khác:

Luyện tập 2 trang 53 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 11: Hình thang cân - Kết nối tri thức

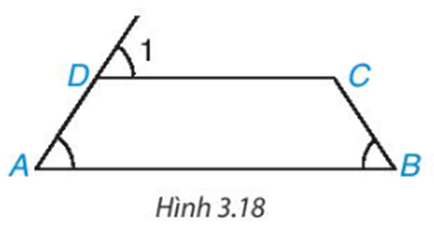
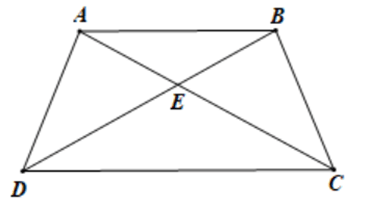
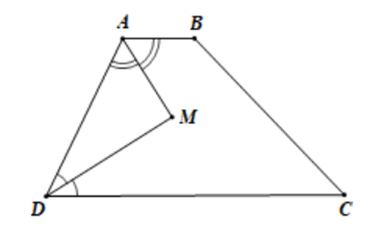
Luyện tập 2 trang 53 Toán 8 Tập 1: Cho tứ giác ABCD như Hình 3.18. Biết rằng $\hat{A}=\hat{B}={\hat{D}}_1$ . Chứng minh rằng AD = BC.

Lời giải:

Ta có $\hat{A}={\hat{D}}_1$ mà hai góc này ở vị trí đồng vị nên AB // CD.

Suy ra tứ giác ABCD là hình thang.

Mặt khác hình thang ABCD có $\hat{A}=\hat{B}$ nên ABCD là hình thang cân.

Do đó AD = BC (đpcm).

Lời giải bài tập Toán 8 Bài 11: Hình thang cân hay, chi tiết khác:

HĐ2 trang 54 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 11: Hình thang cân - Kết nối tri thức

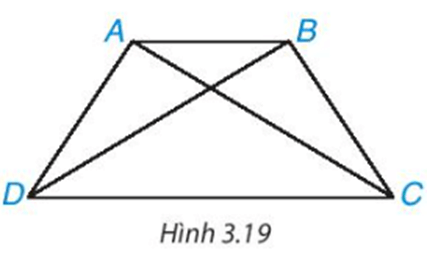
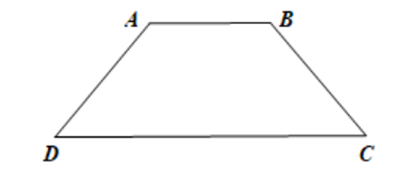
HĐ2 trang 54 Toán 8 Tập 1: Cho hình thang cân ABCD, kẻ hai đường chéo AC, BD (H.3.19). Hãy chứng minh ∆ACD = ∆BDC. Từ đó suy ra AC = BD.

Lời giải:

Vì ABCD là hình thang cân (AB // CD) nên AD = BC; $\widehat{ADC}=\widehat{BCD}$ .

Xét ∆ACD và ∆BDC có

AD = BC (chứng minh trên);

$\widehat{ADC}=\widehat{BCD}$ (chứng minh trên);

Cạnh CD chung.

Do đó ∆ACD = ∆BDC (c.g.c).

Suy ra AC = BD (hai góc tương ứng).

Lời giải bài tập Toán 8 Bài 11: Hình thang cân hay, chi tiết khác:

Luyện tập 3 trang 54 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 11: Hình thang cân - Kết nối tri thức

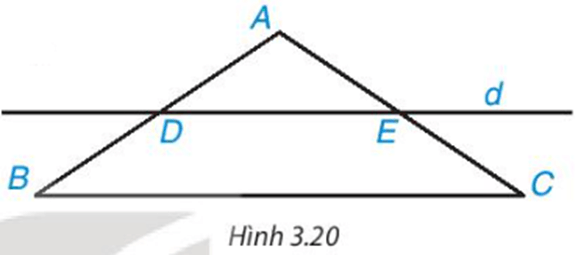
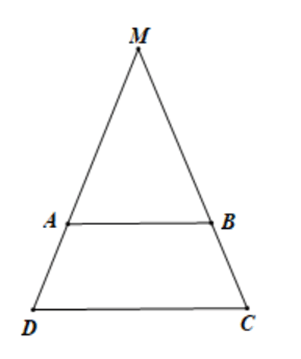
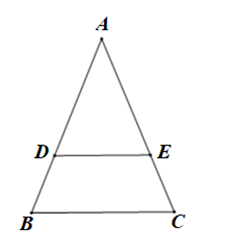
Luyện tập 3 trang 54 Toán 8 Tập 1: Cho tam giác ABC cân tại A. Kẻ một đường thẳng d song song với BC, d cắt cạnh AB tại D và cắt cạnh AC tại E (H.3.20).

a) Tứ giác DECB là hình gì?

b) Chứng minh BE = CD.

Lời giải:

a) Theo đề bài: d // BC nên DE // BC

Suy ra DECB là hình thang.

Vì tam giác ABC cân tại A nên $\hat{B}=\hat{C}$ .

Hình thang DECB có $\hat{B}=\hat{C}$ nên là hình thang cân.

b) Hình thang cân DECB có BE và CD là hai đường chéo.

Do đó BE = CD (đpcm).

Lời giải bài tập Toán 8 Bài 11: Hình thang cân hay, chi tiết khác:

Thực hành trang 55 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 11: Hình thang cân - Kết nối tri thức

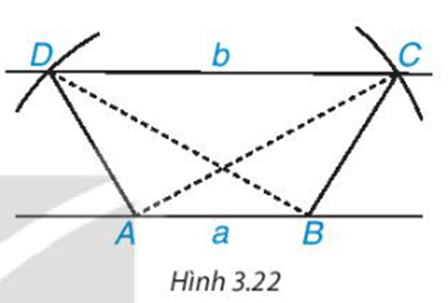
Thực hành trang 55 Toán 8 Tập 1: (H.3.22)

a) Vẽ hình thang có hai đường chéo bằng nhau theo các bước sau:

- Vẽ hai đường thẳng song song a, b. Trên a lấy hai điểm A, B.

- Vẽ hai cung tròn tâm A và B có cùng bán kính sao cho cung tròn tâm A cắt b tại C; cung tròn tâm B cắt b tại D và hai đoạn thẳng AC, BD cắt nhau. Hình thang ABCD có hai đường chéo AC và BD bằng nhau.

b) Hình thang ABCD có là hình thang cân không? Vì sao?

Lời giải:

a) Học sinh vẽ hình theo các bước đã nêu ở đề bài.

b) Hình thang ABCD có hai đường chéo AC = BD.

Do đó ABCD là hình thang cân.

Lời giải bài tập Toán 8 Bài 11: Hình thang cân hay, chi tiết khác:

Vận dụng trang 55 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 11: Hình thang cân - Kết nối tri thức

Vận dụng trang 55 Toán 8 Tập 1: Hãy giải bài toán mở đầu.

Cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy thì được hai hình thang. Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu (Hình 3.11). Hãy giải thích tại sao hình tạo thành cũng là một hình thang cân.

Lời giải:

Ta cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy.

Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu nên $\widehat{AMN}=\widehat{M^{\text{'}}}$ (1)

Tứ giác ABCD là hình thang cân có AB // CD

Mà theo cách ghép thì chỗ ghép ở các đỉnh M, B tạo thành đường thẳng AN’, chỗ ghép ở các đỉnh N, C tạo thành đường thẳng DM’. Do đó AN’ // M’D.

Suy ra $\widehat{AMN}=\widehat{MN{M}^{\text{'}}}$ (so le trong) (2)

Từ (1) và (2) suy ra $\widehat{MN{M}^{\text{'}}}=\widehat{M^{\text{'}}}$.

Xét tứ giác MN’M’N có MN’ // M’N nên là hình thang.

Lại có $\widehat{MN{M}^{\text{'}}}=\widehat{M^{\text{'}}}$ nên MN’M’N là hình thang cân.

Lời giải bài tập Toán 8 Bài 11: Hình thang cân hay, chi tiết khác:

Bài 3.4 trang 55 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 11: Hình thang cân - Kết nối tri thức

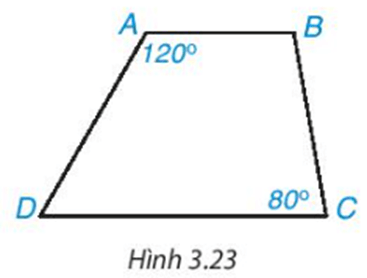
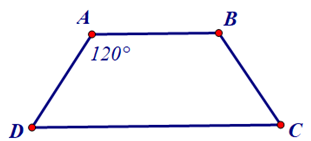
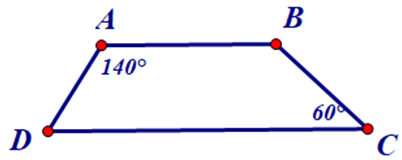
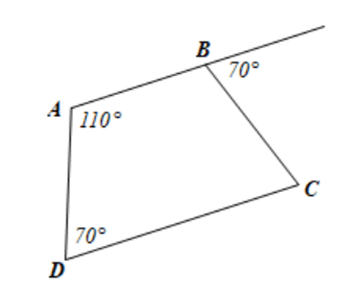
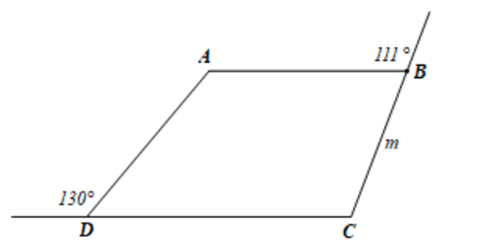
Bài 3.4 trang 55 Toán 8 Tập 1: Hình thang trong Hình 3.23 có là hình thang cân không? Vì sao?

Lời giải:

Cách 1:

Do ABCD là hình thang có AB // CD nên ta có: $\hat{A}+\hat{D}=180°$

Suy ra $\hat{D}=180°-\hat{A}=180°-120°=60°$

Hình thang ABCD có $\hat{D}\ne \hat{C}$ (do 60° ≠ 80°) nên không phải là hình thang cân.

Cách 2:

Giả sử hình thang ABCD là hình thang cân. Khi đó $\hat{A}=\hat{B}=120°;\hat{C}=\hat{D}=80°$ .

Suy ra $\hat{A}+\hat{B}+\hat{C}+\hat{D}=120°+120°+80°+80°=400°>360°$ (không thỏa mãn định lí tổng bốn góc trong một tứ giác).

Khi đó, ABCD không phải là tứ giác, điều này mâu thuẫn với giả thiết ABCD là hình thang cân (hình thang cân cũng là tứ giác).

Do đó ABCD không phải là hình thang cân.

Lời giải bài tập Toán 8 Bài 11: Hình thang cân hay, chi tiết khác:

Bài 3.5 trang 55 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 11: Hình thang cân - Kết nối tri thức

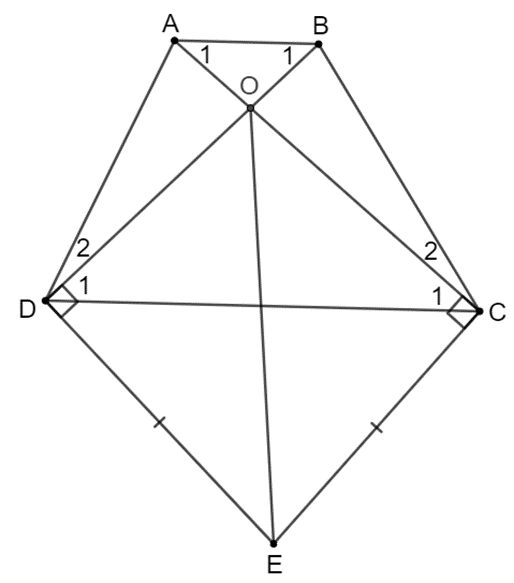
Bài 3.5 trang 55 Toán 8 Tập 1: Cho hình thang ABCD (AB // CD). Kẻ đường thẳng vuông góc với AC tại C và đường thẳng vuông góc với BD tại D, hai đường thẳng này cắt nhau tại E. Chứng minh rằng nếu EC = ED thì hình thang ABCD là hình thang cân.

Lời giải:

Gọi O là giao điểm của AC và BD.

Xét ∆DOE và ∆COE có:

$\widehat{ODE}=\widehat{OCE}=90°$ (vì OD ⊥ DE; OC ⊥ CE);

EC = ED (giả thiết);

Cạnh OE chung

Do đó ∆DOE = ∆COE (cạnh huyền – cạnh góc vuông).

Suy ra OC = OD (hai cạnh tương ứng) (1)

Do đó tam giác OCD cân tại O nên ${\hat{C}}_1={\hat{D}}_1$ .

Vì ABCD là hình thang nên AB // CD suy ra ${\hat{A}}_1={\hat{C}}_1;{\hat{B}}_1={\hat{D}}_1$ (cặp góc so le trong).

Do đó ${\hat{A}}_1={\hat{B}}_1$ (vì ${\hat{C}}_1={\hat{D}}_1$ ).

Suy ra tam giác OAB cân tại O nên OA = OB (2)

Ta có: AC = OA + OC và BD = OB + OD (3)

Từ (1), (2) và (3) suy ra AC = BD

Hình thang ABCD có AC = BD nên ABCD là hình thang cân.

Lời giải bài tập Toán 8 Bài 11: Hình thang cân hay, chi tiết khác:

Bài 3.6 trang 55 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 11: Hình thang cân - Kết nối tri thức

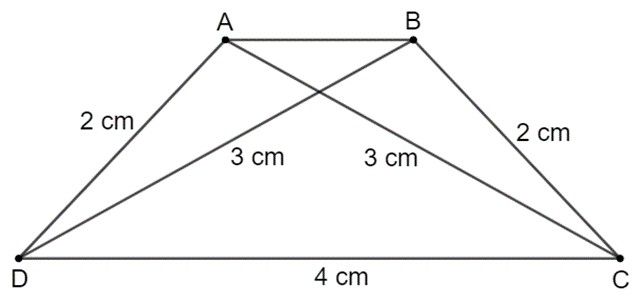
Bài 3.6 trang 55 Toán 8 Tập 1: Vẽ hình thang cân ABCD (AB // CD) biết đáy lớn CD dài 4 cm, cạnh bên dài 2 cm và đường chéo dài 3 cm.

Lời giải:

Cách vẽ hình thang cân ABCD có đáy lớn CD dài 4 cm, cạnh bên dài 2 cm và đường chéo dài 3 cm:

– Vẽ cạnh CD = 4 cm.

– Dùng compa vẽ hai đường tròn (D; 2 cm) và (C; 3 cm). Hai đường tròn này cắt nhau tại điểm A.

– Dùng compa vẽ hai đường tròn (D; 3 cm) và (C; 2 cm). Hai đường tròn này cắt nhau tại điểm B.

– Nối AB, AD, BC ta được hình thang cân ABCD (như hình vẽ).

Lời giải bài tập Toán 8 Bài 11: Hình thang cân hay, chi tiết khác:

Bài 3.7 trang 55 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 11: Hình thang cân - Kết nối tri thức

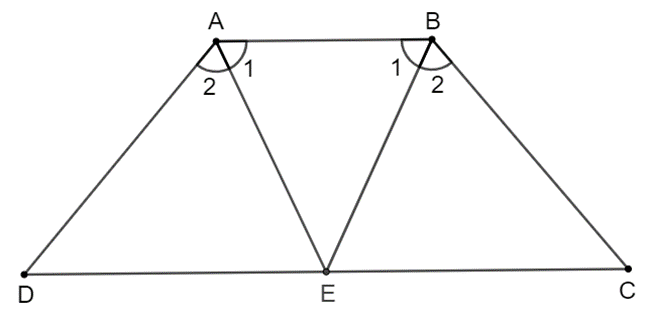
Bài 3.7 trang 55 Toán 8 Tập 1: Hai tia phân giác của hai góc A, B của hình thang cân ABCD (AB // CD) cắt nhau tại điểm E trên cạnh đáy CD. Chứng minh rằng EC = ED.

Lời giải:

Vì ABCD là hình thang cân nên $\widehat{DAB}=\widehat{ABC};\hat{C}=\hat{D};AD=BC$ .

Theo đề bài, ta có AE, BE lần lượt là tia phân giác của $\widehat{BAD}$ và $\widehat{ABC}$ .

Suy ra ${\hat{A}}_1={\hat{A}}_2=\frac{1}{2}\widehat{DAB};{\hat{B}}_1={\hat{B}}_2=\frac{1}{2}\widehat{ABC}$ .

Mà $\widehat{DAB}=\widehat{ABC}$ nên ${\hat{A}}_1={\hat{A}}_2={\hat{B}}_1={\hat{B}}_2$ .

Xét tam giác EAB cân tại E (vì ${\hat{A}}_1={\hat{B}}_1$ ) nên EA = EB.

Xét ∆ADE và ∆BCE có:

EA = EB (chứng minh trên);

${\hat{A}}_2={\hat{B}}_2$ (chứng minh trên);

AD = BC (chứng minh trên)

Do đó ∆ADE = ∆BCE (c.g.c).

Suy ra EC = ED (hai cạnh tương ứng).

Lời giải bài tập Toán 8 Bài 11: Hình thang cân hay, chi tiết khác:

Bài 3.8 trang 55 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 11: Hình thang cân - Kết nối tri thức

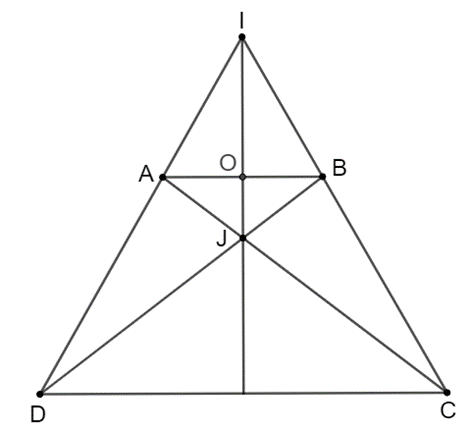
Bài 3.8 trang 55 Toán 8 Tập 1: Hình thang cân ABCD (AB // CD, AB < CD) có các đường thẳng AD, BC cắt nhau tại I, các đường thẳng AC, BD cắt nhau tại J. Chứng minh rằng đường thẳng IJ là đường trung trực của đoạn thẳng AB.

Lời giải:

•Vì ABCD là hình thang cân nên $\widehat{BAD}=\widehat{ABC};\widehat{ADC}=\widehat{BCD}$; AD = BC; AC = BD.

Xét DICD cân tại I (vì $\widehat{ADC}=\widehat{BCD}$) nên IC = ID.

Suy ra IC – BC = ID – AD, hay IB = IA

Do đó I cách đều A và B nên I nằm trên đường trung trực của AB (1)

•Xét ∆ABD và ∆BAC có:

AB là cạnh chung;

$\widehat{BAD}=\widehat{ABC}$ (chứng minh trên);

AD = BC (chứng minh trên).

Do đó ∆ABD = ∆BAC (c.g.c)

Suy ra $\widehat{ABD}=\widehat{BAC}$ (hai góc tương ứng).

Tam giác JAB cân tại J (vì $\widehat{ABD}=\widehat{BAC}$ ) nên JA = JB

Do đó J cách đều A và B nên J nằm trên đường trung trực của AB (2)

Từ (1) và (2) suy ra I, J cùng nằm trên đường thẳng IJ là đường trung trực của đoạn thẳng AB.

Lời giải bài tập Toán 8 Bài 11: Hình thang cân hay, chi tiết khác:

SBT Toán 8 Kết nối tri thức Bài 11: Hình thang cân

Với giải sách bài tập Toán 8 Bài 11: Hình thang cân sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 8 dễ dàng làm bài tập trong SBT Toán 8 Bài 11.

Giải SBT Toán 8 Kết nối tri thức Bài 11: Hình thang cân

Vở thực hành Toán 8 Bài 11: Hình thang cân - Kết nối tri thức

Với giải vở thực hành Toán 8 Bài 11: Hình thang cân sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 8 dễ dàng làm bài tập về nhà trong VTH Toán 8 Bài 11.

Giải vở thực hành Toán 8 Bài 11: Hình thang cân - Kết nối tri thức

B – CÂU HỎI TRẮC NGHIỆM

Chọn phương án đúng trong mỗi câu sau:

Hình thang cân (Lý thuyết Toán lớp 8) | Kết nối tri thức

Với tóm tắt lý thuyết Toán 8 Bài 11: Hình thang cân sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 8 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Hình thang cân (Lý thuyết Toán lớp 8) | Kết nối tri thức

Lý thuyết Hình thang cân

1. Hình thang. Hình thang cân

+ Hình thang là tứ giác có hai cạnh đối song song.

+ Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

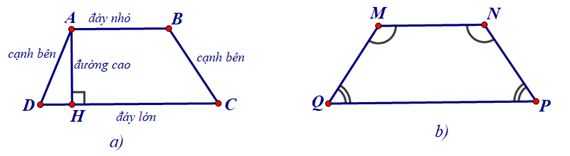
Xét các hình dưới đây:

+ Hình a là hình thang ABCD (AB // CD). Hai cạnh song song gọi là hai đáy, hai cạnh còn lại gọi là hai cạnh bên, đường vuông góc AH kẻ từ A đến CD gọi là một đường cao của hình thang ABCD.

+ Hình b là hình thang cân MNPQ  (MN // PQ)

Hai góc M, N kề đáy nhỏ MN, $\hat{M}=\hat{N}$

Hai góc C, D kề đáy lớn CD, $\hat{C}=\hat{D}$ .

Chú ý: Trong hình thang, hai góc kề một đáy bằng nhau thì hai góc kề đáy kia cũng bằng nhau.

Ví dụ 1: Tính các góc của hình thang cân ABCD (AB // CD) biết $\hat{A}=120°$.

Vì ABCD (AB // CD) là hình thang cân nên $\hat{B}=\hat{A}=120°.$

Do $\hat{A}+\hat{D}=180°$  (hai góc kề bù) nên $\hat{D}=180°-\hat{A}=180°-120°=60°$ .

$\Rightarrow \hat{C}=\hat{D}=60°$.

2. Tính chất của hình thang cân

+ Định lí 1: Trong hình thang cân, hai cạnh bên bằng nhau.

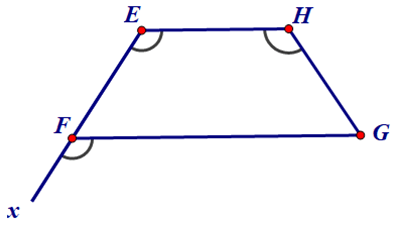
Ví dụ 2: Cho tứ giác EFGH như hình dưới, biết  $\hat{E}=\hat{H}=\widehat{xFG}.$

Chứng minh EF = HG.

Hướng dẫn giải

Ta có: $\hat{E}=\widehat{xFG}$  mà hai góc này ở vị trí đồng vị nên EH // FG suy ra EFGH là hình thang.

Hình thang EFGH có $\hat{E}=\hat{H}$  (hai góc kề đáy EH bằng nhau) nên EFGH là hình thang cân

EF = GH (hai cạnh bên bằng nhau).

+ Định lí 2: Trong hình thang cân, hai đường chéo bằng nhau.

Ví dụ 3: (Chứng minh Định Lí 2) Cho hình thang cân MNEF (MN // EF), chứng minh ME = NF.

Hướng dẫn giải

Vì MNEF (MN // EF) là hình thang cân nên $\widehat{FMN}=\widehat{MNE}$  và MF = NE.

Xét $\Delta MNF$ và $\Delta NME$  có:

MF = NE

$\widehat{FMN}=\widehat{MNE}$

MN chung

Do đó $\Delta MNF=\Delta NME$  (cạnh - góc - cạnh)

Suy ra ME = NF (cạnh tương ứng bằng nhau).

3. Dấu hiệu nhận biết

+ Định lí 3 (Dấu hiệu nhận biết hình thang cân): Nếu một hình thang có hai đường chéo bằng nhau thì đó là hình thang cân.

Chú ý: Định lí 3 là định lí đảo của định lí 2. Giả thiết của định lí này là kết luận của định lí kia.

Bài tập Hình thang cân

Bài 1. Hình thang ABCD (AB // CD) trong hình bên dưới có phải hình thang cân không? Vì sao?

Hướng dẫn giải

Giả sử ABCD (AB // CD) là hình thang cân.

Khi đó, ta có: $\hat{A}=\hat{B}=140°,\hat{C}=\hat{D}=60°$.

Tổng 4 góc trong hình thang ABCD là $\hat{A}+\hat{B}+\hat{C}+\hat{D}=400°>360°$ .

Suy ra ABCD không phải là hình thang cân.

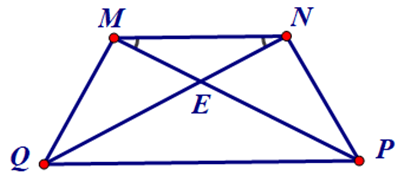
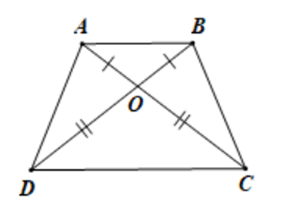
Bài 2. Cho hình thang MNPQ (MN // PQ) có $\widehat{NMP}=\widehat{MNQ},$  E là giao điểm của MP và NQ. Chứng minh hình thang MNPQ là hình thang cân.

Hướng dẫn giải

Vì MN // QP nên $\widehat{NMP}=\widehat{MPQ}$  và $\widehat{NQP}=\widehat{MNQ}$(các cặp góc so le trong)

Mà $\widehat{NMP}=\widehat{MNQ}\Rightarrow \widehat{NMP}=\widehat{MPQ}=\widehat{NQP}=\widehat{MNQ}$.

$\Delta MNE$ có $\widehat{NMP}=\widehat{MNQ}$ nên $\Delta MNE$cân tại E

Suy ra ME = NE (1)

$\Delta QEP$ có $\widehat{MPQ}=\widehat{NQP}$  nên $\Delta QEP$  cân tại E

Suy ra EQ = EP (2)

Từ (1) và (2) ta có: ME + EP = NE +  EQ hay MP = NQ

Suy ra MNPQ là hình thang cân (dấu hiệu nhận biết).

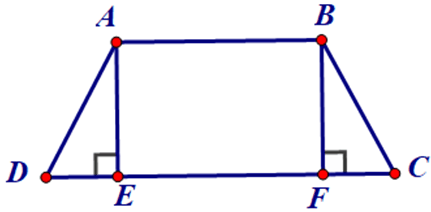
Bài 3. Cho hình thang cân ABCD (AB // CD) có các đường cao AE, BF. Chứng minh DE = CF.

Hướng dẫn giải

Vì ABCD (AB // CD) là hình thang cân nên $\hat{D}=\hat{C}$ và AD = BC.

Xét $\Delta AED$  và $\Delta BFC$  có: 

$\widehat{AED}=\widehat{BFC}=90°(AE\perp DC,BF\perp DC)$

$\hat{D}=\hat{C}$(chứng minh trên)

AD = BC (chứng minh trên)

Do đó $\Delta AED=\Delta BFC$  (cạnh huyền - góc nhọn)

Suy ra DE = CF (cạnh tương ứng bằng nhau).

Học tốt Hình thang cân

Các bài học để học tốt Hình thang cân Toán lớp 8 hay khác:

15 Bài tập Hình thang cân (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 8

Với 15 bài tập trắc nghiệm Hình thang cân Toán lớp 8 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 8.

15 Bài tập Hình thang cân (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 8

Câu 1. Trong các khẳng định sau, khẳng định nào sai?

A. Tứ giác có hai cạnh bên bằng nhau là hình thang cân.

B. Hình thang cân có hai cạnh bên bằng nhau.

C. Hình thang cân có hai góc đối bù nhau.

D. Hình thang cân có hai góc kề một cạnh đáy bằng nhau.

Câu 2. Hình thang cân là hình thang có

A. hai góc kề bằng nhau.

B. hai góc đối bằng nhau.

C. hai cạnh đối bằng nhau.

D. hai đường chéo bằng nhau.

Câu 3. Tứ giác ABCD có AB // CD là một hình thang, ta gọi

A. các đoạn thẳng AB và CD là các cạnh bên.

B. các đoạn thẳng AB và CD là các cạnh đáy.

C. các đoạn thẳng AB và CD là các đường chéo.

D. các đoạn thẳng AB và CD là các đường cao.

Câu 4. Cho hình vẽ, số đo $\widehat{\text{BCD}}$ bằng:

A. 70°

B. 110°

C. 80°

D. 140°

Câu 5. Cho hình thang cân ABCD có AB // CD và AC = 12 cm, AB = 6 cm. Độ dài BD là

A. 12 cm

B. 13 cm

C. 7 cm

D. 6 cm

Câu 6. Cho hình thang cân ABCD có AB // CD. Gọi M là giao điểm của AC và BC. Tam giác MCD là tam giác gì?

A. Tam giác cân

B. Tam giác nhọn

C. Tam giác vuông

D. Tam giác tù

Câu 7. Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD. Tìm khẳng định sai trong các khẳng định sau:

A. ABCD là hình thang cân

B. AC = BD

C. BC = AD

D. Tam giác AOD cân tại C.

Câu 8. Hình thang cân có một góc bằng 50°. Hiệu giữa hai góc kề một cạnh bên là:

A. 130°

B. 100°

C. 80°

D. 50°

Câu 9. Cho hình thang ABCD (AB // CD) biết $\hat{A}\text{= 58}°$ thì:

A. $\hat{D}\text{= 122}°$

B. $\hat{D}\text{= 212}°$

C. $\hat{D}\text{= 22}°$

D. $\hat{D}\text{= 0}°$

Câu 10. Trong hình thang có hai góc tù:

A. hai góc còn lại cũng là góc tù.

B. hai góc còn lại là hai góc vuông.

C. hai góc còn lại gòm một góc tù và một góc nhọn

D. hai góc còn lại là hai góc nhọn.

Câu 11. Cho hình thang cân ABCD (AB // CD). Tìm khẳng định sai trong các khẳng định sau:

A. $\text{ΔABC = ΔBAD}$

B. $\widehat{\text{CBA}}\text{=}\widehat{\text{DBA}}$

C. $\text{ΔABE}$ cân

D. $\text{ΔAED}$ cân

Câu 12. Cho tam giác ABC cân tại A. các điểm D và E lần lượt trên các cạnh AB, AC sao cho DE // BC. Tìm khẳng định đúng:

A. BE = DC

B. BE = DE

C. DC = DE

D. DC = BC

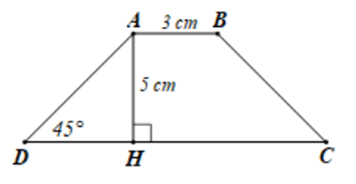
Câu 13. Cho hình thang cân ABCD (AB // CD) đáy nhỏ AB = 3 cm, đường cao AH = 5 cm. Biết $\hat{D}=45°$. Độ dài đáy lớn CD là:

A. 8cm

B. 11 cm

C. 12 cm

D. 13 cm

Câu 14. Cho hình vẽ sau, tính các góc A, C của hình thang ABCD (AB // CD) biết:

A. $\hat{A}=\hat{C}=111°$

B. $\hat{A}=\hat{C}=130°$

C. $\hat{A}=111°;\hat{C}=130°$

D. $\hat{A}=130°;\hat{C}=111°$

Câu 15. Hình thang ABCD (AB // CD) có các tia phân giác của $\hat{A};\hat{D}$ cắt nhau tại M thì

A. $\widehat{\text{AMD}}\text{= 180}°$

B. $\widehat{\text{AMD}}\text{= 150}°$

C. $\widehat{\text{AMD}}\text{= 90}°$

D. $\widehat{\text{AMD}}\text{= 60}°$

Xem thêm bài tập trắc nghiệm Toán lớp 8 Kết nối tri thức có đáp án hay khác: