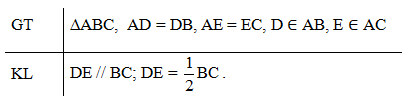Giải Toán 8 | No tags
Với giải bài tập Toán 8 Bài 16: Đường trung bình của tam giác sách Kết nối tri thức hay nhất, chi tiết giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 Bài 16.
Video Giải Toán 8 Bài 16: Đường trung bình của tam giác - Cô Vũ Chuyên (Giáo viên VietJack)
Mở đầu trang 81 Toán 8 Tập 1: Cho B và C là hai điểm cách nhau bởi một hồ nước như Hình 4.12 với D, E lần lượt là trung điểm của AB và AC. Biết DE = 500 m, liệu không cần đo trực tiếp, ta có thể tính được khoảng cách giữa hai điểm B và C không?
Lời giải:
Sau bài học này ta giải quyết được bài toán như sau:
Trong tam giác ABC có D, E lần lượt là trung điểm của AB và AC nên D ∈ AB; E ∈ AC và AD = BD; AE = EC.
Suy ra DE là đường trung bình của tam giác ABC.
Do đó suy ra BC = 2DE = 2 . 500 = 1 000 (m)
Vậy khoảng cách giữa hai điểm B và C bằng 1 000 m.
Lời giải bài tập Toán 8 Bài 16: Đường trung bình của tam giác hay, chi tiết khác:
Câu hỏi trang 81 Toán 8 Tập 1: Em hãy chỉ ra các đường trung bình của ∆DEF và ∆IHK trong Hình 4.14.
Lời giải:
Quan sát Hình 4.14, ta thấy:
* Xét ∆DEF có M là trung điểm của cạnh DE; N là trung điểm của cạnh DF nên MN là đường trung bình của ∆DEF.
* Xét ∆IHK có:
• B là trung điểm của cạnh IH; C là trung điểm của cạnh IK nên BC là đường trung bình của ∆IHK.
• B là trung điểm của cạnh IH; A là trung điểm của cạnh HK nên AB là đường trung bình của ∆IHK.
• A là trung điểm của cạnh HK; C là trung điểm của cạnh IK nên AC là đường trung bình của ∆IHK.
Vậy đường trung bình của ∆DEF là MN; các đường trung bình của ∆IHK là AB, BC, AC.
Lời giải bài tập Toán 8 Bài 16: Đường trung bình của tam giác hay, chi tiết khác:
HĐ1 trang 82 Toán 8 Tập 1: Cho DE là đường trung bình của tam giác ABC (H.4.15).
Sử dụng định lí Thalès đảo, chứng minh rằng DE // BC.
Lời giải:
Ta có DE là đường trung bình của tam giác ABC nên:
• D là trung điểm của AB hay AD = AB nên ;
• E là trung điểm của AC hay AE = AC nên .
Xét tam giác ABC có , theo định lí Thalès đảo, ta suy ra DE // BC (đpcm).
Lời giải bài tập Toán 8 Bài 16: Đường trung bình của tam giác hay, chi tiết khác:
HĐ2 trang 82 Toán 8 Tập 1: Cho DE là đường trung bình của tam giác ABC (H.4.15).
Lời giải:
Ta có: F là trung điểm của BC nên CF = BC, suy ra .
Mà E là trung điểm của AC nên CE = CA, suy ra .
Do đó trong DABC có , theo định lí Thalès đảo ta có: EF // AB.
Xét tứ giác DEFB có DE // BF (vì DE // BC, theo HĐ1); EF // BD (vì EF // AB)
Do đó tứ giác DEFB là hình bình hành.
Suy ra DE = BF mà BF = BC nên DE = BC.
Lời giải bài tập Toán 8 Bài 16: Đường trung bình của tam giác hay, chi tiết khác:
Luyện tập trang 83 Toán 8 Tập 1: Cho tam giác ABC cân tại A, D và E lần lượt là trung điểm của AB, AC. Tứ giác DECB là hình gì? Tại sao?
Lời giải:
Tam giác ABC cân tại A nên .
Vì D và E lần lượt là trung điểm của AB, AC nên DE là đường trung bình của tam giác ABC.
Suy ra DE // BC nên tứ giác DECB là hình thang.
Hình thang DECB có nên là hình thang cân.
Lời giải bài tập Toán 8 Bài 16: Đường trung bình của tam giác hay, chi tiết khác:
Vận dụng trang 83 Toán 8 Tập 1: Em hãy trả lời câu hỏi trong tình huống mở đầu.
Cho B và C là hai điểm cách nhau bởi một hồ nước như Hình 4.12 với D, E lần lượt là trung điểm của AB và AC. Biết DE = 500 m, liệu không cần đo trực tiếp, ta có thể tính được khoảng cách giữa hai điểm B và C không?
Lời giải:
Trong tam giác ABC có D, E lần lượt là trung điểm của AB và AC nên D ∈ AB; E ∈ AC và AD = BD; AE = EC.
Suy ra DE là đường trung bình của tam giác ABC.
Do đó suy ra BC = 2DE = 2 . 500 = 1 000 (m)
Lời giải bài tập Toán 8 Bài 16: Đường trung bình của tam giác hay, chi tiết khác:
Bài 4.6 trang 83 Toán 8 Tập 1: Tính các độ dài x, y trong Hình 4.18.
Lời giải:
• Hình 4.18a)
Ta có: DH = HF, H ∈ DF nên H là trung điểm của DF;
EK = KF, K ∈ EF nên K là trung điểm của EF.
Xét tam giác DEF có H, K lần lượt là trung điểm của DF, EF nên HK là đường trung bình của tam giác DEF.
Suy ra .
Do đó x = 2HK = 2 . 3 = 6.
• Hình 4.18b)
Vì MN ⊥ AB, AC ⊥ AB nên MN // AC.
Mà M là trung điểm của AB (vì AM = BM = 3)
Suy ra MN là đường trung bình của tam giác ABC.
Do đó N là trung điểm của BC nên y = NC = BN = 5.
Vậy x = 6; y = 5.
Lời giải bài tập Toán 8 Bài 16: Đường trung bình của tam giác hay, chi tiết khác:
Bài 4.7 trang 83 Toán 8 Tập 1: Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC.
a) Chứng minh tứ giác BMNC là hình thang.
b) Tứ giác MNPB là hình gì? Tại sao?
Lời giải:
a) Vì M, N lần lượt là trung điểm của các cạnh AB, AC nên MN là đường trung bình của tam giác ABC suy ra MN // BC.
Tứ giác BMNC có MN // BC nên tứ giác BMNC là hình thang (đpcm).
b) Vì N, P lần lượt là trung điểm của các cạnh AC, BC nên NP là đường trung bình của tam giác ABC suy ra NP // AB hay NP // MB.
Tứ giác MNPB có MN // BP (do MN // BC); BM // NP (chứng minh trên).
Do đó, tứ giác MNPB là hình bình hành.
Lời giải bài tập Toán 8 Bài 16: Đường trung bình của tam giác hay, chi tiết khác:
Bài 4.8 trang 83 Toán 8 Tập 1: Cho tam giác ABC có trung tuyến AM. Lấy điểm D và E trên cạnh AB sao cho AD = DE = EB và D nằm giữa hai điểm A, E.
a) Chứng minh DC // EM.
b) DC cắt AM tại I. Chứng minh I là trung điểm của AM.
Lời giải:
a) Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của BC.
Ta có BE = DE và E ∈ BD nên E là trung điểm của BD.
Xét tam giác BCD có E, M lần lượt là trung điểm của BD, BC nên EM là đường trung bình của tam giác BCD.
Do đó DC // EM (tính chất đường trung bình).
b) Ta có D là trung điểm của AE (vì AD = DE, D ∈ AE).
Mà DI // EM (vì DC // EM).
Do đó DI là đường trung bình của tam giác AEM.
Suy ra I là trung điểm của AM.
Lời giải bài tập Toán 8 Bài 16: Đường trung bình của tam giác hay, chi tiết khác:
Bài 4.9 trang 83 Toán 8 Tập 1: Cho hình chữ nhật ABCD có AC cắt BD tại O. Gọi H, K lần lượt là trung điểm của AB, AD. Chứng minh tứ giác AHOK là hình chữ nhật.
Lời giải:
Vì ABCD là hình chữ nhật nên và hai đường chéo AC, BD bằng nhau và cắt nhau tại trung điểm O của mỗi đường.
Suy ra AB ⊥ AD; O là trung điểm của AC và BD.
Vì O, H lần lượt là trung điểm của BD và AB nên OH là đường trung bình của tam giác ABD.
Suy ra OH // AD mà AB ⊥ AD nên OH ⊥ AB hay .
Tương tự, ta chứng minh được: OK ⊥ AD hay .
Ta có:
Suy ra .
Tứ giác AHOK có .
Do đó, tứ giác AHOK là hình chữ nhật.
Lời giải bài tập Toán 8 Bài 16: Đường trung bình của tam giác hay, chi tiết khác:
Với giải sách bài tập Toán 8 Bài 16: Đường trung bình của tam giác sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 8 dễ dàng làm bài tập trong SBT Toán 8 Bài 16.
Với giải vở thực hành Toán 8 Bài 16: Đường trung bình của tam giác sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 8 dễ dàng làm bài tập về nhà trong VTH Toán 8 Bài 16.
B – CÂU HỎI TRẮC NGHIỆM
Chọn phương án đúng trong mỗi câu sau:
Với tóm tắt lý thuyết Toán 8 Bài 16: Đường trung bình của tam giác sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 8 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.
1. Định nghĩa đường trung bình của tam giác
Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
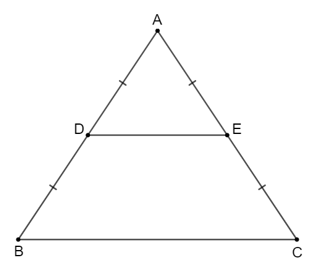
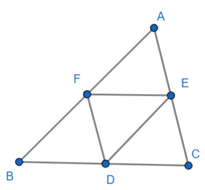
Ví dụ: Chỉ ra các đường trung bình trong tam giác sau với D, E, F lần lượt là trung điểm của BC, AC, AB.
Hướng dẫn giải
Các đường trung bình của ∆ABC là DE, DF, EF.
2. Tính chất đường trung bình của tam giác
2.1. Tính chất đường trung bình của tam giác
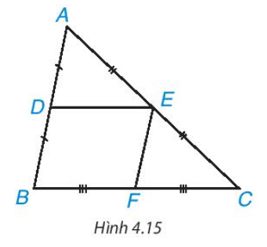
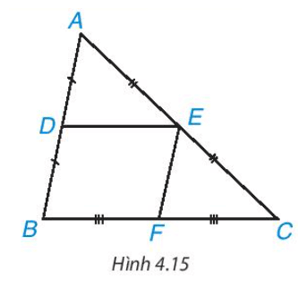
Định lí: Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh đó.
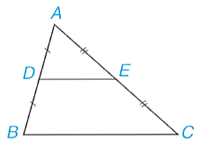
2.2. Chứng minh định lí
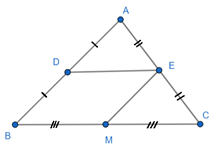
Gọi M là trung điểm của BC.
Tam giác ABC có , suy ra DE // BC (định lí Thalès đảo).
Tương tự ta chứng minh được EM // AB.
Tứ giác DEMB có DE //BM và EM // DB nên tứ giác DEMB là hình bình hành (dấu hiệu nhận biết hình bình hành), suy ra DE = BM = .
Vậy DE // BC; DE = .
Chú ý: Trong một tam giác, nếu một đường thẳng đi qua trung điểm của một cạnh và song song với cạnh thứ hai thì nó đi qua trung điểm của cạnh thứ ba.
Ví dụ: Cho tam giác ABC với D, E lần lượt là trung điểm của AB, AC. Biết BC = 8 cm. Tính DE.
Hướng dẫn giải
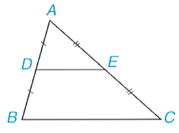
Ta có tam giác ABC có D, E lần lượt là trung điểm của AB, AC.
Do đó, DE là đường trung bình của tam giác ABC.
Suy ra: DE = = = 4 (cm).
Vậy DE = 4 cm.
Bài 1: Tính độ dài đoạn AE, biết DE // BC và AC = 8 cm.
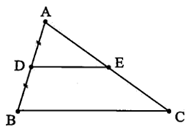
Hướng dẫn giải
Xét tam giác ABC, ta có: D là trung điểm AB và DE // BC
⇒ E là trung điểm của AC.
Suy ra: AE = .
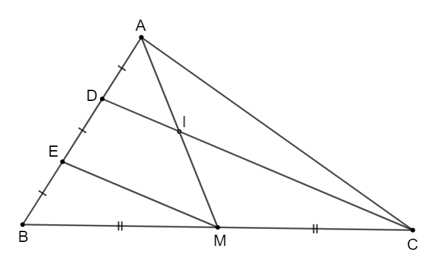
Bài 2: Cho tam giác ABC, điểm D thuộc cạnh AC sao cho AD = DC. Gọi M là trung điểm của BC, I là giao điểm của BD và AM. Chứng minh: AI = IM.
Hướng dẫn giải
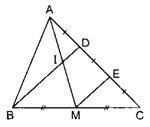
Gọi E là trung điểm của DC.
Trong ΔBDC, ta có:
M là trung điểm của BC (giả thiết).
E là trung điểm của CD (ta gọi).
Nên ME là đường trung bình của ∆BCD.
⇒ ME // BD (tính chất đường trung bình tam giác).
Suy ra: DI // ME.
Lại có: AD = DC (giả thiết).
DE = DC (vì E là trung điểm của DC).
Suy ra AD = DE nên D là trung điểm của AE.
Xét tam giác AME có D là trung điểm của AE và DI // ME (cmt).
Suy ra I là trung điểm của AM (tính chất đường trung bình của tam giác)
Vậy AI = IM.
Bài 3: Cho tam giác ABC, đường trung tuyến AM. Gọi D là trung điểm của AM, E là giao điểm của BD và AC, F là trung điểm của EC. Tính tỉ số .
Hướng dẫn giải
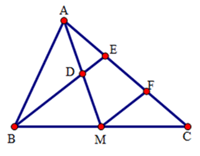
Xét ∆BEC có:
M là trung điểm của BC;
F là trung điểm của EC.
Do đó, MF là đường trung bình của ∆BEC.
Suy ra MF // BE.
Xét ∆AMF có:
D là trung điểm của AM;
DE // MF (do MF // BE).
Do đó, DE là đường trung bình của ∆AMF.
Suy ra E là trung điểm của AF nên AE = EF.
Mà EF = FC = EC (do F là trung điểm của EC)
Do vậy, AE = EF = FC = EC.
Suy ra .
Các bài học để học tốt Đường trung bình của tam giác Toán lớp 8 hay khác:
Với 15 bài tập trắc nghiệm Đường trung bình của tam giác Toán lớp 8 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 8.
Nội dung đang được cập nhật ...
Xem thêm bài tập trắc nghiệm Toán lớp 8 Kết nối tri thức có đáp án hay khác: