Với giải bài tập Toán 8 Bài tập cuối chương 3 trang 74, 75 sách Kết nối tri thức hay nhất, chi tiết giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 Bài tập cuối chương 3.

Giải Toán 8 Kết nối tri thức Bài tập cuối chương 3 (trang 74, 75)

Video Giải Toán 8 Bài tập cuối chương 3 - Cô Vũ Chuyên (Giáo viên VietJack)

A. Trắc nghiệm

Giải Toán 8 trang 74

Bài 3.39 trang 74 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài tập cuối chương 3 - Kết nối tri thức

Bài 3.39 trang 74 Toán 8 Tập 1: Trong các khẳng định sau, khẳng định nào đúng?

A. Không có tứ giác nào mà không có góc tù.

B. Nếu tứ giác có ba góc nhọn thì góc còn lại là góc tù.

C. Nếu tứ giác có hai góc tù thì haigóc còn lại phải nhọn.

D. Không có tứ giác nào có ba góc tù.

Lời giải:

* Khẳng định A sai vì có xảy ra trường hợp tứ giác mà không có góc tù.

Chẳng hạn như hình chữ nhật có bốn góc vuông, tức là hình chữ nhật không có góc tù.

* Khẳng định B.

Tứ giác có ba góc nhọn thì tổng số đo của ba góc bé hơn: 90^o . 3 = 270^o.

Khi đó, góc còn lại sẽ lớn hơn: 360^o – 270^o = 90^o.

Do đó, góc còn lại là góc tù nên khẳng định B đúng.

* Khẳng định C sai vì có thể xảy ra trường hợp tứ giác có hai góc tù, một góc vuông và một góc nhọn.

Ví dụ: Tứ giác ABCD có $\hat{A} = 100 °; \hat{B} = 100 °; \hat{C} = 90 °; \hat{D} = 70 °$ .

* Khẳng định D sai vì có thể xảy ra trường hợp tứ giác có ba góc tù.

Ví dụ: Tứ giác MNPQ có $\hat{M} = 100 °; \hat{N} = 110 °; \hat{P} = 120 °; \hat{Q} = 30 °$ .

Vậy khẳng định B là đúng.

Lời giải bài tập Toán 8 Bài tập cuối chương 3 hay, chi tiết khác:

Bài 3.40 trang 74 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài tập cuối chương 3 - Kết nối tri thức

Bài 3.40 trang 74 Toán 8 Tập 1: Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?

a) Tứ giác có hai đường chéo bằng nhau là hình bình hành.

b) Tứ giác có hai cặp cạnh bằng nhau là hình bình hành.

c) Tứ giác có ba góc vuông là hình chữ nhật.

d) Tứ giác có ba cạnh bằng nhau là hình thoi.

Lời giải:

• Khẳng định a) sai vì tứ giác có hai đường chéo bằng nhau thì chưa chắc tứ giác đó là hình bình hành.

• Khẳng định b) sai vì tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành, còn tứ giác có hai cặp cạnh bằng nhau thì chưa khẳng định được là hình bình hành.

• Khẳng định c) đúng.

Tứ giác có ba góc vuông thì số đo của góc còn lại là:

360^o – 90^o . 3 = 90^o.

Khi đó, số đo của góc còn lại cũng là góc vuông.

Do đó, tứ giác đã cho có bốn góc vuông nên tứ giác đó là hình chữ nhật.

• Khẳng định d) sai vì tứ giác có bốn cạnh bằng nhau mới là hình thoi.

Vậy khẳng định c) đúng; các khẳng định a), b), d) sai.

Lời giải bài tập Toán 8 Bài tập cuối chương 3 hay, chi tiết khác:

Bài 3.41 trang 74 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài tập cuối chương 3 - Kết nối tri thức

Bài 3.41 trang 74 Toán 8 Tập 1: Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?

a) Tứ giác có hai đường chéo bằng nhau và hai cạnh đối nào cũng bằng nhau là hình chữ nhật.

b) Tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành.

c) Tứ giác có hai cạnh song song và hai đường chéo bằng nhau là hình thang cân.

d) Tứ giác có hai cạnh song song và hai cạnh còn lại bằng nhau là hình bình hành.

Lời giải:

a) Tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành.

Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

Nên tứ giác có hai đường chéo bằng nhau và hai cạnh đối nào cũng bằng nhau là hình chữ nhật.

Do đó khẳng định a) đúng.

b) Tứ giác có hai cặp cạnh đối diện bằng nhau là hình bình hành.

Nên tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành.

Do đó khẳng định b) là đúng.

c) Tứ giác có hai cạnh song song là hình thang.

Hình thang có và hai đường chéo bằng nhau là hình thang cân.

Nên tứ giác có hai cạnh song song và hai đường chéo bằng nhau là hình thang cân.

Do đó khẳng định c) đúng.

d) Tứ giác có hai cạnh song song và hai cạnh còn lại bằng nhau nhưng không song song thì không là hình bình hành.

Do đó khẳng định d) sai.

Vậy các khẳng định a), b), c) đúng; khẳng định d) sai.

Lời giải bài tập Toán 8 Bài tập cuối chương 3 hay, chi tiết khác:

Bài 3.42 trang 74 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài tập cuối chương 3 - Kết nối tri thức

Bài 3.42 trang 74 Toán 8 Tập 1: Chứng minh rằng nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân (H.3.59).

Bài 3.42 trang 74 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Lời giải:

Bài 3.42 trang 74 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Gọi O là giao điểm của AC và BD.

Xét ∆ABC và ∆BAD có:

BC = AD (giả thiết)

AC = BD (giả thiết)

Cạnh AB chung

Do đó ∆ABC = ∆BAD (c.c.c)

Suy ra $\hat{A D B} = \hat{B C A}$ (hai góc tương ứng).

Xét ∆ACD và ∆BDC có:

AD = BC (giả thiết)

AC = BD (giả thiết)

Cạnh CD chung

Do đó ∆ADC = ∆BCD (c.c.c)

Suy ra $\hat{D A C} = \hat{C B D}$ (hai góc tương ứng).

Xét ∆OAD và ∆OBC có:

$\hat{A D B} = \hat{A C B}$ (chứng minh trên)

AD = BC (giả thiết)

$\hat{D A C} = \hat{C B D}$ (chứng minh trên)

Do đó ∆OAD = ∆OBC (g.c.g).

Suy ra OA = OB; OC = OD (các cặp cạnh tương ứng).

Khi đó, các tam giác OAB, OCD là tam giác cân tại O.

Suy ra $\hat{O A B} = \hat{O B A}; \hat{O C D} = \hat{O D C}$ .

Xét ∆OAB và ∆OCD cân tại O có:

• $\hat{A O B} = \hat{C O D}$ (hai góc đối đỉnh)

• $\hat{O A B} = \hat{O B A}; \hat{O C D} = \hat{O D C}$

• $\hat{O A B} + \hat{O B A} + \hat{A O B} = \hat{O C D} + \hat{O D C} + \hat{C O D} = 180 °$

$\hat{O A B} + \hat{O B A} = \hat{O C D} + \hat{O D C}$

$2 \hat{O A B} = 2 \hat{O C D}$

Suy ra $\hat{O A B} = \hat{O C D}$ mà hai góc này ở vị trí so le trong.

Do đó AB // CD.

Tứ giác ABCD có AB // CD nên ABCD là hình thang.

Hình thang ABCD có hai đường chéo AC = BD.

Do đó tứ giác ABCD là hình thang cân.

Vậy nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân.

Lời giải bài tập Toán 8 Bài tập cuối chương 3 hay, chi tiết khác:

Bài 3.43 trang 74 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài tập cuối chương 3 - Kết nối tri thức

Bài 3.43 trang 74 Toán 8 Tập 1: Cho hình bình hành ABCD. Lấy điểm P trên tia AB sao cho AP = 2AB.

a) Tứ giác BPCD có phải là hình bình hành không? Tại sao?

b) Khi tam giác ABD vuông cân tại A, hãy tính số đo các góc của tứ giác BPCD.

Lời giải:

Bài 3.43 trang 74 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Ta có AP = 2AB suy ra AB = BP = $\frac{A P}{2}$ .

Vì ABCD là hình bình hành nên:

• AB // CD hay BP // CD

• AB = CD mà AB = BP nên BP = CD.

Tứ giác BPCD có BP // CD; BP = CD

Do đó tứ giác BPCD là hình bình hành.

b) Khi tam giác ABD vuông cân tại A thì $\hat{A} = 90 °; \hat{A B D} = \hat{A D B} = 45 °$ .

Ta có $\hat{A B D} + \hat{D B P} = 180 °$ (hai góc kề bù).

Suy ra $\hat{D B P} = 180 ° - \hat{A B D} = 180 ° - 45 ° = 135 °$ .

Do đó $\hat{D C P} = \hat{D B P} = 135 °$ .

Vì tứ giác BPCD là hình bình hành nên BD // CP.

Suy ra $\hat{A B D} = \hat{P}$ (hai góc đồng vị).

Khi đó $\hat{P} = 45 °$ mà $\hat{P} = \hat{B D C}$ (vì tứ giác BPCD là hình bình hành).

Do đó $\hat{P} = \hat{B D C} = 45 °$ .

Vậy khi tam giác ABD vuông cân tại A thì số đo các góc của tứ giác BPCD là:

$\hat{D C P} = \hat{D B P} = 135 °$ ; $\hat{P} = \hat{B D C} = 45 °$ .

Lời giải bài tập Toán 8 Bài tập cuối chương 3 hay, chi tiết khác:

Bài 3.44 trang 75 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài tập cuối chương 3 - Kết nối tri thức

Bài 3.44 trang 75 Toán 8 Tập 1: Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC còn P, N lần lượt là chân đường vuông góc hạ từ M xuống CA, AB (H.3.60).

Bài 3.44 trang 75 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

a) Chứng minh hai tam giác vuông CMP và MBN bằng nhau.

b) Chứng minh tứ giác APMN là một hình chữ nhật.

Từ đó suy ra N là trung điểm của AB, P là trung điểm của AC.

c) Lấy điểm Q sao cho P là trung điểm của MQ, chứng minh tứ giác AMCQ là một hình thoi.

d) Nếu AB = AC, tức là tam giác ABC vuông cân tại A thì tứ giác AMCQ có là hình vuông không? Vì sao?

Lời giải:

a) Theo đề bài, AC ⊥ MP; AC ⊥ AB.

Suy ra MP // AB nên MP // BN.

Do đó $\hat{C M P} = \hat{C B A}$ (hai góc đồng vị).

Ta có P, N lần lượt là chân đường vuông góc hạ từ M xuống CA, AB

Nên $\hat{M P C} = \hat{B N M} = 90 °$ .

Xét ∆CMP và ∆MBN có:

$\hat{M P C} = \hat{B N M} = 90 °$

BM = CM (vì M là trung điểm của BC)

$\hat{C M P} = \hat{C B A}$ (chứng minh trên)

Do đó ∆CMP = ∆MBN (g.c.g).

b) Ta có $\hat{P A N} + \hat{A P M} + \hat{P M N} + \hat{M N A} = 360 °$

$90 ° + 90 ° + \hat{P M N} + 90 ° = 360 °$

$\hat{P M N} + 270 ° = 360 °$

Suy ra $\hat{P M N} = 360 ° - 270 ° = 90 °$ .

Tứ giác APMN có $\hat{P A N} = \hat{A P M} = \hat{P M N} = \hat{M N A} = 90 °$ .

Do đó, tứ giác APMN là một hình chữ nhật.

Suy ra MP = AN; AP = MN (các cặp cạnh tương ứng).

Mà MP = BN; CP = MN (vì ∆CMP = ∆MBN).

Do đó AP = CP; AN = BN.

Từ đó ta suy ra N là trung điểm của AB, P là trung điểm của AC.

c) Tứ giác AMCQ có:

MP = PQ (vì P là trung điểm của MQ)

AP = CP (vì P là trung điểm của AC)

Khi đó, tứ giác AMCQ có hai đường chéo AC và MQ cắt nhau tại trung điểm P của mỗi đường nên nó là hình bình hành.

Mà MQ ⊥ AC.

Do đó tứ giác AMCQ là một hình thoi.

d) Tứ giác APMN là một hình chữ nhật nên MP = AN.

Mà P là trung điểm MQ; N là trung điểm của AB.

Suy ra MQ = AB.

Lại có AB = AC (giả thiết) nên MQ = AC.

Tứ giác AMCQ có hai đường chéo AC và MQ bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm P của mỗi đường.

Do đó, tứ giác AMCQ có là hình vuông.

Lời giải bài tập Toán 8 Bài tập cuối chương 3 hay, chi tiết khác:

Bài 3.45 trang 75 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài tập cuối chương 3 - Kết nối tri thức

Bài 3.45 trang 75 Toán 8 Tập 1: Cho tam giác ABC cân tại A; M là một điểm thuộc đường thẳng BC, B ở giữa M và C. Gọi E, K lần lượt là chân đường vuông góc hạ từ M và từ B xuống AC, còn N, D lần lượt là chân đường vuông góc hạ từ B xuống MEvà từ M xuống AB (H.3.61).

Bài 3.45 trang 75 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Chứng minh rằng:

a) Tứ giác BKEN là hình chữ nhật.

b) BK bằng hiệu khoảng cách từ M đến AC và đến AB (dù M thay đổi trên đường thẳng BC miễn là B nằm giữa M và C) tức là BK = ME – MD.

Lời giải:

a) Vì ME ⊥ AC; BK ⊥ AC; BN ⊥ ME nên $\hat{N E K} = 90 °; \hat{B K E} = 90 °; \hat{B N E} = 90 °$ .

Suy ra $\hat{N B K} = 360 ° - \hat{N E K} - \hat{B K E} - \hat{B N E}$

$= 360 ° - 90 ° - 90 ° - 90 ° = 90 °$ .

Tứ giác BKEN có $\hat{N E K} = 90 °; \hat{B K E} = 90 °; \hat{B N E} = 90 °$ ; $\hat{N B K} = 90 °$ .

Do đó, tứ giác BKEN là hình chữ nhật.

b) Khoảng cách từ M đến AC và AB lần lượt là ME và MD.

Tứ giác BKEN là hình chữ nhật nên NE = BK (1)

Ta có BN ⊥ ME; CE ⊥ ME nên BN // EC.

Suy ra $\hat{M B N} = \hat{B C A}$ (hai góc đồng vị)

Mà $\hat{A B C} = \hat{B C A}$ (vì ∆ABC cân tại A); $\hat{A B C} = \hat{M B D}$ (hai góc đối đỉnh)

Do đó $\hat{M B N} = \hat{M B D}$ .

Xét ∆MBN và ∆MBD có:

$\hat{M N B} = \hat{D} = 90 °$

Cạnh BM chung

$\hat{M B N} = \hat{M B D}$ (chứng minh trên)

Do đó ∆MBN = ∆MBD (cạnh huyền – góc nhọn)

Suy ra MN = MD (hai cạnh tương ứng) (2)

Từ (1) và (2) suy ra: ME = MN + NE = MD + BK.

Do đó BK = NE = ME – BD.

Lời giải bài tập Toán 8 Bài tập cuối chương 3 hay, chi tiết khác:

SBT Toán 8 Kết nối tri thức Bài tập cuối chương 3

Với giải sách bài tập Toán 8 Bài tập cuối chương 3 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 8 dễ dàng làm bài tập trong SBT Toán 8 Bài tập cuối chương 3.

Giải SBT Toán 8 Kết nối tri thức Bài tập cuối chương 3

A. Câu hỏi (Trắc nghiệm)

Chọn phương án đúng trong mỗi câu sau:

Vở thực hành Toán 8 Bài tập cuối chương 3 - Kết nối tri thức

Với giải vở thực hành Toán 8 Bài tập cuối chương 3 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 8 dễ dàng làm bài tập về nhà trong VTH Toán 8 Bài tập cuối chương 3.

Giải vở thực hành Toán 8 Bài tập cuối chương 3 - Kết nối tri thức

A. CÂU HỎI TRẮC NGHIỆM

Chọn phương án đúng trong mỗi câu sau:

Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

Tổng hợp lý thuyết Toán 8 Chương 3: Tứ giác sách Kết nối tri thức hay nhất, chi tiết cùng các bài tập có lời giải sẽ giúp học sinh lớp 8 nắm vững kiến thức trọng tâm Toán 8 Chương 3.

Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

Lý thuyết tổng hợp Toán 8 Chương 3

1. Tứ giác lồi

+ Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC , CD, DA trong đó không có hai đoạn thẳng nào nằm trên cùng một đoạn thẳng.

Ví dụ: Hình a, b, c là tứ giác, hình d không phải là tứ giác.

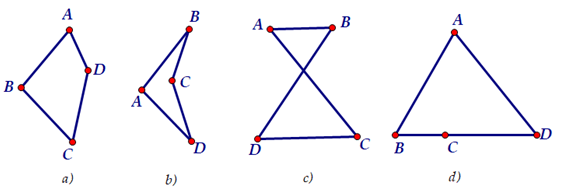
Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

Trong tứ giác ABCD, các điểm A, B, C, D là các đỉnh, các đoạn thẳng AB, BC, CD, DA là các cạnh.

+ Tứ giác lồi là tứ giác mà hai đỉnh thuộc một cạnh bất kì luôn nằm về một phía của đường thẳng đi qua hai đỉnh còn lại (Hình a ở ví dụ 1 là tứ giác lồi, hình b, c không phải tứ giác lồi).

+ Trong tứ giác lồi, các góc ABC, BCD, CDA, DAB gọi là các góc của tứ giác và kí hiệu đơn giản lần lượt là $\hat{B}, \hat{C}, \hat{D}, \hat{A} .$

Chú ý:

+ Từ nay, khi nói đến tứ giác mà không giải thích gì thêm, ta hiểu đó là tứ giác lồi.

+ Tứ giác ABCD trong hình a còn được gọi tên là tứ giác BCDA, CDAB, DABC, ADCB, DCBA, CBAD, BADC.

2. Tổng các góc của một tứ giác

+ Định lí: Tổng các góc trong một tứ giác bằng 360°.

3. Hình thang. Hình thang cân

3.1. Khái niệm hình thang, hình thang cân

+ Hình thang là tứ giác có hai cạnh đối song song.

+ Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

Xét các hình dưới đây:

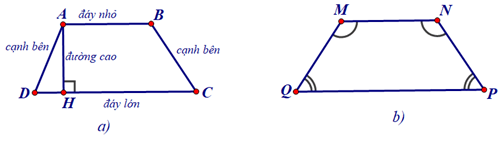
Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

+ Hình a là hình thang ABCD (AB // CD). Hai cạnh song song gọi là hai đáy, hai cạnh còn lại gọi là hai cạnh bên, đường vuông góc AH kẻ từ A đến CD gọi là một đường cao của hình thang ABCD.

+ Hình b là hình thang cân MNPQ (MN // PQ)

Hai góc M, N kề đáy nhỏ MN, $\hat{M} = \hat{N}$

Hai góc C, D kề đáy lớn CD, $\hat{C} = \hat{D}$ .

Chú ý: Trong hình thang, hai góc kề một đáy bằng nhau thì hai góc kề đáy kia cũng bằng nhau.

3.2. Tính chất của hình thang cân

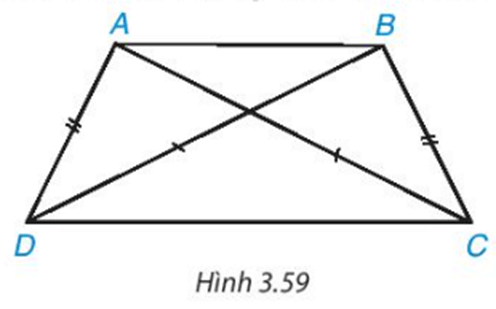
+ Định lí 1: Trong hình thang cân, hai cạnh bên bằng nhau.

+ Định lí 2: Trong hình thang cân, hai đường chéo bằng nhau.

3.3.Dấu hiệu nhận biết

+ Định lí 3 (Dấu hiệu nhận biết hình thang cân): Nếu một hình thang có hai đường chéo bằng nhau thì đó là hình thang cân.

Chú ý: Định lí 3 là định lí đảo của định lí 2. Giả thiết của định lí này là kết luận của định lí kia.

4. Hình bình hành

4.1. Khái niệm hình bình hành và tính chất

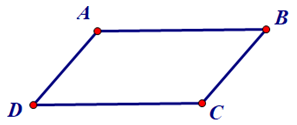
+ Định nghĩa: Hình bình hành là tứ giác có các cạnh đối song song.

Tứ giác ABCD là hình bình hành có AB // CD và AD // BC.

Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

+ Định lí 1 (Tính chất của hình bình hành)

Trong hình bình hành:

a) Các cạnh đối bằng nhau;

b) Các góc đối bằng nhau;

c) Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Nhận xét: Trong hình bình hành, hai góc kề một cạnh bất kì thì bù nhau.

4.2. Dấu hiệu nhận biết hình bình hành

+ Định lí 2 (Dấu hiệu nhận biết hình bình hành theo cạnh):

a) Tứ giác có các cạnh đối bằng nhau là một hình bình hành.

b) Tứ giác có một cặp cạnh đối song song và bằng nhau là một hình bình hành.

+ Định lí 3 (Dấu hiệu nhận biết hình bình hành theo góc và đường chéo):

a) Tứ giác có các góc đối bằng nhau là một hình bình hành.

b) Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là một hình bình hành.

5. Hình chữ nhật

5.1. Khái niệm và tính chất của hình chữ nhật

+ Định nghĩa:Hình chữ nhật là tứ giác có bốn góc vuông.

Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

Tứ giác ABCD có $\hat{A} = \hat{B} = \hat{C} = \hat{D} = 90 °$ , nó là hình chữ nhật.

Chú ý: Nếu một tứ giác có ba góc vuông thì góc còn lại cũng là góc vuông và tứ giác đó là hình chữ nhật.

+ Định lí 1: Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.

Chú ý: Hình chữ nhật có tất cả các tính chất của hình bình hành và của hình thang cân.

+ Nhận xét: Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.

5.2. Dấu hiệu nhận biết hình chữ nhật

+ Định lí 2 (Dấu hiệu nhận biết hình chữ nhật):

a) Hình bình hành có một góc vuông là hình chữ nhật.

b) Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

Nhận xét: Nếu tam giác có một đường trung tuyến bằng nửa cạnh tương ứng thì tam giác đó là tam giác vuông.

6. Hình thoi

6.1. Khái niệm và tính chất của hình thoi

+ Định nghĩa: Hình thoi là tứ giác có bốn cạnh bằng nhau.

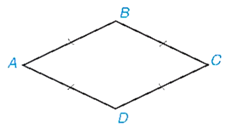
Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

Tứ giác ABCD có AB = BC = CD = DA, nó là một hình thoi.

Chú ý: Hình thoi có tất cả các tính chất của hình bình hành.

+ Định lí 1: Trong hình thoi:

a) Hai đường chéo vuông góc với nhau;

b) Hai đường chéo là các đường phân giác của các góc trong hình thoi.

6.2. Dấu hiệu nhận biết hình thoi

Định lí 2:

a) Hình bình hành có hai cạnh kề bằng nhau là hình thoi.

b) Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

c) Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.

7. Hình vuông

7.1. Khái niệm hình vuông và tính chất của nó

+ Định nghĩa: Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.

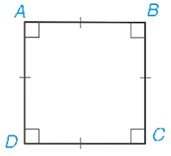
Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

Tứ giác ABCD có $\hat{A} = \hat{B} = \hat{C} = \hat{D} = 90 °$ và AB = BC = CD = DA, nó là hình vuông.

+ Định lí 3: Trong một hình vuông, hai đường chéo bằng nhau, vuông góc với nhau, cắt nhau tại trung điểm mỗi đường và là các đường phân giác của các góc của hình vuông.

Chú ý: Hình vuông cũng là hình chữ nhật, hình thoi nên nó có tất cả các tính chất của hình chữ nhật và hình thoi.

7.2. Dấu hiệu nhận biết hình vuông

Định lí 4:

a) Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

b) Hình chữ nhật có hai đường chéo vuông góc là hình vuông.

c) Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.

Chú ý:

- Hình thoi có một góc vuông là hình vuông.

- Hình thoi có hai đường chéo bằng nhau là hình vuông.

Bài tập tổng hợp Toán 8 Chương 3

Bài 1. Tính góc chưa biết của các tứ giác trong hình sau:

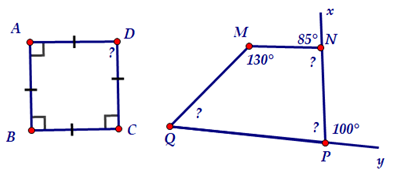
Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

Hướng dẫn giải

+ Tứ giác ABCD có 3 góc vuông nên $\hat{A} = \hat{B} = \hat{C} = 90 °$ . Theo định lí về tổng các góc trong một tứ giác ta có: $\hat{A} + \hat{B} + \hat{C} + \hat{D} = 360 °$

Suy ra $\hat{D} = 360 ° - (\hat{A} + \hat{B} + \hat{C}) = 360 ° - (90 ° + 90 ° + 90 °) = 90 ° .$

+ Vì $\hat{M N x} + \hat{M N P} = 180 °$ (hai góc kề bù) $\Rightarrow \hat{M N P} = 180 ° - 85 ° = 95 ° .$

$\hat{N P y} + \hat{N P Q} = 180 °$ (hai góc kề bù) $\Rightarrow \hat{N P Q} = 180 ° - 100 ° = 80 ° .$

Theo định lí về tổng các góc trong một tứ giác ta có: $\hat{M} + \hat{M N P} + \hat{N P Q} + \hat{Q} = 360 °$

Suy ra $\hat{Q} = 360 ° - (\hat{M} + \hat{M N P} + \hat{N P Q}) = 360 ° - 130 ° - 95 ° - 80 ° = 55 °$ .

Bài 2. Tính góc chưa biết của tứ giác trong hình dưới đây, biết $\hat{I} + \hat{K} = 180 °$ .

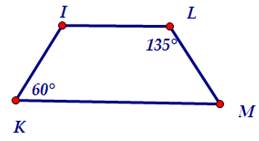
Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

Hướng dẫn giải

Vì $\hat{I} + \hat{K} = 180 °$ mà $\hat{K} = 60 ° \Rightarrow \hat{I} = 120 °$

Theo định lí về tổng các góc trong một tứ giác ta có:

$\hat{I} + \hat{K} + \hat{M} + \hat{L} = 360 ° \Rightarrow \hat{M} = 360 ° - (\hat{I} + \hat{K} + \hat{L}) = 360 ° - (120 ° + 60 ° + 135 °) = 45 °$ .

Bài 3. Tứ giác MNEF có MN = MF, NE = FE, được gọi là hình cái diều.

a) Chứng minh ME là đường trung trực của đoạn thẳng NF.

b) Tính các góc E, F biết $\hat{M} = 100 °, \hat{N} = 105 ° .$

Hướng dẫn giải

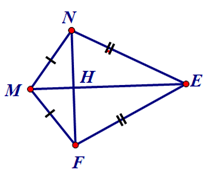
Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

a) Xét $Δ M N E$ và $Δ M F E$ có:

MN = MF (giả thiết)

NE = FE (giả thiết)

ME chung

Do đó $Δ M N E$ = $Δ M F E$ (cạnh - cạnh - cạnh) $\Rightarrow \hat{F M E} = \hat{N M E}$

Gọi H là giao điểm của ME và NF

Xét $Δ M N H$ và $Δ M F H$ có:

MN = MF ( giả thiết)

$\hat{F M E} = \hat{N M E}$ (chứng minh trên)

MH chung

Do đó $Δ M N H$ = $Δ M F H$ (cạnh - góc - cạnh)

$\Rightarrow N H = F H$ (1)

Và $\hat{M H N} = \hat{M H F}$ mà $\hat{M H N} + \hat{M H F} = 180 ° \Rightarrow \hat{M H N} = \hat{M H F} = 90 °$

$\Rightarrow M E ⊥ N F$ (2)

Từ (1) và (2) suy ra ME là đường trung trực của đoạn thẳng NF.

b) Vì $Δ M N E = Δ M F E \Rightarrow \hat{M N E} = \hat{M F E} = 105 °$

Theo định lí về tổng các góc trong một tứ giác suy ra $\hat{N E F} = 50 °$ .

Bài 4. Hình thang ABCD (AB // CD) trong hình bên dưới có phải hình thang cân không? Vì sao?

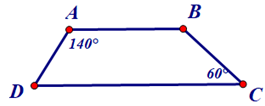
Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

Hướng dẫn giải

Giả sử ABCD (AB // CD) là hình thang cân.

Khi đó, ta có: $\hat{A} = \hat{B} = 140 °, \hat{C} = \hat{D} = 60 °$ .

Tổng 4 góc trong hình thang ABCD là $\hat{A} + \hat{B} + \hat{C} + \hat{D} = 400 ° > 360 °$ .

Suy ra ABCD không phải là hình thang cân.

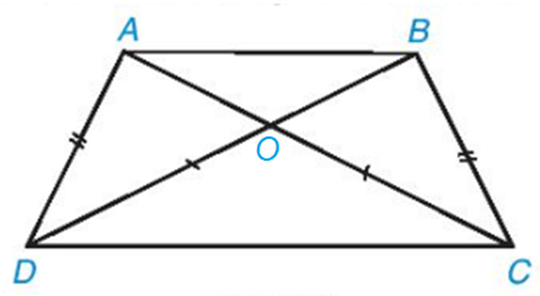
Bài 5. Cho hình thang MNPQ (MN // PQ) có $\hat{N M P} = \hat{M N Q},$ E là giao điểm của MP và NQ. Chứng minh hình thang MNPQ là hình thang cân.

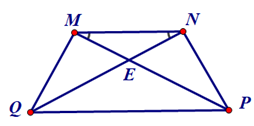
Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

Hướng dẫn giải

Vì MN // QP nên $\hat{N M P} = \hat{M P Q}$ và $\hat{N Q P} = \hat{M N Q}$ (các cặp góc so le trong)

Mà $\hat{N M P} = \hat{M N Q} \Rightarrow \hat{N M P} = \hat{M P Q} = \hat{N Q P} = \hat{M N Q}$ .

$Δ M N E$ có $\hat{N M P} = \hat{M N Q}$ nên $Δ M N E$ cân tại E

Suy ra ME = NE (1)

$Δ Q E P$ có $\hat{M P Q} = \hat{N Q P}$ nên $Δ Q E P$ cân tại E

Suy ra EQ = EP (2)

Từ (1) và (2) ta có: ME + EP = NE + EQ hay MP = NQ

Suy ra MNPQ là hình thang cân (dấu hiệu nhận biết).

Bài 6. Cho hình thang cân ABCD (AB // CD) có các đường cao AE, BF. Chứng minh DE = CF.

Hướng dẫn giải

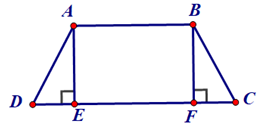
Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

Vì ABCD (AB // CD) là hình thang cân nên và AD = BC.

Xét $Δ A E D$ và $Δ B F C$ có:

$\hat{A E D} = \hat{B F C} = 90 ° (A E ⊥ D C, B F ⊥ D C)$

$\hat{D} = \hat{C}$ (chứng minh trên)

AD = BC (chứng minh trên)

Do đó $Δ A E D = Δ B F C$ (cạnh huyền - góc nhọn)

Suy ra DE = CF (cạnh tương ứng bằng nhau).

Bài 7. Tính các góc còn lại của hình bình hành ABCD trong hình dưới đây.

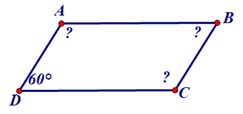
Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

Vì tứ giác ABCD là hình bình hành nên $\hat{B} = \hat{D} = 60 °$

Theo định lí tổng các góc trong một tứ giác ta có:

$\hat{A} + \hat{B} + \hat{C} + \hat{D} = 360 °$ suy ra $\hat{A} + \hat{C} = 240 ° \Rightarrow \hat{A} = \hat{C} = 120 °$ .

Bài 8. Trong mỗi trường hợp sau, tứ giác nào là hình bình hành, tứ giác nào không phải là hình bình hành? Vì sao?

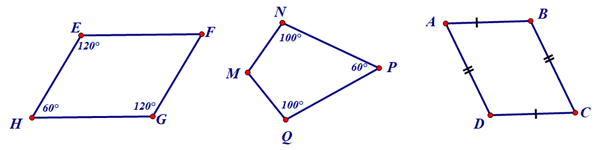
Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

Hướng dẫn giải

+ Tứ giác EFGH có $\hat{F} = 360 ° - (\hat{E} + \hat{H} + \hat{G}) = 60 °$

Suy ra $\hat{F} = \hat{H}$ mà $\hat{G} = \hat{E}$ nên theo dấu hiệu nhận biết của hình bình hành ta có tứ giác EFGH là hình bình hành.

+ Tứ giác MNPQ không là hình bình hành vì ta dễ dàng tính được $\hat{M} = 100 ° \neq \hat{P}$

+ Tứ giác ABCD là hình bình hành vì có các cạnh đối bằng nhau: AB = CD và AD = BC.

Bài 9. Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Một đường thẳng đi qua O lần lượt cắt các cạnh AB, CD của hình bình hành tại hai điểm M, N. Chứng minh $Δ O A M = Δ O C N .$ Từ đó suy ra tứ giác MBND là hình bình hành.

Hướng dẫn giải

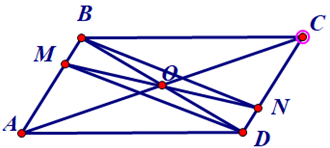
Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

+ Vì O là giao điểm của hai đường chéo của hình bình hành ABCD nên O là trung điểm của BD và AC.

Lại có: AB // CD nên $\hat{O C N} = \hat{O A M}$ (hai góc so le trong)

+ Xét $Δ O A M$ và $Δ O C N$ có:

$\hat{O C N} = \hat{O A M}$ (chứng minh trên)

OA = OC (O là trung điểm AC)

$\hat{A O M} = \hat{C O N}$ (hai góc đối đỉnh)

Do đó $Δ O A M = Δ O C N$ (góc - cạnh - góc)

Suy ra OM = ON hay O là trung điểm MN.

+ Xét tứ giác MBND có hai đường chéo MN và BD cắt nhau tại trung điểm O của mỗi đường, suy ra tứ giác MBND là hình bình hành (dấu hiệu nhận biết).

Bài 10. Cho tam giác ABC, đường cao AH. Gọi I là trung điểm cạnh AC, E là điểm đối xứng với H qua I. Chứng minh tứ giác AHCE là hình chữ nhật.

Hướng dẫn giải

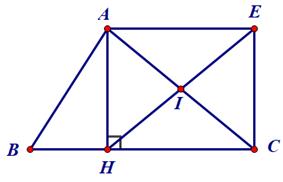
Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

+ Tam giác AHC vuông tại H có đường trung tuyến HI (do I là trung điểm của AC) ứng với cạnh huyền AC nên $H I = \frac{1}{2} A C$ (trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền).

+ Vì E đối xứng với H qua I nên IE = $H I = \frac{1}{2} A C$ suy ra IA = IC = IE = HI.

Suy ra HE = AC.

+ Xét tứ giác AHCE có hai đường chéo AC và HE cắt nhau tại trung điểm I của mỗi đường nên tứ giác AHCE là hình bình hành. Mặt khác ta có HE = AC (chứng minh trên) nên AHCE là hình chữ nhật.

Bài 11. Cho tam giác ABC vuông cân tại C, M là điểm bất kì trên cạnh AB. Vẽ ME vuông góc với AC tại E, MF vuông góc với BC tại F. Chứng minh tứ giác CFME là hình chữ nhật.

Hướng dẫn giải

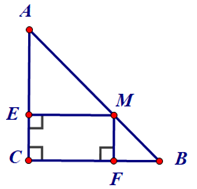
Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

Vì ME vuông góc với AC tại E, MF vuông góc với BC tại F và tam giác ABC vuông cân tại C nên $\hat{M E C} = \hat{M F C} = \hat{C} = 90 °$ hay tứ giác CEMF có ba góc vuông, suy ra tứ giác CEMF là hình chữ nhật.

Bài 12. Cho hình bình hành ABCD có AC vuông góc với AD. Gọi E, F theo thứ tự là trung điểm của các cạnh AB, CD. Chứng minh tứ giác AECF là hình thoi.

Hướng dẫn giải

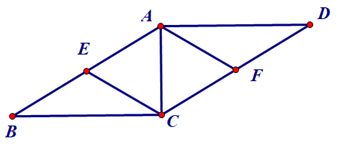
Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

Vì hình bình hành ABCD có AC vuông góc với AD nên $\hat{C A D} = \hat{A C B} = 90 °$ .

Xét tam giác vuông CAD vuông tại A có AF là đường trung tuyến ứng với cạnh huyền CD.

Suy ra $A F = \frac{1}{2} C D \Rightarrow A F = F C = F D = \frac{1}{2} C D$ (1)

Tương tự xét tam giác vuông ACB vuông tại C có CE là đường trung tuyến ứng với cạnh huyền AB.

$\Rightarrow C E = \frac{1}{2} A B \Rightarrow E C = A E = E B = \frac{1}{2} A B$ (2)

Lại có: AB = CD (tính chất hình bình hành) (3)

Từ (1), (2) và (3) suy ra AE = CE = CF = FA

Suy ra tứ giác AECF là hình thoi.

Bài 13. Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy hai điểm D, E sao cho BD = DE = EC. Qua D và E kẻ các đường vuông góc với BC, chúng cắt AB, AC lần lượt ở K và H. Tứ giác KHED là hình gì? Vì sao?

Hướng dẫn giải

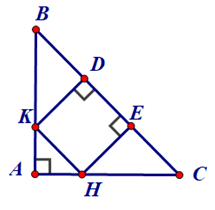
Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

Vì tam giác ABC vuông cân tại A nên $\hat{B} = \hat{C} = 45 °$ .

Tam giác DBK vuông tại D có $\hat{B} = 45 °$ nên tam giác DBK vuông cân tại D.

Suy ra BD = DK (1)

Chứng minh tương tự ta cũng có tam giác EHC vuông cân tại E.

Suy ra EH = EC (2)

Lại có: BD = DE = EC (gt) (3)

Từ (1), (2) và (3) suy ra KD = DE = HE

Tứ giác KHED có KD // HE (cùng vuông góc với BC) và KD = HE nên tứ giác KHED là hình bình hành.

Mặt khác hình bình hành KHED có hai cạnh bên KD = DE nên KHED là hình thoi.

Mà hình thoi KHED có góc KDE là góc vuông (do giả thiết KD vuông góc BC) nên KHED là hình vuông.

Học tốt Toán 8 Chương 3

Các bài học để học tốt Tổng hợp lý thuyết Toán 8 Chương 3 Toán lớp 8 hay khác:

Toán 8 Kết nối tri thức Bài tập cuối chương 3 (trang 74, 75)

Mục lục

Giải Toán 8 Kết nối tri thức Bài tập cuối chương 3 (trang 74, 75)

Bài 3.39 trang 74 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài tập cuối chương 3 - Kết nối tri thức

Bài 3.40 trang 74 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài tập cuối chương 3 - Kết nối tri thức

Bài 3.41 trang 74 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài tập cuối chương 3 - Kết nối tri thức

Bài 3.42 trang 74 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài tập cuối chương 3 - Kết nối tri thức

Bài 3.43 trang 74 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài tập cuối chương 3 - Kết nối tri thức

Bài 3.44 trang 75 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài tập cuối chương 3 - Kết nối tri thức

Bài 3.45 trang 75 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài tập cuối chương 3 - Kết nối tri thức

SBT Toán 8 Kết nối tri thức Bài tập cuối chương 3

Giải SBT Toán 8 Kết nối tri thức Bài tập cuối chương 3

Vở thực hành Toán 8 Bài tập cuối chương 3 - Kết nối tri thức

Giải vở thực hành Toán 8 Bài tập cuối chương 3 - Kết nối tri thức

Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

Tổng hợp lý thuyết Toán 8 Chương 3 Kết nối tri thức

Lý thuyết tổng hợp Toán 8 Chương 3

Bài tập tổng hợp Toán 8 Chương 3

Học tốt Toán 8 Chương 3

Mở đầu trang 5 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

HĐ1 trang 6 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

HĐ2 trang 6 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Luyện tập 1 trang 6 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Toán 8 Kết nối tri thức Luyện tập chung (trang 17, 18)

Tranh luận trang 6 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Câu hỏi trang 7 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Luyện tập 2 trang 8 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

HĐ3 trang 8 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Toán 8 Kết nối tri thức Luyện tập chung (trang 25, 26)