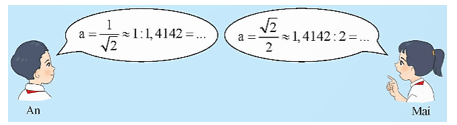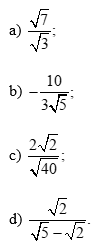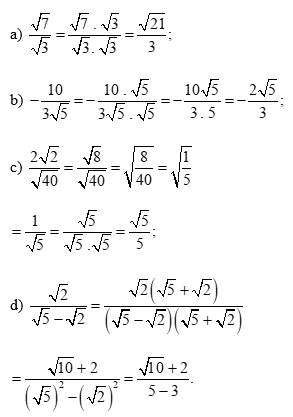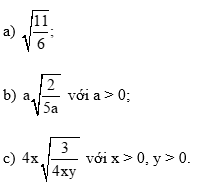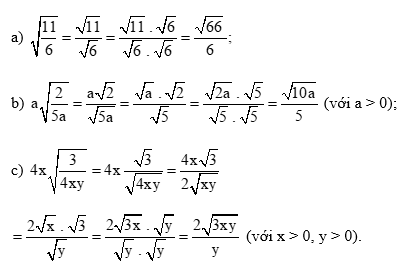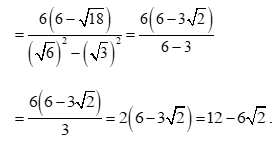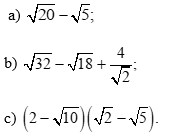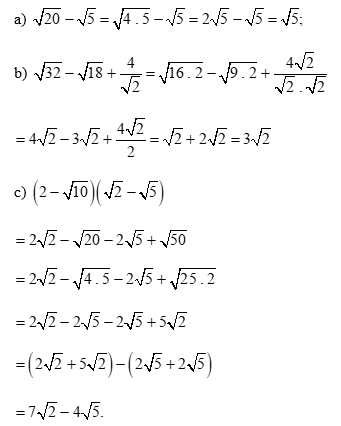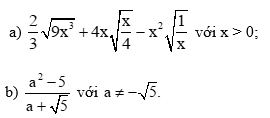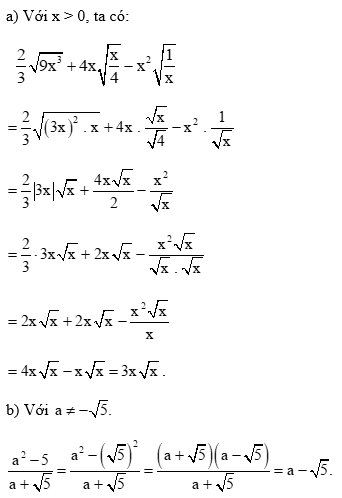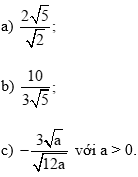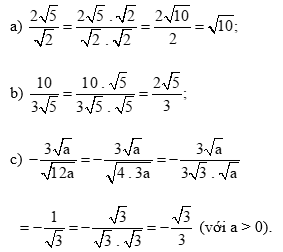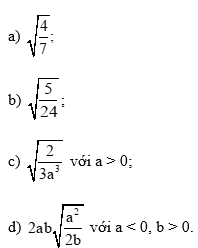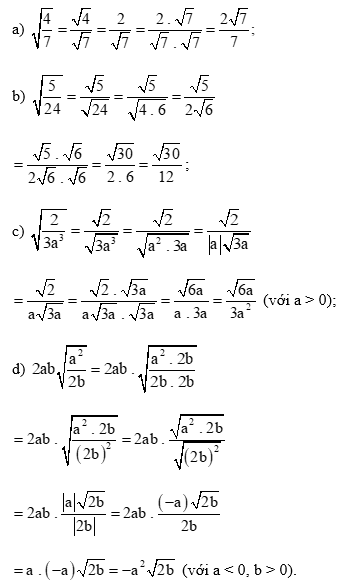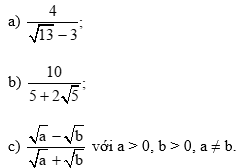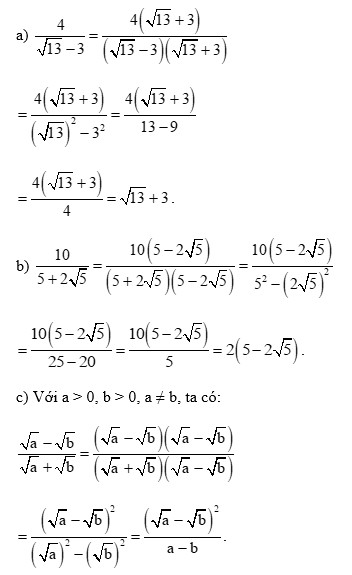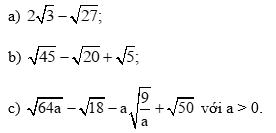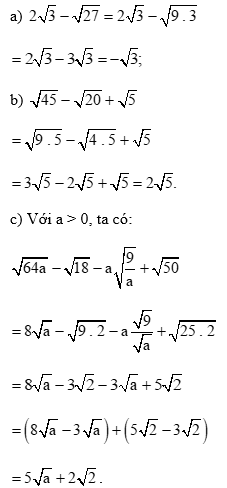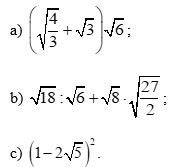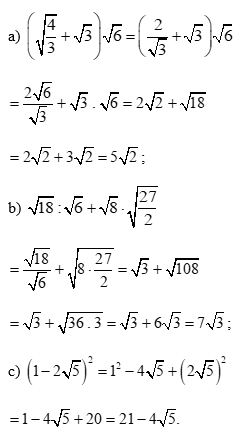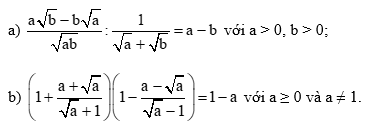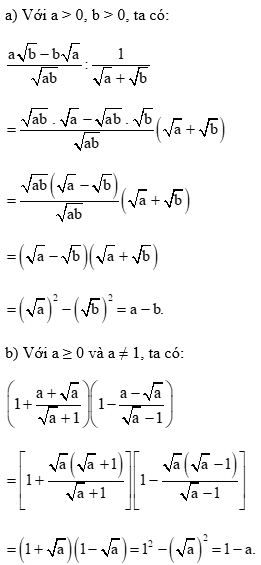Với giải bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh lớp 9 dễ dàng làm bài tập Toán 9 Bài 4.

Giải Toán 9 Chân trời sáng tạo Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai

Giải Toán 9 trang 52

Khởi động trang 52 Toán 9 Tập 1 Chân trời sáng tạo

Giải Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai - Chân trời sáng tạo

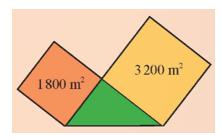
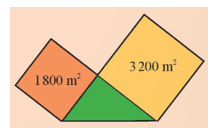
Khởi động trang 52 Toán 9 Tập 1: Một khu đất hình tam giác vuông tiếp giáp hai thửa ruộng hình vuông có diện tích như hình bên. Khu đất hình tam giác vuông có chu vi bằng chu vi thửa ruộng bé không? Kiểm tra bằng cách nào?

Lời giải:

Sau bài học này ta giải quyết được bài toán như sau:

• Hình vuông bé (màu cam) có diện tích là 1 800 m².

Khi đó, cạnh thửa ruộng bé hình vuông là: $\sqrt{1 800}= \sqrt{900. 2}= 30\sqrt{2}$ (m).

Chu vi thửa ruộng bé là: $30\sqrt{2} . 4= 120\sqrt{2}$(m).

• Hình vuông lớn có diện tích (màu vàng) là 3 200 m².

Khi đó, cạnh thửa ruộng lớn hình vuông là: $\sqrt{3 200}= \sqrt{1 600 . 2}= 40\sqrt{2}$.

• Hình tam giác vuông (màu xanh) có hai cạnh góc vuông là hai cạnh của của hai hình vuông trong hình vẽ trên.

Áp dụng định lí Pythagore vào tam giác vuông (màu xanh), ta có:

Độ dài cạnh huyền của tam giác vuông (màu xanh) là:

${\left(30\sqrt{2}\right)}^2 + {\left(40\sqrt{2}\right)}^2 = \sqrt{1 800 + 3 200}$

=$\sqrt{5 000}= \sqrt{2 500. 2}= 50\sqrt{2}$ (m).

Chu vi tam giác vuông là: $30\sqrt{2} + 40\sqrt{2} + 50\sqrt{2} = 120\sqrt{2} \left(m\right)$.

Vậy khu đất hình tam giác vuông có chu vi bằng chu vi thửa ruộng bé.

Lời giải bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay, chi tiết khác:

Khám phá 1 trang 52 Toán 9 Tập 1 Chân trời sáng tạo

Giải Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai - Chân trời sáng tạo

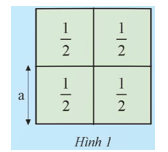
Khám phá 1 trang 52 Toán 9 Tập 1: Bốn ô vuông diện tích $\frac{1}{2}{m}^2$ ghép thành cửa sổ như Hình 1.

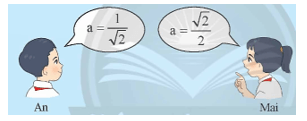
a) Hai bạn An và Mai tính độ dài cạnh a (m) của mỗi ô cửa.

Kết quả của mỗi bạn có đúng không? Giải thích.

b) Biết rằng $\sqrt{2}\approx 1,4142$  Không dùng máy tính cầm tay, hai bạn tìm giá trị gần đúng của độ dài mỗi ô cửa.

Theo em, bạn nào sẽ tìm ra đáp số nhanh hơn?

Lời giải:

a) Diện tích mỗi hình vuông là: $S = \frac{1}{2}{m}^2$.

Mà S = a² suy ra $a = \sqrt{S} = \sqrt{\frac{1}{2}} = \frac{1}{\sqrt{2}}\left(m\right)$.

Ta thấy $\frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{\sqrt{2}. \sqrt{2}}= \frac{\sqrt{2}}{2}$.

Vậy kết quả của 2 bạn đều đúng.

b) Cách tính của bạn An là $a = \frac{1}{\sqrt{2}}$ , ta tính bằng cách tính căn bậc hai và một phép tính nghịch đảo.

Cách tính của bạn Mai là $a = \frac{\sqrt{2}}{2}$ , ta tính bằng cách tính căn bậc hai và một phép tính chia.

Do đó, bạn Mai sẽ tìm ra đáp số nhanh hơn vì phép chia cho số tự nhiên sẽ thực hiện nhanh hơn phép tính nghịch đảo của một số vô tỉ.

Lời giải bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay, chi tiết khác:

Thực hành 1 trang 54 Toán 9 Tập 1 Chân trời sáng tạo

Giải Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai - Chân trời sáng tạo

Thực hành 1 trang 54 Toán 9 Tập 1: Trục căn thức ở mẫu các biểu thức sau:

Lời giải:

Lời giải bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay, chi tiết khác:

Thực hành 2 trang 54 Toán 9 Tập 1 Chân trời sáng tạo

Giải Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai - Chân trời sáng tạo

Thực hành 2 trang 54 Toán 9 Tập 1: Khử mẫu của biểu thức lấy căn:

Lời giải:

Lời giải bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay, chi tiết khác:

Vận dụng 1 trang 54 Toán 9 Tập 1 Chân trời sáng tạo

Giải Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai - Chân trời sáng tạo

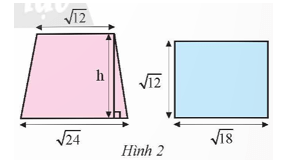
Vận dụng 1 trang 54 Toán 9 Tập 1: Biết rằng hình thang và hình chữ nhật ở Hình 2 có diện tích bằng nhau. Tính chiều cao h của hình thang.

Lời giải:

Diện tích hình chữ nhật là:

$\sqrt{18}.\sqrt{12}=\sqrt{18.12}=\sqrt{18.2.6}=\sqrt{36.6}=6\sqrt{6}$(đvdt).

Vì hình thang và hình chữ nhật ở Hình 2 có diện tích bằng nhau nên diện tích hình thang bằng $6\sqrt{6}$(đvdt).

Khi đó, diện tích hình thang là: $\frac{\sqrt{24}+ \sqrt{12}}{2}.h= 6\sqrt{6}$.

Ta có $\frac{\sqrt{24}+ \sqrt{12}}{2}=\frac{\sqrt{4.6}+\sqrt{4.3}}{2}$

$=\frac{2\sqrt{6}+2\sqrt{3}}{2}=\frac{2\left(\sqrt{6}+\sqrt{3}\right)}{2}=\sqrt{6}+\sqrt{3}$.

Do đó,$\left(\sqrt{6}+\sqrt{3}\right).h=6\sqrt{6}$

Suy ra  h = $\frac{6\sqrt{6}}{\sqrt{6}+\sqrt{3}}=\frac{6\sqrt{6}\left(\sqrt{6}-\sqrt{3}\right)}{\left(\sqrt{6}+\sqrt{3}\right)\left(\sqrt{6}-\sqrt{3}\right)}$

Vậy chiều cao h của hình thang $h = 12 - 6\sqrt{2}$.

Lời giải bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay, chi tiết khác:

Khám phá 2 trang 54 Toán 9 Tập 1 Chân trời sáng tạo

Giải Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai - Chân trời sáng tạo

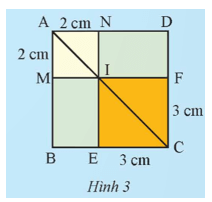
Khám phá 2 trang 54 Toán 9 Tập 1: Hình vuông ABCD được chia thành hai hình vuông và hai hình chữ nhật như Hình 3.

a) Tính độ dài đường chéo của hai hình vuông AMIN và CEIF.

b) Tính độ dài đường chéo của hình vuông ABCD theo hai cách khác nhau.

Lời giải:

a) Vì AMIN là hình vuông nên AM = IN = 2 cm, $\widehat{ANI}= {90}^o$.

Xét tam giác ANI vuông tại N, áp dụng định lí Pythagore, ta có

AI² = AN² + IN² = 2² + 2² = 8.

Suy ra $AI = \sqrt{8} = 2\sqrt{2}\left(cm\right)$.

Vì CEIF là hình vuông nên IE = CF = 3 cm, $\widehat{IEC}= {90}^o$.

Xét tam giác IEC vuông tại E, áp dụng định lí Pythagore, ta có

IC² = IE² + EC² = 3² + 3² = 18.

Suy ra $IC = \sqrt{18} = 3\sqrt{2} \left(cm\right)$

Vậy độ dài đường chéo của hai hình vuông AMIN và CEIF  lần lượt là $2\sqrt{2} cm$ và $3\sqrt{2} cm$

b)

Cách 1: Độ dài đường chéo hình vuông là:

AC = AI + IC = $2\sqrt{2} + 3\sqrt{2} = 5\sqrt{2}$

Cách 2:

• Vì BMIE là hình chữ nhật nên BM = IE = 3 cm.

• Vì DNIF là hình chữ nhật nên IN = DF = 2 cm.

Độ dài cạnh AB là: AB = AM + BM = 2 + 3 = 5 (cm).

Độ dài cạnh BC là: BC = BE + EC = 2 + 3 = 5 (cm).

Vì ABCD là hình vuông nên $\widehat{BAC}= {90}^o$ , suy ra tam giác ABC vuông tại B.

Xét tam giác ABC vuông tại B, áp dụng định lí Pythagore, ta có

AC² = AB² + BC² = 5² + 5² = 50.

Suy ra $AC = \sqrt{50} = 5\sqrt{2}$ (cm).

Vậy độ dài đường chéo của hình vuông ABCD là $5\sqrt{2} cm$.

Lời giải bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay, chi tiết khác:

Thực hành 3 trang 55 Toán 9 Tập 1 Chân trời sáng tạo

Giải Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai - Chân trời sáng tạo

Thực hành 3 trang 55 Toán 9 Tập 1: Rút gọn các biểu thức:

Lời giải:

Lời giải bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay, chi tiết khác:

Thực hành 4 trang 56 Toán 9 Tập 1 Chân trời sáng tạo

Giải Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai - Chân trời sáng tạo

Thực hành 4 trang 56 Toán 9 Tập 1: Rút gọn các biểu thức sau:

Lời giải:

Lời giải bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay, chi tiết khác:

Vận dụng 2 trang 56 Toán 9 Tập 1 Chân trời sáng tạo

Giải Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai - Chân trời sáng tạo

Vận dụng 2 trang 56 Toán 9 Tập 1: Trả lời câu hỏi trong Hoạt động khởi động (trang 52).

Một khu đất hình tam giác vuông tiếp giáp hai thửa ruộng hình vuông có diện tích như hình bên. Khu đất hình tam giác vuông có chu vi bằng chu vi thửa ruộng bé không? Kiểm tra bằng cách nào?

Lời giải:

• Hình vuông bé (màu cam) có diện tích là 1 800 m².

Khi đó, cạnh thửa ruộng bé hình vuông là: $\sqrt{1 800}= \sqrt{900. 2}= 30\sqrt{2}$ (m).

Chu vi thửa ruộng bé là: $30\sqrt{2} . 4= 120\sqrt{2}$(m).

• Hình vuông lớn có diện tích (màu vàng) là 3 200 m².

Khi đó, cạnh thửa ruộng lớn hình vuông là: $\sqrt{3 200}= \sqrt{1 600 . 2}= 40\sqrt{2}$.

• Hình tam giác vuông (màu xanh) có hai cạnh góc vuông là hai cạnh của của hai hình vuông trong hình vẽ trên.

Áp dụng định lí Pythagore vào tam giác vuông (màu xanh), ta có:

Độ dài cạnh huyền của tam giác vuông (màu xanh) là:

${\left(30\sqrt{2}\right)}^2 + {\left(40\sqrt{2}\right)}^2 = \sqrt{1 800 + 3 200}$

=$\sqrt{5 000}= \sqrt{2 500. 2}= 50\sqrt{2}$ (m).

Chu vi tam giác vuông là: $30\sqrt{2} + 40\sqrt{2} + 50\sqrt{2} = 120\sqrt{2} \left(m\right)$.

Vậy khu đất hình tam giác vuông có chu vi bằng chu vi thửa ruộng bé.

Lời giải bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay, chi tiết khác:

Bài 1 trang 56 Toán 9 Tập 1 Chân trời sáng tạo

Giải Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai - Chân trời sáng tạo

Bài 1 trang 56 Toán 9 Tập 1: Trục căn thức ở mẫu các biểu thức sau:

Lời giải:

Lời giải bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay, chi tiết khác:

Bài 2 trang 56 Toán 9 Tập 1 Chân trời sáng tạo

Giải Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai - Chân trời sáng tạo

Bài 2 trang 56 Toán 9 Tập 1: Khử mẫu của biểu thức lấy căn:

Lời giải:

Lời giải bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay, chi tiết khác:

Bài 3 trang 56 Toán 9 Tập 1 Chân trời sáng tạo

Giải Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai - Chân trời sáng tạo

Bài 3 trang 56 Toán 9 Tập 1: Trục căn thức ở mẫu các biểu thức sau:

Lời giải:

Lời giải bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay, chi tiết khác:

Bài 4 trang 56 Toán 9 Tập 1 Chân trời sáng tạo

Giải Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai - Chân trời sáng tạo

Bài 4 trang 56 Toán 9 Tập 1: Rút gọn các biểu thức sau:

Lời giải:

Lời giải bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay, chi tiết khác:

Bài 5 trang 56 Toán 9 Tập 1 Chân trời sáng tạo

Giải Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai - Chân trời sáng tạo

Bài 5 trang 56 Toán 9 Tập 1: Tính:

Lời giải:

Lời giải bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay, chi tiết khác:

Bài 6 trang 56 Toán 9 Tập 1 Chân trời sáng tạo

Giải Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai - Chân trời sáng tạo

Bài 6 trang 56 Toán 9 Tập 1: Chứng minh rằng:

Lời giải:

Lời giải bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay, chi tiết khác:

Bài 7 trang 56 Toán 9 Tập 1 Chân trời sáng tạo

Giải Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai - Chân trời sáng tạo

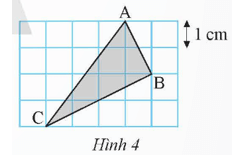
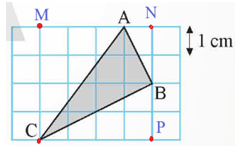
Bài 7 trang 56 Toán 9 Tập 1: Tam giác ABC được vẽ trên lưới ô vuông như Hình 4. Tính diện tích và chu vi của tam giác ABC.

Lời giải:

Gọi các điểm M, N, P như hình vẽ.

Độ dài mỗi cạnh của lưới ô vuông bằng 1 cm.

Hình vuông MNPC chứa tam giác ABC có độ dài mỗi cạnh bằng 4 cm.

Diện tích hình vuông MNPC là: S_MNPC = 4² = 16 (cm²).

• Xét tam giác AMC có AM = 3 cm, CM = 4 cm.

Áp dụng định lí Pythagore, ta có: AC² = AM² + CM² = 3² + 4² = 25.

Suy ra AC = 5 cm.

Diện tích tam giác AMC là: $S_{AMC} = \frac{1}{2}. 3 . 4 = 6 \left(c{m}^2\right)$.

• Xét tam giác ABN có AN = 1 cm, BN = 2 cm.

Áp dụng định lí Pythagore, ta có: AB² = AN² + BN² = 1² + 2² = 5.

Suy ra $AB = \sqrt{5} cm$

Diện tích tam giác ABN là: $S_{ABN }= \frac{1}{2} . 1 . 2 = 1\left(c{m}^2\right)$.

• Xét tam giác BCP có NP = 2 cm, CP = 4 cm.

Áp dụng định lí Pythagore, ta có: BC² = NP² + CP² = 2² + 4² = 20.

Suy ra $BC = \sqrt{20} = 2\sqrt{5} \left(cm\right)$

Diện tích tam giác BCP là: $S_{BCP} = \frac{1}{2}. 2. 4 = 4 \left(c{m}^2\right)$.

Khi đó, chu vi tam giác ABC là: AB + BC + AC = $\sqrt{5} + 2\sqrt{5} +5 = 5 + 3\sqrt{5}$

Diện tích tam giác ABC là:

S_ABC = S_MNPC – S_AMC – S_ABN – S_BCP = 16 – 6 – 1 – 4 = 5 (cm²).

Vậy chu vi tam giác ABC là $5 + 3\sqrt{5} \left(cm\right)$  và diện tích tam giác ABC là 5 cm².

Lời giải bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay, chi tiết khác:

Bài 8 trang 56 Toán 9 Tập 1 Chân trời sáng tạo

Giải Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai - Chân trời sáng tạo

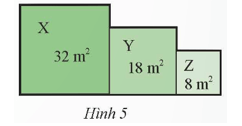
Bài 8 trang 56 Toán 9 Tập 1: Một vườn hoa gồm ba thửa hình vuông X, Y, Z lần lượt có diện tích như Hình 5. Tính chu vi của vườn hoa đó.

Lời giải:

• Cạnh hình vuông X là: $\sqrt{32} = \sqrt{16.2}=4\sqrt{2} \left(m\right)$

Suy ra chu vi hình vuông X là: $4 . 4\sqrt{2}=16\sqrt{2} \left(m\right)$

• Cạnh hình vuông Y là: $\sqrt{18} = \sqrt{9. 2} = 3\sqrt{2} \left(m\right)$

Suy ra chu vi hình vuông Y là: $4. 3\sqrt{2} = 12\sqrt{2}\left(m\right)$

• Cạnh hình vuông Z là: $\sqrt{8} = \sqrt{4 . 2} = 2\sqrt{2}\left(m\right)$

Suy ra chu vi hình vuông Z là: $4. 2\sqrt{2} = 8\sqrt{2}\left(m\right)$

Do đó, chu vi của vườn hoa đó là: $16\sqrt{2} + 12\sqrt{2} + 8\sqrt{2} = 36\sqrt{2} \left(m\right)$

Vậy chu vi của vườn hoa đó là $36\sqrt{2}$m

Lời giải bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay, chi tiết khác: