Bài 1.9 trang 16 Toán 9 Kết nối tri thức Tập 1 | Giải Toán 9
Giải Toán 9 Bài 2: Giải hệ hai phương trình bậc nhất hai ẩn - Kết nối tri thức
Bài 1.9 trang 16 Toán 9 Tập 1: Dùng MTCT thích hợp để tìm nghiệm của các hệ phương trình sau:
a)
b)
c)
d)
Lời giải:
a) Ta đưa hệ phương trình đã cho về dạng .
Ta có a1 = 12, b1 = –5, c1 = –24, a2 = 5, b2 = 3, c2 = –10.
Lần lượt thực hiện các bước sau (với máy tính thích hợp):
Bước 1. Vào chức năng giải hệ hai phương trình bậc nhất hai ẩn bằng cách bấm các phím  (xem màn hình sau bước 1, con trỏ ở vị trí a1).
(xem màn hình sau bước 1, con trỏ ở vị trí a1).

Bước 2. Nhập các số a1 = 12, b1 = –5, c1 = –24, a2 = 5, b2 = 3, c2 = –10 bằng cách bấm:
 (xem màn hình sau bước 2).
(xem màn hình sau bước 2).

Bước 3. Đọc kết quả: Sau khi kết thúc bước 2, bấm  , màn hình cho x = –2 bấm tiếp bàn phím
, màn hình cho x = –2 bấm tiếp bàn phím  ), màn hình cho y = 0 (xem màn hình sau bước 3).
), màn hình cho y = 0 (xem màn hình sau bước 3).

Vậy nghiệm của hệ phương trình đã cho là (–2; 0).
b) Ta có
Lần lượt thực hiện các bước sau (với máy tính thích hợp):
Bước 1. Vào chức năng giải hệ hai phương trình bậc nhất hai ẩn bằng cách bấm các phím  (xem màn hình sau bước 1, con trỏ ở vị trí a1).
(xem màn hình sau bước 1, con trỏ ở vị trí a1).

Bước 2. Nhập các số bằng cách bấm:
 (xem màn hình sau bước 2).
(xem màn hình sau bước 2).

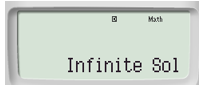
Bước 3. Đọc kết quả: Sau khi kết thúc bước 2, bấm  (xem màn hình sau bước 3).
(xem màn hình sau bước 3).
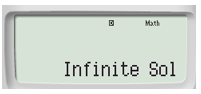
Vậy hệ phương trình đã cho có vô số nghiệm.
c) Ta có
Lần lượt thực hiện các bước sau (với máy tính thích hợp):
Bước 1. Vào chức năng giải hệ hai phương trình bậc nhất hai ẩn bằng cách bấm các phím  (xem màn hình sau bước 1, con trỏ ở vị trí a1).
(xem màn hình sau bước 1, con trỏ ở vị trí a1).

Bước 2. Nhập các số bằng cách bấm:
 (xem màn hình sau bước 2).
(xem màn hình sau bước 2).
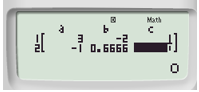
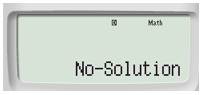
Bước 3. Đọc kết quả: Sau khi kết thúc bước 2, bấm  (xem màn hình sau bước 3).
(xem màn hình sau bước 3).
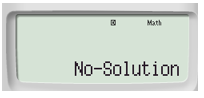
Vậy hệ phương trình đã cho vô nghiệm.
d) Ta có .
Lần lượt thực hiện các bước sau (với máy tính thích hợp):
Bước 1. Vào chức năng giải hệ hai phương trình bậc nhất hai ẩn bằng cách bấm các phím  (xem màn hình sau bước 1, con trỏ ở vị trí a1).
(xem màn hình sau bước 1, con trỏ ở vị trí a1).

Bước 2. Nhập các số bằng cách bấm:
 (xem màn hình sau bước 2).
(xem màn hình sau bước 2).

Bước 3. Đọc kết quả: Sau khi kết thúc bước 2, bấm  , màn hình cho bấm tiếp bàn phím
, màn hình cho bấm tiếp bàn phím  ), màn hình cho y = –15 (xem màn hình sau bước 3).
), màn hình cho y = –15 (xem màn hình sau bước 3).

Vậy nghiệm của hệ phương trình đã cho là .
Lời giải bài tập Toán 9 Bài 2: Giải hệ hai phương trình bậc nhất hai ẩn hay, chi tiết khác:
 (xem màn hình sau bước 1, con trỏ ở vị trí a1).
(xem màn hình sau bước 1, con trỏ ở vị trí a1).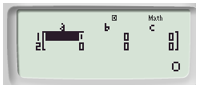


 (xem màn hình sau bước 1, con trỏ ở vị trí a1).
(xem màn hình sau bước 1, con trỏ ở vị trí a1).



 (xem màn hình sau bước 1, con trỏ ở vị trí a1).
(xem màn hình sau bước 1, con trỏ ở vị trí a1).


 (xem màn hình sau bước 2).
(xem màn hình sau bước 2).

 (xem màn hình sau bước 2).
(xem màn hình sau bước 2).
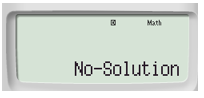
 (xem màn hình sau bước 2).
(xem màn hình sau bước 2).
