Giải Toán 9 | No tags
Với giải bài tập Toán 9 Bài 30: Đa giác đều sách Kết nối tri thức hay nhất, chi tiết giúp học sinh lớp 9 dễ dàng làm bài tập Toán 9 Bài 30.
Video Giải Toán 9 Bài 30: Đa giác đều - Cô Ngô Vân (Giáo viên VietJack)
1. Đa giác đều
HĐ1 trang 84 Toán 9 Tập 2: Ta đã biết các tam giác đều và hình vuông có các đỉnh nằm trên một đường tròn. Ta dựng một đa giác lồi 5 cạnh có các đỉnh nằm trên một đường tròn như sau:
– Vẽ đường tròn tâm O bán kính R.
– Lần lượt lấy các điểm A, B, C, D, E trên đường tròn theo thứ tự ngược chiều kim đồng hồ (hoặc theo chiều kim đồng hồ) sao cho:
Em hãy giải thích vì sao các cạnh và các góc của đa giác ABCDE bằng nhau (H.9.39).
Lời giải:
Vì năm điểm A, B, C, D, E cùng nằm trên đường tròn (O) nên OA = OB = OC = OD = OE.
Xét ∆AOB và ∆BOC có:
OA = OB, OB = OC
Do đó ∆AOB = ∆BOC (c.g.c)
Tương tự, ta sẽ chứng minh được: ∆AOB = ∆BOC = ∆COD = ∆DOE = ∆EOA.
Do đó:
⦁ AB = BC = CD = DE = EA;
⦁
⦁
Suy ra
Hay
Vậy các cạnh và các góc của đa giác ABCDE bằng nhau.
Lời giải bài tập Toán 9 Bài 30: Đa giác đều hay, chi tiết khác:
Câu hỏi trang 85 Toán 9 Tập 2: Nếu một lục giác đều (đa giác đều 6 cạnh) nội tiếp đường tròn bán kính 2 cm (H.9.40) thì độ dài các cạnh của lục giác đều bằng bao nhiêu centimét? Số đo các góc của lục giác đều bằng bao nhiêu độ?
Lời giải:
Vì ABCDEF là lục giác đều nên AB = BC = CD = DE = EF = FA.
Vì lục giác đều ABCDEF nội tiếp đường tròn (O) nên OA = OB = OC = OD = OE = OF.
Xét ∆AOB và ∆BOC có:
OA = OB, OB = OC, AB = BC.
Do đó ∆AOB = ∆BOC (c.c.c)
Tương tự, ta sẽ chứng minh được:
∆AOB = ∆BOC = ∆COD = ∆DOE = ∆EOF = ∆OFA.
Do đó:
Mà
Suy ra nên
Xét ∆OAB có OA = OB nên ∆OAB cân tại O, lại có nên ∆OAB là tam giác đều. Suy ra AB = OA = OB = 2 cm và
Tương tự, ta chứng minh được ∆OAF là tam giác đều nên
Khi đó hay
Do đó, vì ABCDEF là lục giác đều nên các góc bằng nhau và bằng 120°.
Vậy độ dài các cạnh của lục giác đều bằng 2 centimét và số đo các góc của lục giác đều bằng 120°.
Lời giải bài tập Toán 9 Bài 30: Đa giác đều hay, chi tiết khác:
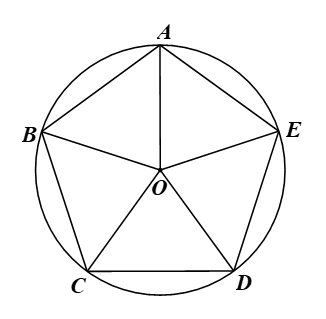
Luyện tập 1 trang 86 Toán 9 Tập 2: Cho M, N, P, Q, K lần lượt là trung điểm của các cạnh AB, BC, CD, DE và EA của ngũ giác đều ABCDE (H.9.44). Hỏi MNPQK có phải là ngũ giác đều hay không?
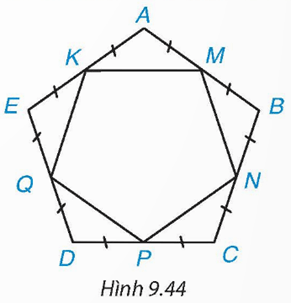
Lời giải:
⦁ Vì ABCDE là ngũ giác đều nên AB = BC = CD = DE = EA (1) và
Vì M, N, P, Q, K lần lượt là trung điểm của các cạnh AB, BC, CD, DE và EA nên
Từ (1) và (2) suy ra MA = MB = NB = NC = PC = PD = QD = QE = KE = KA.
Xét ∆AKM và ∆BMN có:
AK = BM, AM = BN
Do đó ∆AKM = ∆BMN (c.g.c)
Suy ra KM = MN (hai cạnh tương ứng) và (hai góc tương ứng). (3)
Tương tự, sẽ ta chứng minh được:
∆AKM = ∆BMN = ∆CNP = ∆DPQ = ∆EQK.
Suy ra KM = MN = NP = PQ = QK. (8)
⦁ Xét ∆AKM có AK = AM nên ∆AKM cân tại A, suy ra
Từ (3) và (4) suy ra
Chứng minh tương tự như trên ta có:
Ta có
Suy ra nên
Tương tự, ta chứng minh được:
Từ (5), (6) và (7) suy ra
Từ (8) và (9) suy ra MNPQK có các cạnh bằng nhau và các góc bằng nhau.
Vậy MNPQK là ngũ giác đều.
Lời giải bài tập Toán 9 Bài 30: Đa giác đều hay, chi tiết khác:
Thử thách nhỏ 1 trang 87 Toán 9 Tập 2: Cho một bát giác đều (đa giác đều 8 cạnh) nội tiếp một đường tròn tâm O (H.9.45). Hỏi mỗi góc của bát giác đều có số đo bằng bao nhiêu?
Lời giải:
:
Giả sử ABCDEGHK là bát giác đều nội tiếp đường tròn (O).
Do đó AB = BC = CD = DE = EG = GH = HK và OA = OB = OC = OD = OE = OG = OH = OK.
Xét ∆OAB và ∆OBC có:
OA = OB, OB = OC, AB = BC
Do đó ∆OAB = ∆OBC (c.c.c).
Tương tự, ta sẽ chứng minh được:
∆OAB = ∆OBC = ∆COD = ∆DOE = ∆EOG = ∆GOH = ∆HOK = ∆KOA.
Suy ra các góc tương ứng bằng nhau:
Ta có:
Suy ra nên
Lại có (tổng ba góc của ∆OAB bằng 180°)
Suy ra
Vì ∆AOB = ∆OKA nên (hai góc tương ứng).
Suy ra
Do đó, vì ABCDEGHK là bát giác đều nên các góc bằng nhau và bằng 135°.
Bát giác đều ABCDEGHK được chia thành ba tứ giác ABCD, ADEG và AGHG.
Ta thấy tổng số đo các góc của bát giác ABCDEGHK bằng tổng số đo các góc của ba tứ giác kể trên.
Mà mỗi tứ giác có tổng số đo các góc bằng 360°, do đó tổng số đo các góc của bát giác đều ABCDEGHK là: 3.360° = 1 080°.
Vì ABCDEGHK là bát giác đều nên 8 góc của bát giác bằng nhau và mỗi góc có số đo bằng
Vậy mỗi góc của bát giác đều có số đo bằng 135°.
Lời giải bài tập Toán 9 Bài 30: Đa giác đều hay, chi tiết khác:
HĐ2 trang 87 Toán 9 Tập 2: Để bày bàn ăn cho nhiều người, các nhà hàng thường sử dụng bàn xoay có dạng hình tròn và quay được quanh tâm của hình tròn. Đặt một chiếc cốc nhỏ ở vị trí điểm A trên bàn xoay có dạng hình tròn với tâm O sao cho điểm A khác điểm O. Khi quay bàn xoay thuận chiều quay của kim đồng hồ (H.9.46) thì chiếc cốc di chuyển đến một vị trí mới là điểm B.
Em hãy so sánh khoảng cách từ hai điểm A và B đến điểm O. Hai điểm A, B có cùng nằm trên một đường tròn tâm O hay không?
Lời giải:
Khi quay bàn xoay thì khoảng cách từ tâm O đến chiếc cốc không thay đổi nên OA = OB. Do đó khoảng cách từ hai điểm A và B đến điểm O bằng nhau.
Vì OA = OB nên hai điểm A, B cùng nằm trên đường tròn tâm O.
Lời giải bài tập Toán 9 Bài 30: Đa giác đều hay, chi tiết khác:
HĐ3 trang 87 Toán 9 Tập 2: Trên bàn xoay tâm O, vẽ tam giác đều ABC nội tiếp một đường tròn (O) và hai tia OA, OB (H.9.47). Khi quay bàn xoay thuận chiều quay của kim đồng hồ để tia OA di chuyển trùng với tia OB (ở vị trí ban đầu), điểm A có di chuyển đến vị trí của điểm B không và sẽ di chuyển trên cung tròn nào của đường tròn (O)? Khi đó, điểm C sẽ di chuyển đến vị trí của điểm nào?
Lời giải:
Vì tam giác ABC đều nên AB = BC = CA.
Vì tam giác ABC nội tiếp đường tròn (O) nên OA = OB = OC.
Xét ∆OAB và ∆OBC có:
OA = OB, OB = OC, AB = BC
Do đó ∆OAB = ∆OBC (c.c.c)
Suy ra (hai góc tương ứng).
Vì vậy, nếu quay bàn xoay thuận chiều quay của kim đồng hồ để tia OA di chuyển trùng với tia OB (ở vị trí ban đầu), điểm A di chuyển đến vị trí của điểm B và sẽ di chuyển trên cung tròn AB của đường tròn (O).
Khi đó, tia OB di chuyển trùng với tia OC (ở vị trí ban đầu), tia OC di chuyển trùng với tia OA (ở vị trí ban đầu). Vậy điểm C sẽ di chuyển đến vị trí của điểm A.
Lời giải bài tập Toán 9 Bài 30: Đa giác đều hay, chi tiết khác:
Câu hỏi trang 88 Toán 9 Tập 2:
a) Phép quay ngược chiều 180° tâm O biến điểm A thành điểm A’. Hỏi điểm A’ có đối xứng với điểm A qua O hay không?
b) Nếu phép quay thuận chiều α° tâm O biến điểm A thành điểm B thì phép quay ngược chiều α° tâm O có biến điểm B thành điểm A hay không?
Lời giải:
a) Phép quay ngược chiều 180° tâm O biến điểm A thành điểm A’.
Khi đó A’ thuộc đường tròn (O; OA) sao cho tia OA quay ngược chiều kim đồng hồ đến tia OA’, điểm A tạo nên cung AA’ có số đo 180°.
Suy ra OA’ = OA và hay ba điểm A, O, A’ thẳng hàng.
Vậy O là trung điểm của AA’ hay điểm A’ có đối xứng với điểm A qua O.
b) Phép quay thuận chiều α° tâm O biến điểm A thành điểm B.
Khi đó điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB, điểm A tạo nên cung AB có số đo α°.
Suy ra OB = OA và
Do đó điểm A thuộc đường tròn (O; OB) và tia OB quay ngược chiều kim đồng hồ đến tia OA, điểm B tạo nên cung BA có số đo α°.
Vậy phép quay ngược chiều α° tâm O có biến điểm B thành điểm A.
Lời giải bài tập Toán 9 Bài 30: Đa giác đều hay, chi tiết khác:
Luyện tập 2 trang 88 Toán 9 Tập 2: Cho hình vuông ABCD nội tiếp đường tròn (O) như Hình 9.50.
a) Phép quay thuận chiều 90° tâm O biến các điểm A, B, C, D thành những điểm nào? Phép quay này có giữ nguyên hình vuông ABCD không?
b) Hãy liệt kê thêm ba phép quay khác với tâm O theo chiều kim đồng hồ giữ nguyên hình vuông ABCD.
Lời giải:
a) Phép quay thuận chiều 90° với tâm O biến các điểm A, B, C, D thành các điểm tương ứng là B, C, D, A.
Phép quay này giữ nguyên hình vuông ABCD.
b) Ta có ba phép quay tâm O theo chiều kim đồng hồ giữ nguyên hình vuông ABCD:
⦁ Phép quay thuận chiều 180° tâm O;
⦁ Phép quay thuận chiều 270° tâm O;
⦁ Phép quay thuận chiều 360° tâm O.
Lời giải bài tập Toán 9 Bài 30: Đa giác đều hay, chi tiết khác:
Thực hành trang 88 Toán 9 Tập 2: Cho điểm O và điểm A khác điểm O (H.9.51).
Phép quay ngược chiều 60° tâm O biến điểm A thành điểm A’: Xác định điểm A’ theo hướng dẫn sau: Vẽ đường tròn (O; OA) và tia Ox sao cho tia Ox cắt đường tròn (O; OA) tại điểm A’ (H.9.51).
Lời giải:
HS thực hiện theo hướng dẫn của GV và SGK.
Lời giải bài tập Toán 9 Bài 30: Đa giác đều hay, chi tiết khác:
Thử thách nhỏ 2 trang 89 Toán 9 Tập 2: Hãy liệt kê 6 phép quay giữ nguyên một lục giác đều nội tiếp một đường tròn (O).
Lời giải:
Giả sử lục giác đều ABCDEF nội tiếp đường tròn (O) (hình vẽ).
Vì lục giác ABCDEF nội tiếp đường tròn (O) nên OA = OB = OC = OD = OE = OF.
Vì ABCDEF là lục giác đều nên AB = BC = CD = DE = EF = FA.
Xét ∆OAB và ∆OBC có:
OA = OB, OB = OC, AB = BC.
Do đó ∆OAB = ∆OBC (c.c.c).
Chứng minh tương tự ta có
∆OAB = ∆OBC = ∆COD = ∆DOE = ∆EOF = ∆FOA.
Suy ra
Mà
Do đó
Suy ra
Khi đó phép quay ngược chiều 72° tâm O giữ nguyên điểm O, biến điểm A thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay ngược chiều kim đồng hồ đến tia OB, điểm A tạo nên cung AB có số đo 60°.
Vậy mỗi phép quay thuận chiều 60° tâm O ở mỗi đỉnh A, B, C, D, E, F sẽ giữ nguyên lục giác đều nội tiếp đường tròn tâm O.
Lời giải bài tập Toán 9 Bài 30: Đa giác đều hay, chi tiết khác:
Bài 9.24 trang 89 Toán 9 Tập 2: Trong các hình phẳng sau (H.9.52), hình nào là hình phẳng có dạng đa giác đều?
Lời giải:
Hình b là hình vuông, hình d là hình lục giác đều vì hai hình đều có các cạnh bằng nhau và các góc bằng nhau.
Lời giải bài tập Toán 9 Bài 30: Đa giác đều hay, chi tiết khác:
Bài 9.25 trang 89 Toán 9 Tập 2: Trong các hình dưới đây (H.9.53), hình nào vẽ hai điểm M và N thỏa mãn phép quay thuận chiều 60° tâm O biến điểm M thành điểm N?
Lời giải:
Phép quay thuận chiều 60° tâm O biến điểm M thành điểm N tức là điểm N thuộc đường tròn (O; OM) sao cho tia OM quay thuận kim đồng hồ đến tia ON và điểm M tạo nên cung MN có số đo là 60°.
Trong các hình đã cho, hình d là hình cần tìm.
Lời giải bài tập Toán 9 Bài 30: Đa giác đều hay, chi tiết khác:
Bài 9.26 trang 89 Toán 9 Tập 2: Cho tam giác đều ABC nội tiếp đường tròn (O) bán kính 2 cm. Tính độ dài các cạnh của tam giác ABC.
Lời giải:
Vì tam giác đều ABC nội tiếp đường tròn (O) bán kính 2 cm nên ta có OA = OB = OC = 2 cm.
Vì ABC là tam giác đều nên tâm O của đường tròn ngoại tiếp tam giác là trọng tâm của tam giác.
Gọi H là giao điểm của AO và BC. Khi đó AH vừa là đường trung trực, vừa đường cao, vừa là đường trung tuyến của tam giác.
Do đó suy ra
Vì ∆ABC đều nên
Xét ∆ABH vuông tại H, ta có:
Vì AH là đường trung tuyến của ∆ABC nên H là trung điểm của BC, do đó BC = 2BH = 2 (cm)
Vậy các cạnh của tam giác ABC có độ dài bằng 2 cm.
Lời giải bài tập Toán 9 Bài 30: Đa giác đều hay, chi tiết khác:
Bài 9.27 trang 89 Toán 9 Tập 2: Cho hình thoi ABCD có Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng MBNPDQ là lục giác đều.
Lời giải:
⦁ Vì ABCD là hình thoi nên AB = BC = CD = DA.
Vì M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA nên MA = MB = AB; NB = NC = BC; PC = PD = CD; QD = QA = DA.
Do đó AM = MB = NB = NC = PC = PD = QD = QA = AB. (1)
Xét ∆ABD có AB = AD nên ∆ABD cân tại A, lại có nên ∆ABD là tam giác đều. Do đó AB = BD (2) và
Lại có M, Q là lần lượt là trung điểm của AB, AD nên MQ là đường trung bình của tam giác. Do đó MQ // BD và MQ = BD. (3)
Chứng minh tương tự, ta cũng có NP = BD. (4)
Từ (1), (2), (3) và (4) suy ra MB = BN = NP = PD = DQ = QM.
⦁ Vì MQ // BD nên (so le trong).
Mà (hai góc kề bù)
Suy ra
Tương tự, ta có
Tam giác BCD có BC = CD và (tính chất hình thoi) nên ∆BCD là tam giác đều. Do đó
Ta có
Khi đó,
Như vậy MBNPDQ có các cạnh bằng nhau và các góc bằng nhau.
Vậy MBNPDQ là lục giác đều.
Lời giải bài tập Toán 9 Bài 30: Đa giác đều hay, chi tiết khác:
Bài 9.28 trang 89 Toán 9 Tập 2: Cho tam giác đều ABC nội tiếp đường tròn (O) như Hình 9.54. Phép quay ngược chiều 60° tâm O biến các điểm A, B, C lần lượt thành các điểm D, E, F. Chứng minh rằng ADBECF là một lục giác đều.
Lời giải:
⦁ Vì ∆ABC là tam giác đều nên
Xét đường tròn (O) có lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung AB nên suy ra
⦁ Vì phép quay ngược chiều 60° tâm O biến điểm A thành các điểm D nên điểm D nằm trên đường tròn (O; OA) sao cho tia OA quay ngược chiều kim đồng hồ đến tia OD thì điểm A tạo nên cung AD có số đo 60°.
Khi đó ta có OA = OD và nên ∆OAD là tam giác đều.
Suy ra AD = OA = OD và
⦁ Mặt khác, (hai góc kề nhau)
Nên
Xét ∆BOD có OB = OD (cùng bằng OA) và nên ∆BOD là tam giác đều.
Do đó BD = OB = OD và
Từ (1) và (2) ta có AD = DB và
Tương tự, ta sẽ chứng minh được:
AD = DB = BE = EC = CF = FA và
Vậy ADBECF có các cạnh bằng nhau và các góc đều bằng 120° nên là một lục giác đều.
Lời giải bài tập Toán 9 Bài 30: Đa giác đều hay, chi tiết khác:
Bài 9.29 trang 89 Toán 9 Tập 2: Liệt kê năm phép quay giữ nguyên một ngũ giác đều nội tiếp một đường tròn tâm O.
Lời giải:
Giả sử ABCDE là ngũ giác đều nội tiếp đường tròn (O) (hình vẽ).
Vì ngũ giác ABCDE nội tiếp đường tròn (O) nên OA = OB = OC = OD = OE.
Vì ABCDE là ngũ giác đều nên AB = BC = CD = DE = EA.
Xét ∆OAB và ∆OBC có:
OA = OB, OB = OC, AB = BC.
Do đó ∆OAB = ∆OBC (c.c.c).
Chứng minh tương tự ta có
∆OAB = ∆OBC = ∆COD = ∆DOE = ∆EOA.
Suy ra
Mà
Do đó
Suy ra
Khi đó phép quay ngược chiều 72° tâm O giữ nguyên điểm O, biến điểm A thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay ngược chiều kim đồng hồ đến tia OB, điểm A tạo nên cung AB có số đo 72°.
Vậy mỗi phép quay ngược chiều 72° tâm O ở mỗi đỉnh A, B, C, D, E sẽ giữ nguyên ngũ giác đều nội tiếp một đường tròn tâm O.
Lời giải bài tập Toán 9 Bài 30: Đa giác đều hay, chi tiết khác:
Bài 9.30 trang 89 Toán 9 Tập 2: Cho vòng quay mặt trời gồm tám cabin như Hình 9.55. Hỏi để cabin A di chuyển đến vị trí cao nhất thì vòng quay phải quay thuận chiều quay của kim đồng hồ quanh tâm bao nhiêu độ?
Lời giải:
Giả sử 8 cabin tạo thành một bát giác đều ABCDEGHK nội tiếp đường tròn (O) (hình vẽ).
Vì bát giác ABCDEGHK nội tiếp đường tròn (O) nên OA = OB = OC = OD = OE = OG = OH = OK.
Vì ABCDEGHK là ngũ giác đều nên AB = BC = CD = DE = EG = GH = HK = KA.
Xét ∆OAB và ∆OBC có:
OA = OB, OB = OC, AB = BC.
Do đó ∆OAB = ∆OBC (c.c.c).
Chứng minh tương tự ta có
∆OAB = ∆OBC = ∆COD = ∆DOE = ∆EOG = ∆GOH = ∆HOK = ∆KOA.
Suy ra
Mà
Do đó
Suy ra
Khi đó
Để cabin A di chuyển đến vị trí cao nhất (vị trí của cabin G ban đầu) thì tia OA quay thuận chiều kim đồng hồ đến tia OG, điểm A tạo nên cung AG có số đo 135°.
Vậy để cabin A di chuyển đến vị trí cao nhất thì vòng quay phải quay thuận chiều kim đồng hồ quanh tâm có số đo là 135°.
Lời giải bài tập Toán 9 Bài 30: Đa giác đều hay, chi tiết khác: