Lũy thừa với số mũ tự nhiên (Lý thuyết Toán lớp 6) | Chân trời sáng tạo
Với tóm tắt lý thuyết Toán lớp 6 Bài 4: Lũy thừa với số mũ tự nhiên hay nhất, chi tiết sách Chân trời sáng tạo
sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 6.
Lũy thừa với số mũ tự nhiên (Lý thuyết Toán lớp 6) | Chân trời sáng tạo
Lý thuyết Lũy thừa với số mũ tự nhiên
1. Lũy thừa
Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a.
an = a . a ….. a (n thừa số a) (n )
Ta đọc an là “a mũ n” hoặc “lũy thừa bậc n của”.
Số a được gọi là cơ số, n được gọi là số mũ.
Ví dụ: 85 đọc là “tám mũ năm”, có cơ số là 8 và số mũ là 5.
Phép nhân nhiều thừa số giống nhau như trên được gọi là phép nâng lên lũy thừa.
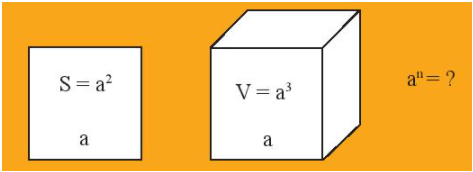
Đặc biệt, a2 còn được đọc là “a bình phương” hay “bình phương của a”.
a3 được đọc là “a lập phương” hay “lập phương của a”.
Quy ước: a1 = a.
Ví dụ:
a) Tính 23 và 103.
b) Viết 10 000 000 dưới dạng lũy thừa của 10.
c) Viết 16 dưới dạng lũy thừa cơ số 4
Hướng dẫn giải
a) Số 23 là lũy thừa bậc 3 của 2 và là tích của 3 thừa số 2 nhân với nhau nên ta có:
23 = 2 . 2 . 2 = 8.
Số 103 là lũy thừa bậc 3 của 10 và là tích của 3 thừa số 10 nhân với nhau nên ta có:
103 = 10 . 10 . 10 = 1 000.
b) Số 10 000 000 được viết dưới dạng lũy thừa của 10 là:
10 000 000 = 10 . 10 . 10 . 10 . 10 . 10 . 10 = 107.
c) Số 16 được viết dưới dạng lũy thừa cơ số 4 là:
16 = 4 . 4 = 42.
2. Nhân hai lũy thừa cùng cơ số
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ.
am . an = am + n.
Ví dụ:
a) 3 . 35 = 31 . 35 = 31 + 5 = 36
b) 52 . 54 = 52 + 4 = 56
c) a3 . a5 = a3 + 5 = a8.
3. Chia hai lũy thừa cùng cơ số
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ.
am : an = am – n (a ≠ 0; m ≥ n ≥ 0).
Quy ước: a0 = 1 (a ≠ 0).
Ví dụ:
a) a6 : a2 = a6 − 2 = a4 (a ≠ 0)
b) 23 : 23 = 23 − 3 = 20 = 1
c) 81 : 32 = 34 : 32 = 34 − 2 = 32 = 3 . 3 = 9.
Bài tập Lũy thừa với số mũ tự nhiên
Bài 1. Viết kết quả mỗi phép tính sau dưới dạng một lũy thừa.
a) x . x8 ;
b) 42 . 64;
c) 10 . 2 . 5.
Hướng dẫn giải
a) x . x8 = x1 . x8 = x1 + 8 = x9 ;
b) 42 . 64 = 42 . 4 . 4 . 4 = 42 . 43 = 42 + 3 = 45 ;
c) 10 . 2 . 5 = 10 . (2 . 5) = 10 . 10 = 102.
Bài 2. Tính 44 . 4 : 16 + 6.
Hướng dẫn giải
44 . 4 : 16 + 6
= 44 . 41 : 42 + 6
= 44 + 1 – 2 + 6
= 43 + 6
= 4 . 4 . 4 + 6
= 64 + 6 = 70.
Bài 3. Tìm x biết: (2x + 1)3 = 729.
Hướng dẫn giải
(2x + 1)3 = 729
(2x + 1)3 = 93
(2x + 1) = 9
2x + 1 = 9
2x = 9 – 1
2x = 8
x = 4.
Vậy x = 4.
Học tốt Lũy thừa với số mũ tự nhiên
Các bài học để học tốt Lũy thừa với số mũ tự nhiên Toán lớp 6 hay khác:
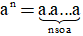
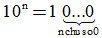
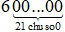 tấn, khối lượng mặt trăng khoảng
tấn, khối lượng mặt trăng khoảng 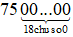 tấn.
tấn.