Tổng hợp lý thuyết Toán lớp 6 Chương 6 Chân trời sáng tạo
Với tóm tắt lý thuyết Toán lớp 6 Ôn tập chương 6 hay nhất, chi tiết sách Chân trời sáng tạo
sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 6.
Tổng hợp lý thuyết Toán lớp 6 Chương 6 Chân trời sáng tạo
Tổng hợp lý thuyết Toán lớp 6 Chương 6
1. Số thập phân âm
- Phân số thập phân là phân số có mẫu số là lũy thừa của 10.
- Các phân số thập phân dương được viết dưới dạng số thập phân dương.
- Các phân số thập phân âm được viết dưới dạng số thập phân âm.
Số thập phân gồm hai phần:
- Phần số nguyên viết bên trái dấu phẩy;
- Phần thập phân viết bên phải dấu phẩy.
2. Số đối của một số thập phân
Hai số thập phân gọi là đối nhau khi chúng biểu diễn hai phân số thập phân đối nhau.
3. So sánh hai số thập phân
- Nếu hai số thập phân trái dấu, số thập phân dương lớn hơn số thập phân âm.
- Trong hai số thập phân âm, số nào có số đối lớn hơn thì số đó nhỏ hơn.
4. Cộng, trừ hai số thập phân
Để thực hiện các phép tính cộng và trừ các số thập phân, ta áp dụng các quy tắc về dấu như khi thực hiện các phép tính cộng và trừ các số nguyên.
- Muốn cộng hai số thập phân âm, ta cộng hai số đối của chúng rồi thêm dấu trừ đằng trước kết quả.
- Muốn cộng hai số thập phân trái dấu, ta làm như sau:
• Nếu số dương lớn hơn hay bằng số đối của số âm thì ta lấy số dương trừ đi số đối của số âm.
• Nếu số dương nhỏ hơn số đối của số âm thì ta lấy số đối của số âm trừ đi số dương rồi thêm dấu trừ (−) trước kết quả.
- Muốn trừ số thập phân a cho số thập phân b, ta cộng a với số đối của b.
Nhận xét:
- Tổng của hai số thập phân cùng dấu luôn cùng dấu với hai số thập phân đó.
- Khi cộng hai số thập phân trái dấu:
• Nếu số dương lớn hơn số đối của số âm thì ta có tổng dương.
• Nếu số dương nhỏ hơn số đối của số âm thì ta có tổng âm.
5. Nhân, chia hai số thập phân dương
Muốn nhân hai số thập phân dương có nhiều chữ số thập phân, ta làm như sau:
- Bỏ dấu phẩy rồi nhân như nhân hai số tự nhiên.
- Đếm xem trong phần thập phân ở cả hai thừa số có tất cả bao nhiêu chữ số rồi dùng dấu phẩy tách ở tích ra bấy nhiêu chữ số từ phải sang trái.
Muốn chia hai số thập phân dương có nhiều chữ số thập phân, ta làm như sau:
- Đếm xem có bao nhiêu chữ số ở phần thập phân của số chia thì chuyển dấu phẩy ở số bị chia sang bên phải bấy nhiêu chữ số.
Chú ý: Khi chuyển dấu phẩy ở số bị chia snag phải mà không đủ chữ số, ta thấy thiếu bao nhiêu chữ số thì thêm vào đó bấy nhiêu chữ số 0.
- Bỏ dấu phẩy ở số chia rồi thực hiện phép chia như chia số thập phân cho số tự nhiên.
6. Nhân, chia hai số thập phân có dấu bất kì
Để thực hiện các phép tính nhân và chia số thập phân, ta áp dụng các quy tắc về dấu như đối với số nguyên để đưa về bài toán nhân hoặc chia hai số thập phân dương với lưu ý sau:
- Tích và thương của hai số thập phân cùng dấu luôn là một số dương.
- Tích và thương của hai số thập phân khác dấu luôn là một số âm.
- Khi nhân hoặc chia hai số thập phân cùng âm, ta nhân hoặc chia hai số đối của chúng.
- Khi nhân hoặc chia hai số thập phân khác dấu, ta chỉ thực hiện phép nhân hoặc phép chia giữa số dương và số đối của số âm rồi thêm dấu trừ (−) trước kết quả nhận được.
7. Tính chất của các phép tính với số thập phân
Phép tính với số thập phân âm có đầy đủ các tính chất giống như các phép tính với số nguyên và phân số:
- Tính chất giao hoán và tính chất kết hợp của phép cộng.
- Tính chất giao hoán và tính chất kết hợp của phép nhân.
- Tính chất phân phối của phép nhân đối với phép cộng.
Quy tắc dấu ngoặc:
- Khi bỏ dấu ngoặc có dấu (+) đứng trước thì dấu các số hạng trong ngoặc vẫn giữ nguyên; khi bỏ dấu ngoặc có dấu (−) đứng trước, ta phải đổi dấu tất cả các số hạng trong dấu ngoặc.
- Khi đưa nhiều số hạng vào trong dấu ngoặc và để dấu (−) đứng trước thì ta phải đổi dấu của tất cả các số hạng đó.
8. Làm tròn số thập phân
Quy tắc làm tròn số thập phân:
Khi làm tròn các số thập phân đến hang nào thì hang đó gọi là hàng quy tròn.
Muốn làm tròn một số thập phân đến một hang quy tròn nào đó, ta thực hiện các bước sau:
- Gạch dưới chữ số thập phân của hàng quy tròn .
- Nhìn sang chữ số ngay bên phải.
• Nếu chữ số đó lớn hơn hoặc bằng 5 thì tang chữ số gạch dưới lên một đơn vị rồi thay tất các chữ số bên phải bằng số 0 hoặc bỏ đi nếu chúng ở phần thập phân.
• Nếu chữ số đó nhỏ hơn 5 thì giữ nguyên chữ số gạch dưới và thay tất các chữ số bên phải bằng số 0 hoặc bỏ đi nếu chúng ở phần thập phân.
9. Ước lượng kết quả
Ta có thể sử dụng quy ước làm tròn số để ước lượng kết quả các phép tính. Nhờ đó có thể dễ dàng phát hiện ra những đáp số không hợp lí.
10. Tỉ số của hai đại lượng
Ta gọi thương trong phép chia số a cho số b (b ≠0) là tỉ số của a và b.
Tỉ số của a và b kí hiệu là a : b (cũng kí hiệu là 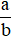 ).
).
Chú ý:
- Phân số 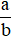 thì cả a và b phải là các số nguyên.
thì cả a và b phải là các số nguyên.
- Tỉ số 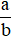 thì a và b có thể là các số nguyên, phân số, hỗn số, số thập phân,…
thì a và b có thể là các số nguyên, phân số, hỗn số, số thập phân,…
- Ta thường dùng khái niệm tỉ số nói về thương của hai đại lượng cùng loại và cùng đơn vị đo.
11. Tỉ số phần trăm của hai đại lượng
Trong thực hành, ta thường dùng tỉ số dưới dạng tỉ số phần trăm với kí hiệu % thay cho 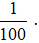 .
.
Để tính tỉ số phần trăm của hai số a và b, ta nhân a với 100 rồi chia cho b và viết kí hiệu % vào bên phải kết quả tìm được.
12. Tìm giá trị phần trăm của một số
Muốn tìm giá trị a% của số b, ta tính: 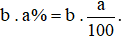 .
.
13. Tìm một số khi biết giá trị phần trăm của số đó
Muốn tìm số b khi biết a% của b là c, ta tính: 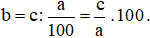 .
.
Bài tập tổng hợp Toán lớp 6 Chương 6
Bài 1. Viết các phân số sau dưới dạng số thập phân:
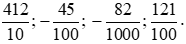
Lời giải:
Các phân số trên đều là phân số thập phân.
Cách đổi các phân số thập phân sang số thập phân thì ta quy về bài toán chia một số cho 10; 100; 1 000 (kết quả để dưới dạng số thập phân).
Quy tắc: Muốn chia một số cho 10; 100; 1 000 ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba, … chữ số.
Đổi lần lượt các phân số thập phân trên ra số thập phân, ta được:
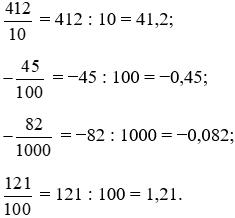
Bài 2. Viết các số thập phân sau đây dưới dạng phân số thập phân:
−14,5; 25,12; −32,46; −0,785.
Lời giải:
- Các phân số thập phân được viết dưới dạng số thập phân.
- Số các chữ số thập phân bằng đúng số các chữ số 0 ở mẫu của phân số thập phân.
Đổi lần lượt các số thập phân trên ra phân số thập phân, ta được:
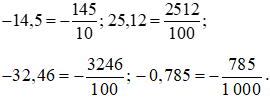
Bài 3. Tìm số đối của các số thập phân sau:
34,18; −26,8; −0,465; 2,4.
Lời giải:
Cách tìm số đối của một số thập phân: ta thêm dấu trừ vào trước số thập phân đó.
Số đối của 34,18 là −34,18;
Số đối của −26,8 là −(−26,8) hay 26,8;
Số đối của −0,465 là −(−0,465) = 0,465;
Số đối của 2,4 là −2,4.
Bài 4: Hãy sắp xếp các số sau theo thứ tự giảm dần:
0,6; −24,45; −24,15; 35,18; 21,75.
Lời giải:
Để sắp xếp các số thập phân sau theo thứ tự giảm dần, ta làm như sau:
Bước 1: Chia thành 2 nhóm số thập dương và số thập phân âm, vì số thập phân âm luôn nhỏ hơn số thập phân dương.
Bước 2: Ta so sánh các số thập phân theo nhóm với nhau:
- Nhóm các số thập phân dương: ta so sánh phần nguyên với nhau, số nào có phần nguyên lớn hơn thì lớn hơn. Nếu phần nguyên bằng nhau thì ta lần lượt so sánh các hàng ở phần thập phân.
- Nhóm các số thập phân âm: ta so sánh số đối của chúng, số nào có số đối lớn hơn thì nhỏ hơn.
Sắp xếp các số thập phân sau theo thứ tự giảm dần:
* Phân loại:
- Nhóm các số thập phân dương: 0,6; 35,18; 21,75.
- Nhóm các số thập phân âm: −24,45; −24,15.
* So sánh các số thập phân trong theo nhóm:
- Nhóm các số thập phân dương: ta so sánh phần nguyên của các số trên.
Vì 35 > 21 > 0 nên 35,18 > 21,75 > 0,6.
- Nhóm các số thập phân âm: Số đối của các số −24,45; −24,15 lần lượt là 24,45; 24,15.
+ Phần nguyên của hai số 24,45; 24,15 đều là 24.
+ Ta so sánh phần thập phân của hai số. Hàng phần mười của số 24,45; 24,15 lần lượt là 4 và 1.
Vì 1 < 4 nên 24,15 < 24,45, hay −24,15 > −24,45.
Do đó 35,18 > 21,75 > 0,6 > −24,15 > −24,45.
Vậy các số được sắp xếp thứ tự giảm dần là: 35,18; 21,75; 0,6; −24,15; −24,45.
Bài 5. Thực hiện các phép tính sau:
a) (−2,8) + 1,25;
b) 12,55 − 2,45 − (−4,6);
c) 14,5 . (−22,25);
d) (−18,24) : 2,4.
Lời giải:
a) (−2,8) + 1,25
= −(2,8 − 1,25)
= −1,55;
b) 12,55 − 2,45 − (−4,6)
= 10,1 − (−4,6)
= 10,1 + 4,6
= 14,7.
c) 14,5 . (−22,25)
= −(14,5 . 22,25)
= −322,625.
d) (−18,24) : 2,4
= −(18,24 : 2,4)
= −7,6.
Bài 6. Tính hợp lí:
a) 22,5 + (−11,75) + 7,5 + (−8,25);
b) 1,24 . (−4,5) + 1,24 . (−5,5).
Lời giải:
a) 22,5 + (−11,75) + 7,5 + (−8,25)
= 22,5 + 7,5 + (−11,75) + (−8,25) (Tính chất giao hoán)
= [22,5 + 7,5] + [(−11,75) + (−8,25)] (Tính chất kết hợp)
= 30 + (−20)
= 30 −20 = 10.
b) 1,24 . (−4,5) + 1,24 . (−5,5)
= 1,24 . [(−4,5) + (−5,5)]
= 1,24 . (−10)
= −(1,24 . 10)
= −12,4.
Bài 7. Tính chu vi hình tròn có bán kính R = 8,5 cm theo công thức C = 2πR với π = 3,142.
Lời giải:
Chu vi của hình tròn đó là:
C = 2πR = 2 . 3,142 . 8,5 = 53,414 (cm).
Vậy hình tròn có bán kính R = 8,5 cm có chu vi là 53,414 cm.
Bài 8. Làm tròn các số sau đây: −457,1631; 641,891
a) đến đơn vị;
b) đến hàng chục.
Lời giải:
a)
* Làm tròn số −457,1631 đến hàng đơn vị:
- Chữ số hàng đơn vị của số −457,1631 là 7.
- Chữ số bên phải liền nó là 1 < 5 nên chữ số hàng đơn vị giữ nguyên là 7, đồng thời bỏ các chữ số ở phần thập phân.
Do đó, số −457,1631 làm tròn đến hàng đơn vị là: −457.
* Làm tròn số 641,891 đến hàng đơn vị:
- Chữ số hàng đơn vị của số 641,891 là 1.
- Chữ số bên phải liền nó là 8 > 5 nên chữ số hàng đơn vị tang thêm một đơn vị là 2, đồng thời bỏ các chữ số ở phần thập phân.
Do đó, số 641,89 làm tròn đến hàng đơn vị là: 642.
Vậy các số −457,1631; 641,891 làm tròn đến hàng đơn vị lần lượt là −457 và 642.
b)
* Làm tròn số −457,1631 đến hàng chục:
- Chữ số hàng chục của số −457,1631 là 5.
- Chữ số bên phải liền nó là 7 > 5 nên chữ số hàng chục tăng lên một đơn vị là 6 đồng thời thay chữ số hàng đơn vị bằng số 0 và bỏ tất cả các chữ số ở phần thập phân.
Do đó, số −457,1631 làm tròn đến hàng chục là: −460.
* Làm tròn số 641,891 đến hàng chục:
- Chữ số hàng chục của số 641,891 là 4.
- Chữ số bên phải liền nó là 1 < 5 nên chữ số hàng chục giữ nguyên là 4, đồng thời thay chữ số hàng đơn vị bằng số 0 và bỏ tất cả các chữ số ở phần thập phân.
Do đó, số 641,89 làm tròn đến hàng chục là: 641.
Bài 9. Hết học kỳ I, điểm môn Toán của bạn Nam như sau:
Hệ số 1: 8; 9; 10; 7.
Hệ số 2: 9.
Hệ số 3: 8.
Em hãy tính điểm trung bình môn Toán học kì I của bạn Nam (làm tròn đến chữ số thập phân thứ nhất).
Lời giải:
Điểm trung bình = (Điểm hệ số 1 + 2 . điểm hệ số 2 + 3 . điểm hệ số 3) : 9.
Điểm trung bình môn Toán học kì I của bạn Nam là:
(8 + 9 + 10 + 7 + 9 . 2 + 8 . 3) : 9 = 8,44444………
* Làm tròn số 8,44444……… đến chữ số thập phân thứ nhất:
- Chữ số thập phân thứ nhất của số 8,44444……… là 4.
- Chữ số bên phải liền nó là 4 < 5 nên chữ số thập phân thứ nhất là 2 và bỏ đi tất cả chữ số từ chữ số thập phân thứ hai trở đi.
Do đó số 8,44444……… làm tròn đến chữ số thập phân thứ nhất là 8,4.
Vậy điểm trung bình môn Toán học kì I của bạn Nam (làm tròn đến chữ số thập phần thứ nhất) là 8,4.
Bài 10. Hãy ước lượng kết quả của phép tính sau rồi so sánh với kết quả tìm được bằng máy tính cầm tay.
(−44,16) : 12,8.
Lời giải:
* Ước lượng kết quả:
Ta có: −44,16 ≈ −44; 12,8 ≈ 13.
Do đó (−44,16) : 12,8 ≈ (−44) : 13 = 3,3846… ≈ 3
(chữ số thập phân thứ nhất là 3 < 5).
* Tính bằng máy tính cầm tay: (−44,16) : 12,8 = −3,45.
Nhận xét: Hai cách làm cho ta hai kết quả xấp xỉ nhau nhưng tính bằng máy tính cầm tay cho ta kết quả với độ chính xác cao hơn, còn ước lượng kết quả lại có thể tính nhẩm dễ dàng hơn.
Bài 11. Lớp 6A có 36 học sinh, trong đó có 20 học sinh nữ. Tính tỉ số giữa học sinh nam so với số học sinh cả lớp.
Lời giải:
Số học sinh nam của lớp 6A là:
36 −20 = 16 (học sinh).
Tỉ số giữa học sinh nam so với số học sinh cả lớp là:
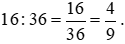
Vậy tỉ số giữa học sinh nam so với số học sinh cả lớp là 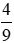 .
.
Bài 12. Viết các số thập phân sau đây dưới dạng tỉ số phần trăm:
−0,56; 7,5; −3,25.
Lời giải:
Các số thập phân được viết dưới dạng tỉ số phần trăm như sau:
−0,56 = −0,56 . 100% = −56%;
7,5 = 7,5 . 100% = 75%;
−3,25 = −12,25 . 100% = −325%.
Bài 13. Viết các phân số sau dưới dạng tỉ số phần trăm:
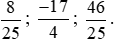
Lời giải:
Để viết các phân số dưới dạng tỉ số phần trăm, ta làm như sau:
Bước 1: Viết các phân số dưới dạng phân số có mẫu là 100.
Bước 2: Thêm kí hiệu % vào sau tử số của phân số mới.
Các phân số được viết dưới dạng tỉ số phần trăm là:

Bài 14. 50% mảnh vài dài 12,75m. Hỏi mảnh vải đó dài bao nhiêu mét?
Lời giải:
Mảnh vải đó dài là:
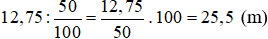
Vậy mảnh vải đó dài 25,5 m.
Bài 15. Trên đĩa có 48 quả táo. An ăn hết 25% số táo. Sau đó Bình ăn 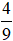 số táo còn lại. Hỏi trên đĩa còn bao nhiêu quả táo?
số táo còn lại. Hỏi trên đĩa còn bao nhiêu quả táo?
Lời giải:
Số quả táo An ăn hết là:
48 . 25% = 12 (quả táo)
Số quả táo còn lại sau khi An ăn hết 25% số táo là:
48 – 12 = 36 (quả táo)
Số quả táo Bình ăn hết là:
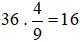 (quả táo)
(quả táo)
Số quả táo còn lại trên đĩa là:
36 – 16 = 20 (quả táo)
Vậy trên đĩa còn lại 20 quả táo.
Bài 16. Bác Nga gửi 600 triệu đồng vào ngân hàng theo hình thức không kì hạn với lãi suất 0,65% một năm. Sau 120 ngày, khi rút ra bác Nga nhận được bao nhiêu tiền cả vốn lẫn lãi?
Lời giải:
Cách tính tiền lãi không có kì hạn là:
Tính số tiền lãi = Số tiền gửi . lãi suất (% / năm) . số ngày thực gửi : 360.
Số tiền lãi bác Nga nhận được sau 120 ngày là:
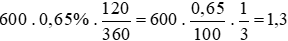 (triệu đồng).
(triệu đồng).
Sau 120 ngày, khi rút ra bác Nga nhận được số tiền cả vốn lẫn lãi là:
800 + 1,3 = 801,3 (triệu đồng) = 801 300 000 (đồng).
Vậy sau 120 ngày, khi rút ra bác Nga nhận được số tiền 801 300 000 đồng cả vốn lẫn lãi.
Học tốt Toán lớp 6 Chương 6
Các bài học để học tốt Chương 6 Toán lớp 6 hay khác:
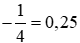 .
.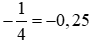 .
.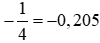 .
.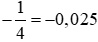 .
.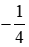 về dạng số thập phân rồi chọn phát biểu đúng, ta thực hiện:
về dạng số thập phân rồi chọn phát biểu đúng, ta thực hiện: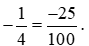
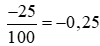 .
.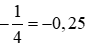
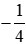 là phép chia (−1) cho 4. Thực hiện phép chia (−1) cho 4, ta được:
là phép chia (−1) cho 4. Thực hiện phép chia (−1) cho 4, ta được: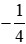 = (−1) : 4 = −(1 : 4) = −0,25.
= (−1) : 4 = −(1 : 4) = −0,25.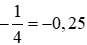 .
.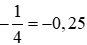 .
.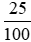 = 20.
= 20.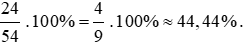
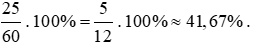
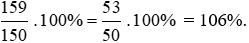
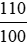 = 2 915 000 .
= 2 915 000 .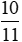 = 2 623 500 (đồng).
= 2 623 500 (đồng).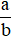 ).
).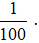
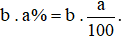 .
.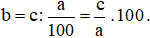 .
.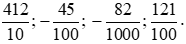
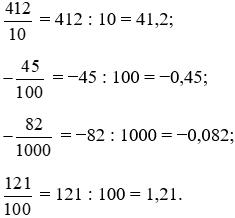
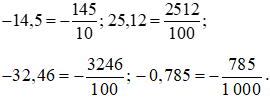
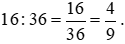
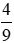
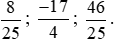

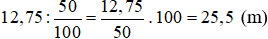
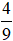 số táo còn lại. Hỏi trên đĩa còn bao nhiêu quả táo?
số táo còn lại. Hỏi trên đĩa còn bao nhiêu quả táo? 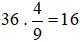 (quả táo)
(quả táo)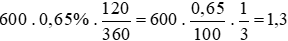 (triệu đồng).
(triệu đồng).