Bài 5 trang 68 Toán 6 Tập 2 Chân trời sáng tạo | Giải Toán lớp 6
Giải Toán lớp 6 Chân trời sáng tạo Bài tập cuối chương 7
Bài 5 trang 68 Toán lớp 6 Tập 2: Hai bạn Na và Toàn đứng đối diện nhau trên nền đất, ở giữa họ có một dãy các số và dấu cộng như hình dưới đây. Do vị trí khác nhau nên hai bạn thấy hai dãy phép tính khác nhau.

Hãy tìm cách điền hai chữ số vào hai ô trống để kết quả tính của hai bạn Na và Toàn bằng nhau.
Em nhận xét gì về hình ảnh mà hai bạn quan sát được.
Lời giải:
Ở vị trí của mỗi bạn sẽ nhìn thấy các phép tính khác nhau.
- Ở vị trí của Toàn nhìn thấy phép tính:
89 + 16 + 69 + 6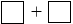 8 + 11.
8 + 11.
= 6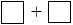 8 + 89 + 16 + 69 + 11 (Tính chất giao hoán).
8 + 89 + 16 + 69 + 11 (Tính chất giao hoán).
= (6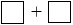 8) + (89 + 16 + 69 + 11) (Tính chất kết hợp).
8) + (89 + 16 + 69 + 11) (Tính chất kết hợp).
= 6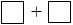 8 + 185.
8 + 185.
- Ở vị trí của Na nhìn thấy phép tính:
11 + 8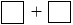 9 + 69 + 91 + 68.
9 + 69 + 91 + 68.
= 8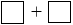 9 + 11 + 69 + 91 + 68 (Tính chất giao hoán).
9 + 11 + 69 + 91 + 68 (Tính chất giao hoán).
= (8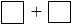 9) + (11 + 69 + 91 + 68) (Tính chất kết hợp).
9) + (11 + 69 + 91 + 68) (Tính chất kết hợp).
= 8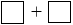 9 + 239.
9 + 239.
Để kết quả tính của hai bạn Na và Toàn bằng nhau thì:
6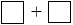 8 + 185 = 8
8 + 185 = 8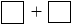 9 + 239.
9 + 239.
6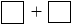 8 − 8
8 − 8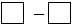 9 = 54.
9 = 54.
Gọi các ô trống thứ nhất, thứ hai, thứ ba và thứ tư lần lượt là a, b, c, d.
Như trên hình, ta thấy khi quay ngược số a sẽ được số d và quay ngược số b ra số c.
Ta có biểu thức sau:
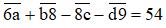
60 + a + 10b + 8 − (80 + c) − (10d + 9) = 54
60 + a + 10b + 8 − 80 − c − 10d − 9 = 54
a + 10b − c − 10d − 21 = 54
(a + 10b) − (c + 10d) = 75
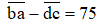
Trong hình vẽ trên, khi quay về phía mỗi bạn thì đều nhận được một phép tính có nghĩa.
Do đó, các chữ số a, b, c, d khi quay ngược lại vẫn tạo ra một số có nghĩa nên a, b, c, d và số 0 không được đứng đầu.
Do đó a, b, c, d
Trường hợp 1: a > c
Khi đó, a − c = 5 và b − d = 7.
- Số a, c thỏa mãn a − c = 5 và a, c nên a = 6; c = 1.
- Số b, d thỏa mãn b − d = 7 và a, c nên b = 8; d = 1.
Nhận thấy: quay ngược số a không ra được số d và quay ngược số b không ra được số c.
Do đó trường hợp này vô lý.
Trường hợp 1: a < c
Khi đó, 10 + a − c = 5 và b − d = 8 hay c − a = 5 và b − d = 8.
(a không trừ được cho c, mượn 10 đơn vị (hay 1 chục) ta có: 10 + a − c = 5, trả 1 vào hàng chục ta có: c − a = 5).
- Số a, c thỏa mãn c − a = 5 và a, c nên c = 6; a = 1.
- Số b, d thỏa mãn b − d = 8 và b, d nên b = 9; d = 1.
Nhận thấy: quay ngược số a ra được số d và quay ngược số b ra được số c.
Do đó trường hợp này thỏa mãn.
Từ đó suy ra, a = 1; b = 9; c = 6; d = 9.
Vậy phép tính cần điền là:
89 + 16 + 69 + 6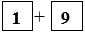 8 + 11 = 11 + 8
8 + 11 = 11 + 8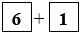 9 + 69 + 91 + 68
9 + 69 + 91 + 68
Hình ảnh mà hai bạn quan sát được là với mỗi số hạng, Na nhìn thấy chữ số ở hàng đơn vị thì Toàn nhìn thấy chữ số quay ngược lại ở hàng chục và ngược lại.
Lời giải bài tập Toán 6 Bài tập cuối chương 7 hay, chi tiết khác:
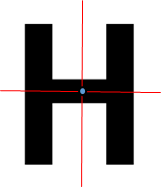






 8 + 11.
8 + 11. 8 + 89 + 16 + 69 + 11 (Tính chất giao hoán).
8 + 89 + 16 + 69 + 11 (Tính chất giao hoán).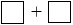 8) + (89 + 16 + 69 + 11) (Tính chất kết hợp).
8) + (89 + 16 + 69 + 11) (Tính chất kết hợp).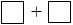 8 + 185.
8 + 185.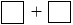 9 + 69 + 91 + 68.
9 + 69 + 91 + 68.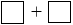 9 + 11 + 69 + 91 + 68 (Tính chất giao hoán).
9 + 11 + 69 + 91 + 68 (Tính chất giao hoán).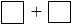 9) + (11 + 69 + 91 + 68) (Tính chất kết hợp).
9) + (11 + 69 + 91 + 68) (Tính chất kết hợp).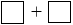 9 + 239.
9 + 239.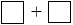 8 + 185 = 8
8 + 185 = 8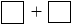 9 + 239.
9 + 239.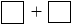 8
8 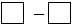 9 = 54.
9 = 54.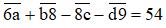
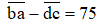
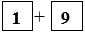 8 + 11 = 11 + 8
8 + 11 = 11 + 8 9 + 69 + 91 + 68
9 + 69 + 91 + 68