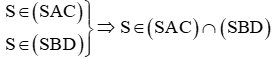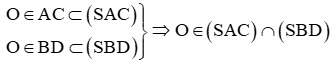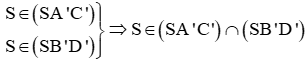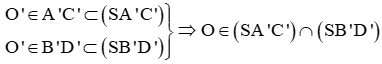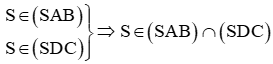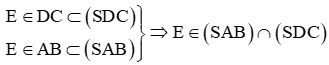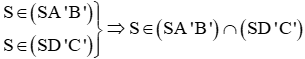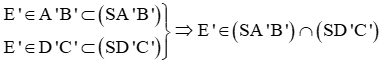Giải Toán 11 Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian - Chân trời sáng tạo
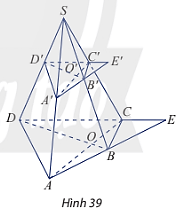
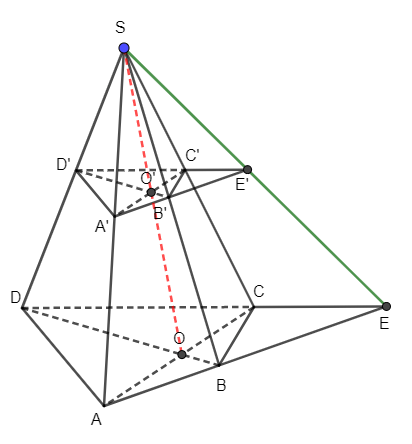
Vận dụng 4 trang 98 Toán 11 Tập 1: Cho hình chóp S.ABCD. Trên các cạnh bên của hình chóp lấy lần lượt các điểm A’, B’, C’, D’. Cho biết AC cắt BD tại O, A’C’ cắt B’D’ tại O’, AB cắt CD tại E và A’B’ cắt D’C’ tại E’ (Hình 39). Chứng minh rằng:
a) S, O’, O thẳng hàng;
b) S, E’, E thẳng hàng.
Lời giải:
a) +) Ta có
Ta lại có: O là giao điểm của AC và BD nên
Suy ra (SAC) ∩ (SBD) = SO.
+) Ta có
Ta lại có: O’ là giao điểm của A’C’ và B’D’ nên
Suy ra (SA'C') ∩ (SB'D') = SO'.
+) Mặt khác mặt phẳng (SA’C’) cũng chính là mặt phẳng (SAC), mặt phẳng (SB’D’) cũng chính là mặt phẳng (SBD) do đó SO’ trùng SO. Vì vậy S, O’, O thẳng hàng.
b) +) Ta có
Ta lại có: E là giao điểm của AB và DC nên
Suy ra (SAB) ∩ (SDC) = SE.
+) Ta có
Ta lại có: E’ là giao điểm của D’C’ và A’B’ nên
Suy ra (SB'C') ∩ (SD'C') = SE'.
+) Mặt khác mặt phẳng (SB’C’) cũng chính là mặt phẳng (SBC), mặt phẳng (SD’C’) cũng chính là mặt phẳng (SDC) do đó SE’ trùng SE. Vì vậy S, E’, E thẳng hàng.
Lời giải bài tập Toán 11 Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian hay, chi tiết khác: