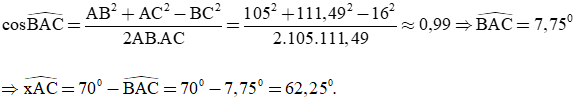Bài 3.8 trang 42 Toán 10 Tập 1 - Kết nối tri thức

Giải Toán 10 Kết nối tri thức Bài 6: Hệ thức lượng trong tam giác

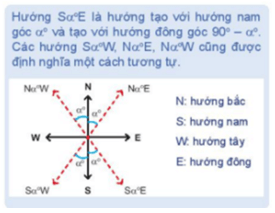
Bài 3.8 trang 42 Toán 10 Tập 1: Một tàu đánh cá xuất phát từ cảng A, đi theo hướng S70°E với vận tốc 70 km/h. Đi được 90 phút thì động cơ của tàu bị hỏng nên tàu trôi tự do theo hướng nam với vận tốc 8km/h. Sau 2 giờ kể từ khi động cơ bị hỏng, tàu neo đậu được vào một hòn đảo.

a) Tính khoảng cách từ cảng A tới đảo nơi tàu neo đậu.

b) Xác định hướng từ cảng A tới đảo nơi tàu neo đậu.

Lời giải:

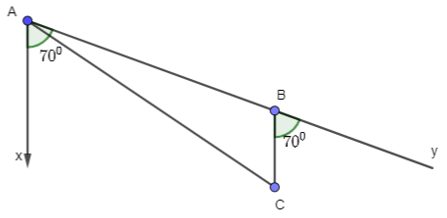
Ta có sơ đồ di chuyển của tàu như sau:

a) Tàu cá xuất phát từ A đi theo hướng S70⁰E với vận tốc 70km/h trong 90 phút = 1,5 giờ thì tàu cá đi được đến B (vị trí tàu bị hỏng), quãng đường AB là: 70.1,5 = 105 (km).

Từ vị trí B tàu cá trôi tự do với vận tốc 8km/h theo hướng nam sau 2h thì neo đậu vào đảo C, khi đó quãng đường BC là: 8.2 = 16km.

Khoảng cách từ cảng A đến nơi tàu neo đậu chính là đoạn AC.

Do tàu đi theo hướng S70⁰E nên phương AB hợp với phương nam Ax một góc 70⁰ nên $\widehat{xAB}={70}^0$.

Mà phương BC song song với phương nam Ax nên $\widehat{CBy}=\widehat{xAB}={70}^0$(hai góc đồng vị)

$\Rightarrow \widehat{ABC}={110}^0$ (Kề bù $\widehat{CBy}$)

Xét ΔABC, có:

AC² = AB² + AC² – 2AB.AC.cosB (định lí côsin)

= 105² + 16² – 2.105.16.cos110⁰

≈ 12 430,19

⇒ AC ≈ 111,49 km.

Vậy khoảng cách từ cảng A đến đảo nơi tàu neo đậu khoảng 111,49 km.

b) Xét ΔABC, có:

Vậy hướng từ cảng A đến đảo nơi tàu neo đậu là S62,25⁰E.

Lời giải bài tập Toán 10 Bài 6: Hệ thức lượng trong tam giác hay, chi tiết khác: