Bài 5 trang 92 Toán 10 Tập 1 Cánh diều

Giải Toán 10 Cánh diều Bài 5: Tích của một số với một vectơ

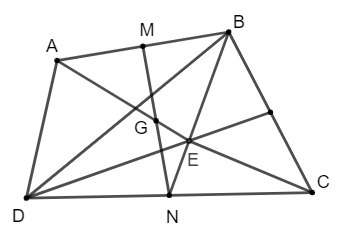
Bài 5 trang 92 Toán lớp 10 Tập 1: Cho tứ giác ABCD có M, N lần lượt là trung điểm của hai cạnh AB và CD. Gọi G là trung điểm của đoạn thẳng MN, E là trọng tâm của tam giác BCD. Chứng minh:

a) $\overrightarrow{EA}+\overrightarrow{EB}+\overrightarrow{EC}+\overrightarrow{ED}=4\overrightarrow{EG}$;

b) $\overrightarrow{EA}=4\overrightarrow{EG}$;

c) Điểm G thuộc đoạn thẳng AE và $\overrightarrow{AG}=\frac{3}{4}\overrightarrow{AE}$.

Lời giải:

a) Ta có M là trung điểm của AB nên $\overrightarrow{GA}+\overrightarrow{GB}=2\overrightarrow{GM}$.

Tương tự N là trung điểm CD nên $\overrightarrow{GC}+\overrightarrow{GD}=2\overrightarrow{GN\text{}}$.

Lại có G là trung điểm của MN nên $\overrightarrow{GM}+\overrightarrow{GN}=\overrightarrow{0}$.

Khi đó: $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=2\overrightarrow{GM}+2\overrightarrow{GN}=2\left(\overrightarrow{GM}+\overrightarrow{GN}\right)=\overrightarrow{0}$

Ta có:

$\overrightarrow{EA}+\overrightarrow{EB}+\overrightarrow{EC}+\overrightarrow{ED}$

$=\left(\overrightarrow{EG}+\overrightarrow{GA}\right)+\left(\overrightarrow{EG}+\overrightarrow{GB}\right)+\left(\overrightarrow{EG}+\overrightarrow{GC}\right)+\left(\overrightarrow{EG}+\overrightarrow{GD}\right)$

$=4\overrightarrow{EG}+\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}\right)$

=  $4\overrightarrow{EG}+\overrightarrow{0}$

$=4\overrightarrow{EG}$.

Vậy $\overrightarrow{EA}+\overrightarrow{EB}+\overrightarrow{EC}+\overrightarrow{ED}=4\overrightarrow{EG}$.

b) Do E là trọng tâm của tam giác BCD nên $\overrightarrow{EB}+\overrightarrow{EC}+\overrightarrow{ED}=\overrightarrow{0}$.

Thay vào câu a) ta có: $\overrightarrow{EA}+\overrightarrow{0}=4\overrightarrow{EG}$

Vậy $\overrightarrow{EA}=4\overrightarrow{EG}$.

c) Theo câu b ta có: $\overrightarrow{EA}=4\overrightarrow{EG}$ nên hai vectơ $\overrightarrow{EA},\overrightarrow{EG}$ cùng hướng và EA = 4EG hay EG < EA.

Do đó 3 điểm E, A, G thẳng hàng và G nằm giữa E và A.

Suy ra điểm G thuộc đoạn thẳng AE.

Vì EA = 4 EG nên AG = $\frac{3}{4}$AE.

Hai vectơ $\overrightarrow{AG}$ và $\overrightarrow{AE}$ cùng hướng.

Do đó: $\overrightarrow{AG}=\frac{3}{4}\overrightarrow{AE}$.

Lời giải bài tập Toán 10 Bài 5: Tích của một số với một vectơ hay, chi tiết khác: