Vận dụng 3 trang 70 Toán 10 Tập 2 Chân trời sáng tạo | Giải Toán 10

Giải Toán 10 Chân trời sáng tạo Bài 4: Ba đường conic trong mặt phẳng toạ độ

Vận dụng 3 trang 70 Toán lớp 10 Tập 2: Một cổng chào có hình parabol cao 10m và bề rộng của cổng tại chân cổng là 5m. Tính bề rộng của cổng tại chỗ cách đỉnh 2m.

Lời giải:

Ta vẽ parabol biểu diễn cho cổng chào như sau:

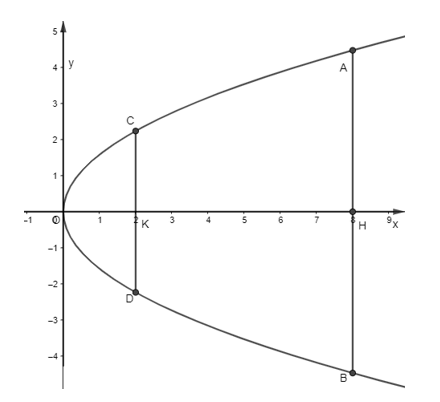
Gọi phương trình của parabol là y² = 2px.

Ta có chiều cao của cổng là OH = 10, bề rộng của cổng là AB = 5.

Khi đó A(10; 2,5), thay tọa độ điểm A vào parabol y² = 2px, ta được:

2,5² = 2p.10

⇔ $\frac{25}{4}$ = 20p

⇔ p = $\frac{25}{4.20}=\frac{5}{16}$

Suy ra parabol có phương tình y² = 2.$\frac{5}{16}$.x ⇔ y² = $\frac{5}{8}$.x

Tại vị trí điểm K cách đỉnh 2m bề rộng của cổng là đoạn CD.

Gọi C(2; y_C) (y_C > 0)

Vì C thuộc parabol nên tọa độ của C thỏa mãn y² = $\frac{5}{8}$.x nên ta có:

$y_C^2$ = $\frac{5}{8}$.2

⇔ $y_C^2$ = $\frac{5}{4}$

⇔ y_C = $\frac{\sqrt{5}}{2}$

⇒ C = (0; $\frac{\sqrt{5}}{2}$).

Khi đó CD = 2|y_C|= 2.$\frac{\sqrt{5}}{2}$ = $\sqrt{5}$ .

Vậy bề rộng của cộng tại chỗ cách đỉnh 2m là $\sqrt{5}$m.

Lời giải bài tập Toán 10 Bài 4: Ba đường conic trong mặt phẳng toạ độ hay, chi tiết khác: