Bài 6 trang 74 Toán 11 Tập 2 Chân trời sáng tạo

Giải Toán 11 Bài 3: Hai mặt phẳng vuông góc - Chân trời sáng tạo

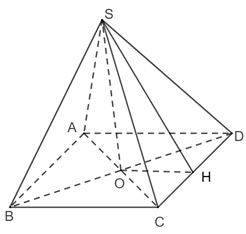
Bài 6 trang 74 Toán 11 Tập 2: Kim tự tháp bằng kính tại bảo tàng Louvre ở Paris có dạng hình chóp tứ giác đều với chiều cao là 21,6 m và cạnh đáy dài 34 m. Tính độ dài cạnh bên và diện tích xung quanh của kim tự tháp.

Lời giải:

Mô hình hoá hình ảnh kim tự tháp bằng hình chóp tứ giác đều S.ABCD có O là tâm của đáy.

Kẻ SH ⊥ CD (H $\in$ CD)

Ta có: SO = 21,6 m , AD = 34 m

$\mathrm{AC}=\sqrt{{\mathrm{AB}}^2+{\mathrm{BC}}^2}=34\sqrt{2}\left(m\right)\Rightarrow \mathrm{OC}=\frac{1}{2}\mathrm{AC}=17\sqrt{2}\left(m\right)$

ΔSOC vuông tại O $\Rightarrow \mathrm{SC}=\sqrt{{\mathrm{SO}}^2+{\mathrm{OC}}^2}\approx 32,3\left(m\right)$

Do đó độ dài cạnh bên bằng 32,3 m.

Tam giác SCD cân tại S

⇒ SH vừa là trung tuyến, vừa là đường cao của tam giác SCD

⇒ H là trung điểm của CD.

Mà O là trung điểm của AD.

⇒ OH là đường trung bình của tam giác ACD

⇒ $\mathrm{OH}=\frac{1}{2}\mathrm{AD}=17\left(m\right)$

Ta có: SO ⊥ (ABCD) $$SO ⊥ OH

⇒ ΔSOH vuông tại O.

⇒ $\mathrm{SH}=\sqrt{{\mathrm{SO}}^2+{\mathrm{OH}}^2}\approx 27,5\left(m\right)$

$S_{\mathrm{SCD}}=\frac{1}{2}.\mathrm{CD}.\mathrm{SH}\approx 467,5\left(m^2\right)$

Diện tích xung quanh của kim tự tháp là:
$S_{\mathrm{xq}}=4.S_{\mathrm{SCD}}=4.467,5\approx 1870\left(m^2\right)$.

Vậy độ dài cạnh bênlà 32,3 m và diện tích xung quanh của kim tự tháp là 1870 m².

Lời giải bài tập Toán 11 Bài 3: Hai mặt phẳng vuông góc hay, chi tiết khác: