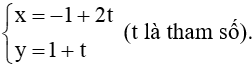Hoạt động 6 trang 85 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng

Hoạt động 6 trang 85 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ, cho đường thẳng ∆: 2x + y – 4 = 0 và điểm M(– 1; 1). Gọi H là hình chiếu của M lên đường thẳng ∆.

a) Tìm một vectơ chỉ phương của đường thẳng MH.

b) Viết phương trình tham số của đường thẳng MH.

c) Tìm tọa độ của H. Từ đó, tính độ dài đoạn thẳng MH.

Lời giải:

a) Đường thẳng ∆ có một vectơ pháp tuyến là $\overrightarrow{n_{\Delta }}=\left(2;1\right)$.

Do H là hình chiếu của M lên đường thẳng ∆ nên MH ⊥ ∆.

Khi đó giá của vectơ pháp tuyến $\overrightarrow{n_{\Delta }}=\left(2;1\right)$ song song hoặc trùng với đường thẳng MH.

Vậy một vectơ chỉ phương của đường thẳng MH là $\overrightarrow{u_{MH}}=\overrightarrow{n_{\Delta }}=\left(2;1\right)$.

b) Đường thẳng MH đi qua điểm M(– 1; 1) và có một vectơ chỉ phương là $\overrightarrow{u_{MH}}=\left(2;1\right)$ nên phương trình tham số của đường thẳng MH là

c) Điểm H thuộc đường thẳng MH nên gọi tọa độ H(– 1 + 2t; 1 + t).

Do H là hình chiếu của M lên ∆, do đó H cũng thuộc đường thẳng ∆ nên tọa độ điểm H thỏa mãn phương trình ∆, thay vào ta được:

2(– 1 + 2t) + (1 + t) – 4 = 0 ⇔ 5t – 5 = 0 ⇔ t = 1.

Do đó H(1; 2).

Vậy độ dài đoạn thẳng MH là MH = $\sqrt{{\left(1-\left(-1\right)\right)}^2+{\left(2-1\right)}^2}=\sqrt{5}$.

Lời giải Toán 10 Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng hay, chi tiết khác: