Hoạt động khám phá 8 trang 72 Toán 11 Tập 2 Chân trời sáng tạo

Giải Toán 11 Bài 3: Hai mặt phẳng vuông góc - Chân trời sáng tạo

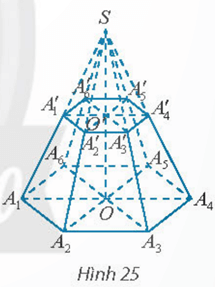
Hoạt động khám phá 8 trang 72 Toán 11 Tập 2: Cho hình chóp đều S.A₁A₂...A₆. Mặt phẳng (P) song song với mặt đáy và cắt các cạnh bên lần lượt tại A′₁A′₂...A′₆.

a) Đa giác A′₁A′₂...A′₆ có phái lục giác đều không? Giải thích.

b) Gọi O và O′ lần lượt là tâm của hai lục giác A₁A₂...A₆ và A′₁A′₂...A′₆. Đường thẳng OO′ có vuông góc với mặt đáy không?

Lời giải:

a) Ta có:(P) // (A₁A₂A₃...A₆)

Do đó A₁′A₂′ // A₁A₂; A₂′A₃′ // A₂A₃; A₃′A₄′ // A₃A₄;

A4′A5′ // A₄A₅; A₅′A₆′ // A₅A₆; A₆′A₁′ // A₆A₁

Khi đó $\frac{{A^{\text{'}}}_1{A^{\text{'}}}_2}{A_1{A}_2}=\frac{{A^{\text{'}}}_2{A^{\text{'}}}_3}{A_2{A}_3}=\frac{{A^{\text{'}}}_3{A^{\text{'}}}_4}{A_3{A}_4}=\frac{{A^{\text{'}}}_4{A^{\text{'}}}_5}{A_4{A}_5}=\frac{{A^{\text{'}}}_5{A^{\text{'}}}_6}{A_5{A}_6}=\frac{{A^{\text{'}}}_6{A^{\text{'}}}_1}{A_6{A}_1}$.

Mà A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ = A₅A₆ = A₆A₁

⇒ A₁′A₂′ = A₂′A₃′ = A₃′A₄′ = A₄′A₅′ = A₅′A₆′ = A₆′A₁′

Vậy đa giác A′₁A′₂...A′₆ là lục giác đều.

b) Ta có:

$\left.\begin{array}{c}\mathrm{O}\text{'}\in {{\mathrm{A}}^{\text{'}}}_1{{\mathrm{A}}^{\text{'}}}_4\subset \left(\text{S}{\mathrm{A}}_1{\mathrm{A}}_4\right)\\ \mathrm{O}\text{'}\in {{\mathrm{A}}^{\text{'}}}_3{{\mathrm{A}}^{\text{'}}}_6\subset \left({\mathrm{SA}}_3{\mathrm{A}}_6\right)\\ \left(\text{S}{\mathrm{A}}_1{\mathrm{A}}_4\right)\cap \left({\mathrm{SA}}_3{\mathrm{A}}_6\right)=\mathrm{SO}\end{array}\right\}\Rightarrow {\mathrm{O}}^{\text{'}}\in \mathrm{SO}$

Mà S.A₁A₂...A₆ là hình chóp đều nên SO ⊥ (A₁A₂...A₆ ).

Vậy OO′ ⊥ (A₁A₂...A₆).

Lời giải bài tập Toán 11 Bài 3: Hai mặt phẳng vuông góc hay, chi tiết khác: