Với giải bài tập Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn sách Cánh diều hay nhất, chi tiết giúp học sinh lớp 10 dễ dàng làm bài tập Toán 10 Bài 1.

Giải Toán 10 Cánh diều Bài 1: Bất phương trình bậc nhất hai ẩn

Video Giải Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn - Cô Diệu Minh (Giáo viên VietJack)

Giải Toán 10 trang 20 Tập 1

Câu hỏi khởi động

: Nhân dịp Tết Trung thu, một doanh nghiệp dự định sản xuất hai loại bánh

Giải Toán 10 Cánh diều Bài 1: Bất phương trình bậc nhất hai ẩn

Câu hỏi khởi động trang 20 Toán lớp 10 Tập 1: Nhân dịp Tết Trung thu, một doanh nghiệp dự định sản xuất hai loại bánh: bánh nướng và bánh dẻo. Lượng đường cần cho mỗi chiếc bánh nướng, bánh dẻo lần lượt là 60 g, 50 g. Doanh nghiệp đã nhập về 500 kg đường.

Số bánh nướng và số bánh dẻo doanh nghiệp dự định sản xuất cần thỏa mãn điều kiện ràng buộc gì để lượng đường sản xuất bánh không vượt quá lượng đường đã nhập về?

Lời giải:

Để tìm hiểu về câu hỏi này, chúng ta cùng theo dõi hoạt động 1 trang 20.

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Trong bài toán ở phần mở đầu, ta gọi x, y lần lượt là số bánh nướng

Giải Toán 10 Cánh diều Bài 1: Bất phương trình bậc nhất hai ẩn

Hoạt động 1 trang 20 Toán lớp 10 Tập 1: Trong bài toán ở phần mở đầu, ta gọi x, y lần lượt là số bánh nướng và số bánh dẻo doanh nghiệp dự định sản xuất (x, y là số tự nhiên). Nêu điều kiện ràng buộc đối với x và y để lượng đường sản xuất bánh không vượt quá lượng đường đã nhập về.

Lời giải:

Quan sát bài toán mở đầu, ta thấy số lượng đường nhập về và lượng đường cần để làm cho mỗi chiếc bánh chưa đưa về cùng đơn vị, do đó ta cần đổi đơn vị đo khối lượng. 

Đổi: 60 g = 0,06 kg; 50 g = 0,05 kg.

Làm một chiếc bánh nướng cần 0,06 kg đường, vậy làm x chiếc bánh nướng cần 0,06x (kg đường). 

Làm một chiếc bánh dẻo cần 0,05 kg đường, vậy làm y chiếc bánh dẻo cần 0,05y (kg đường). 

Tổng số đường để làm số bánh nướng và bánh dẻo mà công ti dự định sản xuất là: 

0,06x + 0,05y (kg đường)

Vì doanh nghiệp nhập về 500 kg đường, nên tổng số đường cần để làm các loại bánh theo dự định phải không quá 500 kg. 

Vậy điều kiện ràng buộc đối với x và y là: 0,06x + 0,05y ≤ 500. 

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Tìm bất phương trình bậc nhất hai ẩn trong các bất phương trình sau

Giải Toán 10 Cánh diều Bài 1: Bất phương trình bậc nhất hai ẩn

Luyện tập 1 trang 21 Toán lớp 10 Tập 1: Tìm bất phương trình bậc nhất hai ẩn trong các bất phương trình sau và chỉ ra một nghiệm của bất phương trình bậc nhất hai ẩn đó:

a) 5x + 3y < 20;

b) 3x –  $\frac{5}{y}$> 2.

Lời giải:

+ Bất phương trình bậc nhất hai ẩn x, y là bất phương trình có một trong các dạng sau:

ax + by < c; ax + by > c; ax + by ≤ c; ax +by ≥ c,

trong đó a, b, c là những số cho trước với a, b không đồng thời bằng 0, x và y là các ẩn.

Do đó trong hai bất phương trình đã cho, chỉ có bất phương trình a) 5x + 3y < 20 là bất phương trình bậc nhất hai ẩn.

 + Để chỉ ra nghiệm của bất phương trình bậc nhất hai ẩn trên, ta chỉ cần chọn cặp số (x₀; y₀) thỏa mãn 5x₀ + 3y₀ < 20.

Chẳng hạn, chọn x₀ = 1, y₀ = 1, ta có: 5 . 1 + 3 . 1 = 8 < 20

Vậy (1; 1) là một nghiệm của của bất phương trình bậc nhất hai ẩn 5x + 3y < 20.

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Trong mặt phẳng tọa độ Oxy, xác định các điểm M(x; y) mà

Giải Toán 10 Cánh diều Bài 1: Bất phương trình bậc nhất hai ẩn

Hoạt động 2 trang 21 Toán lớp 10 Tập 1: Trong mặt phẳng tọa độ Oxy, xác định các điểm M(x; y) mà:

a) x > 0 (1); 

b) y < 1 (2). 

Lời giải:

Để xác định điểm M(x; y) trong mặt phẳng tọa độ thỏa mãn điều kiện đã cho, ta làm như sau: 

a) Đường thẳng x = 0 chính là trục tung. 

Đường thẳng x = 0 chia mặt phẳng thành 2 nửa: nửa mặt phẳng bên trái và nửa mặt phẳng bên phải trục tung. 

Một điểm có hoành độ dương thì nằm ở nửa mặt phẳng bên phải trục tung và ngược lại. Vì thế, miền nghiệm của bất phương trình (1) là nửa mặt phẳng bên phải trục tung, được mô tả bằng nửa mặt phẳng không bị gạch ở Hình 1 (không kể trục tung).

b) Vẽ đường thẳng y = 1. 

Đường thẳng d: y = 1 chia mặt phẳng thành hai nửa: nửa mặt phẳng bên trên và nửa mặt phẳng bên dưới đường thẳng d (không kể đường thẳng d). 

Một điểm có tung độ nhỏ hơn 1 thì nằm ở nửa mặt phẳng bên dưới đường thẳng d và ngược lại. Vì thế, miền nghiệm của bất phương trình (2) là nửa mặt phẳng bên dưới đường thẳng d, được mô tả bằng nửa mặt phẳng không bị gạch ở Hình 2. 

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Cho bất phương trình 2x – y > 2 (3). Trong mặt phẳng tọa độ Oxy, vẽ đường thẳng d

Giải Toán 10 Cánh diều Bài 1: Bất phương trình bậc nhất hai ẩn

Hoạt động 3 trang 22 Toán lớp 10 Tập 1: Cho bất phương trình 2x – y > 2 (3).

a) Trong mặt phẳng tọa độ Oxy, vẽ đường thẳng d: 2x – y = 2 ⇔ y = 2x – 2. 

b) Xét điểm M(2; – 1). Chứng tỏ (2; – 1) là nghiệm của bất phương trình (3). 

c) Đường thẳng d chia mặt phẳng tọa độ thành hai nửa mặt phẳng. Gạch đi nửa mặt phẳng không chứa điểm M(2; – 1). 

Lời giải:

a) Đường thẳng d: y = 2x – 2

Cho x = 0 thì y = – 2

Cho y = 0 thì x = 1

Do đó, đường thẳng d đi qua hai điểm (0; – 2) và (1; 0). Ta vẽ đường thẳng d như sau: 

b) Xét điểm M(2; – 1).

Thay x = 2 và y = – 1 vào bất phương trình (3) ta được: 2 . 2 – (– 1) > 2 ⇔ 5 > 2 (luôn đúng). 

Vậy (2; – 1) là nghiệm của bất phương trình (3). 

c) Ta vẽ như hình dưới: 

Miềm nghiệm của bất phương trình (3) là nửa mặt phẳng không bị gạch trong hình trên. 

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Biểu diễn miền nghiệm của mỗi bất phương trình sau: x – 2y <4

Giải Toán 10 Cánh diều Bài 1: Bất phương trình bậc nhất hai ẩn

Luyện tập 2 trang 24 Toán lớp 10 Tập 1: Biểu diễn miền nghiệm của mỗi bất phương trình sau:

a) x – 2y < 4;

b) x + 3y ≥ 6. 

Lời giải:

a) x – 2y < 4 

+ Vẽ đường thẳng d: x – 2y = 4

Cho x = 0 thì y = – 2, cho y = 0 thì x = 4. Đường thẳng d đi qua 2 điểm (0; – 2) và (4; 0). 

+ Lấy điểm O(0; 0). Ta có: 0 – 0 = 0 < 4. 

Vậy miền nghiệm của bất phương trình x – 2y < 4 là nửa mặt phẳng không bị gạch ở hình trên chứa điểm O(0; 0) không kể đường thẳng d.

b) x + 3y ≥ 6

+ Vẽ đường thẳng d: x + 3y = 6

Cho x = 0 thì y = 2, cho y = 0 thì x = 6, do đó đường thẳng d đi qua hai điểm (0; 2) và (6; 0). 

+ Lấy điểm O(0; 0). Ta có: 0 + 3.0 = 0 < 6. 

Vậy miền nghiệm của bất phương trình x + 3y ≥ 6 là nửa mặt phẳng không bị gạch ở hình trên chứa điểm O(0; 0) kể cả đường thẳng d. 

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Cặp số nào sau đây là nghiệm của bất phương trình 2x – 3y < 3

Giải Toán 10 Cánh diều Bài 1: Bất phương trình bậc nhất hai ẩn

Bài 1 trang 24 Toán lớp 10 Tập 1: Cặp số nào sau đây là nghiệm của bất phương trình 2x – 3y < 3?

a) (0; – 1); 

b) (2; 1); 

c) (3; 1). 

Lời giải:

Ta có: 2x – 3y < 3 (1).

a) Thay x = 0, y = – 1 vào bất phương trình (1) ta được: 2 . 0 – 3 . (– 1) < 3 

⇔ 3 < 3 (vô lí) 

Vậy cặp số (0; – 1) không phải là nghiệm của bất phương trình đã cho. 

b) Tương tự ta có: 2 . 2 – 3 . 1 = 4 – 3 = 1 < 3 (luôn đúng)

Vậy cặp số (2; 1) là một nghiệm của bất phương trình đã cho. 

c) Ta có: 2 . 3 – 3 . 1 = 6 – 3 = 3 < 3 (vô lí). 

Vậy cặp số (3; 1) không phải là nghiệm của bất phương trình đã cho.

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Biểu diễn miền nghiệm của mỗi bất phương trình sau: x + 2y < 3

Giải Toán 10 Cánh diều Bài 1: Bất phương trình bậc nhất hai ẩn

Bài 2 trang 24 Toán lớp 10 Tập 1: Biểu diễn miền nghiệm của mỗi bất phương trình sau:

a) x + 2y < 3; 

b) 3x – 4y ≥ – 3; 

c) y ≥ – 2x + 4; 

d) y < 1 – 2x. 

Lời giải:

a) x + 2y < 3 

+ Vẽ đường thẳng d: x + 2y = 3.

+ Lấy điểm O(0; 0). Ta có: 0 + 2.0 = 0 < 3.

Vậy miền nghiệm của bất phương trình x + 2y < 3 là nửa mặt phẳng không bị gạch ở hình trên chứa điểm O(0; 0) không kể đường thẳng d. 

b) 3x – 4y ≥ – 3

+ Vẽ đường thẳng d: 3x – 4y = – 3. 

+ Lấy điểm O(0; 0). Ta có: 3 . 0 – 4 . 0 = 0 > – 3. 

Vậy miền nghiệm của bất phương trình 3x – 4y ≥ – 3 là nửa mặt phẳng không bị gạch ở hình trên chứa điểm O(0; 0) kể cả đường thẳng d. 

c) y ≥ – 2x + 4 

⇔ 2x + y ≥ 4 

+ Vẽ đường thẳng d: 2x + y = 4. 

+ Lấy điểm O(0; 0). Ta có: 2 . 0 + 0 = 0 < 4. 

Vậy miền nghiệm của bất phương trình 2x + y ≥ 4 hay chính là y ≥ – 2x + 4 là nửa mặt phẳng không bị gạch ở hình trên không chứa điểm O(0; 0) kể cả đường thẳng d. 

d) y < 1 – 2x 

⇔ 2x + y < 1

+ Vẽ đường thẳng d: 2x + y = 1. 

+ Lấy O(0; 0). Ta có: 2 . 0 + 0 = 0 < 1. 

Vậy miền nghiệm của bất phương trình 2x + y < 1 hay chính là y < 1 – 2x là nửa mặt phẳng không bị gạch ở hình trên chứa điểm O(0; 0) không kể đường thẳng d. 

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Phần không gạch (không kể d) ở mỗi Hình 7a, 7b, 7c là miền nghiệm của bất phương trình nào?

Giải Toán 10 Cánh diều Bài 1: Bất phương trình bậc nhất hai ẩn

Bài 3 trang 24 Toán lớp 10 Tập 1: Phần không gạch (không kể d) ở mỗi Hình 7a, 7b, 7c là miền nghiệm của bất phương trình nào?

Lời giải:

a) Giả sử đường thẳng d: y = ax + b (1) (a ≠ 0)

Quan sát Hình 7a, ta thấy đường thẳng d đi qua hai điểm (0; – 2) và (2; 0).

Thay x = 0, y = – 2 vào (1) ta được: – 2 = b hay b = – 2

Thay x = 2, y = 0 vào (1) ta được: 0 = 2a + b

Suy ra 2a = – b = 2 ⇒ a = 1 (t/m).

Khi đó đường thẳng d: y = x – 2 ⇔ x – y = 2

Xét điểm O(0; 0), ta có: 0 – 0 = 0 < 2

Lại có trên Hình 7a điểm O(0; 0) thuộc phần gạch sọc.

Vậy phần không gạch (không kể d) là miền nghiệm của bất phương trình x – y > 2.

b) Giả sử đường thẳng d: y = ax + b (2) (a ≠ 0)

Quan sát Hình 7b, ta thấy đường thẳng d đi qua 2 điểm (0; 1) và (2; 0).

Thay x = 0, y = 1 vào (2), ta được: b = 1

Thay x = 2, y = 0 vào (2), ta được: 2a + b = 0

Suy ra 2a + 1 = 0 ⇔ a =  $-\frac{1}{2}$(t/m)

Khi đó đường thẳng d: y =  $-\frac{1}{2}x$+ 1 ⇔ x + 2y = 2

Xét điểm O(0; 0). Ta có: 0 + 0 = 0 < 2.

Lại có trên Hình 7b điểm O(0; 0) thuộc phần gạch sọc.

Vậy phần không gạch sọc (không kể d) là miền nghiệm của bất phương trình x + 2y > 2.

c) Quan sát Hình 7c, ta thấy đường thẳng d đi qua gốc tọa độ và đi qua điểm M(1; 1).

Do đó phương trình đường thẳng d có dạng: y = ax (a ≠ 0)

Vì d đi qua M nên thay x = 1, y = 1 vào y = ax, ta được: a = 1 (t/m)

Do đó đường thẳng d: y = x ⇔ x – y = 0

Xét điểm (1; 0). Ta có: 1 – 0 = 1 > 0.

Lại có trên Hình 7c điểm (1; 0) nằm trên phần gạch sọc.

Vậy phần không gạch sọc (không kể d) là miền nghiệm của bất phương trình x – y < 0.

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Một gian hàng trưng bày bàn và ghế rộng 60 m^2. Diện tích để kê một chiếc ghế là 0,5 m^2

Giải Toán 10 Cánh diều Bài 1: Bất phương trình bậc nhất hai ẩn

Bài 4 trang 24 Toán lớp 10 Tập 1: Một gian hàng trưng bày bàn và ghế rộng 60 m². Diện tích để kê một chiếc ghế là 0,5 m², một chiếc bàn là 1,2 m². Gọi x là số chiếc ghế, y là số chiếc bàn được kê.

a) Viết bất phương trình bậc nhất hai ẩn x, y cho phần mặt sàn để kê bàn và ghế biết diện tích mặt sàn dành cho lưu thông tối thiểu là 12m².

b) Chỉ ra ba nghiệm của bất phương trình trên.

Lời giải:

a) Điều kiện: $x\in \mathbb{N},y\in \mathbb{N}$

Vì diện tích mặt sàn dành cho lưu thông tối thiểu là 12 m², do đó diện tích phần mặt sàn để kê bàn và ghế tối đa là: 60 – 12 = 48 (m²).

Diện tích để kê một chiếc ghế là 0,5 m², nên diện tích để kê x chiếc ghế là 0,5x (m²).

Diện tích để kê một chiếc bàn là 1,2 m², nên diện tích để kê y chiếc bàn là 1,2y (m²).

Tổng diện tích cho phần mặt sàn để kê x chiếc ghế và y chiếc bàn là: 0,5x + 1,2y (m²).

Do đó, bất phương trình cần tìm là: 0,5x + 1,2y ≤ 48.

b) Cặp số (x₀; y₀) là nghiệm của bất phương trình 0,5x + 1,2y ≤ 48 nếu 0,5x₀ + 1,2y₀ ≤ 48. (chú ý x₀ và y₀ ­là các số tự nhiên, do đây là số chiếc bàn và ghế)

+ Chọn x₀ = 2, y₀ =  5, ta có: 0,5 . 2 + 1,2 . 5 = 1 + 6 = 7 < 48.

+ Chọn x₀ = 4, y₀ = 10, ta có: 0,5 . 4 + 1,2 . 10 = 2 + 12 = 14 < 48.

+ Chọn x₀ = 6, y_0­ = 20, ta có: 0,5 . 6 + 1,2 . 20 = 3 + 24 = 27 < 48.

Vậy ba cặp số (2; 5), (4; 10), (6; 20) là ba nghiệm của bất phương trình 0,5x + 1,2y ≤ 48.

Chú ý: Bất phương trình bậc nhất hai ẩn có vô số nghiệm, nên có thể chọn cặp số tùy ý thỏa mãn.

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Trong 1 lạng (100 g) thịt bò chứa khoảng 26 g protein, 1 lạng cá rô phi chứa khoảng 20 g protein

Giải Toán 10 Cánh diều Bài 1: Bất phương trình bậc nhất hai ẩn

Bài 5 trang 24 Toán lớp 10 Tập 1: Trong 1 lạng (100 g) thịt bò chứa khoảng 26 g protein, 1 lạng cá rô phi chứa khoảng 20 g protein. Trung bình trong một ngày, một người phụ nữ cần tối thiểu 46 g protein. (Nguồn: https://vinmec.com và https://thanhnien.vn) Gọi x, y lần lượt là số lạng thịt bò và số lạng cá rô phi mà một người phụ nữ nên ăn trong một ngày. Viết bất phương trình bậc nhất hai ẩn x, y để biểu diễn lượng protein cần thiết cho một người phụ nữ trong một ngày và chỉ ra ba nghiệm của bất phương trình đó.

Lời giải:

Trong 1 lạng thịt bò chứa khoảng 26 g protein nên trong x lạng thịt bò chứa khoảng 26x (g protein). 

Trong 1 lạng cá rô phi chứa khoảng 20 g protein nên trong y lạng cá rô phi chứa khoảng 20y (g protein). 

Tổng số lượng protein mà một người phụ nữ nên ăn trong một ngày là: 26x + 20y (g protein). 

Trung bình mỗi ngày, một người phụ nữ cần tối thiểu 46 g protein. 

Do đó, bất phương trình bậc nhất hai ẩn x, y để biểu diễn lượng protein cần thiết cho một người phụ nữ trong một ngày là: 26x + 20y ≥ 46. 

Cặp số (x₀; y₀) là nghiệm của bất phương trình 26x + 20y ≥ 46 nếu 26x₀ + 20y₀ ≥ 46. 

+ Chọn x₀ = 1, y₀ = 1, ta có: 26 . 1 + 20 . 1 = 46  

+ Chọn x₀ = 2, y₀ = 1, ta có: 26 . 2 + 20 . 1 = 72 > 46 

+ Chọn x₀ = 1, y₀ = 2, ta có: 26 . 1 + 20 . 2 = 66 > 46

Vậy ba cặp số (1; 1), (2; 1), (1; 2) là ba nghiệm của bất phương trình 26x + 20y ≥ 46. 

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Sách bài tập Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn - Cánh diều

Với giải sách bài tập Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 Bài 1.

Sách bài tập Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn - Cánh diều

Giải SBT Toán 10 trang 24 Tập 1

Bất phương trình bậc nhất hai ẩn (Lý thuyết Toán lớp 10) - Cánh diều

Với tóm tắt lý thuyết Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.

Bất phương trình bậc nhất hai ẩn (Lý thuyết Toán lớp 10) - Cánh diều

Lý thuyết Bất phương trình bậc nhất hai ẩn

1. Bất phương trình bậc nhất hai ẩn

• Bất phương trình bậc nhất hai ẩn x, y là bất phương trình có một trong các dạng sau:

ax + by < c;           ax + by > c

ax + by ≤ c;            ax + by ≥ c

trong đó:    x, y là các ẩn,

a, b, c là các số cho trước (tham số) với a, b không đồng thời bằng 0.

Ví dụ:

+) $\frac{5}{3}x+\sqrt{2}y<5$ có dạng bất phương trình bậc nhất hai ẩn x và y với $a=\frac{5}{3}$, $b=\sqrt{2}$ và c = 5. Do đó bất phương trình này là bất phương trình bậc nhất hai ẩn.

+ $3x-\frac{5}{y}\ge 2$ không phải bất phương trình bậc nhất hai ẩn, vì không có dạng bất phương trình bậc nhất hai ẩn .

• Cho bất phương trình bậc nhất hai ẩn ax + by < c (*).

Mỗi cặp số (x₀ ; y₀) sao cho ax₀ + by₀ < c gọi là một nghiệm của bất phương trình (*).

Trong mặt phẳng toạ độ Oxy, tập hợp tất cả các điểm có toạ độ là nghiệm của bất phương trình (*) được gọi là miền nghiệm của bất phương trình đó.

Nghiệm và miền nghiệm của các bất phương trình dạng ax + by > c; ax + by ≤ c và             ax + by ≥ c được định nghĩa tương tự.

Ví dụ: Xét bất phương trình 2x + y ≤ 3:

+ (1 ; 1) là một nghiệm của bất phương trình vì 2 . 1 + 1 = 3 ≤ 3 là mệnh đề đúng.

+ (–2 ; 10) không là nghiệm của bất phương trình vì 2 . (–2) + 10 = 6 ≤ 3 là mệnh đề sai.

+ (2 ; –5) là nghiệm của bất phương trình vì 2 . 2 – 5 = –1 ≤ 3 là mệnh đề đúng.

2. Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn:

• Trong mặt phẳng toạ độ Oxy, đường thẳng d: ax + by = c chia mặt phẳng thành hai nửa mặt phẳng. Một trong hai nửa mặt phẳng (không kể d) là miền nghiệm của bất phương trình ax + by < c, nửa mặt phẳng còn lại (không kể d) là miền nghiệm của bất phương trình ax + by > c.

Chú ý: Đối với bất phương trình dạng ax + by ≤ c hoặc ax + by ≥ c thì miền nghiệm là nửa mặt phẳng kể cả đường thẳng d.

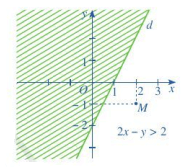
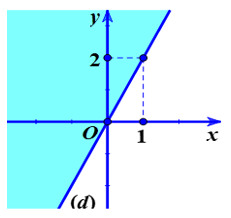
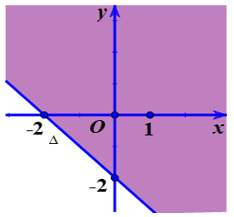
Ví dụ: Đường thẳng d: 2x – 3y = 6 chia mặt phẳng Oxy thành hai nửa mặt phẳng như hình dưới. Hỏi nửa mặt không bị gạch (không kể đường thẳng d) là miền nghiệm của bất phương trình nào?

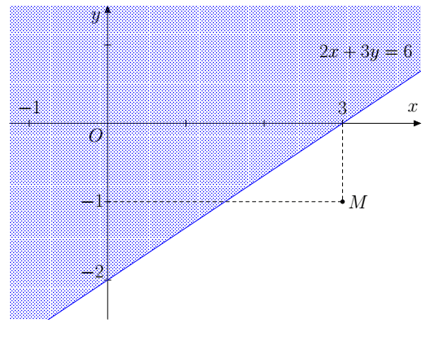
Hướng dẫn giải:

Lấy một giá trị nằm trong nửa mặt phẳng không bị gạch, ví dụ điểm M(3 ; –1). Thay toạ độ điểm M vào vế trái phương trình đường thẳng d, ta thấy:

2x_M – 3y_M = 2 . 3 – 3 . (–1) = 9 > 6

Như vậy, M là một nghiệm của bất phương trình 2x – 3y > 6, miền không bị gạch (không kể d) là miền nghiệm của bất phương trình 2x – 3y > 6.

Vậy miền không bị gạch (không kể đường thẳng d) là miền nghiệm của bất phương trình 2x – 3y > 6.

• Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn:

Bước 1. Vẽ đường thẳng d: ax + by = c. Đường thẳng d chia mặt phẳng toạ độ thành hai nửa mặt phẳng.

Bước 2. Lấy một điểm M(x₀; y₀) không nằm trên d (thường lấy gốc toạ độ O nếu c ≠ 0). Tính ax₀ + by₀ và so sánh với c.

Bước 3.   Kết luận:

+) Nếu ax₀ + by₀ < c thì nửa mặt phẳng chứa điểm M (không kể d) là miền nghiệm của bất phương trình ax + by < c.

+) Nếu ax₀ + by₀ > c thì nửa mặt phẳng chứa điểm M (không kể d) là miền nghiệm của bất phương trình ax + by > c.

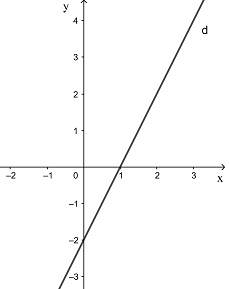
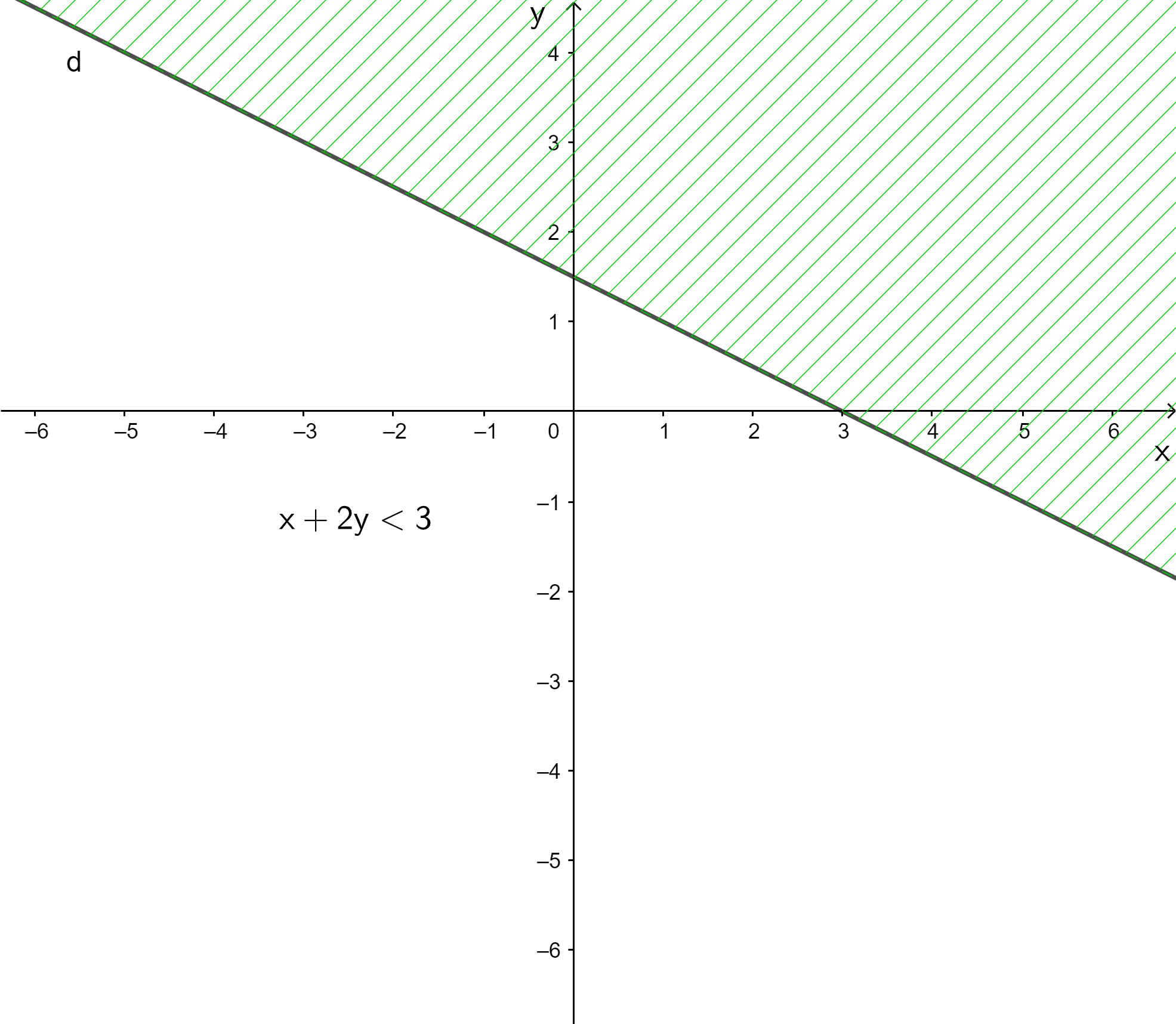
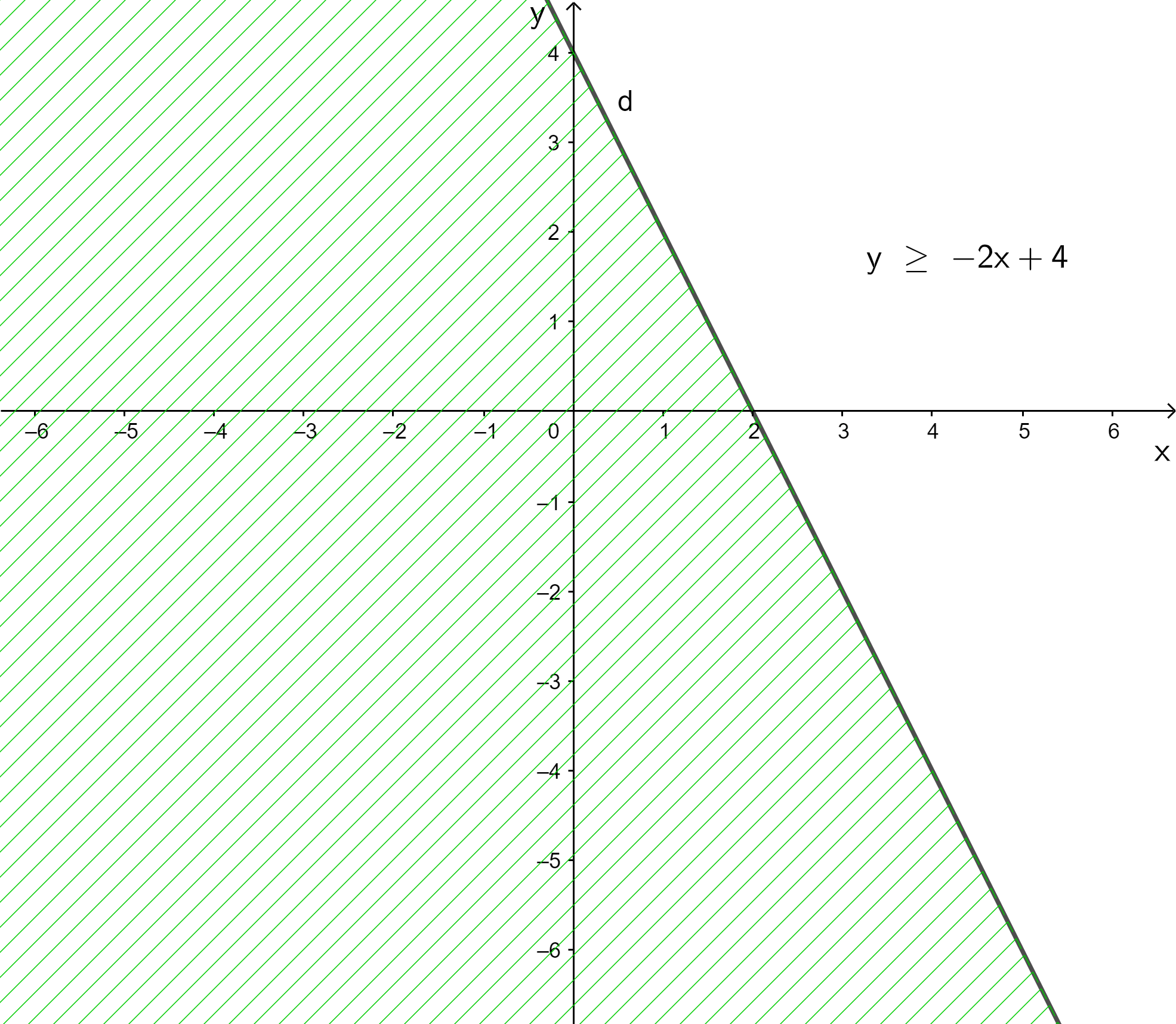
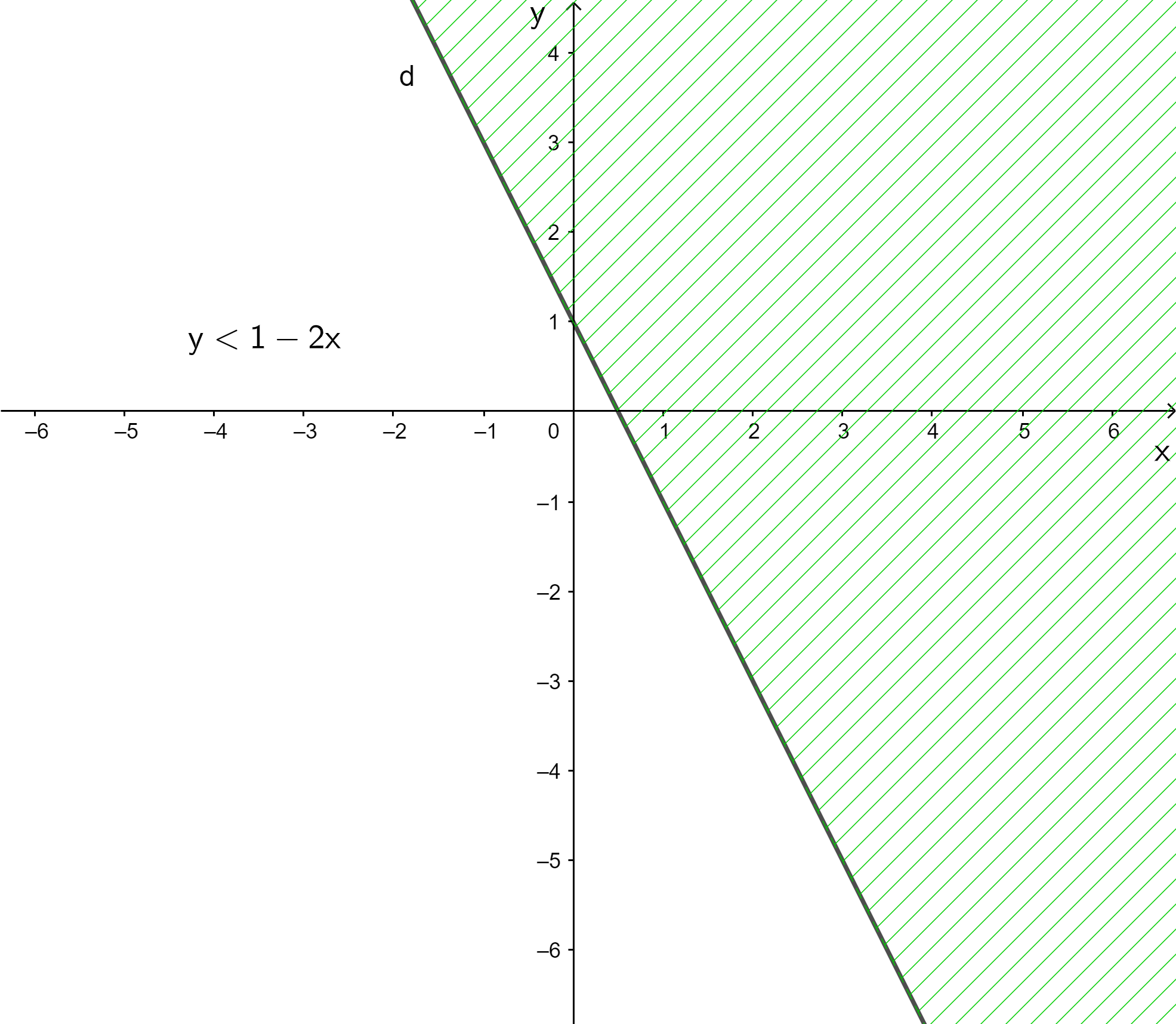
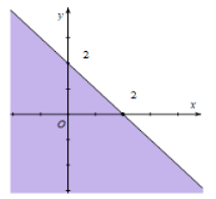
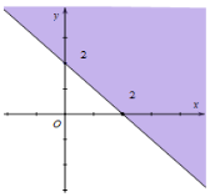
Ví dụ: Biểu diễn miền nghiệm của bất phương trình x + 3y < 3 và x + 3y ≤ 3.

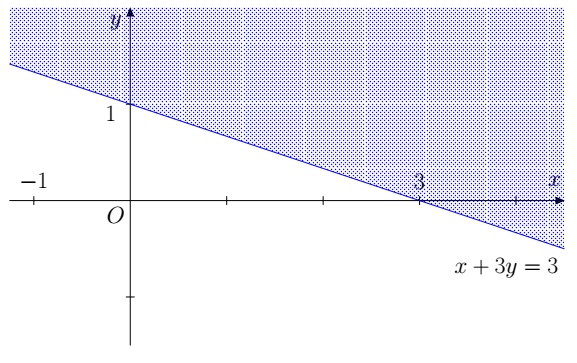
+ Vẽ đường thẳng d: x + 3y = 3

+ Lấy điểm O(0; 0). Ta có: 0 + 3 . 0 = 0 < 3.

+ Vậy:

Miền nghiệm của bất phương trình x + 3y < 3 là nửa mặt phẳng chứa điểm O không kể đường thẳng d.

Miền nghiệm của bất phương trình x + 3y ≤ 3 là nửa mặt phẳng chứa điểm O gồm cả đường thẳng d.

Bài tập Bất phương trình bậc nhất hai ẩn

Bài 1. Điểm nào trong các điểm A(3 ; –2), B(3 ; 5), C(2 ; 1) nằm trên miền nghiệm của bất phương trình 4x – 3y < 5?

Hướng dẫn giải:

Lần lượt thay toạ độ các điểm  A(3 ; –2), B(3 ; 5), C(2 ; 1) vào bất phương trình, ta có:

4 . 3 – 3 . (–2) = 18 < 5 là mệnh đề sai. Do đó điểm A không nằm trên miền nghiệm.

4 . 3 – 3 . 5 = –3 < 5 là mệnh đề đúng. Do đó điểm B nằm trên miền nghiệm.

4 . 2 – 3 . 1 = 5 < 5 là mệnh đề sai. Do đó điểm C không nằm trên miền nghiệm.

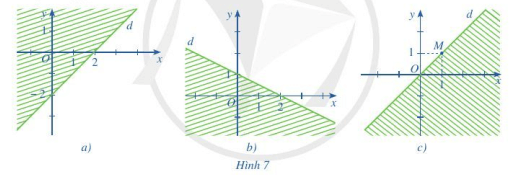
Bài 2. Biểu diễn miền nghiệm của mỗi bất phương trình sau:

a) $\frac{x}{3}+\frac{y}{2}<-1$                          

b) $x-\frac{3y}{2}\le 0$                          

c) $\frac{x+y}{2}\ge \frac{2x-y+1}{3}$ 

Hướng dẫn giải:

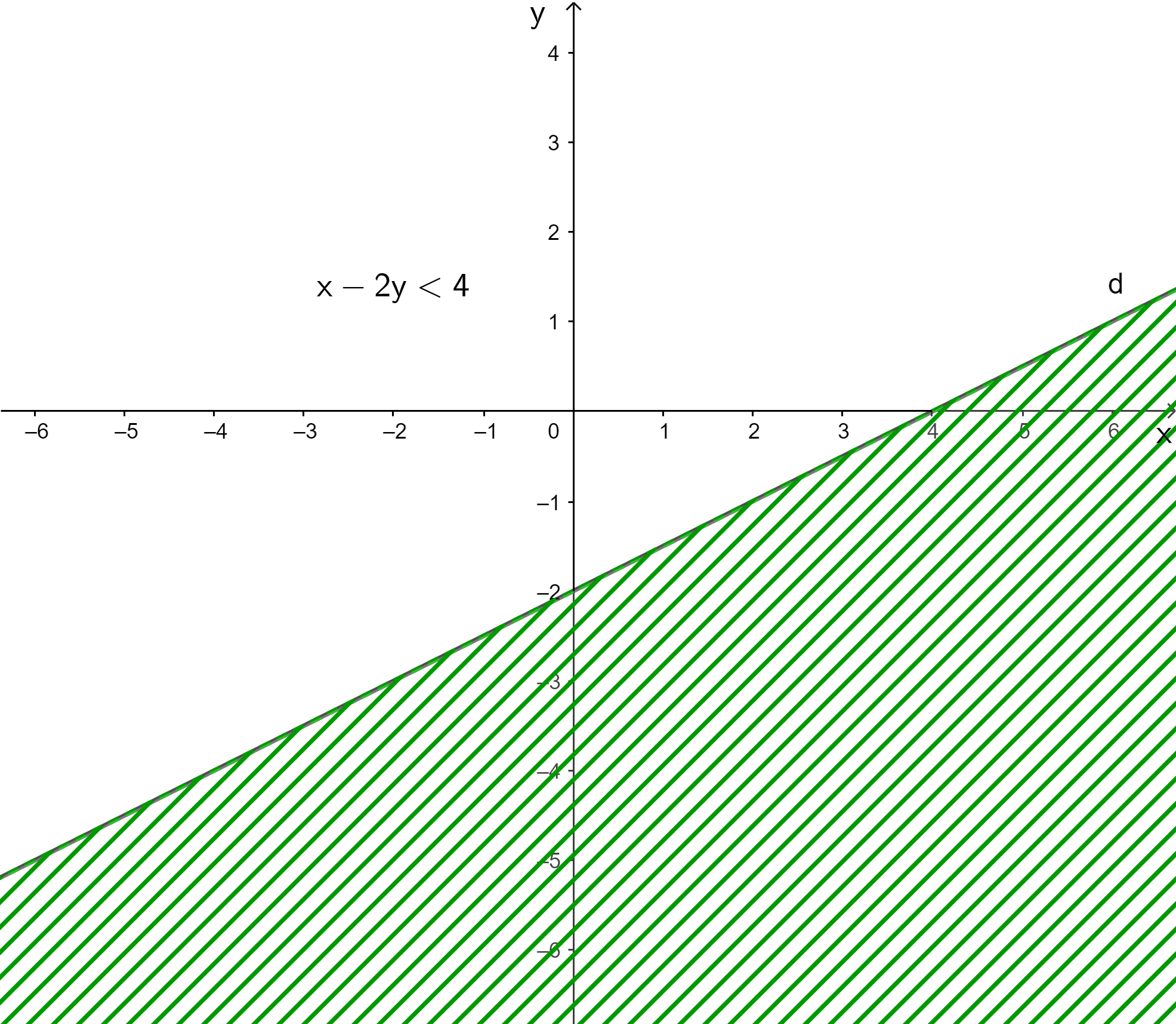
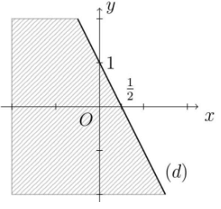
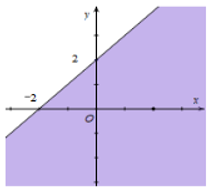
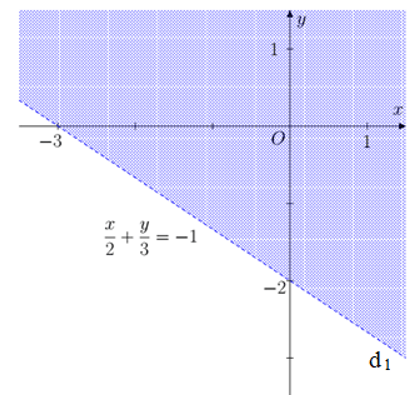
a) Vẽ đường thẳng d₁: $\frac{x}{3}+\frac{y}{2}=-1$.

Thay giá trị (0 ; 0) vào bất phương trình, ta có $\frac{0}{2}+\frac{0}{3}=0<-1$ là mệnh đề sai.

Miền nghiệm là miền không chứa điểm (0 ; 0), không kể đường thẳng d.

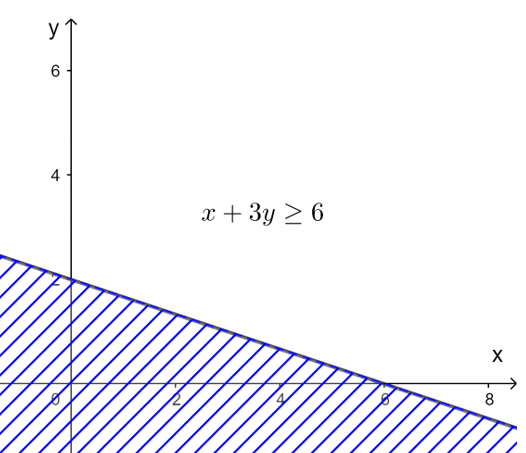
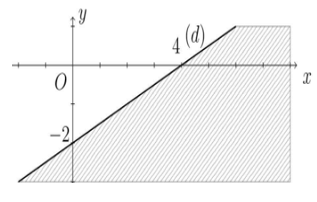
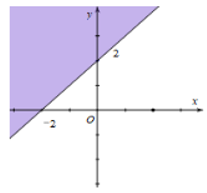
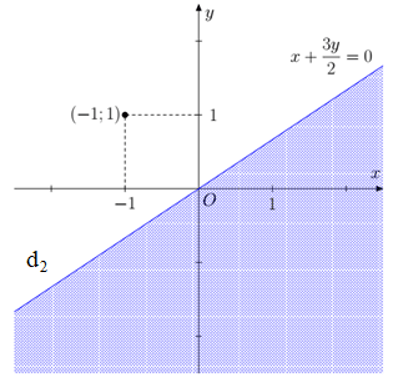
b) Vẽ đường thẳng d₂: $x-\frac{3y}{2}=0$.

Lấy điểm  (–1 ; 1). Ta có: $-1-\frac{3.1}{2}=-\frac{5}{2}\le 0$ là mệnh đề đúng.

Miền nghiệm là miền chứa điểm (–1 ; 1), kể cả đường thẳng d₂.

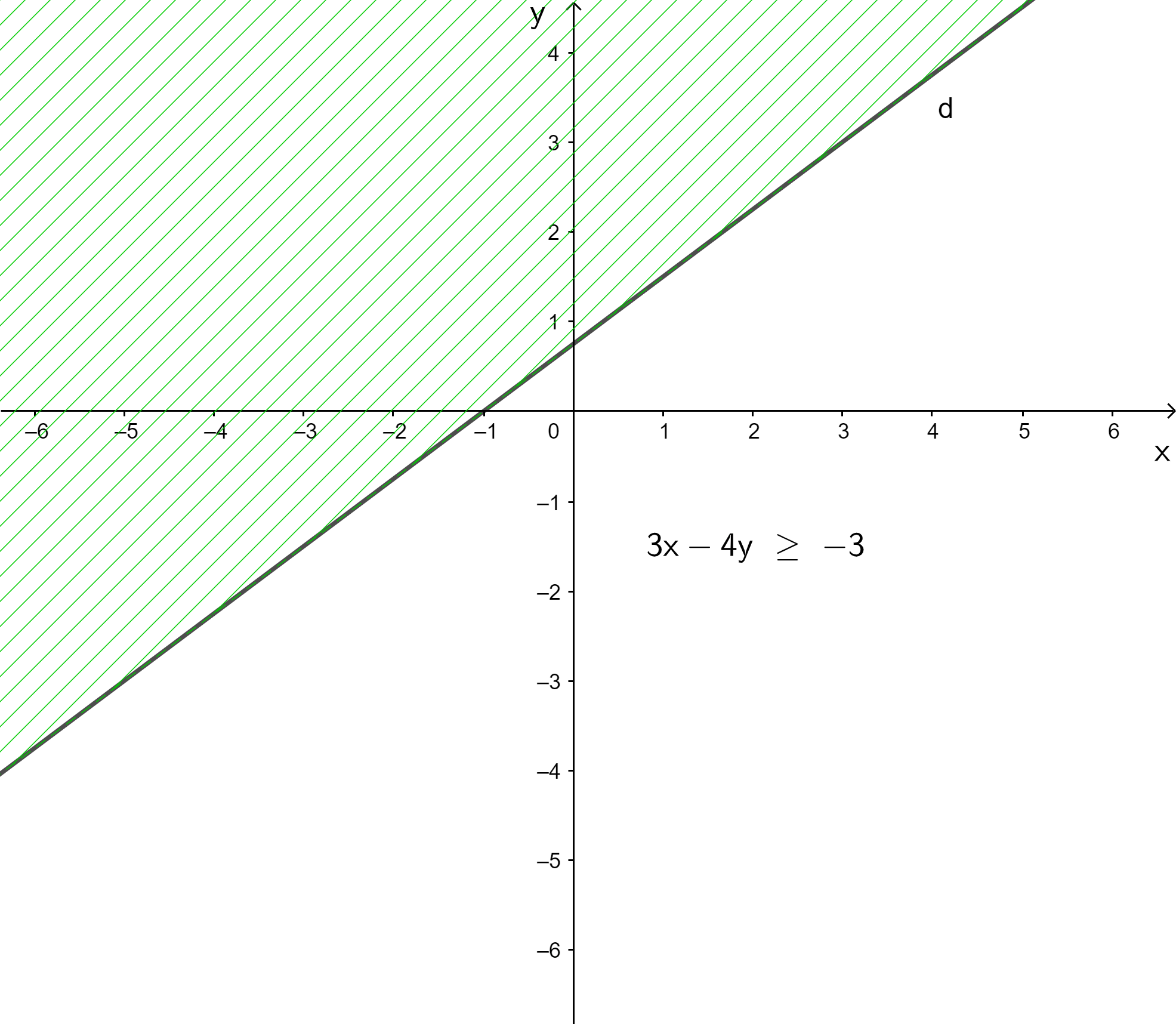
c)$\frac{x+y}{2}\ge \frac{2x-y+1}{3}$     

⇔ 3(x + y) ≥ 2(2x – y + 1)

⇔ 3x + 3y ≥ 4x – 2y + 2

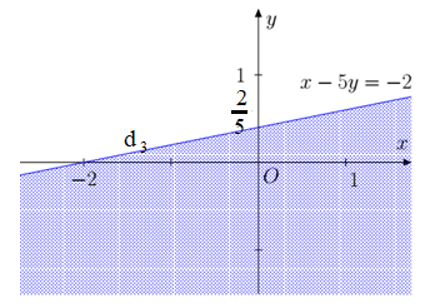
⇔ x – 5y ≤ –2

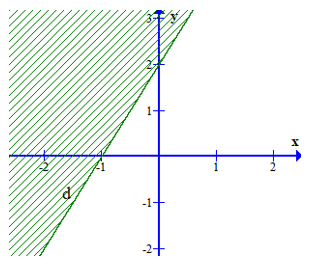
Vẽ đường thẳng d₃: x – 5y = –2.

Lấy điểm (0 ; 0). Ta có 0 – 0 = 0 ≤ –2 là mệnh đề sai.

Miền nghiệm là miền không chứa điểm (0 ; 0), kể cả đường thẳng d₃.

Bài 3. Một gian hàng trưng bày bàn và ghế rộng 60m². Diện tích để kê một chiếc ghế là 0,5m², một chiếc bàn là 1,2m². Gọi x là số ghế và y là số bàn được kê (x ≥ 0, y ≥ 0)

a) Viết bất phương trình bậc nhất hai ẩn x, y cho phần mặt sàn để kê bàn ghế.

b) Chỉ ra ba nghiệm của bất phương trình trên.

Hướng dẫn giải:

a) Diện tích kê x chiếc ghế và y chiếc bàn là 0,5x + 1,2y (m²).

Diện tích này không thể lớn hơn 60m² nên ta được bất phương trình cần tìm:

0,5x + 1,2y ≤ 60 hay 5x + 12y ≤ 600.

Vậy bất phương trình bậc nhất hai ẩn x, y cho phần mặt sàn để kê bàn ghế là: 5x + 12y ≤ 600.

b) Ví dụ về ba nghiệm của bất phương trình trên là các cặp giá trị (10 ; 10), (30; 15), (24; 40). Thật vậy:

Thay x = 10, y = 10, ta có: 5 . 10 + 12 . 10 = 170 ≤ 600 là mệnh đề đúng. Do đó (10; 10) là nghiệm của bất phương trình.

Thay x = 30, y = 15, ta có: 5 . 30 + 12 . 15 = 330 ≤ 600 là mệnh đề đúng. Do đó (30; 15) là nghiệm của bất phương trình.

Thay x = 24, y = 40, ta có: 5 . 24 + 12 . 40 = 600 ≤ 600 là mệnh đề đúng. Do đó (24; 40) là nghiệm của bất phương trình.

Vậy (10 ; 10), (30; 15), (24; 40) là ba nghiệm của bất phương trình 5x + 12y ≤ 600.

Học tốt Bất phương trình bậc nhất hai ẩn

Các bài học để học tốt Bất phương trình bậc nhất hai ẩn Toán lớp 10 hay khác:

15 Bài tập Bất phương trình bậc nhất hai ẩn (có đáp án) - Cánh diều Trắc nghiệm Toán 10

Với 15 bài tập trắc nghiệm Bất phương trình bậc nhất hai ẩn Toán lớp 10 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Cánh diều sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.

15 Bài tập Bất phương trình bậc nhất hai ẩn (có đáp án) - Cánh diều Trắc nghiệm Toán 10

Câu 1. Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình

2x  + y < 1

A. (– 2; 1);

B. (3; – 7);

C. (0; 1);

D. (0; 0).

Câu 2. Cặp số (1; – 1) là nghiệm của bất phương trình nào sau đây?

A. x + y  – 3 > 0;

B. – x – y < 0;

C. x + 3y + 1 < 0;

D. – x – 3y – 1 < 0.

Câu 3. Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình

x – 4y + 5 ≥ 0

A. (– 5; 0);

B. (– 2; 1);

C. (1; – 3);

D. (0; 0).

Câu 4. Cặp số nào sau đây là nghiệm của bất phương trình – 2(x – y) + y > 3?

A. (4; – 4);

B. (2; 1);

C. (– 1; – 2);

D. (4; 4).

Câu 5. Bất phương trình 3x – 2(y – x + 1) > 0 tương đương với bất phương trình nào sau đây?

A. x – 2y – 2 > 0;

B. 5x – 2y – 2 > 0;

C. 5x – 2y – 1 > 0;

D. 4x – 2y – 2 > 0.

Câu 6. Nửa mặt phẳng là miền nghiệm của bất phương trình – x + 2 + 2(y – 2) < 2(1 – x) không chứa điểm nào trong các điểm sau:

A. (0; 0);

B. (1; 1);     

C. (4; 2);

D. (1; – 1).

Câu 7. Phần tô đậm trong hình vẽ dưới đây (kể cả đường thẳng d) biểu diễn miền nghiệm của bất phương trình.

A. – 2x + y ≥ 0;

B. 2x + y ≥ 0;

C. – 2x – y ≥ 1;

D. x + 2y ≥ 0.

Câu 8. Phần nửa mặt phẳng tô đậm (không kể đường thẳng ∆) trong hình vẽ dưới đây biểu diễn miền nghiệm của bất phương trình nào?

A. x + y > 2;

B. x – 2 y > 2;

C. x + y > – 2;

D. x – 2y > – 2.

Câu 9. Phần nữa mặt phẳng không bị gạch (không kể đường thẳng d) ở hình dưới đây là miền nghiệm của bất phương trình nào?

A. – x + 2y > 2;

B. 2x – y > – 4;

C. 2x – y > 2;

D. – x + 2y > – 4.

Câu 10. Phần nữa mặt phẳng không bị gạch (không kể đường thẳng d) ở hình dưới đây là miền nghiệm của bất phương trình nào?

A. 2x + y > 1;

B. 2x + y > – 1;

C. x + 2y > 1;

D. x + 2y > – 1.

Câu 11. Miền nghiệm của bất phương trình x + y ≤ 2 là phần tô đậm của hình vẽ nào, trong các hình vẽ sau (kể cả bờ)?

A.

B.

C.

D.

Câu 12. Cho bất phương trình 3x + 2 + 2(y – 2) < 2(x + 1) miền nghiệm của bất phương trình không chứa điểm nào sau đây?

A. (0; 0);

B. (1; 1);

C. (1; – 1);

D. (4; 2).

Câu 13. Cặp số (1; – 1) là nghiệm của bất phương trình nào sau đây?

A. x + y – 3 > 0;

B. – x – y  < 0;

C. x + 3y + 1< 0;  

D. – x – 3y – 1 < 0.

Câu 14. Cặp số nào sau đây không là nghiệm của bất phương trình 5x – 2(y – 1) ≤ 0?

A. (0; 1) ;

B. (1 ; 3);

C. (– 1; 1);

D. (– 1; 0).

Câu 15. Phần nữa mặt phẳng không bị gạch (không kể đường thẳng d) ở hình dưới đây là miền nghiệm của bất phương trình nào?

A. 2x –  y > – 2;

B. 2x + y > – 2;

C. x + 2y > 2;

D. x + 2y > – 2.

Xem thêm bài tập trắc nghiệm Toán lớp 10 Cánh diều có đáp án hay khác: