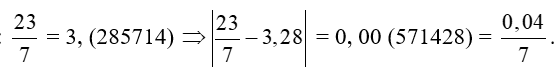Với giải bài tập Toán 10 Bài 1: Số gần đúng. Sai số sách Cánh diều hay nhất, chi tiết giúp học sinh lớp 10 dễ dàng làm bài tập Toán 10 Bài 1.

Giải Toán 10 Cánh diều Bài 1: Số gần đúng. Sai số

Câu hỏi khởi động

Giải Toán 10 trang 21 Tập 2

Câu hỏi khởi động trang 21 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 1: Số gần đúng. Sai số

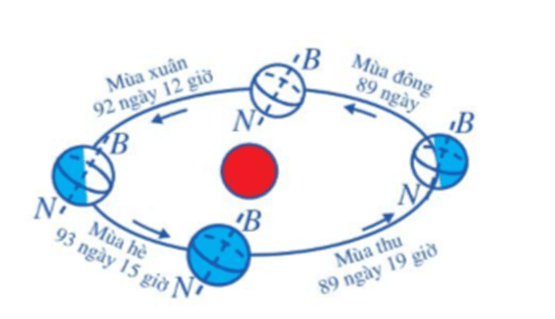
Câu hỏi khởi động trang 21 Toán lớp 10 Tập 2: Trái Đất với tên gọi “Hành tinh xanh” là ngôi nhà chung của nhân loại. Trong Hệ Mặt Trời, Trái Đất là hành tinh thứ ba tính từ Mặt Trời, đồng thời cũng là hành tinh lớn nhất trong các hành tinh đất đá xét về bán kính, khối lượng và mật độ vật chất.

Trái Đất có diện tích toàn bộ bề mặt là 510,072 triệu km².

(Nguồn: https://vi.wikipedia.org)

Con số 510,072 (triệu km²) là số chính xác hay số gần đúng?

Lời giải:

Con số 510,072 (triệu km²) là một số gần đúng vì ta không thể đo đạc được chính xác diện tích toàn bộ bề mặt Trái Đất.

Lời giải Toán 10 Bài 1: Số gần đúng. Sai số hay, chi tiết khác:

Hoạt động 1 trang 21 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 1: Số gần đúng. Sai số

Hoạt động 1 trang 21 Toán lớp 10 Tập 2: Hóa đơn tiền điện tháng 4/2021 của gia đình bác Mai là 763 951 đồng. Trong thực tế, bác Mai đã thanh toán (hóa đơn) bằng tiền mặt cho người thu tiền điện số tiền là 764 000 đồng. Tại sao bác Mai không thể thanh toán bằng tiền mặt cho người thu tiền điện số tiền chính xác là 763 951 đồng?

Lời giải:

Bác Mai không thể thanh toán bằng tiền mặt cho người thu tiền điện số tiền chính xác là 763 951 đồng vì tiền mặt của Việt Nam không có các đồng tiền có mệnh giá 1 đồng, 50 đồng và 900 đồng, do đó sử dụng tiền giấy để thanh toán thì không có các tờ tiền để tổng số tiền là 763 951 đồng.

Lời giải Toán 10 Bài 1: Số gần đúng. Sai số hay, chi tiết khác:

Hoạt động 2 trang 22 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 1: Số gần đúng. Sai số

Hoạt động 2 trang 22 Toán lớp 10 Tập 2: Một bồn hoa có dạng hình tròn với bán kính là 0,8 m

a) Viết công thức tính diện tích S của bồn hoa theo π và bán kính 0,8 m.

b) Khi tính diện tích của bồn hoa, bạn Ngân lấy một giá trị gần đúng của π là 3,1 và được kết quả là:

3,1 . (0,8)2 = 1,984 (m2).

Giá trị |S – 1,984| biểu diễn điều gì?

Lời giải:

a) Vì bồn hoa có dạng hình tròn với bán kính 0,8 m nên diện tích bồn hoa là:

S = π . (0,8)² = 0,64π (m²).

b) Ta có 1,984 là giá trị gần đúng của diện tích S của bồn hoa.

Do đó giá trị |S – 1,984| chính là khoảng chênh lệch của diện tích đúng của bồn hoa và diện tích gần đúng của bồn hoa. Ta gọi giá trị này là sai số tuyệt đối của số gần đúng 1,984.

Lời giải Toán 10 Bài 1: Số gần đúng. Sai số hay, chi tiết khác:

Hoạt động 3 trang 23 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 1: Số gần đúng. Sai số

Hoạt động 3 trang 23 Toán lớp 10 Tập 2: Hãy ước lượng sai số tuyệt đối ${\Delta }_{S_1}$ ở Ví dụ 1.

Lời giải:

Để ước lượng sai số tuyệt đối trên, ta làm như sau:

Do 3,1 < π < 3,15 nên 3,1 . (0,8)² < π . (0,8)² < 3,15 . (0,8)².

Suy ra 1,984 < S < 2,016.

Vậy ${\Delta }_{S_1}=\left(S-S_1\right)<2,016-1,984=0,032$.

Ta nói: Kết quả của bạn Ngân có sai số tuyệt đối không vượt quá 0,032 hay có độ chính xác là 0,032.

Lời giải Toán 10 Bài 1: Số gần đúng. Sai số hay, chi tiết khác:

Hoạt động 4 trang 23 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 1: Số gần đúng. Sai số

Hoạt động 4 trang 23 Toán lớp 10 Tập 2: Các nhà thiên văn tính được thời gian để Trái Đất quay một vòng quanh Mặt Trời là 365 ngày $\pm \frac{1}{4}$ ngày. Bạn Hùng tính thời gian đi bộ một vòng quanh sân vận động của trường khoảng 15 phút ± 1 phút. Trong hai phép đo trên, phép đo nào chính xác hơn?

Lời giải:

Phép đo của các nhà thiên văn có sai số tuyệt đối không vượt quá $\frac{1}{4}$ ngày, có nghĩa là không vượt quá 360 phút. Phép đo của Hùng có sai số tuyệt đối không quá 1 phút. Nếu chỉ so sánh 360 phút và 1 phút thì có thể dẫn đến hiểu rằng phép đo của bạn Hùng chính xác hơn phép đo của các nhà thiên văn. Tuy nhiên, $\frac{1}{4}$ ngày hay 360 phút là độ chính xác của phép đo một chuyển động trong 365 ngày, còn 1 phút là độ chính xác của phép đo một chuyển động trong 15 phút. So sánh hai tỉ số $\frac{\frac{1}{4}}{365}=\frac{1}{1460}=0,\mathrm{0006849...}$ và $\frac{1}{15}=0,\mathrm{0666....}$, ta thấy rằng phép đo của các nhà thiên văn chính xác hơn nhiều.

Lời giải Toán 10 Bài 1: Số gần đúng. Sai số hay, chi tiết khác:

Hoạt động 5 trang 25 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 1: Số gần đúng. Sai số

Hoạt động 5 trang 25 Toán lớp 10 Tập 2: Quy tròn số 3,141 đến hàng phần trăm rồi tính sai số tuyệt đối của số quy tròn.

Lời giải:

Quy tròn số 3,141 đến hàng phần trăm ta được số 3,14.

Sai số tuyệt đối của số quy tròn là ∆ = |3,141 – 3,14| = 0,001 < 0,005. Do vậy, số quy tròn 3,14 là số gần đúng của số 3,141 với độ chính xác 0,005.

Lời giải Toán 10 Bài 1: Số gần đúng. Sai số hay, chi tiết khác:

Hoạt động 6 trang 25 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 1: Số gần đúng. Sai số

Hoạt động 6 trang 25 Toán lớp 10 Tập 2: Cho số gần đúng a = 1,2345 với độ chính xác 0,005. Hãy đọc hai yêu cầu sau và cho biết hai yêu cầu đó khác nhau như thế nào:

a) Quy tròn số gần đúng a = 1,2345 đến hàng phần trăm;

b) Quy tròn số gần đúng a = 1,2345.

Lời giải:

Yêu cầu ở câu a) Đề bài đã cho rõ hàng quy tròn, ta chỉ cần quy tròn số a = 1,2345 đến hàng phần trăm.

Yêu cầu ở câu b) Đề bài chưa cho hàng quy tròn, ta cần xem xét độ chính xác, từ đó mới biết được hàng quy tròn để quy tròn số gần đúng a = 1,2345.

Lời giải Toán 10 Bài 1: Số gần đúng. Sai số hay, chi tiết khác:

Luyện tập 1 trang 25 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 1: Số gần đúng. Sai số

Luyện tập 1 trang 25 Toán lớp 10 Tập 2: Hãy viết số quy tròn của số gần đúng a = 28,4156 biết $\overline{a}=28,4156\pm 0,0001$.

Lời giải:

Vì $\overline{a}=28,4156\pm 0,0001$ nên độ chính xác d = 0,0001.

Do 0,00001 < d = 0,0001 < 0,001 nên hàng thấp nhất mà d nhỏ hơn một đơn vị của hàng đó là hàng phần nghìn. Vì thế, ta quy tròn số a đến hàng phần nghìn theo quy tắc quy tròn.

Vậy số quy tròn của a là 28,416.

Lời giải Toán 10 Bài 1: Số gần đúng. Sai số hay, chi tiết khác:

Hoạt động 7 trang 26 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 1: Số gần đúng. Sai số

Hoạt động 7 trang 26 Toán lớp 10 Tập 2: Như đã biết, nếu số đúng là số nguyên hoặc số thập phân thì ta có thể tìm dễ dàng số gần đúng với độ chính xác cho trước bằng cách quy tròn về hàng thích hợp. Tuy nhiên, việc biểu diễn số thực về dạng số nguyên hoặc số thập phân trong thực tiễn là không đơn giản. Ngày nay, ta có thể sử dụng máy tính cầm tay hoặc các phương tiện tính toán hiện đại để giải quyết vấn đề đó.

Sử dụng máy tính cầm tay, tính $3^7.\sqrt{14}$ (trong kết quả lấy bốn chữ số ở phần thập phân).

Lời giải:

Để thực hiện phép tính trên ra kết quả có bốn chữ số ở phần thập phân, ta có thể làm như sau:

Lời giải Toán 10 Bài 1: Số gần đúng. Sai số hay, chi tiết khác:

Luyện tập 2 trang 26 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 1: Số gần đúng. Sai số

Luyện tập 2 trang 26 Toán lớp 10 Tập 2: Sử dụng máy tính cầm tay, tính

Lời giải:

Để thực hiện phép tính trên ra kết quả có hai chữ số ở phần thập phân, ta có thể làm như sau:

Lời giải Toán 10 Bài 1: Số gần đúng. Sai số hay, chi tiết khác:

Luyện tập 3 trang 26 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 1: Số gần đúng. Sai số

Luyện tập 3 trang 26 Toán lớp 10 Tập 2: Hãy tìm hiểu khối lượng của Trái Đất, Mặt Trời và viết kết quả dưới dạng số gần đúng

Lời giải:

Theo https://vi.wikipedia.org:

+ Khối lượng của Trái Đất khoảng 5,9722 × 10²⁴ (kg).

+ Khối lượng của Mặt Trời là (1,98855 ± 0,00025) × 10³⁰ kg.

Lời giải Toán 10 Bài 1: Số gần đúng. Sai số hay, chi tiết khác:

Bài 1 trang 26 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 1: Số gần đúng. Sai số

Bài 1 trang 26 Toán lớp 10 Tập 2: Quy tròn số – 3,2475 đến hàng phần trăm. Số gần đúng nhận được có độ chính xác là bao nhiêu?

Lời giải:

Quy tròn số – 3,2475 đến hàng phần trăm ta được – 3,25.

Sai số tuyệt đối là ∆ = |– 3,2475 – (– 3,25)| = 0,0025 < 0,005.

Vậy số gần đúng – 3,25 có độ chính xác là d = 0,005.

(Ta có thể tìm độ chính xác bằng cách lấy nửa đơn vị của hàng quy tròn).

Lời giải Toán 10 Bài 1: Số gần đúng. Sai số hay, chi tiết khác:

Bài 2 trang 26 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 1: Số gần đúng. Sai số

Bài 2 trang 26 Toán lớp 10 Tập 2: Viết số quy tròn của mỗi số gần đúng sau với độ chính xác d:

Lời giải:

Theo https://vi.wikipedia.org:

+ Khối lượng của Trái Đất khoảng 5,9722 × 10²⁴ (kg).

+ Khối lượng của Mặt Trời là (1,98855 ± 0,00025) × 10³⁰ kg.

Lời giải Toán 10 Bài 1: Số gần đúng. Sai số hay, chi tiết khác:

Bài 3 trang 26 Toán 10 Tập 2 Cánh diều

Giải Toán 10 Cánh diều Bài 1: Số gần đúng. Sai số

Bài 3 trang 26 Toán lớp 10 Tập 2: Ta đã biết 1 inch (kí hiệu là in) là 2,54 cm. Màn hình của một chiếc ti vi có dạng hình chữ nhật với độ dài đường chéo là 32 in, tỉ số giữa chiều dài và chiều rộng của màn hình là 16 : 9. Tìm một giá trị gần đúng (theo đơn vị inch) của chiều dài màn hình ti vi và tìm sai số tương đối, độ chính xác của số gần đúng đó.

Lời giải:

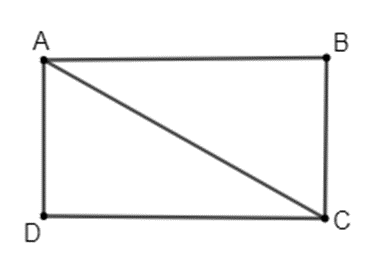
Ta mô phỏng màn hình ti vi có hình chữ nhật ABCD như sau:

Ta có: AC = 32 in, AB là chiều dài, BC là chiều rộng với AB : BC = 16 : 9.

Gọi chiều dài của ti vi là x (in, x > 0) hay AB = x, khi đó chiều rộng của ti vi là $BC=\frac{9}{16}x$

Sử dụng định lí Pythagore, ta có phương trình: $x^2+{\left(\frac{9}{16}x\right)}^2={32}^2$ (*).

Giải phương trình (*), ta có:

(*) $\iff x^2+\frac{81}{256}{x}^2=1024\iff \frac{337}{256}{x}^2=1024\iff x^2=\frac{262144}{337}$

Do x > 0 nên x = $\frac{512}{\sqrt{337}}$.

Vậy chiều dài của chiếc ti vi là $\frac{512}{\sqrt{337}}=27,\mathrm{89041719...}$ (in).

Quy tròn số $\frac{512}{\sqrt{337}}$ đến hàng phần trăm được 27,89.

Ta có độ chính xác d = 0,005 (nửa đơn vị hàng quy tròn).

Vậy sai số tương đối ${\delta }_a\le \frac{0,005}{27,89}\approx 0,02\%$.

Lời giải Toán 10 Bài 1: Số gần đúng. Sai số hay, chi tiết khác:

Sách bài tập Toán 10 Bài 1: Số gần đúng. Sai số - Cánh diều

Với giải sách bài tập Toán 10 Bài 1: Số gần đúng. Sai số sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 Bài 1.

Sách bài tập Toán 10 Bài 1: Số gần đúng. Sai số - Cánh diều

Giải SBT Toán 10 trang 27 Tập 2

Số gần đúng. Sai số (Lý thuyết Toán lớp 10) - Cánh diều

Với tóm tắt lý thuyết Toán 10 Bài 1: Số gần đúng. Sai số sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.

Số gần đúng. Sai số (Lý thuyết Toán lớp 10) - Cánh diều

Lý thuyết Số gần đúng. Sai số

I. Số gần đúng

Trong đo đạc và tính toán, ta thường chỉ nhận được các số gần đúng.

Ví dụ: Dân số Việt Nam năm 2017 ước tính là 93,7 triệu người. Khi đó con số 93,7 triệu người là số gần đúng.

II. Sai số của số gần đúng

1. Sai số tuyệt đối

Nếu a là số gần đúng của số đúng $\overline{a}$ thì ∆_a = |$\overline{a}$ - a| được gọi là sai số tuyệt đối của số gần đúng a (Hình vẽ).

Chú ý: Sai số tuyệt đối của số gần đúng nhận được trong một phép đo đạc, tính toán càng bé thì kết quả của phép đo đạc, tính toán đó càng chính xác.

Ví dụ: Hai bạn Nam và Long muốn tính chu vi của một đường tròn có bán kính 1 cm. Bạn Nam lấy π là 3,14 còn Long lấy π là 3,1. Hỏi kết quả của bạn nào chính xác hơn.

Hướng dẫn giải

Gọi chu vi đường tròn bán kính r = 1 cm là C = 2πr (cm).

Bạn Nam tính được chu vi của đường tròn khi lấy π = 3,14 là:

C₁ = 2πr = 2.3,14.1 = 6,28 (cm).

Bạn Long tính được chu vi của đường tròn khi lấy π = 3,1 là:

C₂ = 2πr = 2.3,1.1 = 6,2 (cm).

Ta thấy 3,1 < 3,14 < π nên 2.3,1.1 < 2.3,14.1 < 2.π.1

Tức là C₂ < C₁ < C.

Suy ra ${∆}_{c_1}=|C-C_1|<|C-C_2|={∆}_{c_2}$.

⇒ ${∆}_{c_1}<{∆}_{c_2}$.

⇒ Kết quả của bạn Nam chính xác hơn kết quả của bạn Long.

Vậy kết quả tính chu vi đường tròn của bạn Nam chính xác hơn kết quả của bạn Long.

2. Độ chính xác của một số gần đúng

Nhận xét:

- Giả sử a là số gần đúng của số đúng $\overline{a}$ sao cho ∆_a = |$\overline{a}$ - a| ≤ d.

Khi đó ∆_a = |$\overline{a}$ - a| ≤ d⇔ –d ≤ $\overline{a}$ - a ≤ d ⇔ a – d ≤ $\overline{a}$ ≤ a + d.

- Ta nói a là số gần đúng của số đúng $\overline{a}$ với độ chính xác d nếu ∆_a = |$\overline{a}$ - a| ≤ d và quy ước viết gọn là $\overline{a}$ = a ± d.

- Nếu ∆_a ≤ d thì số đúng $\overline{a}$ nằm trong đoạn [a – d; a + d]. Bởi vậy, d càng nhỏ thì độ sai lệch của số gần đúng a so với số đúng $\overline{a}$ càng ít. Điều đó giải thích vì sao d được gọi là độ chính xác của số gần đúng.

Ví dụ: Tính độ chính xác của kết quả phép tính chu vi đường tròn bán kính 1 cm khi lấy π là 3,14.

Hướng dẫn giải

Khi lấy π là 3,14 ta có chu vi đường tròn bán kính r = 1 cm là

C₁ = 2.3,14.1 = 6,28 (cm).

Vì 3,14 < π < 3,15 nên 2.3,14.1 < 2π.1 < 2.3,15.1

⇒ 6,28 < C < 6,3

${∆}_{c_1}$ = |C – 6,28| < 6,3 – 6,28 = 0,02.

Vậy độ chính xác của phép tính này là 0,02.

3. Sai số tương đối

Tỉ số δ_a = $\frac{{∆}_a}{\left|a\right|}$ được gọi là sai số tương đối của số gần đúng a.

Nhận xét:

- Nếu $\overline{a}$ = a ± d thì ∆_a ≤ d. Do đó δ_a ≤ $\frac{d}{\left|a\right|}$. Vì vậy, nếu $\frac{d}{\left|a\right|}$ càng bé thì chất lượng của phép đo đạc, tính toán càng cao.

- Người ta thường viết sai số tương đối dưới dạng phần trăm.

Chẳng hạn, trong phép đo thời gian Trái Đất quay một vòng quanh Mặt Trời thì sai số tương đối không vượt quá $\frac{\frac{1}{4}}{365}=\frac{1}{1460}\approx 0,068\%$.

Ví dụ: Trong phép đo chiều dài của một đoạn đường thu được kết quả là 13,1 m với độ chính xác là 0,1 m. Hãy đánh giá sai số tương đối của số gần đúng này.

Hướng dẫn giải

Ta có số gần đúng a = 13,1 m và độ chính xác d = 0,1 m.

Do đó sai số tương đối là: δ_a ≤ $\frac{d}{\left|a\right|}$=$\frac{0,1}{13,1}\approx 0,76\%$.

Vậy sai số tương đối không vượt quá 0,76%.

III. Số quy tròn. Quy tròn số đúng và số gần đúng

1. Số quy tròn

Khi quy tròn một số nguyên hoặc một số thập phân đến một hàng nào đó thì số nhận được gọi là số quy tròn của số ban đầu.

Ví dụ: Quy tròn số 5,123 đến hàng phần trăm ta được số 5,12. Khi đó số 5,12 được gọi là số quy tròn của số 5,123.

2. Quy tròn số đến một hàng cho trước

Nhận xét: Khi quy tròn số nguyên hoặc số thập phân đến một hàng cho trước thì sai số tuyệt đối của số quy tròn không vượt quá nửa đơn vị của hàng quy tròn. Như vậy, ta có thể lấy độ chính xác của số quy tròn bằng nửa đơn vị của hàng quy tròn.

Ví dụ: Quy tròn số 2,516 đến hàng phần trăm rồi ước lượng độ chính xác của số đó.

Hướng dẫn giải

Quy tròn số 2,516 đến hàng phần trăm ta được số 2,52.

Sai số tuyệt đối là |2,516 – 2,52| = 0,004 < 0,005.

Vậy số quy tròn 2,52 là số gần đúng của 2,516 với độ chính xác 0,005.

3. Quy tròn số gần đúng căn cứ vào độ chính xác cho trước

Quy ước: Cho a là số gần đúng với độ chính xác d. Giả sử a là số nguyên hoặc số thập phân. Khi được yêu cầu quy tròn số a mà không nói rõ quy tròn đến hàng nào thì ta quy tròn a đến hàng thấp nhất mà d nhỏ hơn một đơn vị của hàng đó.

Ví dụ: Viết số quy tròn của số 1 348 với d = 300.

Hướng dẫn giải

Vì độ chính xác d = 300 thỏa mãn 100 < d = 300 < 1 000 nên hàng thấp nhất mà d nhỏ hơn một đơn vị của hàng đó là hàng nghìn.

Vì vậy, ta quy tròn số 1 348 đến hàng nghìn.

Quy tròn số 1 348 đến hàng nghìn ta được số 1 000.

Vậy số quy tròn của số 1 348 với độ chính xác d = 300 là 1 000.

Bài tập Số gần đúng. Sai số

Bài 1: Hãy quy tròn số – 2,17842 đến hàng phần nghìn. Số gần đúng nhận được có độ chính xác là bao nhiêu?

Hướng dẫn giải

Số quy tròn của số –2,17842 đến hàng phần nghìn là –2,178.

Ta có |–2,17842 – (–2,178)| = 0,00042 < 0,0005.

Vì vậy, độ chính xác d = 0,0005.

Vậy số quy tròn của số –2,17842 đến hàng phần nghìn là –2,178 và độ chính xác d = 0,0005.

Bài 2: Hãy viết số quy tròn của mỗi số gần đúng sau với độ chính xác d sau đó ước lượng sai số tương đối của số gần đúng đó.

a) a = 32 564 với d = 20;

b) a = 0,7612309 với d = 0,001.

Hướng dẫn giải

a) Vì độ chính xác d = 20 thỏa mãn 10 < d = 20 < 100 nên hàng thấp nhất mà d nhỏ hơn một đơn vị của hàng đó là hàng trăm.

Vì vậy, ta quy tròn số a = 32 564 đến hàng trăm.

Quy tròn số a = 32 564 đến hàng trăm ta được số quy tròn là 32 600.

Do đó sai số tương đối là: δ_a ≤ $\frac{d}{\left|a\right|}$= $\frac{20}{32564}\approx 0,06\%$.

Suy ra, sai số tương đối không vượt quá 0,06%.

Vậy số quy tròn của số gần đúng a = 32 564 với độ chính xác d = 20 là 32 600 và sai số tương đối không vượt quá 0,06%.

b) Vì độ chính xác d = 0,001 thỏa mãn d = 0,001 < 0,01 nên hàng thấp nhất mà d nhỏ hơn một đơn vị của hàng đó là hàng phần trăm.

Vì vậy, ta quy tròn số 0,7612309 đến hàng phần trăm.

Quy tròn số a = 0,7612309 đến hàng phần trăm ta được số quy tròn là 0,76.

Do đó sai số tương đối là: δ_a ≤ $\frac{d}{\left|a\right|}$= $\frac{0,001}{0,7612309}\approx 0,13\%$.

Suy ra, sai số tương đối không vượt quá 0,13%.

Vậy số quy tròn của số gần đúng a = 0,7612309 với độ chính xác d = 0,001 là 0,76 và sai số tương đối không vượt quá 0,13%.

Bài 3: Sử dụng máy tính cầm tay, tính và làm tròn kết quả của phép tính $\sqrt{15}:3-1$ (trong kết quả lấy ba chữ số ở phần thập phân).

Hướng dẫn giải

Để thực hiện phép tính $\sqrt{15}:3-1$ ra kết quả có ba chữ số ở phần thập phân, ta làm như sau :

Ta ấn liên tiếp

Tiếp tục ấn lần lượt phím thì màn hình hiện ra Fix 0 ~ 9?

Ấn tiếp ta thấy kết quả hiện ra là 0.291

Vậy kết quả làm tròn của $\sqrt{15}:3-1$ là 0,291.

Học tốt Số gần đúng. Sai số

Các bài học để học tốt Số gần đúng. Sai số Toán lớp 10 hay khác:

15 Bài tập Số gần đúng. Sai số (có đáp án) - Cánh diều Trắc nghiệm Toán 10

Với 15 bài tập trắc nghiệm Số gần đúng. Sai số Toán lớp 10 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Cánh diều sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.

15 Bài tập Số gần đúng. Sai số (có đáp án) - Cánh diều Trắc nghiệm Toán 10

Câu 1. Cho số gần đúng a = 23748023 với độ chính xác d = 101. Hãy viết số quy tròn của số a.

A. 23749000;

B. 23748000;

C. 23746000;

D. 23747000.

Câu 2. Cho giá trị gần đúng của π là a = 3, 141592653589 với độ chính xác ${10}^{-10}$. Hãy viết số quy tròn của số a.

A. a = 3,141592654;

B. a = 3,1415926536;

C. a = 3,141592653;

D. a = 3,1415926535.

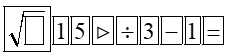
Câu 3.Sử dụng máy tính bỏ túi, hãy viết giá trị gần đúng của $\sqrt{3}$ chính xác đến hàng phần nghìn.

A. 1,7320;

B. 1,732;

C. 1,733;

D. 1,731.

Câu 4.Sử dụng máy tính bỏ túi, hãy viết giá trị gần đúng của ${\pi }^2$ chính xác đến hàng phần nghìn.

A. 9,873;

B. 9,870;

C. 9,872;

D. 9,871.

Câu 5. Hãy viết số quy tròn của số gần đúng a = 17658 biết $\overline{a}$ = 17658 ± 16.

A. 17700;

B. 17800;

C. 17500;

D. 17600.

Câu 6. Hãy viết số quy tròn của số gần đúng a = 15,318 biết $\overline{a}$ = 15,318 ± 0,056.

A. 15,3;

B. 15,31;

C. 15,32;

D. 15,4.

Câu 7. Đo độ cao một ngọn cây là h = 347,13m ± 0,2m. Hãy viết số quy tròn của số gần đúng 347,13.

A. 345;

B. 347;

C. 348;

D. 346.

Câu 8.Cho tam giác ABC có độ dài ba cạnh:

a = 12cm ± 0, 2cm;b = 10, 2cm ± 0, 2cm;c = 8cm ± 0,1cm. Tính chu vi P của tam giác đã cho.

A.P = 30, 2cm ± 0, 2cm;

B.P = 30, 2cm ± 1cm;

C.P = 30, 2cm ± 0, 5cm;

D.P = 30, 2cm ± 2cm.

Câu 9. Một miếng đất hình chữ nhật có chiều rộng x = 43m ± 0,5m và chiều dài

y = 63m ± 0,5m. Tính chu vi P của miếng đất đã cho.

A. P = 212m ± 4m;

B. P = 212m ± 2m;

C. P = 212m ± 0,5m;

D. P = 212m ± 1m.

Câu 10. Một thửa ruộng hình chữ nhật có chiều dài là x = 23m ± 0,01m và chiều rộng là y = 15m ± 0,01m. Tính diện tích S của thửa ruộng đã cho.

A. S = 345m ± 0, 001m;

B. S = 345m ± 0, 38m;

C. S = 345m ± 0, 01m;

D. S = 345m ± 0, 3801m.

Câu 11: Cho giá trị gần đúng của $\frac{23}{7}$ là 3,28. Sai số tuyệt đối của số 3,28 là:

A. 0,04;

B.$\frac{0,04}{7}$;

C. 0,06.

D. Đáp án khác.

Câu 12: Trong các thí nghiệm hằng số C được xác định là 5,73675 với cận trên sai số tuyệt đối là d = 0,00421. Viết chuẩn giá trị gần đúng của C là:

A. 5,74 ;

B. 5,736 ;

C. 5,737 ;

D. 5,7368.

Câu 13: Viết giá trị gần đúng của $\sqrt{10}$ đến hàng phần trăm (dùng MTBT):

A.3,16;

B.3,17;

C.3,10;

D.3,162.

Câu 14: Ký hiệu khoa học của số -0,000567 là:

A.-567.${10}^{-6}$;

B.-5,67.${10}^{-5}$;

C. -567.${10}^{-4}$;

D. -567.${10}^{-3}$.

Câu 15: Khi sử dụng máy tính bỏ túi với 10 chữ số thập phân ta được: $\sqrt{8}$= 2,828427125. Giá trị gần đúng của $\sqrt{8}$ chính xác đến hàng phần trăm là:

A. 2, 80;

B. 2, 81;

C. 2, 82;

D. 2, 83.

Xem thêm bài tập trắc nghiệm Toán lớp 10 Cánh diều có đáp án hay khác: