Với giải bài tập Toán 10 Bài 1: Quy tắc cộng và quy tắc nhân sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh lớp 10 dễ dàng làm bài tập Toán 10 Bài 1.

Giải Toán 10 Chân trời sáng tạo Bài 1: Quy tắc cộng và quy tắc nhân

Giải Toán 10 trang 20 Tập 2

Hoạt động khởi động trang 20 Toán 10 Tập 2 Chân trời sáng tạo

Giải Toán 10 Chân trời sáng tạo Bài 1: Quy tắc cộng và quy tắc nhân

Hoạt động khởi động trang 20 Toán lớp 10 Tập 2: Một công ty dự kiến tạo các mã số nhân viên, mỗi mã số có ba kí tự gồm một chữ cái tiếng Anh viết hoa đứng trước hai chữ số. Tuy nhiên, họ băn khoăn rằng số mã số như vậy có đủ để cấp cho mỗi nhân viên của họ một mã số riêng hay không. Họ cần làm gì để biết được điều đó?

Lời giải:

Sau bài học này ta có thể giải quyết bài toán trên như sau:

Bảng chữ cái tiếng Anh có tất cả 26 chữ cái;

Có tất cả 10 chữ số: 0; 1; 2; 3; 4; 5; 6; 7; 8; 9.

Công việc chọn mã số thẻ cho nhận viên như trên có thể coi gồm hai công đoạn:

- Công đoạn thứ nhất: Chọn một chữ cái từ 26 chữ cái có 26 cách;

- Công đoạn thứ hai: Ứng với mỗi cách chọn một chữ cái, có 10 cách chọn một chữ số ở giữa.

- Công đoạn thứ ba: Ứng với mỗi cách chọn một chữ cái và một chữ số đằng trước, có 10 cách chọn cho chữ số cuối cùng.

Theo quy tắc nhân, có: 26.10.10 = 2 600 cách tạo mã số thẻ cho nhân viên.

Nếu như số lượng nhân viên của công ty đó nhỏ hơn hoặc bằng 2 600 thì hoàn toàn có thể cấp đủ mã thẻ cho từng nhân viên, còn nếu số lượng nhân viên của công ty lơn hơn 2 600 thì không đủ mã thẻ cấp cho từng nhân viên.

Lời giải bài tập Toán 10 Bài 1: Quy tắc cộng và quy tắc nhân hay, chi tiết khác:

Hoạt động khám phá 1 trang 20 Toán 10 Tập 2 Chân trời sáng tạo

Giải Toán 10 Chân trời sáng tạo Bài 1: Quy tắc cộng và quy tắc nhân

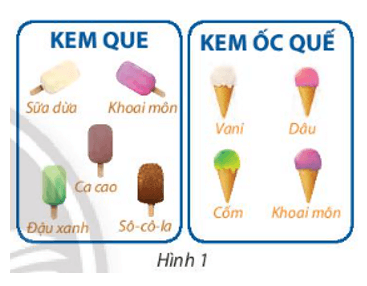
Hoạt động khám phá 1 trang 20 Toán lớp 10 Tập 2: Trong một cửa hàng kem có 5 loại kem que và 4 loại kem ốc quế như Hình 1. Có bao nhiêu cách chọn mua một loại kem que hoặc kem ốc quế ở cửa hàng này?

Lời giải:

Trong hoạt động trên, việc mua kem có thể có hai phương án một là mua kem que, hai là mua kem ốc quế. Đối với phương án mua kem que thì có tất cả 5 lựa chọn hay chính là 5 cách mua kem que. Phương án mua kem ốc quế thì có tất cả 4 lựa chon hay có 4 cách mua kem ốc quế. Số cách chọn mua một loại kem que hoặc kem ốc quế ở cửa hàng này là tổng số cách của hai phương án trên nên ta có tổng số cách là 5 + 4 = 9 cách.

Vậy có tất cả 9 cách để mua một loại kem que hoặc kem ốc quế ở cửa hàng này.

Lời giải bài tập Toán 10 Bài 1: Quy tắc cộng và quy tắc nhân hay, chi tiết khác:

Thực hành 1 trang 21 Toán 10 Tập 2 Chân trời sáng tạo

Giải Toán 10 Chân trời sáng tạo Bài 1: Quy tắc cộng và quy tắc nhân

Thực hành 1 trang 21 Toán lớp 10 Tập 2: Hà có 5 cuốn sách khoa học, 4 cuốn tiểu thuyết và 3 cuốn truyện tranh (các sách khác nhau từng đôi một). Hà đồng ý cho Nam mượn một cuốn sách trong số đó để đọc. Nam có bao nhiêu cách chọn một cuốn sách để mượn.

Lời giải:

Nam có ba phương án để mượn sách:

Phương án 1: Mượn sách khoa học, có 5 cách lựa chọn.

Phương án 2: Mượn tiểu thuyết, có 4 cách lựa chọn.

Phương án 3: Mượn truyện tranh, có 3 cách lựa chọn.

Áp dụng quy tắc cộng, ta có số cách để Nam mượn sách là:

5 + 4 + 3 = 12 (cách).

Vậy Nam có tất cả 12 cách để mượn sách.

Lời giải bài tập Toán 10 Bài 1: Quy tắc cộng và quy tắc nhân hay, chi tiết khác:

Hoạt động khám phá 2 trang 21 Toán 10 Tập 2 Chân trời sáng tạo

Giải Toán 10 Chân trời sáng tạo Bài 1: Quy tắc cộng và quy tắc nhân

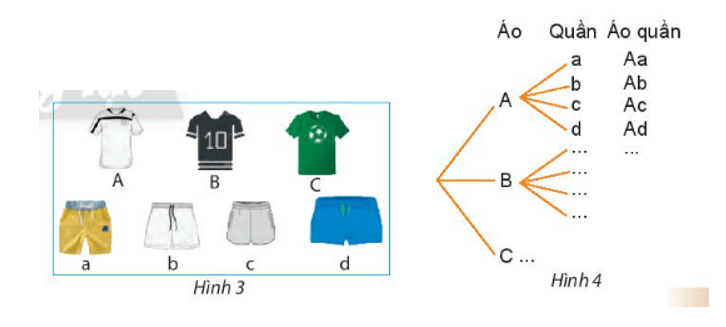
Hoạt động khám phá 2 trang 21 Toán lớp 10 Tập 2: An có 3 chiếc áo và 4 chiếc quần thể thao. An muốn chọn một bộ quần áo trong số đó để mặc chơi thể thao cuối tuần này.

a) Vẽ vào vở và hoàn thành sơ đồ hình cây như Hình 4 để thể hiện tất cả các khả năng mà An có thể lựa chọn một bộ quần áo.

b) An có bao nhiêu cách lựa chọn bộ quần áo? Hãy giải thích.

Lời giải:

a) Ta có sơ đồ sau:

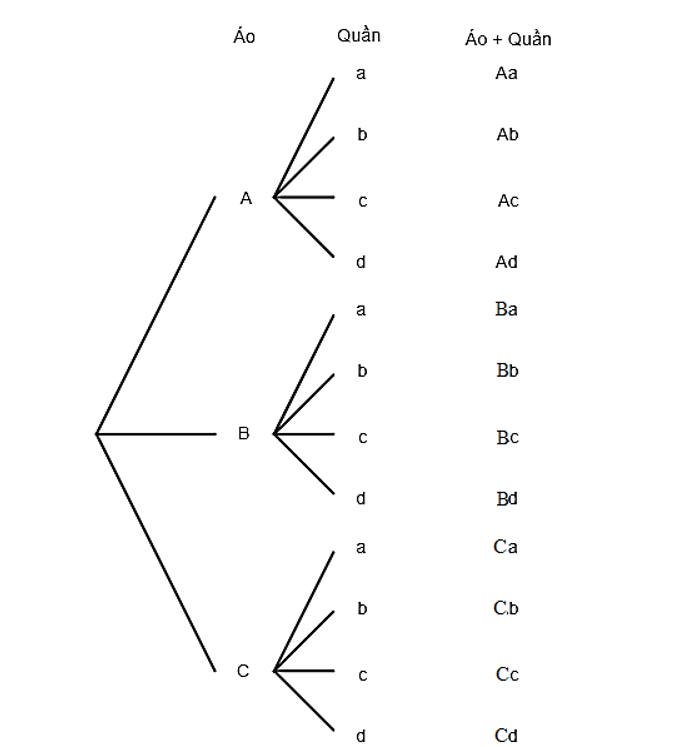
b) Công việc lựa chọn quần áo của bạn An ở trên có hai công đoạn:

Công đoạn thứ nhất: Chọn một chiếc áo từ ba chiếc áo A, B, C. Có 3 cách thực hiện.

Công đoạn thứ hai: Ứng với mỗi cách chọn một chiếc áo, có 4 cách chọn quần.

Theo sơ đồ ta thấy An có tất cả 12 cách chọn bộ quần áo hay là tích của số cách thực hiện hai công đoạn trên.

Lời giải bài tập Toán 10 Bài 1: Quy tắc cộng và quy tắc nhân hay, chi tiết khác:

Thực hành 2 trang 24 Toán 10 Tập 2 Chân trời sáng tạo

Giải Toán 10 Chân trời sáng tạo Bài 1: Quy tắc cộng và quy tắc nhân

Thực hành 2 trang 24 Toán lớp 10 Tập 2: Một mẫu xe ô tô có 4 màu ngoại thất là trắng, đen, cam và bạc. Mẫu xe này cũng có hai màu nội thất là đen và xám.

a) Khách hành có bao nhiêu lựa chọn về màu ngoại thất và nội thất khi mua một chiếc xe mẫu này?

b) Hãy vẽ sơ đồ hình cây để giải thích cho kết quả tính toán ở trên.

Lời giải:

a) Việc mua xe được chia làm hai công đoạn:

Công đoạn thứ nhất: Chọn màu ngoại thất, có 4 cách chọn.

Công đoạn thứ hai: Ứng với mỗi màu ngoại thất, có 2 cách chọn màu nội thất.

Theo quy tắc nhân, có 4.2 = 8 cách chọn mua một chiếc xe.

b) Ta có sơ đồ cây sau:

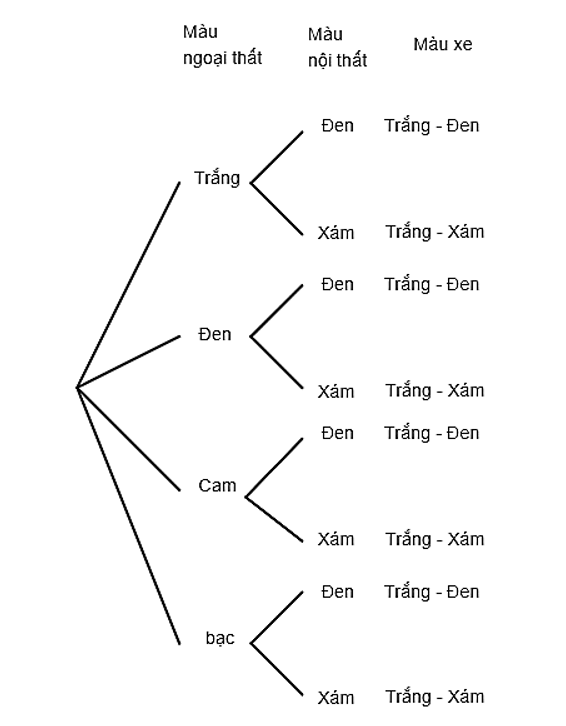
Lời giải bài tập Toán 10 Bài 1: Quy tắc cộng và quy tắc nhân hay, chi tiết khác:

Thực hành 3 trang 24 Toán 10 Tập 2 Chân trời sáng tạo

Giải Toán 10 Chân trời sáng tạo Bài 1: Quy tắc cộng và quy tắc nhân

Thực hành 3 trang 24 Toán lớp 10 Tập 2: Có nhiều nhất bao nhiêu đoạn phân tử RNA khác nhau chứa 4 phân tử nucleotide trong đó:

a) không có nucleotide A nào?

b) có nucleotide A nằm ở vị trí đầu tiên?

Lời giải:

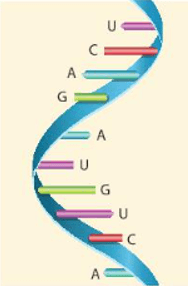
a) Có thể coi việc tạo nên một đoạn phân tử RNA có 4 phân tử nucleotide trong đó không có nucleotide A nào là một công việc gồm 4 công đoạn, mỗi đoạn ứng với việc chọn một trong ba loại nucleotide (C, G, U) cho mỗi vị trí (thứ nhất, thứ hai, thứ ba, thứ tư) của đoạn. Theo quy tắc nhân, 4 công đoạn có số cách thực hiện là:

3.3.3.3 = 34.

Vậy có nhiều nhất 34 đoạn phân tử RNA khác nhau cùng có 4 phân tử nucleotide nhưng không chứa nucleotide A.

b) Đang biên soạn

Lời giải bài tập Toán 10 Bài 1: Quy tắc cộng và quy tắc nhân hay, chi tiết khác:

Vận dụng trang 24 Toán 10 Tập 2 Chân trời sáng tạo

Giải Toán 10 Chân trời sáng tạo Bài 1: Quy tắc cộng và quy tắc nhân

Vận dụng trang 24 Toán lớp 10 Tập 2: Trong phần khởi động đầu bài học này, nếu công ty có 2 500 nhân viên thì số mã như vậy có đủ để cấp cho mỗi nhân viên một mã số riêng hay không?

Lời giải:

Bảng chữ cái tiếng Anh có tất cả 26 chữ cái;

Có tất cả 10 chữ số: 0; 1; 2; 3; 4; 5; 6; 7; 8; 9.

Công việc chọn mã số thẻ cho nhận viên như trên có thể coi gồm hai công đoạn:

- Công đoạn thứ nhất: Chọn một chữ cái từ 26 chữ cái có 26 cách;

- Công đoạn thứ hai: Ứng với mỗi cách chọn một chữ cái, có 10 cách chọn một chữ số ở giữa.

- Công đoạn thứ ba: Ứng với mỗi cách chọn một chữ cái và một chữ số đằng trước, có 10 cách chọn cho chữ số cuối cùng.

Theo quy tắc nhân, có: 26.10.10 = 2 600 cách tạo mã số thẻ cho nhân viên.

Vì số lượng nhân viên của công ty đó là 2 500 < 2 600 nên hoàn toàn có thể cấp đủ mã thẻ cho từng nhân viên.

Lời giải bài tập Toán 10 Bài 1: Quy tắc cộng và quy tắc nhân hay, chi tiết khác:

Bài 1 trang 24 Toán 10 Tập 2 Chân trời sáng tạo

Giải Toán 10 Chân trời sáng tạo Bài 1: Quy tắc cộng và quy tắc nhân

Bài 1 trang 24 Toán lớp 10 Tập 2: Một thùng chứa 6 quả dưa hấu, một thùng khác chứa 15 quả thanh long. Từ hai thùng này,

a) có bao nhiêu cách chọn một quả dưa hấu hoặc một quả thanh long?

b) có bao nhiêu cách chọn một quả dưa hấu và một quả thanh long?

Lời giải:

a) Số cách chọn một quả dưa hấu hoặc một quả thanh long được chia thành hai phương án:

Phương án 1: Chọn một quả thanh long, có 15 cách chọn.

Phương án 2: Chọn một quả dưa hấu, có 6 cách chọn.

Theo quy tắc cộng, ta có: 15 + 6 = 21 cách chọn một quả dưa hấu hoặc một quả thanh long.

Vậy có tất cả 21 cách chọn một quả dưa hấu hoặc một quả thanh long.

b) Số cách chọn một quả dưa hấu và một quả thanh long được chia thành hai công đoạn:

Công đoạn thứ 1: Chọn một quả dưa hấu, có 6 cách chọn.

Công đoạn thứ 2: Ứng với mỗi một quả dưa hấu đã chọn, có 15 cách chọn quả thanh long.

Theo quy tắc nhân, ta có: 15.6 = 90 cách một quả dưa hấu và một quả thanh long.

Vậy có tất cả 90 cách một quả dưa hấu và một quả thanh long.

Lời giải bài tập Toán 10 Bài 1: Quy tắc cộng và quy tắc nhân hay, chi tiết khác:

Bài 2 trang 24 Toán 10 Tập 2 Chân trời sáng tạo

Giải Toán 10 Chân trời sáng tạo Bài 1: Quy tắc cộng và quy tắc nhân

Bài 2 trang 24 Toán lớp 10 Tập 2: Tung đồng thời một đồng xu và một con xúc xắc, nhận được kết quả là mặt xuất hiện trên đồng xu (sấp hay ngửa) và số chấm xuất hiện trên con xúc xắc.

a) Tính số kết quả có thể xảy ra.

b) Vẽ sơ đồ hình cây và liệt kê tất cả các kết quả đó.

Lời giải:

a) Việc tung đồng thời một đồng xu và một con xúc xắc được chia thành hai công đoạn sau:

Công đoạn thứ nhất: Tung đồng xu, có 2 kết quả (sấp, ngửa).

Công đoạn thứ hai: Ứng với mỗi mặt của đồng xu, có 6 cách để tung xúc xắc (1 chấm, 2 chấm, 3 chấm, 4 chấm, 5 chấm, 6 chấm).

Theo quy tắc nhân, ta có: 2.6 = 12 kết quả khi tung đồng thời một đồng xu và một con xúc sắc.

b) Sơ đồ cây biểu thị các kết quả của việc tung đồng xu và xúc xắc:

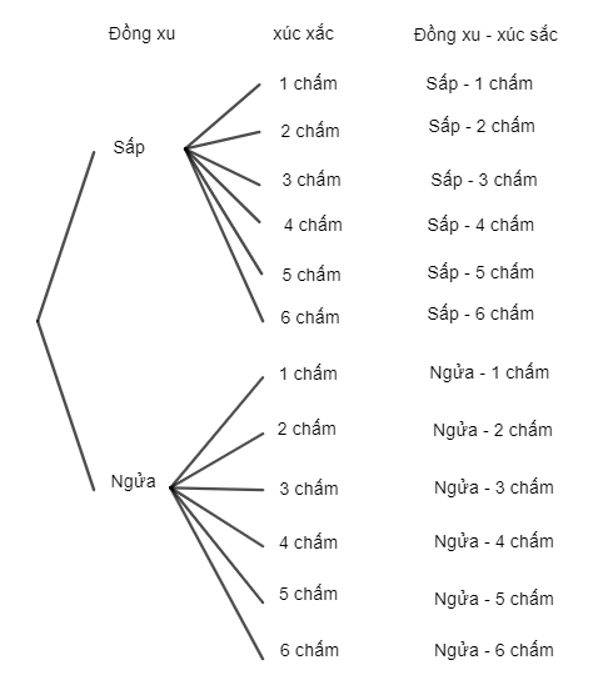
Lời giải bài tập Toán 10 Bài 1: Quy tắc cộng và quy tắc nhân hay, chi tiết khác:

Bài 3 trang 25 Toán 10 Tập 2 Chân trời sáng tạo

Giải Toán 10 Chân trời sáng tạo Bài 1: Quy tắc cộng và quy tắc nhân

Bài 3 trang 25 Toán lớp 10 Tập 2: Tại một nhà hàng chuyên phục vụ cơm trưa văn phòng, thực đơn có 5 món chính, 3 món phụ và 4 loại đồ uống. Tại đây thực khách có bao nhiêu cách chọn bữa trưa gồm món chính, món phụ và một loại đồ uống?

Lời giải:

Cách chọn bữa trưa được chia làm 3 công đoạn:

Công đoạn thứ nhất: Chọn món chính có 5 cách chọn.

Công đoạn thứ hai: Ứng với mỗi món chính có 3 cách chọn món phụ.

Công đoạn thứ ba: Ứng với mỗi món chính, một món phụ vừa chọn, có thêm 4 cách chọn đồ uống.

Theo quy tắc nhân có 5.3.4 = 60 cách để chọn bữa trưa.

Vậy có tất cả 60 cách để chọn một bữa trưa gồm món chính, món phụ và một loại đồ uống.

Lời giải bài tập Toán 10 Bài 1: Quy tắc cộng và quy tắc nhân hay, chi tiết khác:

Bài 4 trang 25 Toán 10 Tập 2 Chân trời sáng tạo

Giải Toán 10 Chân trời sáng tạo Bài 1: Quy tắc cộng và quy tắc nhân

Bài 4 trang 25 Toán lớp 10 Tập 2: Có bao nhiêu số tự nhiên lẻ có ba chữ số, trong đó chữ số hàng trăm là chữ số chẵn, chữ số hàng đơn vị là chữ số lẻ?

Lời giải:

Gọi số có ba chữ số cần tìm là $\overline{abc}$, với a, b, c là ba chữ số từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9.

Vì c là chữ số lẻ nên c có 5 cách chọn.

Ứng với mỗi cách chọn đó, có 4 cách chọn chữ số a khác 0 từ các chữ số chẵn.

Ứng với mỗi cách chọn đó, có 10 cách chọn chữ số b từ các chữ số trên.

Từ đó áp dụng quy tắc nhân, có 5.4.10 = 200 số tự nhiên có ba chữ số thỏa mãn yêu cầu đầu bài.

Vậy có 200 số tự nhiên lẻ có ba chữ số thỏa mãn chữ số hàng trăm là chữ số chẵn, chữ số hàng đơn vị là chữ số lẻ.

Lời giải bài tập Toán 10 Bài 1: Quy tắc cộng và quy tắc nhân hay, chi tiết khác:

Bài 5 trang 25 Toán 10 Tập 2 Chân trời sáng tạo

Giải Toán 10 Chân trời sáng tạo Bài 1: Quy tắc cộng và quy tắc nhân

Bài 5 trang 25 Toán lớp 10 Tập 2: An có thể đi từ nhà đến trường theo các con đường như Hình 11, trong đó có những con đường đi qua nhà sách.

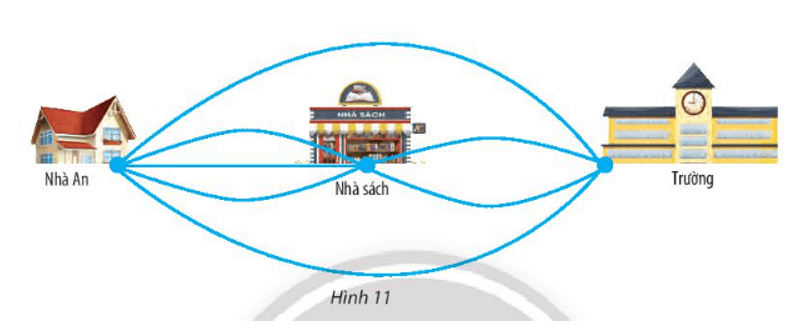
a) An có bao nhiêu cách đi từ nhà đến trường mà có đi qua nhà sách?

b) An có bao nhiêu cách đi từ nhà đến trường?

Lưu ý: Chỉ tính những đường đi qua các điểm (nhà An, nhà sách, trường) không quá một lần.

Lời giải:

a) Nếu An đi từ nhà đến trường mà đi qua nhà sách thì quãng đường chia làm hai giai đoạn:

Giai đoạn thứ nhất: Đi từ nhà đến nhà sách, có 3 cách.

Giai đoạn thứ hai: Đi từ nhà sách đến trường, có 2 cách.

Theo quy tắc nhân ta có 3.2 = 6 cách đi từ nhà đến trường mà qua nhà sách.

b) An có bao nhiêu cách đi từ nhà đến trường có hai phương án:

Phương án 1: Đi từ nhà An trực tiếp đến trường, có 2 cách.

Phương án 2: Đi từ nhà An đến trường qua nhà sách, có 6 cách.

Theo quy tắc cộng có 2 + 6 = 8 cách để đi từ nhà An đến trường.

Lời giải bài tập Toán 10 Bài 1: Quy tắc cộng và quy tắc nhân hay, chi tiết khác:

SBT Toán 10 Chân trời sáng tạo Bài 1: Quy tắc cộng và quy tắc nhân

Với giải sách bài tập Toán 10 Bài 1: Quy tắc cộng và quy tắc nhân sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 10 dễ dàng làm bài tập trong SBT Toán 10 Bài 1.

Giải SBT Toán 10 Chân trời sáng tạo Bài 1: Quy tắc cộng và quy tắc nhân

Quy tắc cộng và quy tắc nhân (Lý thuyết Toán lớp 10) - Chân trời sáng tạo

Với tóm tắt lý thuyết Toán 10 Bài 1: Quy tắc cộng và quy tắc nhân sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.

Quy tắc cộng và quy tắc nhân (Lý thuyết Toán lớp 10) - Chân trời sáng tạo

Lý thuyết Quy tắc cộng và quy tắc nhân

1. Quy tắc cộng

– Giả sử một công việc có thể được thực hiện theo phương án A hoặc B. Phương án A có m cách thực hiện, phương án B có n cách thực hiện không trùng với bất kì cách nào của phương án A. Khi đó, công việc có thể thực hiện theo m + n cách.

Ví dụ: Lớp 10A có 20 học sinh, lớp 10C có 24 học sinh. Có bao nhiêu cách cử 1 học sinh lớp 10A hoặc lớp 10C đi tham dự đại hội Đoàn trường?

Hướng dẫn giải

Công việc cử 1 học sinh đi có 2 phương án thực hiện:

Phương án 1: Cử 1 học sinh của lớp 10A, ta có 20 cách.

Phương án 2: Cử 1 học sinh của lớp 10C, ta có 24 cách.

Ta thấy mỗi cách thực hiện của phương án B đều không trùng với cách của phương án A. Do đó theo quy tắc cộng, có 20 + 24 = 44 cách cử 1 học sinh lớp 10A hoặc lớp 10C đi tham dự đại hội Đoàn trường.

2. Quy tắc nhân

– Giả sử một công việc được chia thành hai công đoạn. Công đoạn thứ nhất có m cách thực hiện và ứng với mỗi cách đó có n cách thực hiện công đoạn thứ hai. Khi đó công việc có thể thực hiện theo m. n cách.

Ví dụ:Từ nhà An đến trường đi qua 3 điểm A, B, C. Từ nhà An đến điểm A có 3 cách đi, từ điểm A đến điểm B có 4 cách đi, từ điểm B đến điểm C có 2 cách đi. Từ điểm C đến trường học có 2 cách đi. Hỏi có bao nhiêu cách từ nhà An đến trường?

Hướng dẫn giải

Từ nhà An đến trường đi qua 3 điểm A, B, C, như vậy có 4 công đoạn:

+ Công đoạn 1: Từ nhà An đến điểm A có 3 cách đi.

+ Công đoạn 2: Từ điểm A đến điểm B có 4 cách đi

+ Công đoạn 3: Từ điểm B đến điểm C có 2 cách đi.

+ Công đoạn 4: Từ điểm C đến trường học có 2 cách đi.

Do đó, theo quy tắc nhân, có 3. 4. 2. 2 = 48 cách đi từ nhà An đến trường.

Bài tập Quy tắc cộng và quy tắc nhân

Bài 1. Một giỏ hoa quả chứa 5 quả cam và 4 quả táo.

a) Hỏi có bao nhiêu cách chọn 1 quả cam hoặc 1 quả táo?

b) Hỏi có bao nhiêu cách chọn 1 quả cam và 1 quả táo?

Hướng dẫn giải

a) Chọn 1 quả cam hoặc 1 quả táo, có 2 phương án chọn:

+ Phương án 1: Chọn 1 quả cam trong 5 quả cam có 5 cách.

+ Phương án 2: Chọn 1 quả táo trong 4 quả táo có 4 cách.

Mỗi cách của phương án 2 đều không trùng với cách của phương án 1.

Do đó có 5 + 4 = 9 cách để chọn 1 quả cam hoặc 1 quả táo.

b) Chọn 1 quả cam và 1 quả táo có 2 công đoạn:

+ Công đoạn 1: chọn 1 quả cam có 5 cách.

+ Công đoạn 2: chọn 1 quả táo có 4 cách.

Theo quy tắc nhân, có 5. 4 = 20 cách chọn 1 quả cam và 1 quả táo.

Bài 2. Trong tủ sách của lớp Vân có 10 quyển sách Toán, 5 quyển sách Ngữ Văn và 8 quyển sách Tiếng Anh. Bạn Vân muốn chọn 1 quyển sách Toán, 1 quyển Ngữ Văn và 1 quyển Tiếng Anh để đọc. Hỏi Vân có bao nhiêu cách chọn?

Hướng dẫn giải

Chọn 1 quyển sách Toán, 1 quyển sách Tiếng Việt, 1 sách Tiếng Anh có 3 công đoạn:

+ Công đoạn 1: Chọn 1 quyển Toán có 10 cách.

+ Công đoạn 2: Chọn 1 quyển Ngữ Văn có 5 cách.

+ Công đoạn 3: Chọn 1 quyển Tiếng Anh có 8 cách.

Theo quy tắc nhân, Vân sẽ có 10. 5. 8 = 400 cách chọn 1 quyển sách Toán, 1 quyển sách Ngữ Văn và 1 quyển sách Tiếng Anh.

Bài 3.Có bao nhiêu số tự nhiên có 3 chữ số trong đó:

a) 3 chữ số đều là chữ số chẵn.

b) 2 chữ số hàng chục và hàng trăm là chữ số lẻ, chữ số hàng đơn vị là chữ số chẵn.

Hướng dẫn giải

Gọi số cần tìm có 3 chữ số là $\overline{abc}$ (với 0 < a < 9; 0 ≤ b, c ≤ 9; a, b, c ∈ ℕ).

Ta có a ∈{1; 2; …; 9}; b ∈{0; 1; 2; …; 9} và c ∈{0; 1; 2; …; 9}.

a) Lập số tự nhiên có 3 chữ số đều là chữ số chẵn có 3 công đoạn:

+ Công đoạn 1: Chọn chữ số hàng trăm: có 4 cách chọn (chọn một trong các chữ số 2; 4; 6; 8).

+ Công đoạn 2: Chọn chữ số hàng chục: có 5 cách chọn (chọn một trong các chữ số 0; 2; 4; 6; 8).

+ Công đoạn 3: Chọn chữ số hàng đơn vị: có 5 cách chọn (chọn một trong các chữ số 0; 2; 4; 6; 8).

Theo quy tắc nhân, có 4. 5. 5 = 100 cách chọn.

Vậy có 100 số tự nhiên có 3 chữ số đều là chữ số chẵn.

b) Lập số tự nhiên theo yêu cầu có 3 công đoạn:

+ Công đoạn 1: Chọn chữ số hàng trăm: có 5 cách chọn (chọn một trong các chữ số 1; 3; 5; 7; 9).

+ Công đoạn 2: Chọn chữ số hàng chục: có 5 cách chọn (chọn một trong các chữ số 1; 3; 5; 7; 9).

+ Công đoạn 3: Chọn chữ số hàng đơn vị: có 5 cách chọn (chọn một trong các chữ số 0; 2; 4; 6; 8).

Theo quy tắc nhân, có 5. 5. 5 = 125 cách chọn.

Vậy có 125 số tự nhiên có 3 chữ số mà 2 chữ số hàng chục và hàng trăm là chữ số lẻ, chữ số hàng đơn vị là chữ số chẵn.

Bài 4. Minh có thể đi từ nhà đến nhà sách theo các con đường như hình vẽ bên dưới, trong đó có những con đường đi qua Circle K và Highlands Coffee.

Hỏi Minh có bao nhiêu cách đi từ nhà đến nhà sách?

Hướng dẫn giải

– Đi từ nhà Minh đến nhà sách phải đi qua Circle K và Highlands Coffee có 3 công đoạn:

+ Công đoạn 1: Đi từ nhà Minh đến Circle K: có 3 cách.

+ Công đoạn 2: Đi từ Circle K đến Highlands Coffee: có 4 cách.

+ Công đoạn 3: Đi từ Highlands Coffee đến nhà sách: có 2 cách.

Do đó theo quy tắc nhân có 3. 4. 2 = 24 cách đi từ nhà Minh đến nhà sách.

Vậy có 24 cách đi từ nhà Minh đến nhà sách.

Học tốt Quy tắc cộng và quy tắc nhân

Các bài học để học tốt Quy tắc cộng và quy tắc nhân Toán lớp 10 hay khác:

15 Bài tập Quy tắc cộng và quy tắc nhân (có đáp án) - Chân trời sáng tạo Trắc nghiệm Toán 10

Với 15 bài tập trắc nghiệm Quy tắc cộng và quy tắc nhân Toán lớp 10 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Chân trời sáng tạo sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.

15 Bài tập Quy tắc cộng và quy tắc nhân (có đáp án) - Chân trời sáng tạo Trắc nghiệm Toán 10

Câu 1.An muốn qua nhà Bình để cùng Bình đến chơi nhà Cường. Từ nhà An đến nhà Bình có 4 con đường đi, từ nhà Bình đến nhà Cường có 6 con đường đi. Hỏi An có bao nhiêu cách chọn đường đi đến nhà Cường?

A.16;

B.10;

C.24;

D.36.

Câu 2. Có 10 cái bút khác nhau và 8 quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn 1 cái bút và 1 quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn?

A. 80;

B. 60;

C. 90;

D. 70.

Câu 3.Từ thành phố A đến thành phố B có 3 con đường, từ thành phố A đến thành phố C có 2 con đường, từ thành phố B đến thành phố D có 2 con đường, từ thành phố C đến thành phố D có 3 con đường, không có con đường nào nối từ thành phố C đến thành phố B. Hỏi có bao nhiêu con đường đi từ thành phố A đến thành phố D.

A. 6;

B. 12;

C. 18;

D. 36.

Câu 4. Cho các chữ số 2, 3, 4, 5, 6, 7, 8, 9 số các số tự nhiên chẵn có 3 chữ số lập thành từ các chữ số đã cho là

A. 36;

B. 18;

C. 256;

D. 108;

Câu 5. Từ các chữ số 0; 1; 2; 3; 4; 5; 6 có thể lập được bao nhiêu số tự nhiên chẵn có ba chữ số khác nhau?

A. 210;

B. 105;

C. 168;

D. 145.

Câu 6. Bạn Dũng có 9 quyển truyện tranh khác nhau và 6 quyển tiểu thuyết khác nhau. Bạn Dũng có bao nhiêu cách chọn ra một quyển sách để đọc vào cuối tuần.

A. 9;

B. 6;

C. 54;

D. 15.

Câu 7. Cho các số 1; 2; 3; 4; 5; 6; 7. Có bao nhiêu số tự nhiên gồm 5 chữ số khác nhau lấy từ 7 chữ số trên sao cho chữ số đầu tiên là số 3

A. 7⁵;

B. 360;

C. 240;

D. 2401.

Câu 8. Có bao nhiêu số chẵn gồm bốn chữ số được lập từ các số 0; 1; 2; 4; 5; 6; 8.

A. 2058;

B. 1470;

C. 520;

D. 368.

Câu 9.Có bao nhiêu số tự nhiên gồm 5chữ số chia hết cho 5

A. 13260;.

B. 20000;

C. 18000;

D. 12070.

Câu 10. Có bao nhiêu cách sắp xếp 3 nữ sinh và 3 nam sinh thành một hàng dọc sao cho các bạn nam đứng cạnh nhau và nữ đứng cạnh nhau:

A. 6;

B. 72;

C. 720;

D. 144.

Câu 11. Một liên đoàn bóng đá có 10 đội, mỗi đội phải đá 4 trận với mỗi đội khác, 2 trận ở sân nhà và 2 trận ở sân khách. Số trận đấu được sắp xếp là

A. 180;

B. 160;

C. 90;

D. 45.

Câu 12. Có bao nhiêu số tự nhiên có chín chữ số mà các chữ số của nó viết theo thứ tự giảm dần

A. 5;

B. 15;

C. 55;

D. 10.

Câu 13. Từ các chữ số 0; 2; 5; 3; 6; 8 có thể lập được bao nhiêu số tự nhiên gồm 6 chữ số đôi một khác nhau trong đó hai chữ số 0 và 5 không đứng cạnh nhau.

A. 384;

B. 120;

C. 216;

D. 600.

Câu 14.Từ các chữ số 0; 1; 2; 3; 4; 5; 8 lập được bao nhiêu số có ba chữ số đôi một khác nhau, chia hết cho 2 và 3.

A. 35;

B. 52;

C. 32;

D. 48.

Câu 15. Trên giá sách có 7 quyển sách Tiếng Nga khác nhau, 9 quyển sách Tiếng Anh khác nhau và 8 quyển sách Tiếng Việt khác nhau. Số cách chọn hai quyển sách khác loại là

A. 24;

B. 504;

C. 191;

D. 305.

Xem thêm bài tập trắc nghiệm Toán lớp 10 Chân trời sáng tạo có đáp án hay khác: