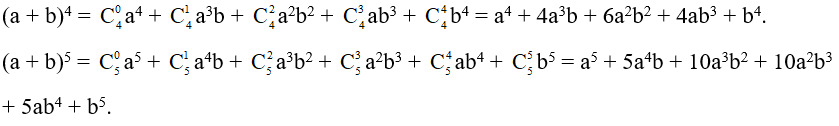Với giải bài tập Toán 10 Bài 25: Nhị thức Newton sách Kết nối tri thức hay nhất, chi tiết giúp học sinh lớp 10 dễ dàng làm bài tập Toán 10 Bài 25.

Giải Toán 10 Kết nối tri thức Bài 25: Nhị thức Newton

Giải Toán 10 trang 72

Mở đầu

Mở đầu trang 72 Toán 10 Tập 2 - Kết nối tri thức

Giải Toán 10 Kết nối tri thức Bài 25: Nhị thức Newton

Mở đầu trang 72 Toán 10 Tập 2: Ở lớp 8, khi học về hằng đẳng thức, ta đã biết khai triển: 

(a + b)² = a² + 2ab + b²;

(a + b)³ = a³ + 3a²b + 3ab² + b³. 

Quan sát các đơn thức ở vế phải của các đẳng thức trên, hãy nhận xét về quy luật số mũ của a và b. Có thể tìm được cách tính các hệ số của đơn thức trong khai triển (a + b)ⁿ khi n ∈ {4; 5} không?

Lời giải:

+) Ta có: a² + 2ab + b² = a² . b⁰ + 2 . a¹ . b¹ + b² . a⁰ 

a³ + 3a²b + 3ab² + b³ = a³ . b⁰ + 3 . a² .b¹ + 3 . a¹ . b² + a⁰ . b³

Quan sát vế phải của các đẳng thức, ta thấy số mũ của a giảm dần từ số mũ của biểu thức vế trái đến 0, còn số mũ của b tăng dần từ 0 đến số mũ của biểu thức ở vế trái. 

+) Sau khi học bài Nhị thức Newton này, ta có thể tìm được cách tính các hệ số của đơn thức trong khai triển (a + b)ⁿ khi n ∈ {4; 5}. 

Lời giải bài tập Toán 10 Bài 25: Nhị thức Newton hay, chi tiết khác:

HĐ1 trang 72 Toán 10 Tập 2 - Kết nối tri thức

Giải Toán 10 Kết nối tri thức Bài 25: Nhị thức Newton

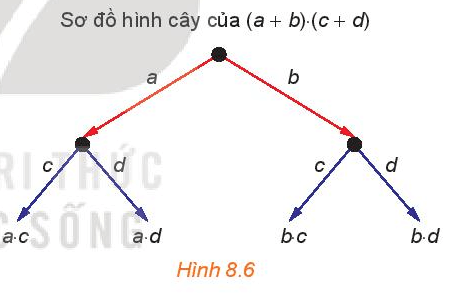
HĐ1 trang 72 Toán 10 Tập 2: Sơ đồ hình cây của tích hai nhị thức (a + b) . (c + d) được xây dựng như sau:

• Từ một điểm gốc, kẻ các mũi tên, mỗi mũi tên tương ứng với một đơn thức (gọi là nhãn của mũi tên) của nhị thức thứ nhất (H.8.6);

• Từ ngọn của mỗi mũi tên đã xây dựng, kẻ các mũi tên, mỗi mũi tên tương ứng với một đơn thức của nhị thức thứ hai;

• Tại ngọn của các mũi tên xây dựng tại bước sau cùng, ghi lại tích của các nhãn của các mũi tên đi từ điểm gốc đến đầu mút đó.

Hãy lấy tổng của các tích nhận được và so sánh kết quả với khai triển của tích (a + b) . (c + d). 

Lời giải:

Quan sát sơ đồ, ta thấy tổng các tích nhận được: a.c + a.d + b.c + b.d.

Khai triển của tích (a + b) . (c + d) = a . (c + d) + b . (c + d) = a.c + a.d + b.c + b.d.

Vậy tổng của các tích nhận được bằng với khai triển của tích (a + b) . (c + d). 

Lời giải bài tập Toán 10 Bài 25: Nhị thức Newton hay, chi tiết khác:

HĐ2 trang 72 Toán 10 Tập 2 - Kết nối tri thức

Giải Toán 10 Kết nối tri thức Bài 25: Nhị thức Newton

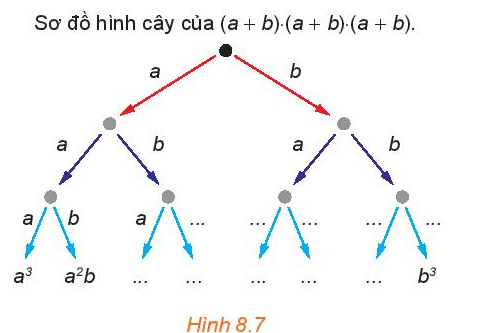
HĐ2 trang 72 Toán 10 Tập 2: Hãy cho biết các đơn thức còn thiếu (...) trong sơ đồ hình cây (H.8.7) của tích (a + b) . (a + b) . (a + b). 

Có bao nhiêu tích nhận được lần lượt bằng a³, a²b, ab², b³?

Hãy so sánh chúng với các hệ số nhận được khi khai triển (a + b)³.

Lời giải:

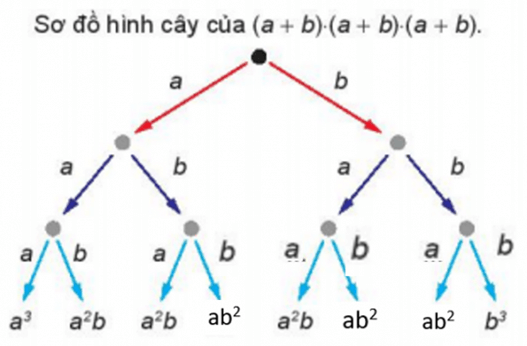
Theo quy tắc xây dựng sơ đồ hình cây như HĐ1, ta điền được các biểu thức trong sơ đồ hình cây của tích (a + b) . (a + b) . (a + b) như sau: 

Quan sát sơ đồ trên ta thấy, có 1 tích bằng a³, có 3 tích bằng a²b, có 3 tích bằng ab² và có 1 tích bằng b³.

Ở lớp 8, ta đã biết, khai triển (a + b)³ = a³ + 3a²b + 3ab² + b³.

Vậy hệ số của khai triển đúng bằng hệ số các tích nhận được.

Lời giải bài tập Toán 10 Bài 25: Nhị thức Newton hay, chi tiết khác:

HĐ3 trang 73 Toán 10 Tập 2 - Kết nối tri thức

Giải Toán 10 Kết nối tri thức Bài 25: Nhị thức Newton

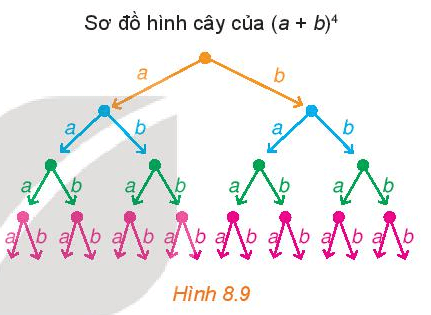
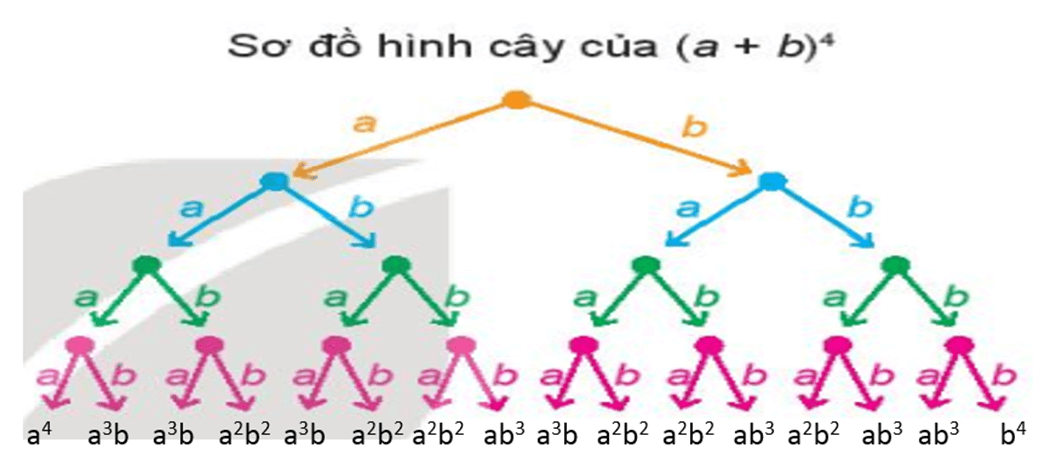
HĐ3 trang 73 Toán 10 Tập 2: Sơ đồ hình cây của khai triển (a + b)⁴ được mô tả như Hình 8.9. Sau khi khai triển, ta thu được một tổng gồm 2⁴ (theo quy tắc nhân) đơn thức có dạng x . y . z . t, trong đó mỗi x, y, z, t là a hoặc b. Chẳng hạn, nếu x, y, t là a, còn z là b thì ta có đơn thức a . a . b . a, thu gọn là a³b. Để có đơn thức này, thì trong 4 nhân tử x, y, z, t có 1 nhân tử là b, 3 nhân tử còn lại là a. Khi đó số đơn thức đồng dạng với a³b trong tổng là $C_4^1$.

Lập luận tương tự trên, dùng kiến thức về tổ hợp, hãy cho biết trong tổng nêu trên, có bao nhiêu đơn thức đồng dạng với mỗi đơn thức thu gọn sau:

• a⁴;

• a³b;

• a²b²;

• ab³;

• b⁴. 

Lời giải:

+ Để có đơn thức a⁴ thì phải có 4 nhân tử a, khi đó số đơn thức đồng dạng với a⁴ trong tổng là: $C_4^0$= 1, hay có 1 đơn thức a⁴.

+ Để có đơn thức a³b thì phải có 3 nhân tử a, 1 nhân tử b, khi đó số đơn thức đồng dạng với a³b trong tổng là: $C_4^1$= 4.

+ Để có đơn thức a²b² thì phải có 2 nhân tử a, 2 nhân tử b, khi đó số đơn thức đồng dạng với a²b² trong tổng là: $C_4^2$= 6.

+ Để có đơn thức ab³ thì phải có 1 nhân tử a, 3 nhân tử b, khi đó số đơn thức đồng dạng với ab³ trong tổng là: $C_4^3$= 4.

+ Để có đơn thức b⁴ thì phải có 4 nhân tử b, khi đó số đơn thức đồng dạng với b⁴ trong tổng là: $C_4^4$= 1, hay có 1 đơn thức b⁴.

Lời giải bài tập Toán 10 Bài 25: Nhị thức Newton hay, chi tiết khác:

Luyện tập 1 trang 73 Toán 10 Tập 2 - Kết nối tri thức

Giải Toán 10 Kết nối tri thức Bài 25: Nhị thức Newton

Luyện tập 1 trang 73 Toán 10 Tập 2: Khai triển (x – 2)⁴.

Lời giải:

Thay a = x và b = – 2 trong công thức khai triển của (a + b)⁴, ta được:

(x – 2)⁴ = x⁴ + 4x³ .(– 2) + 6x² . (–2)² + 4x . (– 2)³ + (– 2)⁴

  = x⁴ – 8x³ + 24x² – 32x + 16.

Lời giải bài tập Toán 10 Bài 25: Nhị thức Newton hay, chi tiết khác:

HĐ4 trang 74 Toán 10 Tập 2 - Kết nối tri thức

Giải Toán 10 Kết nối tri thức Bài 25: Nhị thức Newton

HĐ4 trang 74 Toán 10 Tập 2: Tương tự như HĐ3, sau khi khai triển (a + b)⁵, ta thu được một tổng gồm 2⁵ đơn thức có dạng x . y . z . t . u, trong đó mỗi kí hiệu x, y, z, t, u là a hoặc b. Chẳng hạn, nếu x, z là a, còn y, t, u là b thì ta có đơn thức a . b . a . b . b, thu gọn là a²b³. Để có đơn thức này, thì trong 5 nhân tử x, y, z, t, u có 3 nhân tử là b, 2 nhân tử còn lại là a. Khi đó số đơn thức đồng dạng với a²b³ trong tổng là $C_5^3$.

Lập luận tương tự như trên, dùng kiến thức về tổ hợp, hãy cho biết, trong tổng nhận được nêu trên có bao nhiêu đơn thức đồng dạng với mỗi đơn thức thu gọn sau:

• a⁵;

• a⁴b;

• a³b²;

• a²b³;

• ab⁴;

• b⁵.

Lời giải:

+ Để có đơn thức a⁵ thì phải có 5 nhân tử a, khi đó số đơn thức đồng dạng với a⁵ trong tổng là: $C_5^0$= 1, hay có 1 đơn thức a⁵.

+ Để có đơn thức a⁴b thì phải có 4 nhân tử a, 1 nhân tử b, khi đó số đơn thức đồng dạng với a⁴b trong tổng là: $C_5^1$= 5.

+ Để có đơn thức a³b² thì phải có 3 nhân tử a, 2 nhân tử b, khi đó số đơn thức đồng dạng với a³b² trong tổng là: $C_5^2$= 10.

+ Để có đơn thức a²b³ thì phải có 2 nhân tử a, 3 nhân tử b, khi đó số đơn thức đồng dạng với a²b³ trong tổng là: $C_5^3$= 10.

+ Để có đơn thức ab⁴ thì phải có 1 nhân tử a, 4 nhân tử b, khi đó số đơn thức đồng dạng với ab⁴ là: $C_5^4$= 5.

+ Để có đơn thức b⁵ thì phải có 5 nhân tử b, khi đó số đơn thức đồng dạng với b⁵ trong tổng là: $C_5^5$= 1.

Lời giải bài tập Toán 10 Bài 25: Nhị thức Newton hay, chi tiết khác:

Luyện tập 2 trang 74 Toán 10 Tập 2 - Kết nối tri thức

Giải Toán 10 Kết nối tri thức Bài 25: Nhị thức Newton

Luyện tập 2 trang 74 Toán 10 Tập 2: Khai triển (3x – 2)⁵.

Lời giải:

Thay a = 3x và b = – 2 trong công thức khai triển của (a + b)⁵, ta được:

(3x – 2)⁵

= (3x)⁵ + 5. (3x)⁴. (–2) + 10 . (3x)³ . (– 2)² + 10 . (3x)² . (– 2)³ + 5 . (3x) . (– 2)⁴ + (– 2)⁵

= 243x⁵ – 810x⁴ + 1080x³ – 720x² + 240x – 32.

Lời giải bài tập Toán 10 Bài 25: Nhị thức Newton hay, chi tiết khác:

Vận dụng trang 74 Toán 10 Tập 2 - Kết nối tri thức

Giải Toán 10 Kết nối tri thức Bài 25: Nhị thức Newton

Vận dụng trang 74 Toán 10 Tập 2:

a) Dùng hai số hạng đầu tiên trong khai triển của (1 + 0,05)⁴ để tính giá trị gần đúng của 1,05⁴.

b) Dùng máy tính cầm tay tính giá trị của 1,05⁴ và tính sai số tuyệt đối của giá trị gần đúng nhận được ở câu a.

Lời giải:

a) Khai triển: (1 + 0,05)⁴ = 1⁴ + 4 . 1³ . 0,05 + 6 . 1² . 0,05² + 4 . 1 . 0,05³ + 0,05⁴.

1,05⁴ ≈ 1⁴ + 4 . 1³ . 0,05 = 1 + 0,2 = 1,2. 

Vậy giá trị gần đúng của khai triển 1,05⁴là 1,2. 

b) Sử dụng máy tính cầm tay, ta tính được: 1,05⁴ ≈ 1,21550625

Ta có: ∆ ≈ |1,21550625 – 1,2| = 0,01550625 < 0,02

Sai số tuyệt đối là 0,02.

Lời giải bài tập Toán 10 Bài 25: Nhị thức Newton hay, chi tiết khác:

Bài 8.12 trang 74 Toán 10 Tập 2 - Kết nối tri thức

Giải Toán 10 Kết nối tri thức Bài 25: Nhị thức Newton

Bài 8.12 trang 74 Toán 10 Tập 2: Khai triển các đa thức:

a) (x – 3)⁴; 

b) (3x – 2y)⁴;

c) (x + 5)⁴ + (x – 5)⁴;

d) (x – 2y)⁵.

Lời giải:

Áp dụng các công thức khai triển của (a + b)⁴ và (a + b)⁵, ta như sau: 

a) (x – 3)⁴ = x⁴ + 4 . x³ . (–3) + 6 . x² . (–3)² + 4 . x . (–3)³ + (–3)⁴

= x⁴ –12x³ + 54x² – 108x + 81.

b) (3x – 2y)⁴ = (3x)⁴ + 4 . (3x)³ . (– 2y) + 6 . (3x)² . (– 2y)² + 4 . (3x) . (– 2y)³ + (– 2y)⁴

= 81x⁴ – 216x³y + 216x²y² – 96xy³ + 16y⁴.

c) (x + 5)⁴ + (x – 5)⁴  

= (x⁴ + 4x³. 5 + 6x² . 5² + 4x . 5³ + 5⁴) + [x⁴ + 4x³ . (– 5) + 6x² . (– 5)² + 4x . (– 5)³ + (– 5)⁴]

= (x⁴ + x⁴) + (20x³ – 20x³) + (150x² + 150x²) + (500x – 500x) + (625 + 625)

= 2x⁴ + 300x² + 1250.

d) (x – 2y)⁵ = x⁵ + 5x⁴ . (– 2y) + 10x³ . (– 2y)² + 10x² . (– 2y)³ + 5x . (2y)⁴ + (– 2y)⁵

= x⁵ – 10x⁴y + 40x³y² – 80x²y³ + 80xy⁴ – 32y⁵. 

Lời giải bài tập Toán 10 Bài 25: Nhị thức Newton hay, chi tiết khác:

Bài 8.13 trang 74 Toán 10 Tập 2 - Kết nối tri thức

Giải Toán 10 Kết nối tri thức Bài 25: Nhị thức Newton

Bài 8.13 trang 74 Toán 10 Tập 2: Tìm hệ số của x⁴ trong khai triển của (3x –1)⁵.

Lời giải:

Số hạng chứa x⁴ là: 5 . (3x)⁴ . (– 1) = – 405x⁴.

Vậy hệ số của x⁴ trong khai triển của (3x – 1)⁵ là: – 405.

Lời giải bài tập Toán 10 Bài 25: Nhị thức Newton hay, chi tiết khác:

Bài 8.14 trang 74 Toán 10 Tập 2 - Kết nối tri thức

Giải Toán 10 Kết nối tri thức Bài 25: Nhị thức Newton

Bài 8.14 trang 74 Toán 10 Tập 2: Biểu diễn ${\left(3+\sqrt{2}\right)}^5-{\left(3-\sqrt{2}\right)}^5$ dưới dạng $a+b\sqrt{2}$ với a, b là các số nguyên.

Lời giải:

Ta có: ${\left(3+\sqrt{2}\right)}^5=3^5+{5.3}^4.\sqrt{2}+{10.3}^3.{\left(\sqrt{2}\right)}^2+{10.3}^2.{\left(\sqrt{2}\right)}^3+\mathrm{5.3.}{\left(\sqrt{2}\right)}^4+{\left(\sqrt{2}\right)}^5$

$=3^5+{5.3}^4.\sqrt{2}+{10.3}^3.2+{10.3}^2\mathrm{.2.}\sqrt{2}+\mathrm{5.3.4}+4\sqrt{2}$

${\left(3-\sqrt{2}\right)}^5=3^5+{5.3}^4.\left(-\sqrt{2}\right)+{10.3}^3.{\left(-\sqrt{2}\right)}^2+{10.3}^2.{\left(-\sqrt{2}\right)}^3+\mathrm{5.3.}{\left(-\sqrt{2}\right)}^4+{\left(-\sqrt{2}\right)}^5$

$=3^5-{5.3}^4.\sqrt{2}+{10.3}^3.2-{10.3}^2\mathrm{.2.}\sqrt{2}+\mathrm{5.3.4}-4\sqrt{2}$

Suy ra: ${\left(3+\sqrt{2}\right)}^5-{\left(3-\sqrt{2}\right)}^5=2\left({5.3}^4.\sqrt{2}+{10.3}^2.2\sqrt{2}+4\sqrt{2}\right)$

$=2.589\sqrt{2}=1178\sqrt{2}=0+1178\sqrt{2}$. 

Vậy biểu diễn ${\left(3+\sqrt{2}\right)}^5-{\left(3-\sqrt{2}\right)}^5$ dưới dạng $a+b\sqrt{2}$ với a, b là các số nguyên ta được $0+1178\sqrt{2}$. 

Lời giải bài tập Toán 10 Bài 25: Nhị thức Newton hay, chi tiết khác:

Bài 8.15 trang 75 Toán 10 Tập 2 - Kết nối tri thức

Giải Toán 10 Kết nối tri thức Bài 25: Nhị thức Newton

Bài 8.15 trang 75 Toán 10 Tập 2: a) Dùng hai số hạng đầu tiên trong khai triển của (1 + 0,02)⁵ để tính giá trị gần đúng của 1,02⁵.

b) Dùng máy tính cầm tay tính giá trị của 1,02⁵ và tính sai số tuyệt đối của giá trị gần đúng nhận được ở câu a.

Lời giải:

a) Ta có khai triển: 

(1 + 0,02)⁵ = 1⁵ + 5 . 1⁴ . (0,02) + 10 . 1³ . (0,02)² + 10 . 1² . (0,02)³ + 5 . 1 . (0,02)⁴ + (0,02)⁵

 Do đó: 1,02⁵ = (1 + 0,02)⁵  ≈ 1⁵ + 5 . 1⁴ . 0,02 = 1,1. 

b) Sử dụng máy tính cầm tay ta tính được: 1,02⁵ ≈ 1,104080803

Ta có: ∆ ≈ |1,104080803 – 1,1| = 0,004080803 < 0,005

Sai số tuyệt đối là 0,005.

Lời giải bài tập Toán 10 Bài 25: Nhị thức Newton hay, chi tiết khác:

Bài 8.16 trang 75 Toán 10 Tập 2 - Kết nối tri thức

Giải Toán 10 Kết nối tri thức Bài 25: Nhị thức Newton

Bài 8.16 trang 75 Toán 10 Tập 2: Số dân của một tình ở thời điểm hiện tại là khoảng 800 nghìn người. Giả sử rằng tỉ lệ tăng dân số hằng năm của tỉnh đó là r%.

a) Viết công thức tính số dân của tỉnh đó sau 1 năm, sau 2 năm. Từ đó suy ra công thức tính số dân của tỉnh đó sau 5 năm nữa là $P=800{\left(1+\frac{r}{100}\right)}^5$(nghìn người).

b) Với r = 1,5, dùng hai số hạng đầu trong khai triển của (1 + 0,015)⁵, hãy ước tính số dân của tỉnh đó sau 5 năm nữa (theo đơn vị nghìn người).

Lời giải:

a) Để tính số dân năm sau, ta lấy số dân năm trước cộng với số dân tăng hằng năm (Số dân tăng hằng năm là r% của số dân năm trước). 

Số dân của tỉnh đó sau 1 năm là: 

$P_1=800+800.r\%=800\left(1+r\%\right)=800{\left(1+\frac{r}{100}\right)}^1$(nghìn người).

Số dân của tỉnh đó sau 2 năm là:  

$P_2=P_1+P_1.r\%=800{\left(1+\frac{r}{100}\right)}^1+800{\left(1+\frac{r}{100}\right)}^1.\frac{r}{100}$

$=800{\left(1+\frac{r}{100}\right)}^1\left(1+\frac{r}{100}\right)=800{\left(1+\frac{r}{100}\right)}^2$(nghìn người).

Do đó, công thức tính số dân của tỉnh đó sau 5 năm nữa là: $P_5=800{\left(1+\frac{r}{100}\right)}^5$(nghìn người).

b) Với r = 1,5, suy ra $\frac{r}{100}=\frac{\mathrm{1,5}}{100}=\mathrm{0,015}$.

Ta có khai triển: 

(1 + 0,015)⁵ = 1⁵ + 5 . 1⁴ . 0,015 + 10 . 1³ . (0,015)² + 10 . 1². (0,015)³ + 5 . 1 . (0,015)⁴ + (0,015)⁵. 

Do đó: (1 + 0,015)⁵ ≈ 1⁵ + 5 . 1⁴ . 0,015 = 1,075. 

Số dân của tỉnh đó sau 5 năm nữa là: 

P₅ = 800 . (1 + 0,015)⁵≈ 800 . 1,075 = 860 (nghìn người)

Vậy số dân của tỉnh đó sau 5 năm nữa xấp xỉ khoảng 860 nghìn người. 

Lời giải bài tập Toán 10 Bài 25: Nhị thức Newton hay, chi tiết khác:

Sách bài tập Toán 10 Bài 25: Nhị thức Newton - Kết nối tri thức

Với giải sách bài tập Toán 10 Bài 25: Nhị thức Newton sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 Bài 25.

Sách bài tập Toán 10 Bài 25: Nhị thức Newton - Kết nối tri thức

Giải SBT Toán 10 trang 57 Tập 2

Nhị thức Newton (Lý thuyết Toán lớp 10) | Kết nối tri thức

Với tóm tắt lý thuyết Toán 10 Bài 25: Nhị thức Newton sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 10 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.

Nhị thức Newton (Lý thuyết Toán lớp 10) | Kết nối tri thức

Lý thuyết Nhị thức Newton

A. Lý thuyết

Nhận xét: Các tích nhận được từ sơ đồ hình cây của một tích các đa thức giống như cách lấy ra một đơn thức từ mỗi đa thức rồi nhân lại với nhau. Tổng của chúng cho ta khai triển của tích các đa thức đã cho.

Ví dụ: Sơ đồ hình cây của khai triển: (a + b)⁴

Ta có: (a + b)⁴ = (a + b).(a + b).(a + b).(a + b)

+ Từ một điểm gốc, kẻ các mũi tên, mỗi mũi tên tương ứng với một đơn thức của nhị thức thứ nhất là a và b.

+ Từ ngọn của mỗi mũi tên đã xây dựng, kẻ các mũi tên, mỗi mũi tên tương ứng với một đơn thức của nhị thức thứ hai là a và b.

+ Làm tương tự cho đến nhị thức thứ tư.

+ Tại ngọn của mũi tên xây dựng tại bước cuối cùng, ta ghi lại các tích của các nhãn của các mũi tên đi từ điểm gốc đến đầu mút đó.

Nhị thức Newton:

Ví dụ:

a) Khai triển (1 + x)⁴ ;

b) Khai triển (2x – 3)⁵.

Hướng dẫn giải

a) Ta có :

(1 + x)⁴ = $C_4^0$1⁴ + $C_4^1$1³.x + $C_4^2$1²x² + $C_4^3$1.x³ + $C_4^4$>x⁴

= 1⁴ + 4.1³x + 6.1².x² + 4.1.x³ + x⁴

= 1 + 4x + 6x² + 4x³ + x⁴.

Vậy (1 + x)⁴ = 1 + 4x + 6x² + 4x³ + x⁴.

b) Ta có :

(x + 3)⁵ = $C_5^0$x⁵ + $C_5^1$x⁴.3 + $C_5^2$x³.3² + $C_5^3$>x².3³ + $C_5^4$x.3⁴ + $C_5^5$3⁵

= x⁵ + 5x⁴.3 + 10x³.3² + 10x².3³ + 5x.3⁴ + 3⁵

= x⁵ + 15x⁴ + 90x³ + 270x² + 405x + 243.

Nhận xét: Các công thức khai triển (a + b)ⁿ với n ∈ {4 ; 5}, là một công cụ hiệu quả để tính chính xác hoặc xấp xỉ một số đại lượng mà không cần dùng máy tính.

Ví dụ: Dùng hai số hạng đầu của khai triển (1 + 0,02)⁵ để tính giá trị gần đúng của 1,02⁵.

Hướng dẫn giải

Ta có: (1 + 0,02)⁵ = 1⁵ + 5.1⁴. 0,02 + 10.1³.0,02² + 10.1².0,02³ + 5.1.0,02⁴ + 0,02⁵

= 1 + 0,1 + 10.1³.0,02² + 10.1².0,02³ + 5.1.0,02⁴ + 0,02⁵.

Vì 1 + 0,1 = 1,1 nên (1 + 0,02)⁵ ≈ 1,1, tức là 1,02⁵ ≈ 1,1.

Vậy 1,02⁵ ≈ 1,1.

Bài tập Nhị thức Newton

Bài 1: Khai triển các đa thức sau :

a) (2x – 1)⁴ ;

b) (x + 4)⁵ + (x – 4)⁵.

Hướng dẫn giải

a) Ta có: (2x – 1)⁴ = (2x)⁴ + 4(2x)³.(–1) + 6(2x)².(–1)² + 4.2x.(–1)³ + (–1)⁴.

= 16x⁴ – 32x³ + 24x² – 8x + 1.

Vậy : (2x – 1)⁴ = 16x⁴ – 32x³ + 24x² – 8x + 1.

b) Ta có:

(x + 4)⁵ + (x – 4)⁵ = [x⁵ + 5x⁴.4 + 10.x³.4² + 10.x².4³ + 5.x.4⁴ + 4⁵] + [x⁵ + 5x⁴.(–4) + 10.x³.(–4)² + 10.x².(–4)³ + 5.x.(–4)⁴ + (–4)⁵]

= [x⁵ + 20x⁴ + 160x³ + 640x² + 1280x + 1024] + [x⁵ – 20x⁴ + 160x³ – 640x² + 1280x –1024]

= x⁵ + 20x⁴ + 160x³ + 640x² + 1280x + 1024 + x⁵ – 20x⁴ + 160x³ – 640x² + 1280x –1024 = 2x⁵ + 320x³ + 2560x.

Vậy (x + 4)⁵ + (x – 4)⁵ = 2x⁵ + 320 x³ + 2560x.

Bài 2 :

a) Dùng hai số hạng đầu của khai triển (2 + 0,01)⁴ để tính giá trị gần đúng của 2,01⁴.

b) Dùng máy tính cầm tay để tính giá trị của 2,01⁴ và tính sai số tuyệt đối của giá trị gần đúng nhận được ở câu a.

Hướng dẫn giải

a) Ta có:(2 + 0,01)⁴ = 2⁴ + 4.2³.0,01 + 6.2².0,01² + 4.2.0,01³ + 0,01⁴

= 16 + 0,32 + 6.2².0,01² + 4.2.0,01³ + 0,01⁴

Vì 16 + 0,32 = 16,32 nên (2 + 0,01)⁴ ≈ 16,32, tức là 2,01⁴ ≈ 16,32.

Vậy 2,01⁴ ≈ 16,32.

b) Dùng máy tính cầm tay ta tính được giá trị của 2,01⁴ = 16,32240801....

Ta có: 16,32 < 2,01⁴ <16,33

Suy ra: |16,32 – 2,01⁴| < |16,33 – 16, 32| = 0,01.

Vậy với giá trị gần đúng 16,32 thì sai số tuyệt đối không vượt quá 0,01.

Học tốt Nhị thức Newton

Các bài học để học tốt Nhị thức Newton Toán lớp 10 hay khác:

15 Bài tập Nhi thức Newton (Trắc nghiệm Toán lớp 10 có đáp án) - Kết nối tri thức

Với 15 bài tập trắc nghiệm Nhi thức Newton Toán lớp 10 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.

15 Bài tập Nhi thức Newton (Trắc nghiệm Toán lớp 10 có đáp án) - Kết nối tri thức

Câu 1. Trong khai triển nhị thức (a + 2)^{n + 6} (n $\in$ ℕ). Có tất cả 17 số hạng. Vậy n bằng

A. 17;

B. 11;

C. 10;

D. 12.

Câu 2. Tổng số mũ của a và b trong mỗi hạng tử khi khai triển biểu thức (a + b)⁷ bằng

A. 5

B. 6

C. 7

D. 8

Câu 3. Biểu thức $C_9^7$5x)²(-6y²)⁷ là một số hạng trong khai triển nhị thức nào dưới đây

A. (5x – 6y)⁵

B. (5x – 6y²)⁷

C. (5x – 6y²)⁹

D. (5x – 6y²)¹⁸

Câu 4. Số hạng tử trong khai triển (2x + y)⁶ bằng

A. 7

B. 6 

C. 5

D. 4

Câu 5. Hệ số của x⁷ trong khai triển của (3 – x)⁹ là

A. 36;

B. 324;

C. - 324;

D. – 36.

Câu 6. Hệ số của x⁵ trong khai triển (1 + x)¹² bằng

A. 820;

B. 210;

C. 792;

D. 220.

Câu 7. Trong khai triển nhị thức (2a – 1)⁶ ba số hạng đầu là:

A. 2a⁶ – 6a⁵ + 15a⁴;

B. 2a⁶ – 12a⁵ + 30a⁴;

C. 64a⁶ – 192a⁵ + 480a⁴;

D. 64a⁶ – 192a⁵ + 240a⁴.

Câu 8. Khai triển nhị thức (2x + y)⁵ ta được kết quả là:

A. 32x⁵ + 16x⁴y + 8x³y² + 4x²y³ + 2xy⁴ + y⁵

B. 32x⁵ + 80x⁴y + 80x³y² + 40x²y³ + 10xy⁴ + y⁵

C. 2x⁵ + 10x⁴y + 20x³y² + 20x²y³ + 10xy⁴ + y⁵

D. 32x⁵ + 10000x⁴y + 80000x³y² + 400x²y³ + 10xy⁴ + y⁵

Câu 9. Trong khai triển (3x – y)⁷ số hạng chứa x⁴y³ là:

A. – 2835x⁴y³

B. 2835x⁴y³

C. 945x⁴y³

D. – 945x⁴y³

Câu 10. Trong khai triển ${\left(x+\frac{8}{x^2}\right)}^9$ số hạng không chứa x là:

A. 4308

B. 86016

C. 84

D. 43008

Câu 11. Trong khai triển (2x – 1)¹⁰ hệ số của số hạng chứa x⁸ là:

A. – 11520

B. 45

C. 256

D. 11520

Câu 12. Khai triển nhị thức (2x + 3)⁴ ta được kết quả là

A. x⁴ + 216x³ + 216x² + 96x + 81

B. 16x⁴ + 216x³ + 216x² + 96x + 81

C. 16x⁴ + 96x³ + 216x² + 216x + 81

D. x⁴ + 96x³ + 216x² + 216x + 81

Câu 13. Biết hệ số của x² trong khai triển của (1 – 3x)ⁿ là 90. Giá trị của n là

A. n = 5

B. n = 8

C. n = 6

D. n = 7

Câu 14. Tìm số hạng không chứa x trong khai triển ${\left(x^2-\frac{1}{x}\right)}^n$$A_n^2-C_n^2=105$

A. – 3003

B. – 5005

C. 5005

D. 3003

Câu 15. Với n là số nguyên dương thỏa mãn $C_n^1+C_n^2=55$ hệ số của x⁵ trong khai triển của biểu thức ${\left(x^3+\frac{2}{x^2}\right)}^n$bằng

A. 8064

B. 3360

C. 8440

D. 6840

Xem thêm bài tập trắc nghiệm Toán lớp 10 Kết nối tri thức có đáp án hay khác: