Với giải bài tập Toán 11 Bài 1: Hai đường thẳng vuông góc sách Cánh diều hay nhất, chi tiết giúp học sinh lớp 11 dễ dàng làm bài tập Toán 11 Bài 1.

Giải Toán 11 Cánh diều Bài 1: Hai đường thẳng vuông góc

Giải Toán 11 trang 77

Câu hỏi khởi động trang 77 Toán 11 Tập 2 Cánh diều

Giải Toán 11 Bài 1: Hai đường thẳng vuông góc - Cánh diều

Câu hỏi khởi động trang 77 Toán 11 Tập 2: Trong Hình 1, hai đường thẳng a, b gợi nên hình ảnh hai đường thẳng vuông góc trong không gian.

Trong không gian, thế nào là hai đường thẳng vuông góc với nhau?

Lời giải:

Dựa vào hình vẽ ta thấy hai đường thẳng a và b lần lượt nằm trong hai mặt phẳng tường bên và sàn nhà, mà mặt phẳng tường bên và sàn nhà vuông góc với nhau. Vậy nên trong không gian, hai đường thẳng vuông góc với nhau là hai đường thẳng nằm trong hai mặt phẳng vuông góc với nhau.

Lời giải bài tập Toán 11 Bài 1: Hai đường thẳng vuông góc hay, chi tiết khác:

Hoạt động 1 trang 77 Toán 11 Tập 2 Cánh diều

Giải Toán 11 Bài 1: Hai đường thẳng vuông góc - Cánh diều

Hoạt động 1 trang 77 Toán 11 Tập 2: Trong mặt phẳng cho hai đường thẳng a, b.

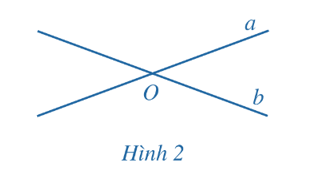
a) Nếu a và b cắt nhau tại điểm O (Hình 2) thì góc giữa hai đường thẳng a, b được xác định như thế nào?

b) Nếu a // b thì góc giữa a và b bằng bao nhiêu độ?

c) Nếu a và b trùng nhau thì góc giữa  a và b bằng bao nhiêu độ?

Lời giải:

a) Nếu a và b cắt nhau tại O thì góc giữa hai đường thẳng a, b là góc nhỏ nhất trong 4 góc được tạo thành hay góc giữa hai đường thẳng a, b lớn hơn 0° và không vượt quá 90°.

b) Nếu a // b thì góc giữa hai đường thẳng a và b bằng 0°.

c) Nếu a và b trùng nhau thì góc giữa a và b bằng 0°.

Lời giải bài tập Toán 11 Bài 1: Hai đường thẳng vuông góc hay, chi tiết khác:

Luyện tập 1 trang 78 Toán 11 Tập 2 Cánh diều

Giải Toán 11 Bài 1: Hai đường thẳng vuông góc - Cánh diều

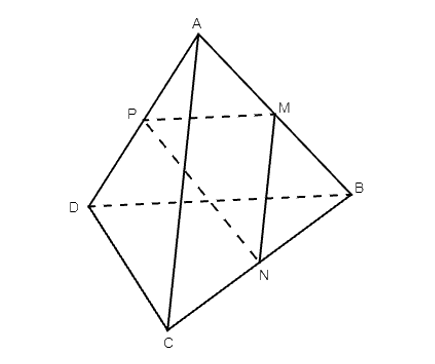
Luyện tập 1 trang 78 Toán 11 Tập 2: Cho tứ diện ABCD có M, N, P lần lượt là trung điểm của AB, BC, DA. Biết tam giác MNP đều. Tính góc giữa hai đường thẳng AC và BD.

Lời giải:

Xét tam giác ABC có: M, N lần lượt là trung điểm của AB và BC.

Suy ra MN là đường trung bình của tam giác ABC.

Nên MN // AC. (1)

Xét tam giác ABD có: M, P lần lượt là trung điểm của AB và AD.

Suy ra MP là đường trung bình của tam giác ABD.

Nên MP // BD. (2)

Từ (1) và (2) ta có: (AC, BD) = (MN, MP) = <$\widehat{NMP}$ = 60° (do tam giác MNP đều).

Vậy góc giữa hai đường thẳng AC và BD bằng 60°.

Lời giải bài tập Toán 11 Bài 1: Hai đường thẳng vuông góc hay, chi tiết khác:

Hoạt động 2 trang 78 Toán 11 Tập 2 Cánh diều

Giải Toán 11 Bài 1: Hai đường thẳng vuông góc - Cánh diều

Hoạt động 2 trang 78 Toán 11 Tập 2: Trong Hình 1 ở phần mở đầu, hai đường thẳng a, b gợi nên hình ảnh hai đường thẳng vuông góc. Góc giữa a và b bằng bao nhiêu độ?

Lời giải:

Do hai đường thẳng a và b vuông góc với nhau nên góc giữa a và b bằng 90°.

Lời giải bài tập Toán 11 Bài 1: Hai đường thẳng vuông góc hay, chi tiết khác:

Luyện tập 2 trang 79 Toán 11 Tập 2 Cánh diều

Giải Toán 11 Bài 1: Hai đường thẳng vuông góc - Cánh diều

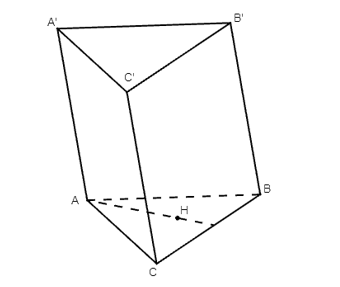
Luyện tập 2 trang 79 Toán 11 Tập 2: Cho hình lăng trụ ABC.A’B’C’ có H là trực tâm của tam giác ABC. Chứng minh rằng AH ⊥ B’C’.

Lời giải:

Do H là trực tâm tam giác ABC nên AH ⊥ BC. (1)

Do ABC.A’B’C’ là hình lăng trụ nên B’C’ // BC. (2)

Từ (1), (2) ta có AH ⊥ B’C’.

Lời giải bài tập Toán 11 Bài 1: Hai đường thẳng vuông góc hay, chi tiết khác:

Bài 1 trang 79 Toán 11 Tập 2 Cánh diều

Giải Toán 11 Bài 1: Hai đường thẳng vuông góc - Cánh diều

Bài 1 trang 79 Toán 11 Tập 2: Hình 6 gợi nên hình ảnh 5 cặp đường thẳng vuông góc. Hãy chỉ ra 5 cặp đường thẳng đó.

Lời giải:

Ta có 5 cặp đường thẳng vuông góc là: a và b; a và c; b và c; c và d; a và d.

⦁ 4 cặp đường thẳng vuông góc a và b; a và c; b và c; c và d ta có thể dễ dàng nhìn thấy được từ hình vẽ.

⦁ Cặp đường thẳng a và d vuông góc với nhau: vì a ⊥ b mà b // d suy ra a ⊥ d.

Lời giải bài tập Toán 11 Bài 1: Hai đường thẳng vuông góc hay, chi tiết khác:

Bài 2 trang 79 Toán 11 Tập 2 Cánh diều

Giải Toán 11 Bài 1: Hai đường thẳng vuông góc - Cánh diều

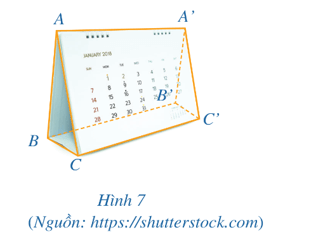
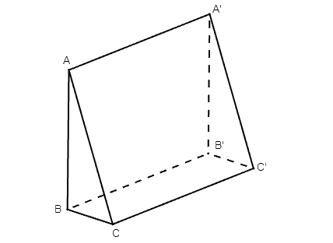
Bài 2 trang 79 Toán 11 Tập 2: Trong Hình 7 cho ABB’A’, BCC’B’, ACC’A’ là các hình chữ nhật. Chứng minh rằng AB ⊥ CC’, AA’ ⊥ BC.

Lời giải:

⦁ Do ABB’A’ là hình chữ nhật nên AB ⊥ BB’.

Do BCC’B’ là hình chữ nhật nên CC’ // BB’.

Từ đó ta có AB ⊥ CC’.

⦁  Do BCC’B’ là hình chữ nhật nên BC ⊥ CC’.

Do AA'C'C là hình chữ nhật nên AA’ // CC’.

Từ đó ta có BC ⊥ AA’ hay AA’ ⊥ BC.

Lời giải bài tập Toán 11 Bài 1: Hai đường thẳng vuông góc hay, chi tiết khác:

Bài 3 trang 79 Toán 11 Tập 2 Cánh diều

Giải Toán 11 Bài 1: Hai đường thẳng vuông góc - Cánh diều

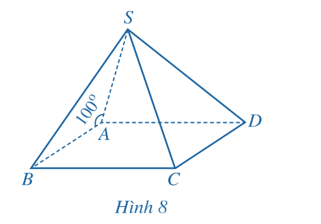
Bài 3 trang 79 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và $\widehat{SAB}=100°$ (Hình 8). Tính góc giữa hai đường thẳng:

a) SA và AB;

b) SA và CD.

Lời giải:

a) Vì $\widehat{SAB}=100°$ nên $\left(SA,AB\right)=180°-\widehat{SAB}=180°-100°=80°.$

Vậy góc giữa hai đường thẳng SA và AB bằng 80°.

b) Do ABCD là hình bình hành nên AB // CD.

Suy ra (SA, CD) = (SA, AB) = 80° (theo câu a).

Vậy góc giữa hai đường thẳng SA và CD bằng 80°.

Lời giải bài tập Toán 11 Bài 1: Hai đường thẳng vuông góc hay, chi tiết khác:

Bài 4 trang 79 Toán 11 Tập 2 Cánh diều

Giải Toán 11 Bài 1: Hai đường thẳng vuông góc - Cánh diều

Bài 4 trang 79 Toán 11 Tập 2: Bạn Hoa nói rằng: “Nếu hai đường thẳng phân biệt a và b cùng vuông góc với đường thẳng c thì a và b vuông góc với nhau”. Bạn Hoa nói đúng hay sai? Vì sao?

Lời giải:

Bạn Hoa nói sai. Vì nếu a, b, c cùng nằm trong một mặt phẳng.

Theo quan hệ từ vuông góc tới song song trong mặt phẳng ta có: a ⊥ b và b ⊥ c thì a // b.

Lời giải bài tập Toán 11 Bài 1: Hai đường thẳng vuông góc hay, chi tiết khác: