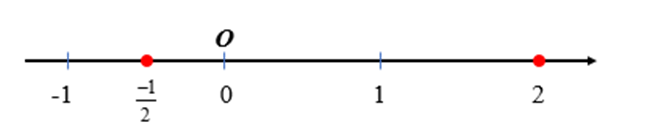Với giải bài tập Toán 7 Bài 2: Tập hợp R các số thực sách Cánh diều hay nhất, chi tiết giúp học sinh lớp 7 dễ dàng làm bài tập Toán 7 Bài 2:

Giải Toán 7 Cánh diều Bài 2: Tập hợp R các số thực

Video Giải Toán 7 Bài 2: Tập hợp R các số thực - Cô Ngô Vân (Giáo viên VietJack)

Hoạt động khởi động

Giải Toán 7 trang 38 Tập 1

Khởi động trang 38 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 2: Tập hợp ℝ các số thực - Cánh diều

Khởi động trang 38 Toán lớp 7 Tập 1: Các số hữu tỉ và vô tỉ được gọi chung là số gì?

Lời giải:

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

Các số hữu tỉ và vô tỉ được gọi chung là số thực. Tập hợp các số thực được kí hiệu là ℝ.

Lời giải bài tập Toán 7 Bài 2: Tập hợp R các số thực hay, chi tiết khác:

Hoạt động 1 trang 38 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 2: Tập hợp ℝ các số thực - Cánh diều

Hoạt động 1 trang 38 Toán lớp 7 Tập 1:

a) Nếu hai ví dụ về số hữu tỉ.

b) Nêu hai ví dụ về số vô tỉ.

Lời giải:

a) Hai ví dụ về số hữu tỉ là: $\frac{1}{3}; 0,5$

b) Hai ví dụ về số vô tỉ là: $\sqrt{2}; \sqrt{11}$

Lời giải bài tập Toán 7 Bài 2: Tập hợp R các số thực hay, chi tiết khác:

Hoạt động 2 trang 38 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 2: Tập hợp ℝ các số thực - Cánh diều

Hoạt động 2 trang 38 Toán lớp 7 Tập 1:

a) Nêu biểu diễn thập phân của số hữu tỉ.

b) Nêu biểu diễn thập phân của số vô tỉ.

Lời giải:

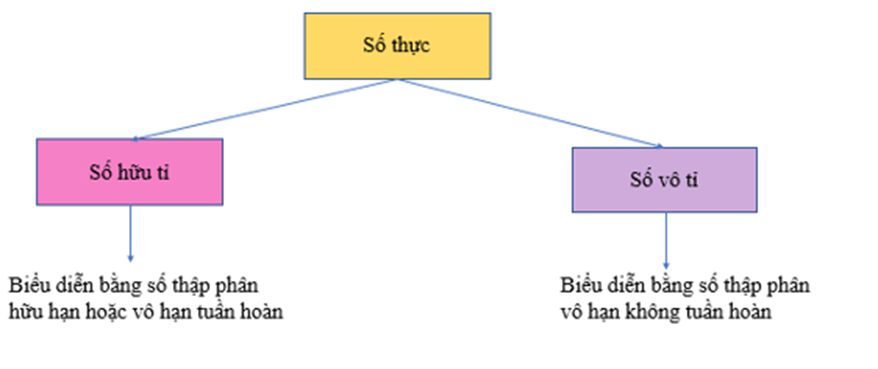
a) Các số hữu tỉ được biểu diễn bằng các số thập phân hữu hạn hoặc vô hạn tuần hoàn.

b) Các số vô tỉ được biểu diễn bằng các số thập phân vô hạn không tuần hoàn.

Lời giải bài tập Toán 7 Bài 2: Tập hợp R các số thực hay, chi tiết khác:

Hoạt động 3 trang 39 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 2: Tập hợp ℝ các số thực - Cánh diều

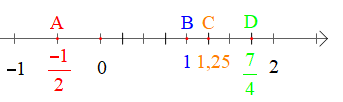
Hoạt động 3 trang 39 Toán lớp 7 Tập 1:Biểu diễn các số hữu tỉ sau trên trục số: $\frac{-1}{2}; 1; 1,25; \frac{7}{4}$.

Lời giải:

+ Biểu diễn số hữu tỉ $\frac{-1}{2}$

• Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm –1 đến điểm 0) thành hai phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng $\frac{1}{2}$ đơn vị cũ).

• Đi theo chiều ngược với chiều dương của trục số, bắt đầu từ điểm 0, ta lấy 1 đơn vị mới đến điểm A. Điểm A biểu diễn số hữu tỉ $\frac{-1}{2}$ (như hình vẽ).

+ Biểu diễn số hữu tỉ 1: Theo chiều dương của trục số, ta lấy 1 đơn vị đến điểm B. Điểm B biểu diễn số hữu tỉ 1. 

+ Biểu diễn số hữu tỉ 1,25:

• Viết số 1,25 dưới dạng phân số tối giản 1,25 = $\frac{125}{100}$ = $\frac{5}{4}$

• Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành bốn phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng $\frac{1}{4}$ đơn vị cũ).

• Đi theo chiều dương của trục số, bắt đầu từ điểm 0, ta lấy 5 đơn vị mới đến điểm C. Điểm C biểu diễn số hữu tỉ 1,25 (như hình vẽ).

+ Biểu diễn số hữu tỉ $\frac{7}{4}$

• Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành bốn phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng $\frac{1}{4}$ đơn vị cũ).

• Đi theo chiều dương của trục số, bắt đầu từ điểm 0, ta lấy 7 đơn vị mới đến điểm D. Điểm D biểu diễn số hữu tỉ $\frac{7}{4}$ (như hình vẽ).

Lời giải bài tập Toán 7 Bài 2: Tập hợp R các số thực hay, chi tiết khác:

Hoạt động 4 trang 39 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 2: Tập hợp ℝ các số thực - Cánh diều

Hoạt động 4 trang 39 Toán lớp 7 Tập 1: Đọc kĩ nội dung sau:

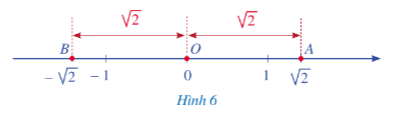
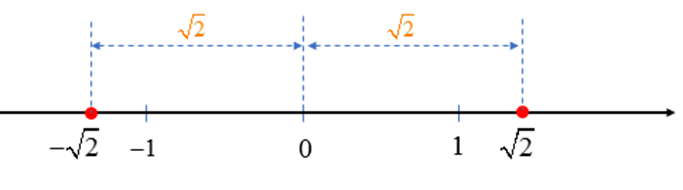
Gọi A là điểm (nằm bên phải điểm gốc 0) biểu diễn số thực $\sqrt{2}$ trên trục số nằm ngang. Gọi B là điểm nằm bên trái điểm gốc 0 sao cho OA = OB (điểm O biểu diễn điểm gốc 0). Khi đó, điểm B biểu diễn một số thực, kí hiệu là $-\sqrt{2}$ (Hình 6).

Hai điểm biểu diễn các số thực $\sqrt{2}$ và $-\sqrt{2}$ nằm về hai phía của điểm gốc 0 và cách đều điểm gốc 0.

Lời giải bài tập Toán 7 Bài 2: Tập hợp R các số thực hay, chi tiết khác:

Luyện tập 1 trang 40 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 2: Tập hợp ℝ các số thực - Cánh diều

Luyện tập 1 trang 40 Toán lớp 7 Tập 1: Tìm số đối của mỗi số sau: $\frac{2}{-9};-\mathrm{0,5};-\sqrt{3}$.

Lời giải:

Số đối của $\frac{2}{-9}$ là $\frac{2}{9}$.

Số đối của –0,5 là 0,5.

Số đối của $-\sqrt{3}$ là $\sqrt{3}.$

Lời giải bài tập Toán 7 Bài 2: Tập hợp R các số thực hay, chi tiết khác:

Hoạt động 5 trang 40 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 2: Tập hợp ℝ các số thực - Cánh diều

Hoạt động 5 trang 40 Toán lớp 7 Tập 1:

a) So sánh hai số thập phân sau: –0,617 và –0,614.

b) Nêu quy tắc so sánh hai số thập phân hữu hạn.

Lời giải:

a) Vì –0,617 và –0,614 là hai số thập phân âm nên ta đi so sánh hai số đối của chúng là 0,617 và 0,614.

Ta thấy phần nguyên của hai số cần so sánh đều là 0 nên ta chuyển sang so sánh phần thập phân của chúng.

Ta thấy ở hàng phần mười và hàng phần trăm của hai số này giống nhau nên ta so sánh đến hàng phần nghìn. 

Vì 7 > 4 nên 0,617 > 0,614 do đó –0,617 < –0, 614.

b) Quy tắc so sánh hai số thập phân hữu hạn.

- Nếu hai số thập phân hữu hạn a, b đem so sánh là hai số thập phân dương thì ta đi so sánh phần nguyên của chúng. Nếu phần nguyên bằng nhau thì ta so sánh đến phần thập phân, bắt đầu từ hàng phần mười, nếu hàng phần mười bằng nhau thì ta so sánh đến hàng phần trăm…đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì lớn hơn.

- Nếu hai số thập phân hữu hạn a, b đem so sánh có một số là số thập phân âm, một số là số thập phân dương thì số thập phân dương luôn lớn hơn số thập phân âm.

- Nếu hai số thập phân hữu hạn a, b đem so sánh là hai số thập phân âm thì ta so sánh hai số đối của chúng với nhau. Số nào có số đối lớn hơn thì nhỏ hơn.

Chú ý: Số thập phân âm luôn nhỏ hơn 0, số thập phân dương luôn lớn hơn 0.

Lời giải bài tập Toán 7 Bài 2: Tập hợp R các số thực hay, chi tiết khác:

Luyện tập 2 trang 41 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 2: Tập hợp ℝ các số thực - Cánh diều

Luyện tập 2 trang 41 Toán lớp 7 Tập 1: So sánh hai số thực sau: 

a) 1,(375) và $1\frac{3}{8}$;

b) –1,(27) và  –1,272.

Lời giải:

a) Ta có: $1\frac{3}{8}=\frac{11}{8}=\mathrm{1,375}=\mathrm{1,3750}$ và 1, (375) = 1, 375375…

Ta thấy kể từ trái sang phải, chữ số hàng phần mười, phần trăm, phần nghìn của hai số này giống nhau và cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số ở vị trí hàng phần chục nghìn.

Do 3 > 0 nên 1,375375… > 1,3750 hay 1,(375) > $1\frac{3}{8}$.

b) Ta có: –1,(27) = –1,2727… và –1,272 = –1,2720. 

Hai số này là hai số thập phân âm nên ta đi so sánh hai số đối của chúng.

Số đối của –1,2727… là 1,2727… 

Số đối của –1,2720 là 1,2720.

Ta thấy kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số ở vị trí hàng phần chục nghìn. 

Do 7 > 0 nên 1,2727… > 1,2720 do đó –1,2727… < –1,2720

Hay –1,(27) < –1,272.

Lời giải bài tập Toán 7 Bài 2: Tập hợp R các số thực hay, chi tiết khác:

Bài 1 trang 42 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 2: Tập hợp ℝ các số thực - Cánh diều

Bài 1 trang 42 Toán lớp 7 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) Nếu a $\in \mathbb{Z}$ thì a $\in ℝ$.

b) Nếu a $\in \mathbb{Q}$ thì a $\in ℝ$.

c) Nếu a $\in ℝ$ thì a $\in \mathbb{Z}$.

d) Nếu a $\in ℝ$ thì a $\notin \mathbb{Q}$.

Lời giải:

a) Nếu a ∈ ℤ thì a ∈ ℝ.

Nếu a ∈ ℤ tức a là số nguyên, mà mọi số nguyên đều là số thực, do đó a ∈ ℝ.

Vậy phát biểu a) đúng.

b) Nếu a ∈ ℚ thì a ∈ ℝ.

Nếu a ∈ ℚ tức a là số hữu tỉ, mà mọi số hữu tỉ đều là số thực a ∈ ℝ.

Vậy phát biểu b) đúng.

c) Nếu a ∈ ℝ thì a ∈ ℤ.

Nếu a ∈ ℝ tức a là số thực, mà không phải số thực nào cũng là số nguyên.

Chẳng hạn, 1,4 ∈ ℝ nhưng 1,4 ∉ ℤ.

Do đó phát biểu c) sai.

d) Nếu a ∈ ℝ thì a ∉ ℚ.

Nếu a ∈ ℝ tức a là số thực, mà không phải số thực nào cũng không phải là số hữu tỉ.

Chẳng hạn, $\frac{3}{3}$ ∈ ℝ nhưng $\frac{3}{3}$ ∈ ℚ

Do đó phát biểu d) sai.

Vậy, trong các phát biểu trên: Phát biểu đúng là a và b; Phát biểu sai là c và d.

Lời giải bài tập Toán 7 Bài 2: Tập hợp R các số thực hay, chi tiết khác:

Bài 2 trang 42 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 2: Tập hợp ℝ các số thực - Cánh diều

Bài 2 trang 42 Toán lớp 7 Tập 1: Tìm số đối của mỗi số sau:$\frac{-8}{35};\frac{5}{-6};-\frac{18}{7};\mathrm{1,15};-\mathrm{21,54};-\sqrt{7};\sqrt{5}$.

Lời giải:

Số đối của $\frac{-8}{35}$ là $\frac{8}{35}$.

Số đối của $\frac{5}{-6}$ là $\frac{5}{6}$.

Số đối của $-\frac{18}{7}$ là $\frac{18}{7}$.

Số đối của 1,15 là - 1,15.

Số đối của –21,54 là 21,54.

Số đối của $-\sqrt{7}$ là $\sqrt{7}$.

Số đối của $\sqrt{5}$ là $-\sqrt{5}$.

Lời giải bài tập Toán 7 Bài 2: Tập hợp R các số thực hay, chi tiết khác:

Bài 3 trang 42 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 2: Tập hợp R các số thực - Cánh diều

Bài 3 trang 42 Toán lớp 7 Tập 1 : So sánh:

a) –1,(81) và –1,812;

b) $2\frac{1}{7}$ và 2,142;

c) –48,075… và –48,275…;

d) $\sqrt{5}$ và $\sqrt{8}$

Lời giải:

a) Hai số cần so sánh là hai số âm nên ta đi so sánh số đối của chúng.

Số đối của –1,(81) là 1,(81). 

Số đối của –1,812 là 1,812.

Ta có: 1,(81) = 1, 8181…

So sánh: 1,8181…và 1,812 ta thấy: Kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số ở vị trí hàng phần nghìn. Mà 8 > 2 nên 1,8181… > 1,812. 

Do đó –1,8181… < –1,812 hay –1,(81) < -1,812.

b) Ta thấy $2\frac{1}{7}$ và 2,142 có phần nguyên giống nhau nên ta đi so sánh $\frac{1}{7}$ và 0,142.

Ta thực hiện đặt phép tính chia 1 cho 7 như sau:

Vậy $\frac{1}{7}=\mathrm{0,1428...}$

Ta so sánh 0,1428… và 0,1420

Kể từ trái sang phải, cặp số cùng hàng đầu tiên khác nhau là cặp chữ số hàng phần chục nghìn. Mà 8 > 0 nên 0,1428… > 0,1420 hay $\frac{1}{7}>\mathrm{0,142}$ nên $2\frac{1}{7}>\mathrm{2,142}$

c) Hai số cần so sánh là hai số âm nên ta đi so sánh hai số đối của chúng.

Số đối của –48,075… là 48,075… 

Số đối của –48,275… là 48,275… 

Ta so sánh 48,075…   và 48,275… 

Kể từ trái sang phải, cặp số cùng hàng đầu tiên khác nhau là cặp số hàng phần mười. Mà 0 < 2 nên 48,075… < 48,275…Do đó –48,075… > –48,275…

d) Vì 8 > 5 > 0 nên $\sqrt{8}>\sqrt{5}$.

Lời giải bài tập Toán 7 Bài 2: Tập hợp R các số thực hay, chi tiết khác:

Bài 4 trang 42 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 2: Tập hợp ℝ các số thực - Cánh diều

Bài 4 trang 42 Toán lớp 7 Tập 1: Tìm chữ số thích hợp cho $\boxed{?}$:

a) $-\mathrm{5,02}<-\mathrm{5,}\boxed{?}1$;

b) $-\mathrm{3,7}\boxed{?}8>-\mathrm{3,715}$;

c) $-\mathrm{0,5}\boxed{?}\left(742\right)<-\mathrm{0,59653}$;

d) $-\mathrm{1,}\left(4\boxed{?}\right)<-\mathrm{1,49}$.

Lời giải:

a) Vì $-\mathrm{5,02}<-\mathrm{5,}\boxed{?}1$ nên 5,02 > 5,$\boxed{?}$1 .

Ta xét hai số 5,02 và 5,$\boxed{?}$1 thấy phần nguyên của hai số giống nhau nên để số 5,02 > 5,$\boxed{?}$1 thì $\boxed{?}$ phải điền số 0 vì nếu là số lớn hơn 0 thì không thỏa mãn.

b) Vì $-\mathrm{3,7}\boxed{?}8>-\mathrm{3,715}$ nên 3,7$\boxed{?}$8 < 3,715. 

Ta xét hai số 3,7 8 và 3,715 thấy phần nguyên và hàng phần mười của hai số giống nhau; hàng phần nghìn có 8 > 5 nên hàng phần trăm của 3,7$\boxed{?}$8 phải nhỏ hơn hàng phần trăm của 3,715. 

Do đó $\boxed{?}$ chỉ có thể là 0.

c) Vì $-\mathrm{0,5}\boxed{?}\left(742\right)<-\mathrm{0,59653}$ nên 0,5$\boxed{?}$(742) > 0,59653. 

Ta xét hai số 0,5$\boxed{?}$(742) và 0,59653 thấy phần nguyên và hàng phần mười của hai số giống nhau nếu $\boxed{?}$ nhỏ hơn 9 thì 0,5$\boxed{?}$(742) < 0,58653 nên $\boxed{?}$ chỉ có thể là 9.

d) Vì $-\mathrm{1,}\left(4\boxed{?}\right)<-\mathrm{1,49}$ nên 1,$\left(4\boxed{?}\right)$ > 1,49

Ta có: $\mathrm{1,}\left(4\boxed{?}\right)=\mathrm{1,4}\boxed{?}4\boxed{?}\mathrm{...}$ ta thấy nếu $\boxed{?}$< 9 thì $\mathrm{1,}\left(4\boxed{?}\right)=\mathrm{1,4}\boxed{?}4\boxed{?}\mathrm{...}$< 1,49 nên $\boxed{?}$ chỉ có thể là 9.

Lời giải bài tập Toán 7 Bài 2: Tập hợp R các số thực hay, chi tiết khác:

Bài 5 trang 42 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 2: Tập hợp ℝ các số thực - Cánh diều

Bài 5 trang 42 Toán lớp 7 Tập 1:

a) Sắp xếp các số sau theo thứ tự tăng dần: 

–2,63…; 3,(3); –2,75…; 4,62.

b) Sắp xếp các số sau theo thứ tự giảm dần: 

1,371…; 2,065; 2,056…; –0,078…;1,(37).

Lời giải:

a) Nhận thấy trong các số trên thì có số thập phân dương và số thập phân âm và số thập phân âm luôn nhỏ hơn số thập phân dương.

Do đó ta chia thành các số trên thành hai nhóm để so sánh là nhóm số thập phân âm và nhóm số thập phân dương.

Nhóm 1: –2,63…; –2,75…

Nhóm 2: 3, (3); 4,62.

+) Xét nhóm 1: –2,63…; –2,75….

Đây là hai số thập phân âm nên ta so sánh số đối của chúng là 2,63… và 2,75…

Kể từ trái sang phải, cặp số cùng hàng đầu tiên khác nhau của hai số 2,63… và 2,75… là cặp số hàng phần mười. Mà 6 < 7 nên 2,63… < 2,75…. Do đó –2,63… > –2,75…

+) Xét nhóm 2: 3,(3); 4,62

Ta có 3,(3) = 3,33…

Kể từ trái sang phải, cặp số cùng hàng đầu tiên khác nhau của hai số 3,33…và 4,62 là cặp số hàng đơn vị. 

Mà 3 < 4 nên 3,33… < 4,62.

Sắp xếp các số theo thứ tự tăng dần: -2,75…; -2,63…; 3,(3); 4,62.

b) Ta thấy số thập phân âm bé hơn số thập phân dương nên –0,078 nhỏ nhất

Ta đi so sánh 1,371…; 2,065; 2,056…; 1,(37).

Vì 2 > 1 nên ta sẽ có những số có phần nguyên là 2 sẽ lớn hơn những số có phần nguyên là 1. 

Ta chia bốn số trên thành 2 nhóm để so sánh.

+) Nhóm 1 gồm 1,371… và 1,(37) = 1,3737…

Kể từ trái sang phải, cặp số cùng hàng đầu tiên khác nhau của hai số 1,371… và 1,3737… là cặp số hàng phần nghìn. 

Mà 3 > 1 nên 1,3737… > 1,371… 

Do đó 1,(37) > 1,371….

+) Nhóm 2 gồm 2,065 và 2,056….

Kể từ trái sang phải, cặp số cùng hàng đầu tiên khác nhau của hai số 2,065 và 2,056…. là cặp số hàng phần trăm mà 6 > 5 nên 2,065 > 2,056…

Sắp xếp các số theo thứ tự giảm dần: 2,065; 2,056…; 1,(37); 1,371…; –0,078…

Lời giải bài tập Toán 7 Bài 2: Tập hợp R các số thực hay, chi tiết khác:

Sách bài tập Toán 7 Bài 2: Tập hợp R các số thực - Cánh diều

Với giải sách bài tập Toán 7 Bài 2: Tập hợp R các số thực sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Bài 2.

Giải sách bài tập Toán 7 Bài 2: Tập hợp R các số thực - Cánh diều

Giải SBT Toán 7 trang 42 Tập 1

Vở bài tập Toán 7 Bài 2: Tập hợp R các số thực - Cánh diều

Với giải vở bài tập Toán lớp 7 Bài 2: Tập hợp R các số thực sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập về nhà trong VBT Toán 7 Bài 2.

Giải vở bài tập Toán 7 Bài 2: Tập hợp R các số thực - Cánh diều

I. Kiến thức trọng tâm

Giải VBT Toán 7 trang 37 Tập 1

Tập hợp R các số thực (Lý thuyết Toán lớp 7) - Cánh diều

Với tóm tắt lý thuyết Toán 7 Bài 2: Tập hợp R các số thực hay nhất, chi tiết sách Cánh diều sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Tập hợp R các số thực (Lý thuyết Toán lớp 7) - Cánh diều

Lý thuyết Tập hợp R các số thực

1. Tập hợp số thực

1.1 Số thực

- Số hữu tỉ và số vô tỉ được gọi chung là số thực.

- Tập hợp các số thực được kí hiệu là ℝ.

Ví dụ: Các số 1,2 ; $\frac{-5}{3}$ ; $\sqrt{5}$; … là các số thực.

1.2 Biểu diễn thập phân của số thực

- Mỗi số thực là số hữu tỉ hoặc số vô tỉ. Vì thế, mỗi số thực đều biểu diễn được dưới dạng số thập phân hữu hạn hoặc vô hạn. Ta có sơ đồ sau:

2. Biểu diễn số thực trên trục số

Tương tự như đối với số hữu tỉ, ta có thể biểu diễn mọi số thực trên trục số, khi đó điểm biểu diễn số thực x được gọi là điểm x.

Ví dụ: Biểu diễn các số thực sau trên trục số:

a) $\frac{-1}{2}$ và 2;

b) $\sqrt{2}$.

Hướng dẫn giải

a) Số $\frac{-1}{2}$ và 2 là hai số hữu tỉ, vì thế để biểu diễn hai số này trên trục số ta thực hiện như cách biểu diễn một số hữu tỉ trên trục số.

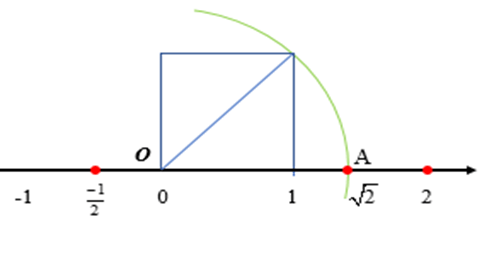
b) Số $\sqrt{2}$ là một số vô tỉ vì vậy để biểu diễn số $\sqrt{2}$ trên trục số ta làm như sau:

+ Vẽ một hình vuông với một cạnh là đoạn thẳng có hai đầu mút là điểm gốc 0 và điểm 1. Khi đó, đường chéo của hình vuông có độ dài cạnh bằng $\sqrt{2}$.

+ Vẽ một phần đường tròn tâm là điểm gốc 0, bán kính là $\sqrt{2}$, cắt trục số tại điểm A nằm bên phải gốc 0. Ta có OA = $\sqrt{2}$ và A là điểm biểu diễn $\sqrt{2}$.

Nhận xét:

- Không phải mỗi điểm trên trục số đều biểu diễn một số hữu tỉ. Vậy các điểm biểu diễn số hữu tỉ không lấp đầy trục số.

- Mỗi số thực được biểu diễn bởi một điểm trên trục số; Ngược lại, mỗi điểm trên trục số đều biểu diễn một số thực.

Vậy trục số còn được gọi là trục số thực.

3. Số đối của một số thực

- Trên trục số, hai số thực (phân biệt) có điểm biểu diễn nằm về hai phía của điểm gốc 0 và cách đều điểm gốc 0 được gọi là hai số đối nhau.

- Số đối của số thực a kí hiệu là – a.

- Số đối của số 0 là 0.

Nhận xét: Số đối của – a là số a, tức là –(–a) = a.
Ví dụ:

Số đối của số thực $\sqrt{2}$ là số thực $-\sqrt{2}$.

4. So sánh các số thực

4.1 So sánh hai số thực

Cũng như số hữu tỉ, trong hai số thực khác nhau luôn có một số nhỏ hơn số kia.

- Nếu số thực a nhỏ hơn số thực b thì ta biết a < b hay b > a.

- Số thực lớn hơn 0 gọi là số thực dương.

- Số thực nhỏ hơn 0 gọi là số thực âm.

- Số 0 không phải là số thực dương cũng không phải số thực âm.

- Nếu a < b và b < c thì a < c.

4.2 Cách so sánh hai số thực

- Ta có thể so sánh hai số thực bằng cách biểu diễn thập phân mỗi số thực đó rồi so sánh hai số thập phân đó.

- Việc biểu diễn một số thực dưới dạng số thập phân (hữu hạn hoặc vô hạn) thường là phức tạp. Trong một số trường hợp ta dùng quy tắc: Với a, b là hai số thực dương, nếu

a > b thì $\sqrt{a}>\sqrt{b}$.

Ví dụ: So sánh các số thực sau:

a) –1,(27) và –1,272 ;

b) $\sqrt{7}$ và $\sqrt{8}$.

Hướng dẫn giải

a) Ta viết –1,(27) = –1,27272727….. sau đó ta so sánh với –1,272.

Hai số –1,27272727… và –1,2720 có phần nguyên và đến hàng phần nghìn giống nhau, cặp chữ số khác nhau đầu tiên bắt đầu từ hàng phần chục nghìn.

Do 7 > 0 nên 1,27272727…..> 1,2720, suy ra –1,27272727…..< –1,2720.

Vậy –1,(27) < –1,272.

b) Ta có: 0 < 7 < 8 nên $\sqrt{7}$ < $\sqrt{8}$.

4.3 Minh họa trên trục số

Giả sử hai điểm x, y lần lượt biểu diễn hai số thực x, y trên trục số nằm ngang. Ta có nhận xét sau :

- Nếu x < y hay y > x thì điểm x nằm bên trái điểm y;

- Ngược lại nếu điểm x nằm bên trái điểm y thì x < y hay y > x.

Đối với hai điểm x, y lần lượt biểu diễn hai số thực x, y trên trục số thẳng đứng, ta cũng có nhận xét sau :

- Nếu x < y hay y > x thì điểm x nằm phía dưới điểm y;

- Ngược lại, nếu điểm x nằm phía dưới điểm y thì x < y hay y > x.

Ví dụ:

+ Vì $\frac{-3}{2}$ < –1 nên trên trục số nằm ngang, điểm $\frac{-3}{2}$nằm bên trái điểm –1.

+ Điểm $\sqrt{2}$ nằm bên trái điểm $\sqrt{5}$, vì vậy $\sqrt{2}$ < $\sqrt{5}$.

Bài tập Tập hợp R các số thực

Bài 1: Tìm số đối của mỗi số sau: $\frac{-5}{6}$; 1,25 ; $\sqrt{11}$; $-\sqrt{3}$.

Hướng dẫn giải

Số đối của số thực $\frac{-5}{6}$ là: $-\left(\frac{-5}{6}\right)=\frac{5}{6}$.

Số đối của số thực 1,25 là –1,25.

Số đối của $\sqrt{11}$ là $-\sqrt{11}$.

Số đối của số thực $-\sqrt{3}$ là $-(-\sqrt{3})=\sqrt{3}$.

Bài 2: So sánh

a) $2\frac{1}{7}$ và 2,142;

b) 3 và $\sqrt{8}$.

Hướng dẫn giải

a) Ta viết $2\frac{1}{7}=\frac{15}{7}=\mathrm{2,142857142857...}$. Và so sánh với số 2,1420

Ta thấy kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số ở vị trí hàng phần chục nghìn.

Do 8 > 0 nên 2,142857142857…> 2,1420. Vậy $2\frac{1}{7}$ > 2,142.

b) Ta có 3 > 0 và 3² = 9 nên $\sqrt{9}=3$. Để so sánh 3 và $\sqrt{8}$ ta sẽ so sánh $\sqrt{9}$ và $\sqrt{8}$.

Ta có 9 > 8 > 0 nên $\sqrt{9}$ > $\sqrt{8}$. Suy ra 3 > $\sqrt{8}$.

Học tốt Tập hợp R các số thực

Các bài học để học tốt Tập hợp R các số thực Toán lớp 7 hay khác:

15 Bài tập Tập hợp R các số thực (có đáp án) - Cánh diều Trắc nghiệm Toán 7

Với 15 bài tập trắc nghiệm Tập hợp R các số thực Toán lớp 7 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Cánh diều sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 7.

15 Bài tập Tập hợp R các số thực (có đáp án) - Cánh diều Trắc nghiệm Toán 7

Câu 1. Phát biểu nào sau đây là sai?

A. Nếu a là số nguyên thì a cũng là số thực;

B. Nếu a là số tự nhiên thì a không phải là số vô tỉ;

C. Số 0 là số thực dương.

D. Tập hợp các số thực được kí hiệu là ℝ.

Câu 2. Phát biểu nào sau đây là đúng?

A. Mọi số thực đều là số vô tỉ;

B. Mỗi số hữu tỉ đều là số vô tỉ;

C. Mọi số thực đều là số hữu tỉ;

D. Số thực có thể là số vô tỉ hoặc số hữu tỉ.

Câu 3. Cho các phát biểu sau:

(I) Số thực dương lớn hơn số thực âm.

(II) Số 0 là số thực dương.

(III) Số thực dương là số tự nhiên.

(IV) Số nguyên âm là số thực.

Số phát biểu sai là:

A. 1;

B. 2;

C. 3;

D. 4.

Câu 4. Chọn cách viết sai.

A. $\frac{3}{2}\in \mathbb{Q};$

B. $\frac{2}{3}\in ℝ;$

C. $1,\left(02\right)\in ℝ;$

D. $\sqrt{2}\in \mathbb{Q}.$

Câu 5. Cho các phát biểu sau:

(I) Mỗi số thực đều được biểu diễn bởi một điểm trên trục số.

(II) Mỗi điểm trên trục số đều biểu diễn một số hữu tỉ.

(III) Các điểm biểu diễn số thực lấp đầy trục số.

(IV) Trục số cũng được gọi là trục số thực.

Các phát biểu đúng là:

A. (I), (II) và (III);

B. (II), (III) và (IV);

C. (I), (III) và (IV);

D. (I), (II) và (IV).

Câu 6. Số đối của số $\sqrt{3}$ là:

A. $\sqrt{3}$ ;

B. -$\sqrt{3}$;

C. $\frac{1}{\sqrt{3}}$;

D. -$\frac{1}{\sqrt{3}}$ .

Câu 7. Điền từ còn thiếu hợp lí vào phát biểu sau: “Trên trục số, hai số thực (phân biệt) có điểm biểu diễn nằm về hai phía của điểm gốc 0 và cách đều điểm gốc 0 được gọi là …”

A. hai số bằng nhau;

B. hai số khác nhau;

C. hai số nghịch đảo;

D. hai số đối nhau.

Câu 8. Số đối của $-\frac{\sqrt{5}}{2}$ là:

A. $-\frac{\sqrt{5}}{2}$;

B. $\frac{\sqrt{5}}{2}$;

C. $\frac{2}{\sqrt{5}};$

D. $-\frac{2}{\sqrt{5}}.$

Câu 9. Trên trục số nằm ngang, điểm M và N lần lượt biểu biễn hai số thực m và n. Nếu m < n thì:

A. Điểm M nằm bên trái điểm N;

B. Điểm M nằm bên phải điểm N;

C. Điểm M nằm phía dưới điểm N;

D. Điểm M nằm phía trên điểm N.

Câu 10. So sánh hai số a = 0,123456…. và b = 0,(123) ta được:

A. a < b;

B. a = b;

C. a > b;

D. Không so sánh được.

Câu 11. Cho hai số $a=-\sqrt{0,1416}$ và $b=-\sqrt{0,1461}$. So sánh hai số a và b ta được:

A. a < b;

B. a = b;

C. a > b;

D. Không so sánh được.

Câu 12. Chữ số thích hợp điền cho $?$ trong phép so sánh $-95,\left(112\right)<-95,?12112$ là:

A. 0;

B. 1;

C. 2;

D. 3.

Câu 13. Sắp xếp các số $-\frac{1}{3};0,5;-\sqrt{2};2,1;-1$ theo thứ tự tăng dần là:

A. $-\frac{1}{3};0,5;-\sqrt{2};2,1;-1$;

B. $-\frac{1}{3};-\sqrt{2};-1;0,5;2,1;$

C. $-\sqrt{2};-1;-\frac{1}{3};0,5;2,1;$

D. $-1;-\sqrt{2};-\frac{1}{3};0,5;2,1.$

Câu 14. Cho x² = 5 thì giá trị x là:

A. $-\sqrt{5}$;

B. $\sqrt{5}$;

C. $-\sqrt{5}$ hoặc $\sqrt{5}$;

D. 25.

Câu 15. Giá trị của biểu thức $0,5.\sqrt{64}-\frac{1}{5}.{\left(\sqrt{5}\right)}^2$là:

A. 3;

B. $\frac{1}{3}$;

C. - $\frac{1}{3}$;

D. $\frac{1}{3}$.

Xem thêm bài tập trắc nghiệm Toán lớp 7 Cánh diều có đáp án hay khác: