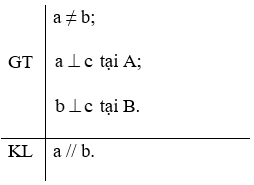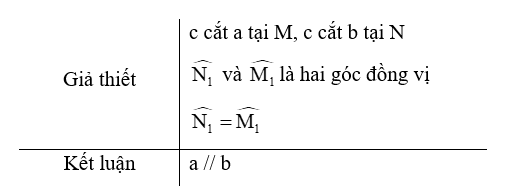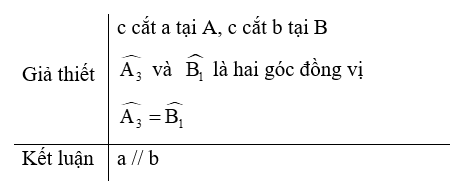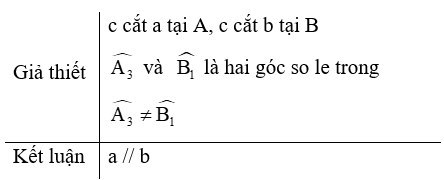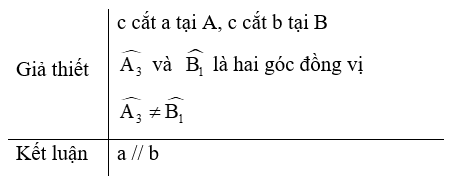Với giải bài tập Toán 7 Bài 4: Định lí sách Cánh diều hay nhất, chi tiết giúp học sinh lớp 7 dễ dàng làm bài tập Toán Hình 7 Bài 4.

Giải Toán 7 Cánh diều Bài 4: Định lí

Video Giải Toán 7 Bài 4: Định lí - Cô Ngô Thị Vân (Giáo viên VietJack)

Hoạt động khởi động

Giải Toán 7 trang 105 Tập 1

Khởi động trang 105 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 4: Định lý - Cánh diều

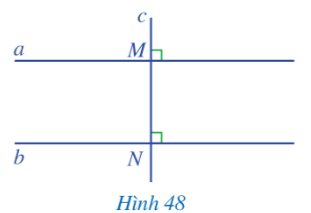
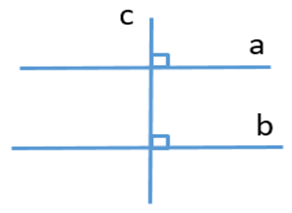
Khởi động trang 105 Toán lớp 7 Tập 1: Bạn Ánh vẽ hai đường thẳng a, b cùng vuông góc với đường thẳng c (Hình 48) và khẳng định với bạn Ngân rằng: “Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng khác thì hai đường thẳng đó song song với nhau”.

Câu khẳng định có dạng “Nếu … thì …” trong toán học được gọi là gì?

Lời giải:

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

Câu khẳng định có dạng “Nếu … thì …” trong toán học được gọi là một định lí.

Lời giải bài tập Toán 7 Bài 4: Định lí hay, chi tiết khác:

Hoạt động 1 trang 105 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 4: Định lý - Cánh diều

Hoạt động 1 trang 105 Toán lớp 7 Tập 1: Đọc kĩ nội dung sau.

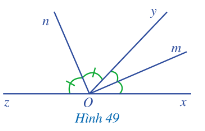
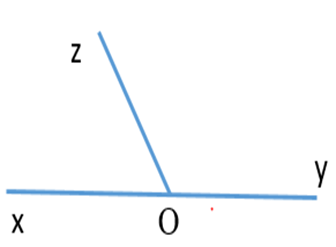
Cho hai góc kề bù là xOy và yOz, Om và On lần lượt là tia phân giác của góc xOy và góc yOz (Hình 49).

Ta thấy $\widehat{mOy}=\frac{1}{2}\widehat{xOy}$ và $\widehat{yOn}=\frac{1}{2}\widehat{yOz}$ , suy ra:

$\widehat{mOn}=\widehat{mOy}+\widehat{yOn}=\frac{1}{2}\widehat{xOy}+\frac{1}{2}\widehat{yOz}$

$=\frac{1}{2}\left(\widehat{xOy}+\widehat{yOz}\right)=\frac{1}{2}.180°={90}^o.$

Như vậy, có thể khẳng định: “Nếu một góc có hai cạnh là hai tia phân giác của hai góc kề bù thì góc đó là góc vuông”.

Lời giải:

Học sinh đọc kĩ các nội dung của hoạt động.

Lời giải bài tập Toán 7 Bài 4: Định lí hay, chi tiết khác:

Hoạt động 2 trang 105 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 4: Định lý - Cánh diều

Hoạt động 2 trang 105 Toán lớp 7 Tập 1: Xét khẳng định “Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng khác thì hai đường thẳng đó song song với nhau”, ta thấy: Khẳng định này được phát biểu ở dạng “Nếu … thì …”. Trong khẳng định đó, hãy nêu:

- Phần nằm giữa hai từ “Nếu” và từ “thì”;

- Phần nằm sau từ “thì”.

Lời giải:

- Phần nằm giữa hai từ “Nếu” và từ “thì” là “hai đường thẳng phân biệt cùng vuông góc với một đường thẳng khác”;

- Phần nằm sau từ “thì” là “hai đường thẳng đó song song với nhau”.

Lời giải bài tập Toán 7 Bài 4: Định lí hay, chi tiết khác:

Luyện tập 1 trang 106 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 4: Định lý - Cánh diều

Luyện tập 1 trang 106 Toán lớp 7 Tập 1: Viết giả thiết và kết luận của định lí: “Nếu một đường thẳng c cắt hai đường thẳng a, b và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng a, b song song với nhau”.

Lời giải:

- Giả thiết: một đường thẳng c cắt hai đường thẳng a, b và trong số các góc tạo thành có một cặp góc so le trong bằng nhau.

- Kết luận: hai đường thẳng a, b song song với nhau.

Lời giải bài tập Toán 7 Bài 4: Định lí hay, chi tiết khác:

Hoạt động 3 trang 106 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 4: Định lý - Cánh diều

Hoạt động 3 trang 106 Toán lớp 7 Tập 1: Cho định lí:

“Nếu hai góc đối đỉnh thì hai góc đó bằng nhau”.

a) Vẽ hình minh họa nội dung định lí trên.

b) Viết giả thiết và kết luận của định lí trên.

c) Chứng tỏ định lí trên là đúng.

Lời giải:

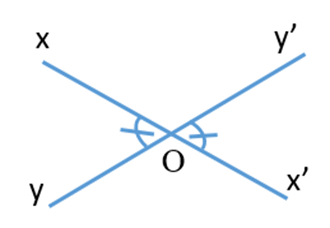
a) Giả sử hai đường thẳng xx’ và yy’ cắt nhau tại điểm O.

Khi đó, hai góc xOy và góc x’Oy’ là hai góc đối đỉnh.

Ta có hình vẽ sau:

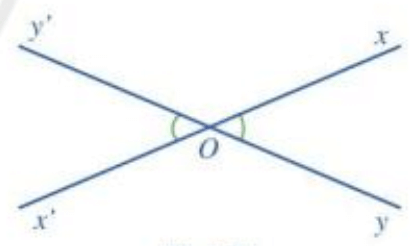
b) Giả thiết và kết luận của định lí:

- Giả thiết: Hai góc xOy và x’Oy’ là hai góc đối đỉnh.

- Kết luận: $\widehat{xOy}=\widehat{x\text{'}Oy\text{'}}$.

c) Do góc xOy và góc x’Oy’ là hai góc đối đỉnh nên Oy và Oy’ là hai tia đối nhau.

Suy ra $\widehat{xOy}$ và $\widehat{xOy\text{'}}$ là hai góc kề bù nên:

$\widehat{xOy}+\widehat{xOy\text{'}}={180}^o$  (1)

Tương tự, ta có: 

$\widehat{xOy\text{'}}+\widehat{x\text{'}Oy\text{'}}={180}^o$  (2)

Từ (1) và (2) ta suy ra: $\widehat{xOy}+\widehat{xOy\text{'}}=\widehat{xOy\text{'}}+\widehat{x\text{'}Oy\text{'}}$

Vậy $\widehat{xOy}=\widehat{x\text{'}Oy\text{'}}$

Lời giải bài tập Toán 7 Bài 4: Định lí hay, chi tiết khác:

Luyện tập 2 trang 107 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 4: Định lý - Cánh diều

Luyện tập 2 trang 107 Toán lớp 7 Tập 1: Chứng minh định lí: Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc so le trong bằng nhau.

Lời giải:

Giả sử đường thẳng c cắt hai đường thẳng phân biệt a, b lần lượt tại hai điểm A và B.

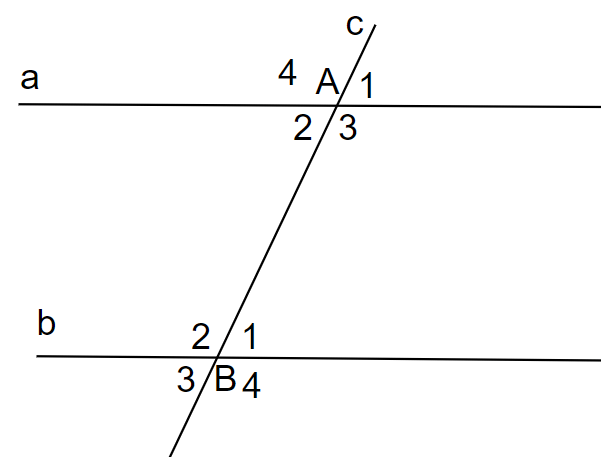
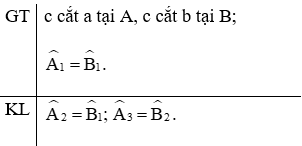
Ta có: ${\widehat{A}}_1={\widehat{A}}_2$ (hai góc đối đỉnh)

${\widehat{A}}_1={\widehat{B}}_1$ (GT)

Suy ra ${\widehat{A}}_2={\widehat{B}}_1$ (cùng bằng $\widehat{A_1}$).

Tương tự, ta chứng minh được các cặp góc so le trong còn lại bằng nhau.

Từ đó ta có điều phải chứng minh.

Lời giải bài tập Toán 7 Bài 4: Định lí hay, chi tiết khác:

Bài 1 trang 107 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 4: Định lý - Cánh diều

Bài 1 trang 107 Toán lớp 7 Tập 1: Vẽ hình minh họa và viết giả thiết, kết luận cho mỗi định lí sau:

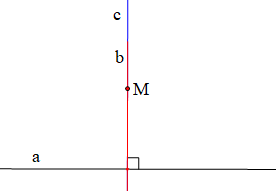
a) Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.

b) Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng khác thì chúng song song với nhau.

c) Nếu hai đường thẳng cùng đi qua một điểm và cùng vuông góc với một đường thẳng khác thì hai đường thẳng đó trùng nhau.

Lời giải:

a) Định lí “Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại”.

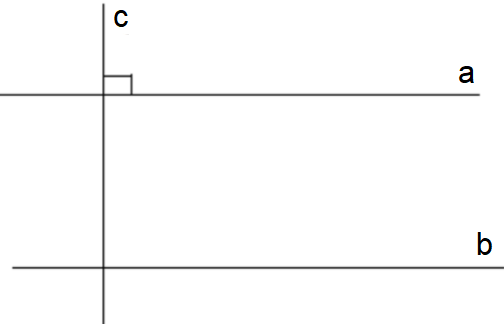
b) Định lí “Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng khác thì chúng song song với nhau”.

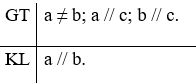
c) Định lí “Nếu hai đường thẳng cùng đi qua một điểm và cùng vuông góc với một đường thẳng khác thì hai đường thẳng đó trùng nhau”.

Lời giải bài tập Toán 7 Bài 4: Định lí hay, chi tiết khác:

Bài 2 trang 107 Toán 7 Tập 1 Cánh diều

Giải Toán 7 Bài 4: Định lý - Cánh diều

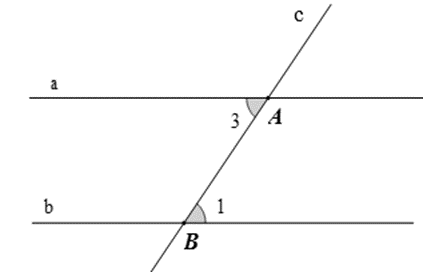
Bài 2 trang 107 Toán lớp 7 Tập 1: Cho định lí: “Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng khác thì hai đường thẳng đó song song với nhau”.

a) Vẽ hình minh họa nội dung định lí trên.

b) Viết giả thiết, kết luận của định lí trên.

c) Chứng minh định lí trên.

Lời giải:

Định lí “Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng khác thì hai đường thẳng đó song song với nhau”.

a) Ta có hình vẽ:

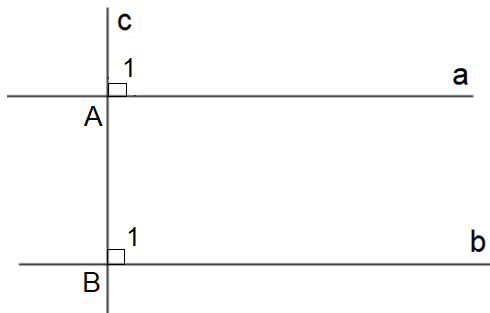
b) Giả thiết, kết luận của định lí:

c) Chứng minh định lí:

Ta có: a ⊥ c  tại A nên ${\widehat{A}}_1={90}^o$; 

b ⊥ c tại B nên ${\widehat{B}}_1={90}^o$

Khi đó, ${\widehat{A}}_1={\widehat{B}}_1={90}^o$.

Mà ${\widehat{A}}_1$ và ${\widehat{B}}_1$ ở vị trí đồng vị.

Do đó a // b.

Lời giải bài tập Toán 7 Bài 4: Định lí hay, chi tiết khác:

Sách bài tập Toán 7 Bài 4: Định lý - Cánh diều

Với giải sách bài tập Toán 7 Bài 4: Định lý sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Bài 4.

Giải sách bài tập Toán 7 Bài 4: Định lý - Cánh diều

Giải SBT Toán 7 trang 113 Tập 1

Vở bài tập Toán 7 Bài 4: Định lí - Cánh diều

Với giải vở bài tập Toán lớp 7 Bài 4: Định lí sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập về nhà trong VBT Toán 7 Bài 4.

Giải vở bài tập Toán 7 Bài 4: Định lí - Cánh diều

I. Kiến thức trọng tâm

Giải VBT Toán 7 trang 106 Tập 1

Định lí (Lý thuyết Toán lớp 7) - Cánh diều

Với tóm tắt lý thuyết Toán 7 Bài 4: Định lí hay nhất, chi tiết sách Cánh diều sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Định lí (Lý thuyết Toán lớp 7) - Cánh diều

Lý thuyết Định lí

1. Định lý

Khẳng định có các tính chất sau thì được gọi là định lý:

- Là một phát biểu về một tính chất toán học;

- Tính chất toán học đó đã được chứng tỏ là đúng không dựa vào trực giác hay đo đạc,..

Nhận xét:

+ Định lý thường được phát biểu dưới dạng “Nếu … thì …”.

+ Phần nằm giữa từ “Nếu” và từ “thì” là phần giả thiết, phần nằm sau từ “thì” là phần kết luận.

Ví dụ: Định lý: “Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau”.

Giả thiết: Một đường thẳng cắt hai đường thẳng song song.

Kết luận: Hai góc so le trong bằng nhau.

Ta có thể vẽ hình minh họa và viết GT, KL của định lý này như sau:

2. Chứng minh định lý

Chứng minh định lý là một tiến trình lập luận từ giả thiết suy ra kết luận là đúng.

Ví dụ: Chứng minh định lý: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”.

Hướng dẫn giải

Chứng minh

Ta có a ⊥ c suy ra $\widehat{A_1}={90}^0$; và b ⊥ c suy ra $\widehat{B_1}={90}^0$.

Suy ra $\widehat{A_1}=\widehat{B_1}$.

Mà hai góc $\widehat{A_1}$, $\widehat{B_1}$ là hai góc đồng vị.

Vậy a // b.

Bài tập Định lí

Bài 1: Vẽ hình minh họa và viết giả thiết, kết luận bằng kí hiệu cho định lý sau: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường còn lại”.

Hướng dẫn giải

Bài 2: Cho định lý : “Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau”.

a) Vẽ hình minh họa nội dung định lý trên.

b) Viết giả thiết, kết luận của định lý trên.

c) Chứng minh định lý trên.

Hướng dẫn giải

a)

b)

c) Chứng minh

Qua điểm B kẻ đường thẳng b’ sao cho góc $\widehat{B_2}=\widehat{A_1}$.

Khi đó đường thẳng c tạo với hai đường thẳng a và b’ hai góc đồng vị bằng nhau.

Theo dấu hiệu nhận biết hai đường thẳng song song, ta có a và b’ song song với nhau.

Suy ra qua B có hai đường thẳng b, b’ cùng song song với a.

Theo Tiên đề Euclid thì hai đường thẳng b’ và b trùng nhau.

Từ đó suy ra $\widehat{B_1}=\widehat{A_1}$ (vì cùng bằng $\widehat{B_2}$).

Học tốt Định lí

Các bài học để học tốt Định lí Toán lớp 7 hay khác:

15 Bài tập Định lí (có đáp án) - Cánh diều Trắc nghiệm Toán 7

Với 15 bài tập trắc nghiệm Định lí Toán lớp 7 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Cánh diều sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 7.

15 Bài tập Định lí (có đáp án) - Cánh diều Trắc nghiệm Toán 7

Câu 1. Định lí thường được phát biểu dưới dạng:

A. Thì … là…;

B. Nếu … thì …;

C. Vì … nên …;

D. Do … nên ….

Câu 2. Phát biểu định lý sau thành lời:

A. Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau;

B. Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng vuông góc với nhau;

C. Nếu một đường thẳng cắt hai đường thẳng phân biệt thì chúng song song với nhau;

D. Nếu một đường thẳng cắt hai đường thẳng phân biệt thì chúng vuông góc với nhau.

Câu 3. Định lí: “Nếu hai đường thẳng song song cùng cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau”. Giả thiết của định lí là:

A. a // b; a // c;

B. a // c; b bất kì;

C. a // b; $a\perp c$;

D. $a//b;c\cap a=\left(M\right);c\cap b=\left(N\right)$.

Câu 4. Chọn phát biểu đúng

A. Giả thiết của định lí là điều suy ra;

B. Kết luận của định lí là điều cho biết;

C. Giả thiết của định lí là điều cho biết;

D. Cả A và B đều đúng.

Câu 5. Điền vào chỗ trống những nội dung thích hợp để được định lí đúng.

Nếu … thì $NA=NB=\frac{1}{2}AB$.

A. N thuộc AB;

B. N là trung điểm của AB;

C. N nằm giữa AB;

D. Cả 3 đáp án trên đều sai.

Câu 6. Điền vào chỗ trống nội dung thích hợp.

“Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành một cặp góc đồng vị bằng nhau thì hai đường thẳng ….”

A. a, b song song với nhau;

B. a, b vuông góc với nhau;

C. a, b cắt nhau;

D. a, b trùng nhau.

Câu 7. Điền vào chỗ trống: “Nếu một đường thẳng cắt hai đường thẳng song song thì …”

A. Hai góc đồng vị bằng nhau;

B. Hai góc so le trong bằng nhau;

C. Hai góc kề bù bằng nhau;

D. Cả A và B đều đúng.

Câu 8. Cho định lí: “Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại”.

Hình vẽ minh hoạ cho định lí trên là:

A.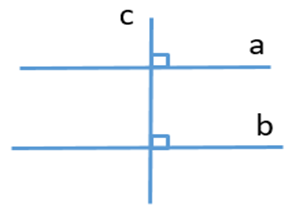

B.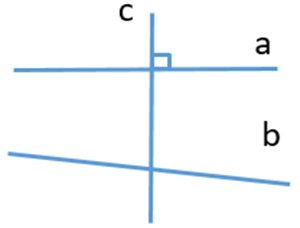

C.

D.

Câu 9. Viết giả thiết cho định lí sau:

“Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng khác thì hai đường thẳng đó song song với nhau”.

A. Giả thiết:a ≠b; a // c, b // c;

B. Giả thiết: a ≡b; a // b, b // c;

C. Giả thiết: $a\equiv b;a\perp c,b//c$;

D. Giả thiết: $a\ne b;a\perp c,b//c$.

Câu 10. Điền vào chỗ trống.

Nếu hai góc đối đỉnh thì ….

A. hai góc đó có tổng số đo bằng 180°;

B. hai góc đó không bằng nhau;

C. hai góc đó bằng nhau;

D. hai góc đó có hiệu số đo bằng 180°.

Câu 11. Trong định lí, phần nằm giữa từ “Nếu” và từ “thì” là phần giả thiết vậy phần nằm sau từ “thì” là phần?

A. kết luận;

B. trả lời;

C. ý nghĩa;

D. định nghĩa.

Câu 12. Phát biểu định lí sau bằng lời.

A. Nếu một đường thẳng c cắt hai đường thẳng a, b và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì hai đường thẳng a, b vuông góc với nhau;

B. Nếu một đường thẳng c cắt hai đường thẳng a, b và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì hai đường thẳng a, b song song với nhau;

C. Nếu một đường thẳng c cắt hai đường thẳng a, b và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng a, b song song với nhau;

D. Nếu một đường thẳng c cắt hai đường thẳng a, b và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng a, b vuông góc với nhau.

Câu 13. Vẽ hình minh họa nội dung định lí sau:

“Nếu hai góc đối đỉnh thì hai góc đó bằng nhau”

A.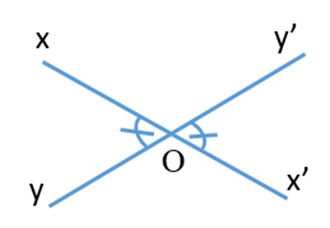

B.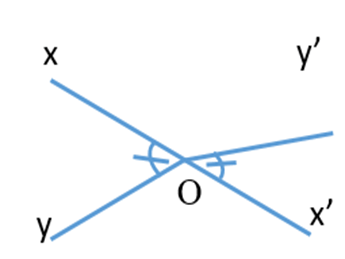

C.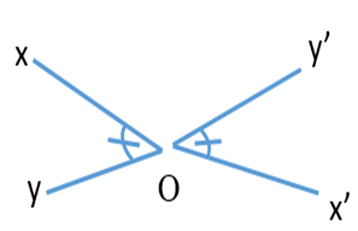

D.

Câu 14. Viết giả thiết, kết luận cho định lí sau:

“Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song với nhau.”

A.A

B.

C.

D.

Câu 15. Chứng minh định lí là:

A. Dùng lập luận để từ giả thiết suy ra kết luận;

B. Dùng hình vẽ để từ giả thiết suy ra kết luận;

C. Dùng đo đạc thực tế để từ giả thiết suy ra kết luận;

D. Cả 3 đáp án đều đúng.

Xem thêm bài tập trắc nghiệm Toán lớp 7 Cánh diều có đáp án hay khác: