Giải Toán 7 | No tags
Với giải bài tập Toán 7 Bài 8: Đường vuông góc và đường xiên sách Cánh diều hay nhất, chi tiết giúp học sinh lớp 7 dễ dàng làm bài tập Toán Hình 7 Bài 8.
Video Giải Toán 7 Bài 8: Đường vuông góc và đường xiên - Cô Ngô Thị Vân (Giáo viên VietJack)
Hoạt động khởi động
Khởi động trang 97 Toán lớp 7 Tập 2: Đường vuông góc và đường xiên có tính chất như thế nào?
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Lời giải:
Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
Lời giải bài tập Toán 7 Bài 8: Đường vuông góc và đường xiên hay, chi tiết khác:
Luyện tập 1 trang 97 Toán lớp 7 Tập 2: Cho tam giác ABC vuông tại A.
a) Khoảng cách từ điểm B đến đường thẳng AC bằng độ dài đoạn thẳng nào?
b) Đoạn thẳng nào là một đường xiên kẻ từ điểm B đến đường thẳng AC?
Lời giải:
a) Khoảng cách từ điểm B đến đường thẳng AC bằng độ dài đoạn thẳng BA.
b) Đoạn thẳng BC là một đường xiên kẻ từ B đến đường thẳng AC.
Lời giải bài tập Toán 7 Bài 8: Đường vuông góc và đường xiên hay, chi tiết khác:
Hoạt động trang 98 Toán lớp 7 Tập 2: Giả sử AH, AB lần lượt là đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng d (Hình 80).
Trong tam giác AHB, hãy so sánh:
a) Số đo góc AHB và số đo góc ABH.
b) Độ dài cạnh AB và độ dài cạnh AH.
Lời giải:
a) Tam giác AHB có là góc vuông nên là góc lớn nhất trong tam giác AHB.
Do đó .
b) Độ dài cạnh AB lớn hơn độ dài cạnh AH.
Lời giải bài tập Toán 7 Bài 8: Đường vuông góc và đường xiên hay, chi tiết khác:
Luyện tập 2 trang 98 Toán lớp 7 Tập 2: Cho tam giác nhọn ABC, . Gọi H là hình chiếu của A trên BC. Sắp xếp các đoạn thẳng AB, AH, AC theo thứ tự độ dài tăng dần.
Lời giải:
Tam giác ABH vuông tại H nên là góc lớn nhất trong tam giác ABH.
Do đó cạnh AB là cạnh lớn nhất trong tam giác ABH.
Suy ra AH < AB (1).
Tam giác ABC có nên AC > AB (2).
Từ (1) và (2) ta có AH < AB < AC.
Thứ tự độ tăng dần các đoạn thẳng AB, AH, AC là AH; AB; AC.
Lời giải bài tập Toán 7 Bài 8: Đường vuông góc và đường xiên hay, chi tiết khác:
Bài 1 trang 99 Toán lớp 7 Tập 2: Chỉ ra các đường vuông góc, các đường xiên kẻ từ điểm I trong Hình 83a và từ điểm C trong Hình 83b.
Lời giải:
+) Xét Hình 83a:
Đường vuông góc kẻ từ điểm I đến đường thẳng d là IH.
Các đường xiên kẻ từ điểm I đến đường thẳng d là IM và IN.
+) Xét Hình 83b:
Đường vuông góc kẻ từ C đến đường thẳng Ox là CA.
Đường xiên kẻ từ C đến đường thẳng Ox là CO.
Đường vuông góc kẻ từ C đến đường thẳng Oy là CB.
Đường xiên kẻ từ C đến đường thẳng Oy là CO.
Lời giải bài tập Toán 7 Bài 8: Đường vuông góc và đường xiên hay, chi tiết khác:
Bài 2 trang 99 Toán lớp 7 Tập 2: Quan sát Hình 84 và cho biết:
a) Khoảng cách từ điểm O đến đường thẳng a;
b) Khoảng cách từ điểm O đến đường thẳng b;
c) Khoảng cách từ điểm O đến đường thẳng c.
Lời giải:
a) Khoảng cách từ điểm O đến đường thẳng a bằng 1 cm.
b) Khoảng cách từ điểm O đến đường thẳng b bằng 2 cm.
c) Khoảng cách từ điểm O đến đường thẳng c bằng 3 cm.
Lời giải bài tập Toán 7 Bài 8: Đường vuông góc và đường xiên hay, chi tiết khác:
Bài 3 trang 99 Toán lớp 7 Tập 2: Cho tam giác nhọn ABC.
a) Vẽ H là hình chiếu của B trên đường thẳng AC.
b) Vẽ K là hình chiếu của H trên đường thẳng AB.
c) Chứng minh rằng: HK < BH < BC.
Lời giải:
a) Ta có hình vẽ sau:
b) Ta có hình vẽ sau:
c) Xét ∆BKH vuông tại K nên là góc lớn nhất trong ∆BKH.
Do đó BH là cạnh lớn nhất trong ∆BKH.
Suy ra HK < BH (1).
Xét ∆BHC vuông tại H có là góc lớn nhất trong ∆BHC.
Do đó BC là cạnh lớn nhất trong ∆BHC.
Suy ra BH < BC (2).
Từ (1) và (2) suy ra HK < BH < BC.
Lời giải bài tập Toán 7 Bài 8: Đường vuông góc và đường xiên hay, chi tiết khác:
Bài 4 trang 99 Toán lớp 7 Tập 2: Trong một thí nghiệm khoa học, bạn Duy đặt hai chiếc đũa thủy tinh, một chiếc dài 14 cm và một chiếc dài 30 cm vào một bình thủy tinh có dạng hình trụ đựng dung dịch, cả hai đũa đều chạm đáy bình. Đường kính của đáy bình là 12 cm, chiều cao của dung dịch trong bình là 15 cm (bỏ qua bề dày của bình). Hỏi bạn Duy có thể cầm vào chiếc đũa thủy tinh nào mà ngón tay không bị chạm vào dung dịch? Vì sao?
Lời giải:
Ta thấy 12 < 14 < 15 nên chiếc đũa dài 14 cm bị chìm hoàn toàn trong dung dịch.
30 > 15 > 12 nên chiếc đũa dài 30 cm còn một đầu không bị chìm trong dung dịch.
Do đó bạn Duy có thể cầm vào chiếc đũa dài 30 cm thì ngón tay không bị chạm vào dung dịch.
Lời giải bài tập Toán 7 Bài 8: Đường vuông góc và đường xiên hay, chi tiết khác:
Bài 5 trang 99 Toán lớp 7 Tập 2: Hình 85b mô tả mặt cắt đứng của một chiếc thang chữ A (Hình 85a), trong đó độ dài của một bên thang được tính bằng độ dài đoạn thẳng OM, chiều cao của chiếc thang được tính bằng độ dài đoạn OH, với H là hình chiếu của điểm O trên đường thẳng d. Một người sử dụng thang này có thể đứng ở độ cao 4 m hay không nếu độ dài của một bên thang là 3,5 m? Vì sao?
Lời giải:
∆OMH vuông tại H nên là góc lớn nhất trong tam giác OMH.
Do đó OM là cạnh lớn nhất trong tam giác OMH.
Khi đó OM > OH hay 3,5 > OH.
Vậy người sử dụng thang này không thể đứng ở độ cao 4 m so với mặt đất.
Lời giải bài tập Toán 7 Bài 8: Đường vuông góc và đường xiên hay, chi tiết khác:
Với giải sách bài tập Toán 7 Bài 8: Đường vuông góc và đường xiên sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Bài 8.
Với giải vở bài tập Toán lớp 7 Bài 8: Đường vuông góc và đường xiên sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập về nhà trong VBT Toán 7 Bài 8.
I. Kiến thức trọng tâm
Với tóm tắt lý thuyết Toán 7 Bài 8: Đường vuông góc và đường xiên hay nhất, chi tiết sách Cánh diều sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.
1. Đường vuông góc và đường xiên
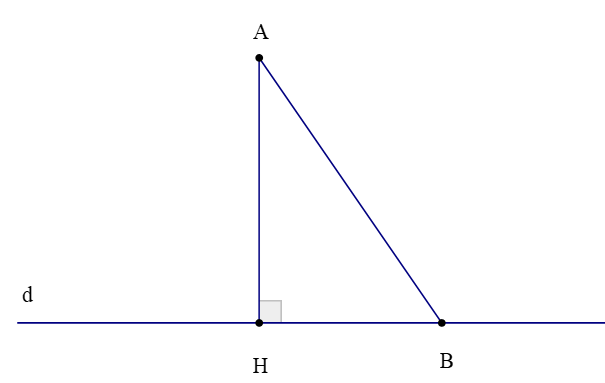
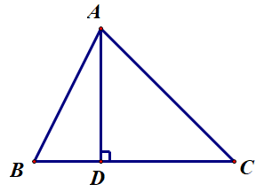
Trong hình vẽ trên, ta gọi:
– Đoạn thẳng AH là đoạn vuông góc hay đường vuông góc kẻ từ điểm A đến đường thẳng d;
– Điểm H là chân của đường vuông góc hay hình chiếu của điểm A trên đường thẳng d;
– Độ dài đoạn thẳng AH là khoảng cách từ điểm A đến đường thẳng d;
– Đoạn thẳng AB là một đường xiên kẻ từ điểm A đến đường thẳng d.
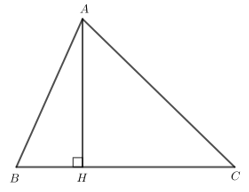
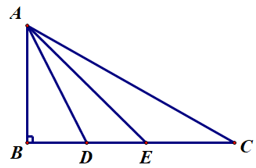
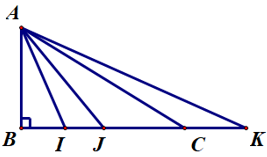
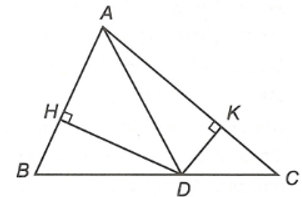
Ví dụ: Quan sát hình vẽ dưới đây:
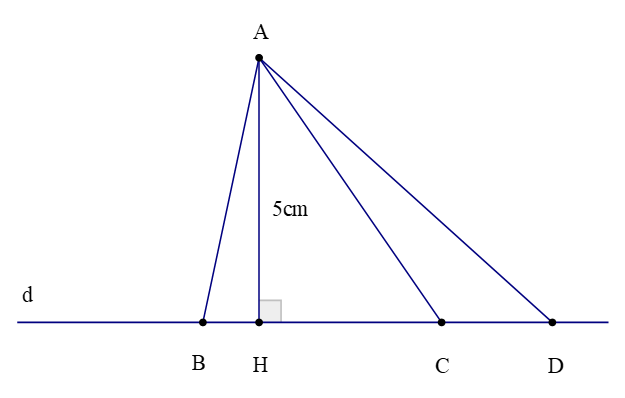
Hãy cho biết:
a) Hình chiếu của điểm A trên đường thẳng d; khoảng cách từ điểm A đến đường thẳng BD bằng độ dài đoạn thẳng nào?
b) Đoạn thẳng nào là đường xiên kẻ từ điểm A đến đường thẳng d?
Hướng dẫn giải
a) Vì AH vuông góc với đường thẳng d tại H do đó:
Hình chiếu của điểm A trên đường thẳng d là điểm H.
Khoảng cách từ điểm A đến đường thẳng BD là AH = 5cm (do BD ≡ d).
b) Các đoạn thẳng AB; AC; AD là các đường xiên kẻ từ A đến đường thẳng d.
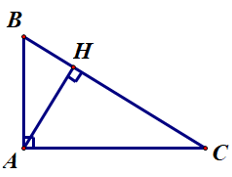
2. Quan hệ giữa đường vuông góc và đường xiên
– Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
Ví dụ: Qua điểm O nằm ngoài đường thẳng a kẻ đường thẳng vuông góc với đường thẳng a và cắt a tại B. Lấy hai điểm A và C nằm trên đường thẳng a và nằm về hai phía so với điểm B sao cho ; So sánh độ dài các đoạn thẳng OA; OB; OC.
Hướng dẫn giải
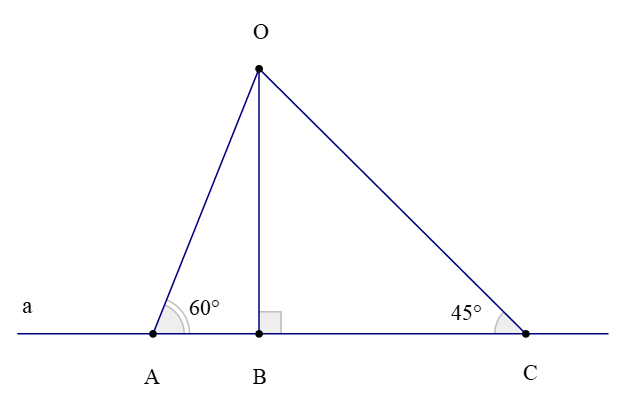
Vì OB là đường vuông góc kẻ từ điểm O đến đường thẳng a và OA; OC là các đường xiên kẻ từ O đến đường thẳng a nên OB là đoạn thẳng ngắn nhất
Do đó OB < OA; OB < OC (1)
Xét ∆OAC có (vì 60° > 45°)
Suy ra: OC > OA (quan hệ giữa góc và cạnh đối diện trong tam giác) (2)
Từ (1) và (2) suy ra: OB < OA < OC.
Vậy OB < OA < OC.
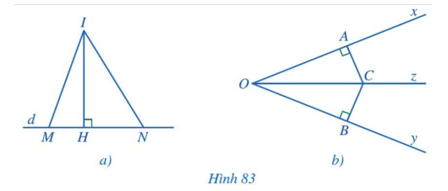
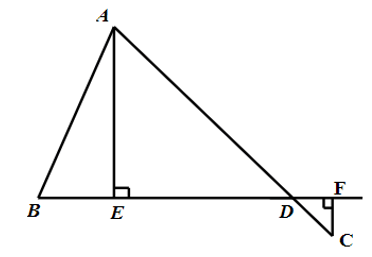
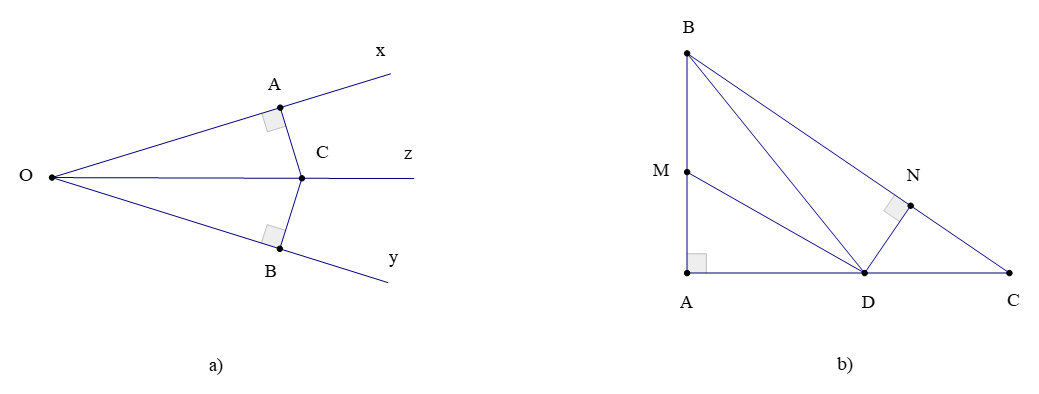
Bài 1. Trong mỗi hình sau, chỉ ra các đường vuông góc, các đường xiên kẻ từ điểm C (hình a) và từ điểm D (hình b) (nếu có):
Hướng dẫn giải
– Quan sát hình a ta có:
Đường vuông góc kẻ từ điểm C tới Ox là CA vì CA ⊥ Ox tại A;
Đường vuông góc kẻ từ điểm C tới Oy là CB vì CB ⊥ Oy tại B;
Đoạn thẳng CO là đường xiên kẻ từ điểm C đến tia Ox và tia Oy.
– Quan sát hình b ta có:
Đường vuông góc kẻ từ điểm D tới BA là DA vì DA ⊥ AB tại A;
Đường vuông góc kẻ từ điểm D tới BC là DN vì DN ⊥ BC tại N;
Đoạn thẳng DM là đường xiên kẻ từ D tới AB;
Đoạn thẳng DC là đường xiên kẻ từ D tới BC;
Đoạn thẳng DB là đường xiên kẻ từ D tới AB và BC.
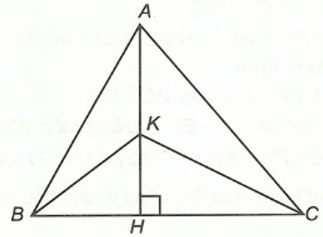
Bài 2. Cho tam giác ABC có AH, BK, CL là các đường cao kẻ từ các đỉnh tương ứng. Chứng minh rằng: AH + BK + CL < AB + BC + CA.
Hướng dẫn giải:
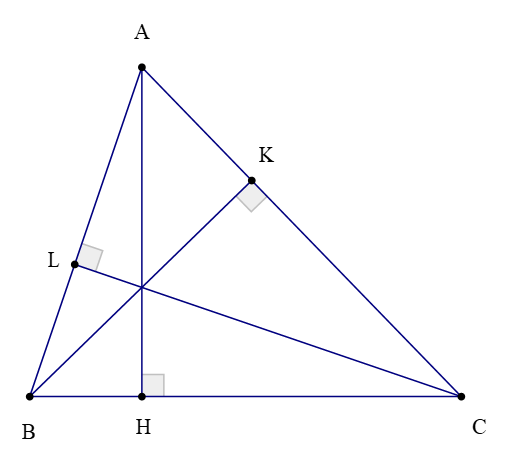
+) Ta có:
• AH là đường vuông góc;
• AB, AC là các đường xiên kẻ từ A tới BC.
Do đó nên AH + AH < AB + AC
Hay 2AH < AB + AC
Suy ra AH < (1)
+) Ta có BK là đường vuông góc và BA, BC là các đường xiên kẻ từ B tới AC.
Do đó nên 2BK < BA + BC
Suy ra BK < (2)
+) Ta có CL là đường vuông góc và CB, CA là các đường xiên kẻ từ B tới AB.
Do đó nên 2CL < CA + CB
Suy ra CL < (3)
Từ (1) (2) và (3) suy ra:
AH + BK + CL < + +
Suy ra AH + BK + CL <
AH + BK + CL <
Hay AH + BK + CL < AB + BC + CA.
Vậy AH + BK + CL < AB + BC + CA.
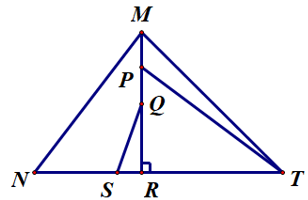
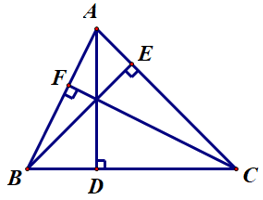
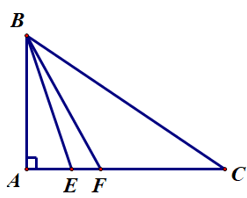
Bài 3.Cho ∆ABC vuông tại A, M là trung điểm của AC. Gọi D, E lần lượt là hình chiếu của A và C trên đường thẳng BM. So sánh BD + BE và 2AB.
Hướng dẫn giải
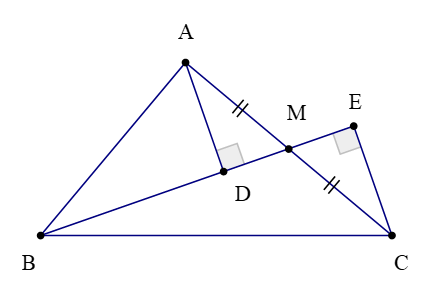
Vì D, E lần lượt là hình chiếu của A và C trên đường thẳng BM
Nên AD ⊥ BM tại D suy ra
Và CE ⊥ BM tại E suy ra
Xét ∆ADM và ∆CEM có:
AM = CM (vì M là trung điểm của AC),
(hai góc đối đỉnh).
Suy ra ∆ADM = ∆CEM (cạnh huyền – góc nhọn)
Do đó DM = EM (hai cạnh tương ứng)
Ta có: BD + BE
= BD + (BM + ME)
= (BD + ME) + BM
Mà DM = ME (chứng minh trên)
Nên BD + BE = (BD + DM) + BM
= BM + BM = 2BM (1)
Vì ∆ABM có (do DABC vuông tại A) nên ∆ABM vuông tại A.
Suy ra BM > AB (vì trong tam giác vuông thì cạnh huyền là cạnh lớn nhất).
Hay 2BM > 2AB (2)
Từ (1) và (2) suy ra BD + BE = 2BM > 2AB.
Vậy BD + BE > 2AB.
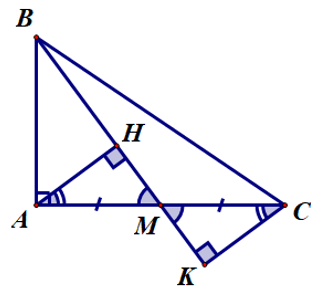
Bài 4. Cho ∆ABC có , AC < BC, kẻ CH ⊥ AB tại H. Trên các cạnh AB và AC lấy tương ứng hai điểm M và N sao cho BM = BC, CN = CH. Chứng minh rằng:
a) MN ⊥ AC;
b) AC + BC < AB + CH.
Hướng dẫn giải
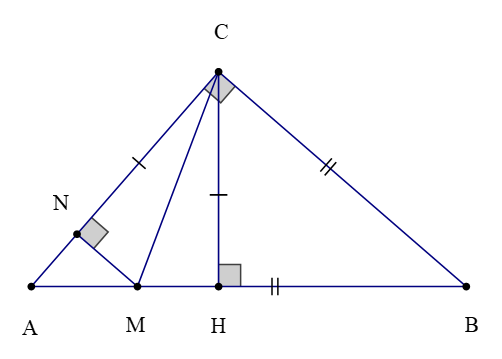
Xét ∆BMC có BM = BC (giả thiết) nên ∆BMC cân tại B.
Suy ra (tính chất tam giác cân) (1)
Vì CH ⊥ AB tại H nên ∆CHM vuông tại H.
Suy ra (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Hay (2)
Từ (1) và (2) suy ra (3)
Ta có (vì ∆ABC vuông tại C) (4)
Từ (3) và (4) suy ra:
Xét ∆NCM và ∆HCM có:
CN = CH (giả thiết),
(chứng minh trên),
CM là cạnh chung.
Suy ra ∆NCM = ∆HCM (c.g.c)
Suy ra (hai góc tương ứng)
Do đó MN ⊥ AC tại N.
Vậy MN ⊥ AC.
b) Ta có AB + CH = AM + MB + CH
Mà BM = BC; CH = CN (giả thiết)
Do đó AB + CH = AM + BC + CN (5)
Theo phần a ta có: MN ⊥ AC tại N nên ∆ANM vuông tại N.
Do đó cạnh huyền AM là cạnh lớn nhất.
Suy ra AM > AN.
Hay AM + CN > AN + CN
Suy ra AM + CN > AC
Do đó AM + CN + BC > AC + BC (6)
Từ (5) và (6) suy ra: AB + CH > AC + BC
Vậy AC + BC < AB + CH.
Các bài học để học tốt Đường vuông góc và đường xiên Toán lớp 7 hay khác:
Với 15 bài tập trắc nghiệm Đường vuông góc và đường xiên Toán lớp 7 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Cánh diều sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 7.
Câu 1. Cho hình bên.
Độ dài đoạn thẳng nào ngắn nhất?
A. AB;
B. AD;
C. AE;
D. AC.
Câu 2. Trong hình bên có bao nhiêu đường xiên kẻ từ các điểm M, P, Q đến đường thẳng NT?
A. 2;
B. 3;
C. 4;
D. 5.
Câu 3. Cho ∆ABC có AD là đường cao như hình bên.
Trong ba cạnh AB, AD, AC, cạnh nào ngắn nhất?
A. AD;
B. AB;
C. AC;
D. Không thể so sánh được.
Câu 4. Cho ∆ABC vuông tại A. Kẻ AH ⊥ BC (H ∈ BC). Có bao nhiêu đường vuông góc kẻ từ các điểm A, B, C đến các đường thẳng có trong hình bên?
A. 3;
B. 4;
C. 5;
D. 7.
Câu 5. Cho ∆ABC vuông tại B. Trên đường thẳng BC lấy điểm I, J, K sao cho AI < AJ < AK. Hỏi B là hình chiếu của các điểm nào lên đường thẳng AB?
A. C, J, A, K;
B. A, C, K, J;
C. I, J, C, A;
D. I, J, C, K.
Câu 6. Cho ∆ABC (AB < AC), đường cao AH (H ∈ BC). Lấy điểm K bất kì thuộc AH (K ≠ H). Trong các đoạn thẳng AB, AC, AH, BK, CK, KH, đoạn thẳng nào ngắn nhất?
A. AH;
B. KH;
C. BK;
D. CK.
Câu 7. Cho ∆ABC, điểm D nằm giữa B và C. Gọi H, K lần lượt là chân các đường vuông góc kẻ từ điểm D xuống các đường thẳng AB, AC.
So sánh BC và tổng DH + DK.
A. DH + DK > BC;
B. DH + DK < BC;
C. DH + DK = BC;
D. Không thể so sánh được.
Câu 8. Cho ∆ABC có , . Gọi H là chân đường vuông góc kẻ từ B. Khẳng định nào sau đây đúng?
A. HA > AC;
B. HA < AC;
C. HA = AC;
D. .
Câu 9. Cho ∆ABC. Vẽ AD ⊥ BC, BE ⊥ AC, CF ⊥ AB (D ∈ BC, E ∈ AC, F ∈ AB). So sánh AD + BE + CF và chu vi C của ∆ABC.
A. AD + BE + CF = C;
B. AD + BE + CF < C;
C. AD + BE + CF > C;
D. Không thể so sánh được.
Câu 10. Cho ∆MNP vuông tại M. Vẽ MH ⊥ NP tại H. Trên cạnh NP lấy điểm E sao cho NE = MN. Trên cạnh MP lấy điểm F sao cho MF = MH. Khoảng cách từ E đến đường thẳng MP là đoạn thẳng:
A. EM;
B. EF;
C. EP;
D. EN.
Câu 11. Cho ∆ABC vuông tại A. Trên cạnh AB lấy điểm E, trên cạnh AC lấy điểm F. So sánh độ dài các cạnh EA và BF.
A. EA = BF;
B. EA < BF;
C. EA > BF;
D. Không thể so sánh được.
Câu 12. Cho hình vẽ bên.
So sánh AC và AE + CF.
A. AC > AE + CF;
B. AC < AE + CF;
C. AC = AE + CF;
D. Không thể so sánh được.
Câu 13. Cho ∆ABC vuông tại A, biết AB = 10 cm. Trên đường thẳng AC, lấy hai điểm E và F sao cho AE = 3 cm, AF = 5 cm. So sánh CA, CB, CE và CF.
A. CF < CE < CA < CB;
B. CB < CF < CA < CE;
C. CE < CA < CB < CF;
D. CF < CA < CE < CB.
Câu 14. Cho ∆ABC vuông tại A. Gọi M là trung điểm AC. Kẻ AH ⊥ BM tại H, CK ⊥ BM tại K. So sánh AB và .
A. ;
B. ;
C. ;
D. Không thể so sánh được.
Câu 15. Hình bên mô tả một chiếc thang đứng hình chữ A là tam giác ABC. Do chiếc thang hơi ngắn nên một người thợ đã nối thêm 2 thanh gỗ bằng nhau BM và CN lần lượt vào hai cạnh AB, AC. Để giữ thăng bằng và cố định chiếc thang nên người thợ này muốn đóng thêm 2 thanh gỗ bằng nhau là BN và CM. Biết BC = 0,6 m, MN = 0,9 m. Em hãy cho biết độ dài thanh gỗ BN cần dài ít nhất bao nhiêu là hợp lí?
A. 0,3 m;
B. 0,6 m;
C. 0,75 m;
D. 0,8 m.
Xem thêm bài tập trắc nghiệm Toán lớp 7 Cánh diều có đáp án hay khác:
