Với giải bài tập Toán 7 Bài 1: Góc và cạnh của một tam giác sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh lớp 7 dễ dàng làm bài tập Toán Hình 7 Bài 1.

Giải Toán 7 Chân trời sáng tạo Bài 1: Góc và cạnh của một tam giác

Hoạt động khởi động

Giải Toán 7 trang 44 Tập 2

Khởi động trang 44 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 1: Góc và cạnh của một tam giác - Chân trời sáng tạo

Khởi động trang 44 Toán 7 Tập 2:

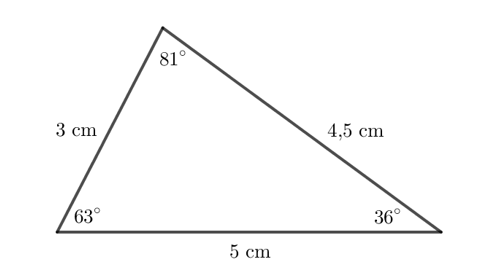
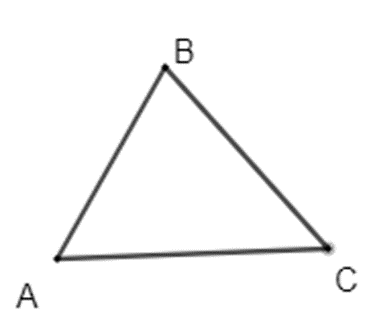
- Hãy đo ba góc và ba cạnh của tam giác trong hình bên.

- Em có nhận xét gì về tổng số đo của ba góc trong tam giác này?

- Hãy so sánh tổng độ dài hai cạnh với độ dài cạnh còn lại.

Lời giải:

Sử dụng thước có vạch chia và thước đo góc ta thu được các số đo như sau:

- Tổng số đo ba góc trong tam giác này bằng 81° + 63° + 36° = 180°.

- Ta thấy 2,6 + 4 > 4,4;

4 + 4,4 > 2,6;

4,4 + 2,6 > 4.

Vậy tổng độ dài hai cạnh của tam giác lớn hơn cạnh còn lại của tam giác.

Lời giải bài tập Toán 7 Bài 1: Góc và cạnh của một tam giác hay, chi tiết khác:

Khám phá 1 trang 44 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 1: Góc và cạnh của một tam giác - Chân trời sáng tạo

Khám phá 1 trang 44 Toán 7 Tập 2:

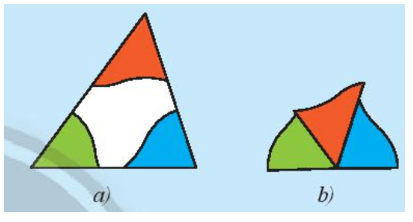
a) Cắt một tấm bìa hình tam giác và tô màu ba góc của nó (Hình 1a). Cắt rời ba góc ra khỏi tam giác rồi đặt ba góc kề nhau (Hình 1b).

Em hãy dự đoán tổng số đo của ba góc trong Hình 1b.

b) Chứng minh tính chất về tổng số đo ba góc trong một tam giác theo gợi ý sau:

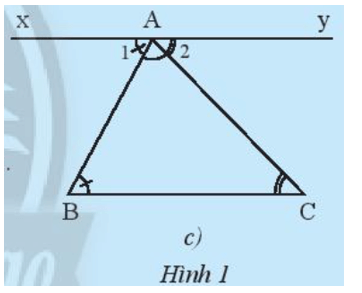
Qua A kẻ đường thẳng xy song song với BC như Hình 1c.

Ta có: xy // BC $\Rightarrow \hat{B}$= ? (so le trong) (1)

và $\hat{C}$= ? (so le trong) (2)

Từ (1) và (2) suy ra: $\hat{B}+\widehat{BAC}+\hat{C}={\hat{A}}_1+\widehat{BAC}+{\hat{A}}_2=\widehat{xAy}=?$

Lời giải:

a) Dự đoán tổng số đo ba góc trong Hình 1b bằng 180°.

b) Qua A kẻ đường thẳng xy song song với BC như Hình 1c.

Ta có: xy // BC $\Rightarrow \hat{B}$= ${\hat{A}}_1$(so le trong) (1)

và $\hat{C}$= ${\hat{A}}_2$(so le trong) (2)

Từ (1) và (2) suy ra: $\hat{B}+\widehat{BAC}+\hat{C}={\hat{A}}_1+\widehat{BAC}+{\hat{A}}_2=\widehat{xAy}=180°$.

Lời giải bài tập Toán 7 Bài 1: Góc và cạnh của một tam giác hay, chi tiết khác:

Thực hành 1 trang 45 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 1: Góc và cạnh của một tam giác - Chân trời sáng tạo

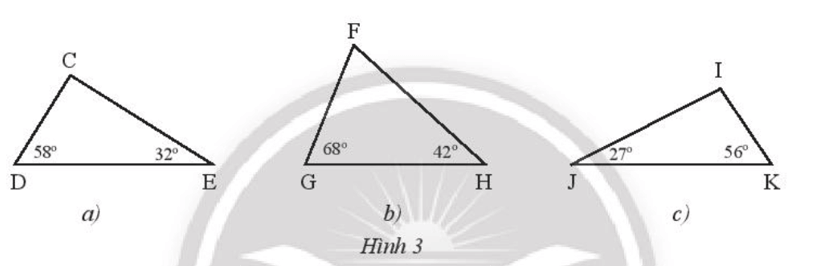
Thực hành 1 trang 45 Toán 7 Tập 2: Tìm số đo các góc chưa biết của các tam giác trong Hình 3 và cho biết tam giác nào là tam giác nhọn, tam giác nào là tam giác tù, tam giác nào là tam giác vuông.

Lời giải:

Xét △CDE có $\hat{C}=180°-\hat{D}-\hat{E}$= 180^o - 58^o - 32^o = 90^o.

△CDE có $\hat{C}=90°$nên △CDE vuông tại C.

Xét △FGH có $\hat{F}=180°-\hat{G}-\hat{H}$= 180^o - 68^o - 42^o = 70^o.

DFGH có số đo ba góc đều nhỏ hơn 90^o nên △FGH là tam giác nhọn.

Xét △IJK có $\hat{I}=180°-\hat{J}-\hat{K}$= 180^o - 27^o - 56^o = 97^o.

△IJK có $\hat{I}=97°>90°$nên △IJK là tam giác tù.

Vậy △CDE là tam giác vuông, △FGH là tam giác nhọn, △IJK là tam giác tù.

Lời giải bài tập Toán 7 Bài 1: Góc và cạnh của một tam giác hay, chi tiết khác:

Khám phá 2 trang 45 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 1: Góc và cạnh của một tam giác - Chân trời sáng tạo

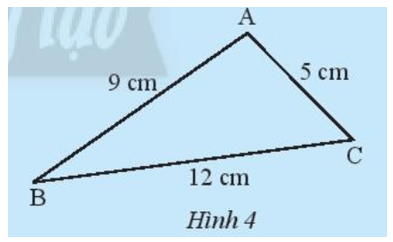
Khám phá 2 trang 45 Toán 7 Tập 2: Hãy so sánh tổng độ dài hai cạnh của tam giác trong Hình 4 với độ dài cạnh còn lại.

Lời giải:

Ta thấy: 9 + 5 > 12 nên AB + AC > BC.

5 + 12 > 9 nên AC + BC > AB.

12 + 9 > 5 nên BC + AB > AC.

Vậy tổng độ dài hai cạnh của tam giác lớn hơn cạnh còn lại của tam giác.

Lời giải bài tập Toán 7 Bài 1: Góc và cạnh của một tam giác hay, chi tiết khác:

Thực hành 2 trang 46 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 1: Góc và cạnh của một tam giác - Chân trời sáng tạo

Thực hành 2 trang 46 Toán 7 Tập 2: Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác?

a) 7 cm; 8 cm; 11 cm;

b) 7 cm; 9 cm; 16 cm;

c) 8 cm; 9 cm; 16 cm.

Lời giải:

a) Ta thấy 11 < 7 + 8 nên bộ ba độ dài 7 cm; 8 cm; 11 cm có thể là độ dài ba cạnh của một tam giác.

b) Ta thấy 16 = 7 + 9 nên bộ ba độ dài 7 cm; 9 cm; 16 cm không thể là độ dài ba cạnh của một tam giác.

c) Ta thấy 16 < 8 + 9 nên bộ ba độ dài 8 cm; 9 cm; 16 cm có thể là độ dài ba cạnh của một tam giác.

Lời giải bài tập Toán 7 Bài 1: Góc và cạnh của một tam giác hay, chi tiết khác:

Vận dụng trang 46 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 1: Góc và cạnh của một tam giác - Chân trời sáng tạo

Vận dụng trang 46 Toán 7 Tập 2: Cho tam giác ABC với độ dài ba cạnh là ba số nguyên. Nếu biết AB = 5 cm, AC = 3 cm thì cạnh BC có thể có độ dài là bao nhiêu xăngtimét?

Lời giải:

Trong tam giác ABC ta có:

AB - AC < BC < AB + AC hay 5 - 3 < BC < 5 + 3.

Do đó 2 < BC < 8.

Mà độ dài cạnh BC là một số nguyên nên BC có thể nhận các giá trị 3 cm; 4 cm; 5 cm; 6 cm; 7 cm.

Lời giải bài tập Toán 7 Bài 1: Góc và cạnh của một tam giác hay, chi tiết khác:

Bài 1 trang 46 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 1: Góc và cạnh của một tam giác - Chân trời sáng tạo

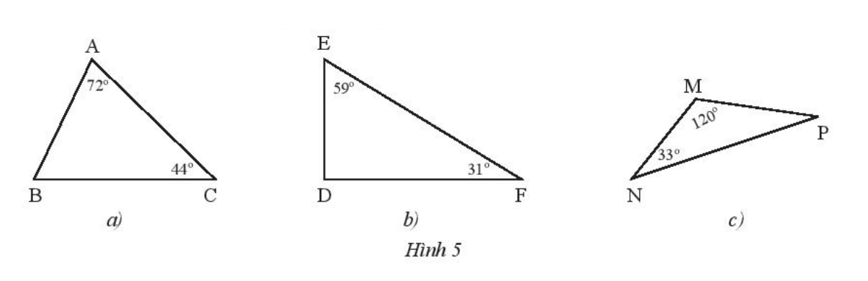
Bài 1 trang 46 Toán 7 Tập 2: Tìm số đo các góc chưa biết của các tam giác trong Hình 5.

Lời giải:

Áp dụng định lí về tổng ba góc trong một tam giác ta có:

Xét tam giác ABC: $\hat{B}=180°-\hat{A}-\hat{C}$= 180^o - 72^o - 44^o = 64^o.

Xét tam giác DEF: $\hat{D}=180°-\hat{E}-\hat{F}$= 180^o - 59^o - 31^o = 90^o.

Xét tam giác MNP: $\hat{P}=180°-\hat{M}-\hat{N}$= 180^o - 120^o - 33^o = 27^o.

Lời giải bài tập Toán 7 Bài 1: Góc và cạnh của một tam giác hay, chi tiết khác:

Bài 2 trang 47 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 1: Góc và cạnh của một tam giác - Chân trời sáng tạo

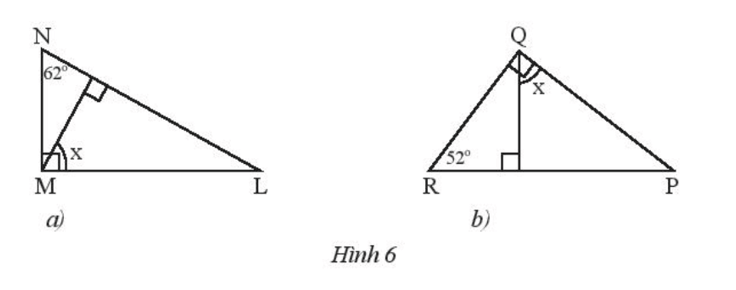
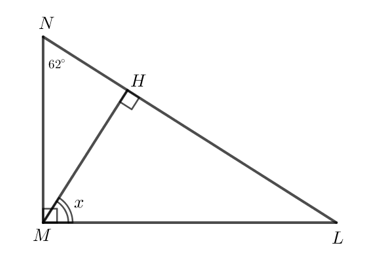
Bài 2 trang 47 Toán 7 Tập 2: Tính số đo x của góc trong Hình 6.

Lời giải:

- Xét Hình 6a:

Kẻ MH vuông góc với LN tại H.

Xét tam giác NML vuông tại M:

$\hat{N}+\hat{L}=90°$(trong tam giác vuông, tổng hai góc nhọn bằng 90^o).

Do đó $\hat{L}=90°-\hat{N}$= 90^o - 62^o = 28^o.

Xét tam giác MLH vuông tại H:

x + $\hat{L}$= 90^o (trong tam giác vuông, tổng hai góc nhọn bằng 90^o).

Do đó x = 90^o - $\hat{L}$= 90^o - 28^o = 62^o.

Vậy x = 62^o.

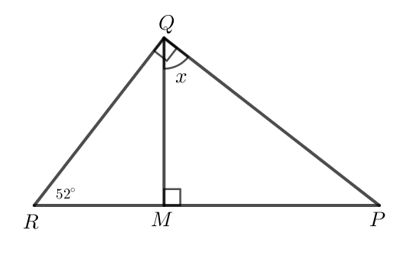
- Xét Hình 6b:

Xét tam giác QRP vuông tại Q:

$\hat{R}+\hat{P}=90°$(trong tam giác vuông, tổng hai góc nhọn bằng 90^o).

Do đó $\hat{P}=90°-\hat{R}$= 90^o - 52^o = 38^o.

Xét tam giác QMP vuông tại M:

x + $\hat{P}$= 90^o (trong tam giác vuông, tổng hai góc nhọn bằng 90^o).

Do đó x = 90^o - $\hat{P}$= 90^o - 38^o = 52^o.

Vậy x = 52^o.

Lời giải bài tập Toán 7 Bài 1: Góc và cạnh của một tam giác hay, chi tiết khác:

Bài 3 trang 47 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 1: Góc và cạnh của một tam giác - Chân trời sáng tạo

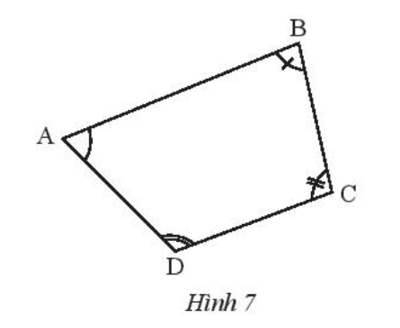
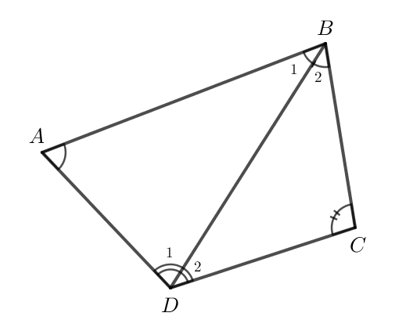
Bài 3 trang 47 Toán 7 Tập 2: Hãy chia tứ giác ABCD trong Hình 7 thành hai tam giác để tính tổng số đo của bốn góc $\hat{A},\hat{B},\hat{C},\hat{D}$.

Lời giải:

Nối BD.

Xét tam giác ABD: $\hat{A}+{\hat{B}}_1+{\hat{D}}_1=180°$.

Xét tam giác BCD: ${\hat{B}}_2+\hat{C}+{\hat{D}}_2=180°$.

Do đó $\hat{A}+{\hat{B}}_1+{\hat{D}}_1+{\hat{B}}_2+\hat{C}+{\hat{D}}_2$= 180^o + 180^o = 360^o.

Suy ra $\hat{A}+\left({\hat{B}}_1+{\hat{B}}_2\right)+\hat{C}+\left({\hat{D}}_1+{\hat{D}}_2\right)$= 360^o.

Hay $\hat{A}+\hat{B}+\hat{C}+\hat{D}$= 360^o.

Vậy tổng số đo bốn góc $\hat{A},\hat{B},\hat{C},\hat{D}$trong hình trên bằng 360^o.

Lời giải bài tập Toán 7 Bài 1: Góc và cạnh của một tam giác hay, chi tiết khác:

Bài 4 trang 47 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 1: Góc và cạnh của một tam giác - Chân trời sáng tạo

Bài 4 trang 47 Toán 7 Tập 2: Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác?

a) 4 cm, 5 cm, 7 cm;

b) 2 cm, 4 cm, 6 cm;

c) 3 cm, 4 cm, 8 cm.

Lời giải:

a) Ta thấy 7 < 4 + 5 nên bộ ba độ dài 4 cm, 5 cm, 7 cm có thể là độ dài ba cạnh của một tam giác.

b) Ta thấy 6 = 2 + 4 nên bộ ba độ dài 2 cm, 4 cm, 6 cm không thể là độ dài ba cạnh của một tam giác.

c) Ta thấy 8 > 3 + 4 nên bộ ba độ dài 3 cm, 4 cm, 8 cm không thể là độ dài ba cạnh của một tam giác.

Lời giải bài tập Toán 7 Bài 1: Góc và cạnh của một tam giác hay, chi tiết khác:

Bài 5 trang 47 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 1: Góc và cạnh của một tam giác - Chân trời sáng tạo

Bài 5 trang 47 Toán 7 Tập 2: Cho tam giác ABC có BC = 1 cm, AB = 4 cm. Tính độ dài cạnh AC (theo đơn vị cm), biết rằng độ dài này là một số nguyên.

Lời giải:

Trong tam giác ABC:

AB - BC < AC < AB + BC hay 4 - 1 < AC < 4 + 1 hay 3 < AC < 5.

Mà độ dài cạnh AC là một số nguyên nên AC = 4 cm.

Vậy AC = 4 cm.

Lời giải bài tập Toán 7 Bài 1: Góc và cạnh của một tam giác hay, chi tiết khác:

Bài 6 trang 47 Toán 7 Tập 2 Chân trời sáng tạo

Giải Toán 7 Bài 1: Góc và cạnh của một tam giác - Chân trời sáng tạo

Bài 6 trang 47 Toán 7 Tập 2: Trong một trường học, người ta đánh dấu ba khu vực A, B, C là ba đỉnh của một tam giác, biết các khoảng cách AC = 15 m, AB = 45 m.

a) Nếu đặt ở khu vực C một thiết bị phát wifi có bán kính hoạt động 30 m thì tại khu vực B có nhận được tín hiệu không? Vì sao?

b) Cũng câu hỏi như trên với thiết bị phát wifi có bán kính hoạt động 60 m.

Lời giải:

a) Trong tam giác ABC:

AB - AC < BC hay 45 - 15 < BC hay 30 < BC.

Do đó nếu đặt ở khu vực C một thiết bị phát wifi có bán kính hoạt động 30 m thì tại khu vực B không nhận được tín hiệu.

b) Trong tam giác ABC:

BC < AB + AC hay BC < 45 + 15 hay BC < 60.

Do đó nếu đặt ở khu vực C một thiết bị phát wifi có bán kính hoạt động 60 m thì tại khu vực B nhận được tín hiệu.

Lời giải bài tập Toán 7 Bài 1: Góc và cạnh của một tam giác hay, chi tiết khác:

Sách bài tập Toán 7 Bài 1: Góc và cạnh của một tam giác - Chân trời sáng tạo

Với giải sách bài tập Toán 7 Bài 1: Góc và cạnh của một tam giác sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Bài 1.

Giải SBT Toán 7 Bài 1: Góc và cạnh của một tam giác - Chân trời sáng tạo

Giải SBT Toán 7 trang 41 Tập 2

Vở thực hành Toán 7 Bài 1: Góc và cạnh của một tam giác - Chân trời sáng tạo

Với giải vở thực hành Toán lớp 7 Bài 1: Góc và cạnh của một tam giác sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập về nhà trong VTH Toán 7 Bài 1.

Giải vở thực hành Toán 7 Bài 1: Góc và cạnh của một tam giác - Chân trời sáng tạo

B. Câu hỏi trắc nghiệm

Chọn phương án đúng trong mỗi câu sau:

Giải VTH Toán 7 trang 32 Tập 2

Góc và cạnh của một tam giác (Lý thuyết Toán lớp 7) - Chân trời sáng tạo

Với tóm tắt lý thuyết Toán 7 Bài 1: Góc và cạnh của một tam giác hay nhất, chi tiết sách Chân trời sáng tạo sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Góc và cạnh của một tam giác (Lý thuyết Toán lớp 7) - Chân trời sáng tạo

Lý thuyết Góc và cạnh của một tam giác

1. Tổng số đo ba góc của một tam giác

* Định lí: Tổng số đo của ba góc của một tam giác bằng 180°.

Ví dụ: Cho tam giác ABC. Khi đó ta có: $\overbrace{A}+\overbrace{B}+\overbrace{C}={180}^o$

* Chú ý:

- Tam giác có 3 góc nhọn được gọi là tam giác nhọn.

Ví dụ: Cho tam giác ABC có $\overbrace{A}={45}^o;\overbrace{B}={60}^o;\overbrace{C}={75}^o$ là các góc nhọn nên tam giác ABC là tam giác nhọn.

- Tam giác có một góc vuông được gọi là tam giác vuông, cạnh đối diện góc vuông gọi là cạnh huyền, hai cạnh còn lại gọi là hai cạnh góc vuông.

Ví dụ: Tam giác DEF có $\overbrace{D}={90}^o$ suy ra tam giác DEF là tam giác vuông. Trong đó cạnh EF là cạnh huyền; DE và DF là hai cạnh góc vuông.

- Tam giác có một góc tù được gọi là tam giác tù.

Ví dụ: Tam giác IHK có $\overbrace{H}={120}^o$là một góc tù nên suy ra tam giác IHK là một tam giác tù.

* Nhận xét: Trong một tam giác vuông, tổng hai góc nhọn bằng 90°

Ví dụ: Cho tam giác ABC vuông tại A khi đó ta có: $\overbrace{B}+\overbrace{C}={90}^o$

2. Quan hệ giữa ba cạnh của một tam giác

* Định lí: Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn hai cạnh còn lại.

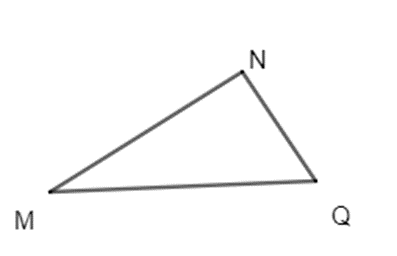
Ví dụ: Cho tam giác MNQ

Ta luôn có:

MN + MQ > NQ;

MN + NQ > MQ;

MQ + NQ > MN.

* Nhận xét: Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng độ dài của hai cạnh còn lại.

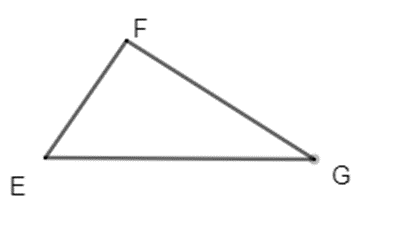
Ví dụ: Cho tam giác EFG

Với cạnh EF ta có:

EG – FG < EF < EG + FG hay FG – EG < EF < EG + FG.

* Lưu ý: Khi xét độ dài ba đoạn thẳng có thỏa mãn các bất đẳng thức tam giác hay không, ta chỉ cần so sánh độ dài lớn nhát với tổng của hai độ dài còn lại, hoặc so sánh độ dài nhỏ nhất với hiệu của hai độ dài còn lại.

Ví dụ:

a) Cho bộ ba độ dài đoạn thẳng là: 3 cm; 4 cm ; 5 cm.

Ta thấy 3 + 4 = 7 > 5.

Suy ra bộ ba độ dài đoạn thẳng này là độ dài ba cạnh của một tam giác.

b) Cho bộ ba độ dài đoạn thẳng là: 3 cm; 4 cm ; 10 cm

Ta thấy 3 + 4 = 7 < 10.

Suy ra bộ ba độ dài đoạn thẳng này không thể là độ dài ba cạnh của một tam giác.

Bài tập Góc và cạnh của một tam giác

Bài 1: Tìm số đo các góc chưa biết của các tam giác sau:

a)

b)

Hướng dẫn giải:

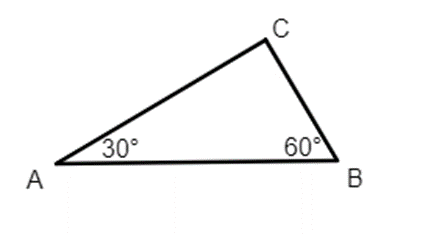
a) Xét tam giác ABC, theo định lí tổng các góc trong tam giác ta có:

$\overbrace{A}+\overbrace{B}+\overbrace{C}={180}^o$

Suy ra $\overbrace{C}={180}^o-\overbrace{A}-\overbrace{B}$

= 180° − 30° − 60° = 90°.

Vậy $\overbrace{C}={90}^o$.

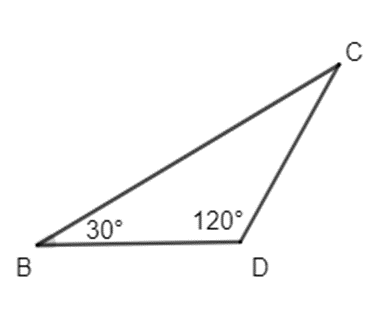
b) Xét tam giác BCD, theo định lí tổng các góc trong tam giác ta có:

$\overbrace{B}+\overbrace{C}+\overbrace{D}={180}^o$

Suy ra $\overbrace{C}={180}^o-\overbrace{B}-\overbrace{D}$

= 180° − 30° − 120° = 30°

Vậy $\overbrace{C}={30}^o$.

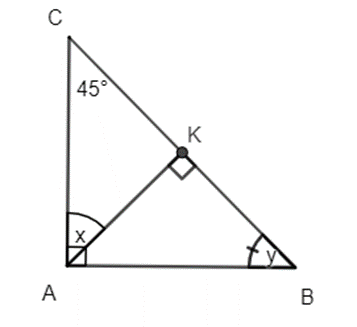
Bài 2: Tính tổng số đo của các góc x và y trong hình sau:

Hướng dẫn giải:

Xét tam giác ABC, theo định lí tổng các góc trong tam giác ta có:

$\overbrace{A}+\overbrace{B}+\overbrace{C}={180}^o$

Suy ra $\overbrace{B}={180}^o-\overbrace{A}-\overbrace{C}$

= 180° − 90° − 45° = 45° = y

Tương tự xét tam giác AKC, theo định lí tổng các góc trong tam giác ta có:

$\overbrace{A}+\overbrace{K}+\overbrace{C}={180}^o$

Suy ra $\overbrace{A}={180}^o-\overbrace{C}-\overbrace{K}$

= 180° − 90° − 45° = 45° = x

Vậy x + y = 45° + 45° = 90°.

Bài 3: Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác?

a) 6 cm, 8 cm, 10 cm;

b) 3 cm, 2 cm, 6 cm;

c) 3 cm, 2 cm, 5 cm.

Hướng dẫn giải:

a) Ta thấy: 10 < 6 + 8 = 12

Suy ra bộ ba độ dài đoạn thẳng 6 cm, 8 cm, 10 cm có thể là bộ ba độ dài cạnh của một tam giác.

b) Ta thấy: 6 > 2 + 3 = 5

Suy ra bộ ba độ dài đoạn thẳng 3 cm, 2 cm, 6 cm không thể là bộ ba độ dài cạnh của một tam giác.

c) Ta thấy: 5 = 3 + 2

Suy ra bộ ba độ dài đoạn thẳng 3 cm, 2 cm, 5 cm không thể là bộ ba độ dài cạnh của một tam giác.

Vậy trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba 6 cm, 8 cm, 10 cm có thể là độ dài ba cạnh của một tam giác.

Bài 4: Cho tam giác HIK có HK = 4 cm, HI = 1 cm. Tìm độ dài của cạnh IK, biết rằng độ dài này là một số nguyên.

Hướng dẫn giải:

Dựa vào quan hệ của các cạnh trong một tam giác ta có:

HK – HI < IK < HK + HI

Suy ra 4 – 1 < IK < 4 + 1

3 < IK < 5

Vì độ dài IK là một sô nguyên nên suy ra IK = 4 cm.

Vậy độ dài của IK = 4 cm.

Học tốt Góc và cạnh của một tam giác

Các bài học để học tốt Góc và cạnh của một tam giác Toán lớp 7 hay khác:

15 Bài tập Góc và cạnh của một tam giác (có đáp án) - Chân trời sáng tạo Trắc nghiệm Toán 7

Với 15 bài tập trắc nghiệm Góc và cạnh của một tam giác Toán lớp 7 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Chân trời sáng tạo sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 7.

15 Bài tập Góc và cạnh của một tam giác (có đáp án) - Chân trời sáng tạo Trắc nghiệm Toán 7

Xem thử

Chỉ từ 150k mua trọn bộ trắc nghiệm Toán 7 Chân trời sáng tạo (cả năm) có lời giải chi tiết, bản word trình bày đẹp mắt, dễ dàng chỉnh sửa: