Tiên đề Euclid. Tính chất của hai đường thẳng song song (Lý thuyết Toán lớp 7) - Kết nối tri thức
Với tóm tắt lý thuyết Toán 7 Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song sách Kết nối tri thức hay nhất, chi tiết
sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.
Tiên đề Euclid. Tính chất của hai đường thẳng song song (Lý thuyết Toán lớp 7) - Kết nối tri thức
Lý thuyết Tiên đề Euclid. Tính chất của hai đường thẳng song song
1. Tiên đề Euclid về đường thẳng song song
• Tiên đề Euclid: Qua một điểm ở ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.
Ví dụ:
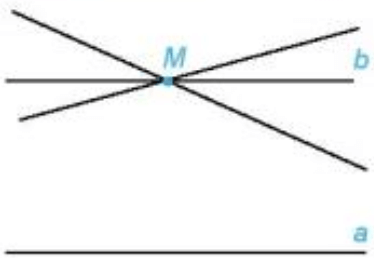
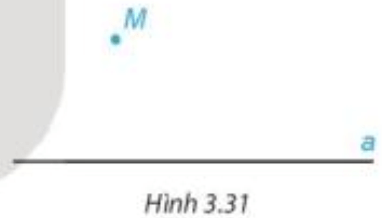
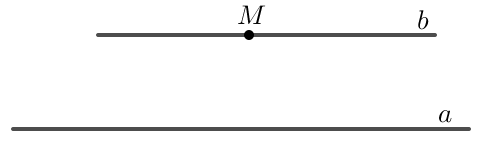
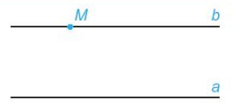
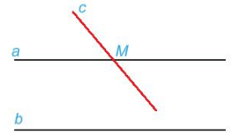
+ Cho điểm M nằm ngoài đường thẳng a thì b đi qua M và song song với a là duy nhất.
Chú ý:
• Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cũng cắt đường thẳng còn lại.
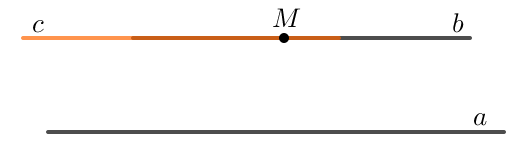
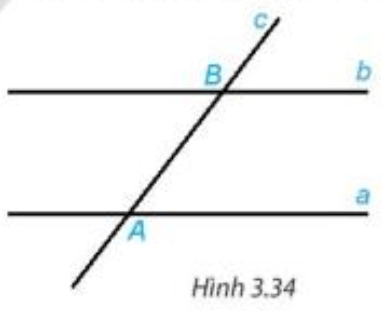
Ví dụ: Cho a và b là hai đường thẳng song song với nhau. Nếu đường thẳng c cắt đường thẳng a thì cũng cắt đường thẳng b.
2. Tính chất của hai đường thẳng song song
• Nếu một đường thẳng cắt hai đường thẳng song song thì:
+ Hai góc so le trong bằng nhau;
+ Hai góc đồng vị bằng nhau.
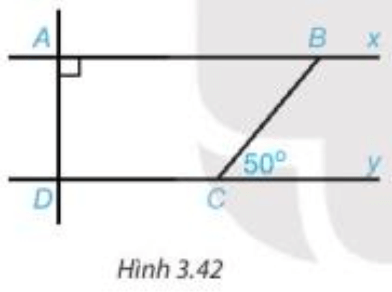
Ví dụ: Cho và . Tính và
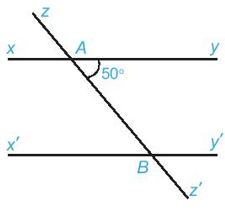
Vì (hai góc so le trong). Do đó
Vì (hai góc đồng vị). Do đó
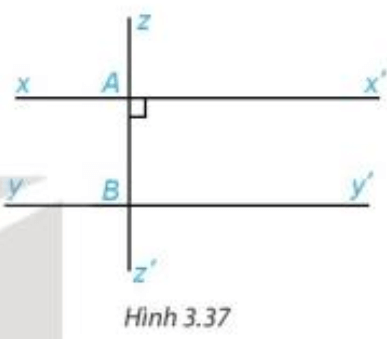
• Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
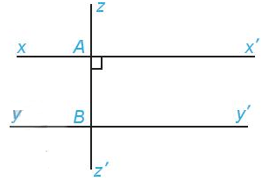
Ví dụ: Cho và thì
• Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.
Ví dụ: Cho và thì

Bài tập Tiên đề Euclid. Tính chất của hai đường thẳng song song
Bài 1. Cho tam giác ABC. Vẽ đường thẳng m đi qua A và song song với BC. Vẽ đường thẳng n đi qua B và song song với AC. Có thể vẽ được bao nhiêu đường thẳng m, bao nhiêu đường thẳng n? Vì sao?
Hướng dẫn giải
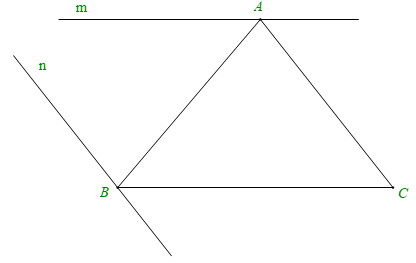
Vì theo tiên đề Euclid, qua điểm A ở ngoài BC, chỉ có một đường thẳng song song với BC. Nên chỉ vẽ được một đường thẳng m duy nhất.
Vì theo tiên đề Euclid, qua điểm B ở ngoài AC, chỉ có một đường thẳng song song với AC. Nên chỉ vẽ được một đường thẳng n duy nhất.
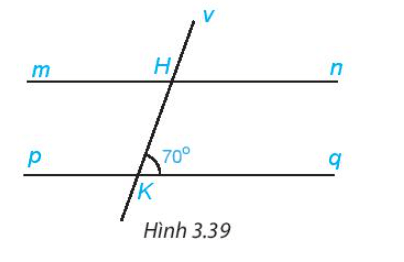
Bài 2. Cho hình vẽ, biết và .
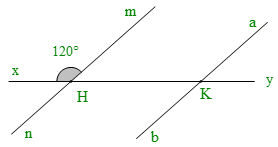
Tính các góc còn lại trong hình vẽ.
Hướng dẫn giải
Ta có: (hai góc đối đỉnh)
Ta có: (hai góc kề bù)
Thay số:
Có: (hai góc đối đỉnh)
Vì nên:
(hai góc so le trong)
(hai góc đồng vị)
(hai góc đồng vị)
(hai góc đồng vị)
Vậy ; <; ; ; ; ; .
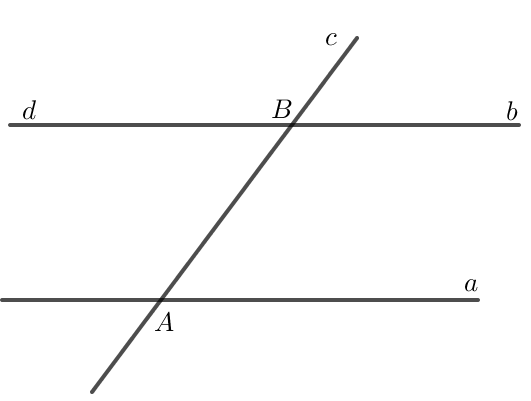
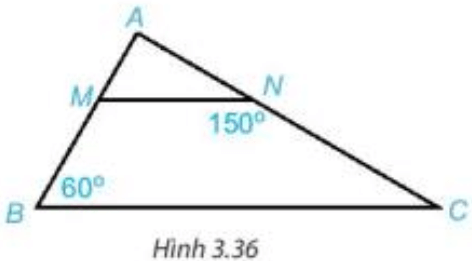
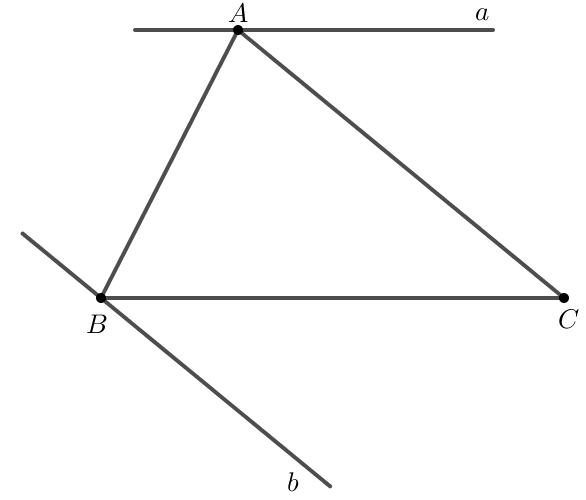
Bài 3. Cho hình dưới đây. Giải thích tại sao:
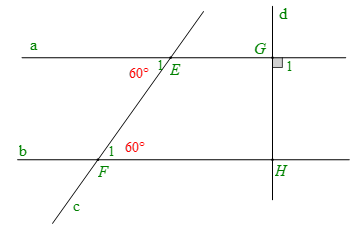
a) ;
b) .
Hướng dẫn giải
a) Ta có:
Mà hai góc ở vị trí so le trong.
Do đó (dấu hiệu nhận biết hai đường thẳng song song).
b) Ta có: nên
Mà (theo câu a)
Do đó (tính chất hai đường thẳng song song).
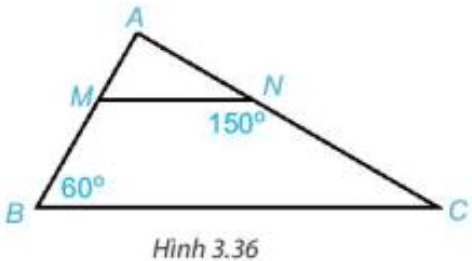
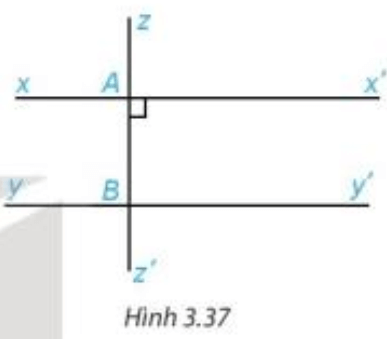
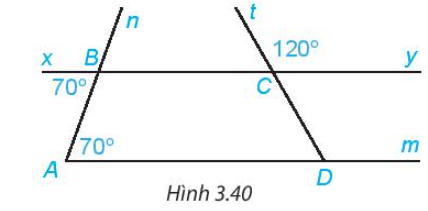
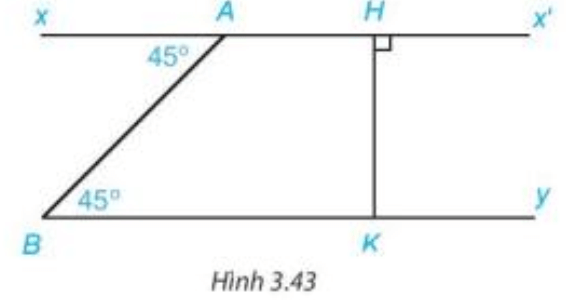
Bài 4. Cho hình dưới đây. Giải thích tại sao:
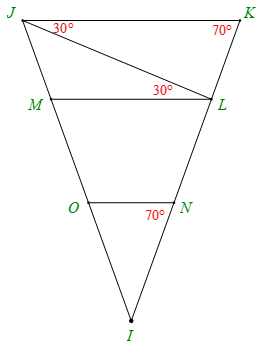
a) ;
b) ;
c)
Hướng dẫn giải
a) Ta có:
Mà hai góc ở vị trí so le trong.
Do đó (dấu hiệu nhận biết hai đường thẳng song song).
b) Ta có:
Mà hai góc ở vị trí đồng vị.
Do đó (dấu hiệu nhận biết hai đường thẳng song song).
c) Ta có: (theo câu a) và (theo câu b)
Do đó (tính chất hai đường thẳng song song).
Học tốt Tiên đề Euclid. Tính chất của hai đường thẳng song song
Các bài học để học tốt Tiên đề Euclid. Tính chất của hai đường thẳng song song Toán lớp 7 hay khác: