Đại lượng tỉ lệ nghịch (Lý thuyết Toán lớp 7) - Kết nối tri thức
Với tóm tắt lý thuyết Toán 7 Bài 23: Đại lượng tỉ lệ nghịch sách Kết nối tri thức hay nhất, chi tiết
sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.
Đại lượng tỉ lệ nghịch (Lý thuyết Toán lớp 7) - Kết nối tri thức
Lý thuyết Đại lượng tỉ lệ nghịch
1. Đại lượng tỉ lệ nghịch
• Nếu đại lượng y liên hệ với đại lượng x theo công thức (a là một hằng số khác 0) thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a.
Chú ý:
Nếu y tỉ lệ nghịch với x theo hệ số tỉ lệ a thì x cũng tỉ lệ nghịch với y theo hệ số tỉ lệ a và ta nói hai đại lượng x và y tỉ lệ nghịch với nhau.
Ví dụ: Nếu thì y tỉ lệ nghịch với x theo hệ số 3, hay x tỉ lệ nghịch với y theo hệ số 3.
Nhận xét:
Nếu hai đại lượng y và x tỉ lệ nghịch với nhau thì:
• Tích hai giá trị tương ứng của chúng luôn không đổi (và bằng hệ số tỉ lệ):
hay
• Tỉ số hai giá trị bất kì của đại lượng này bằng nghịch đảo của tỉ số hai giá trị tương ứng của đại lượng kia:
Ví dụ: Cho biết x và y là hai đại lượng tỉ lệ nghịch. Điền số thích hợp vào ô trống trong bảng sau:
x |
0,5 |
-1,2 |
|
|
4 |
6 |
y |
|
|
3 |
-2 |
1,5 |
|
Hướng dẫn giải:
Gọi hệ số tỉ lệ của x và y là a, nghĩa là hay x . y = a.
Ta có x = 4 thì y = 1,5 nên suy ra a = x.y = 4 . 1,5 = 6.
Vậy x . y = 6.
Khi x = 0,5 thì y = 6 : 0,5 = 12
Khi x = -1,2 thì y = 6 : (-1,2) = -5
Khi y = 3 thì x = 6 : 3 = 2
Khi y = -2 thì x = 6 : (-2) = -3
Khi x = 6 thì y = 6 : 6 = 1
Vậy ta có bảng sau:
x |
0,5 |
-1,2 |
2 |
-3 |
4 |
6 |
y |
12 |
-5 |
3 |
-2 |
1,5 |
1 |
2. Một số bài toán về đại lượng tỉ lệ nghịch
Để giải toán về đại lượng tỉ lệ nghịch, ta cần nhận biết được hai đại lượng tỉ lệ nghịch trong bài toán. Từ đó ta có thể lập các tỉ số bằng nhau và dựa vào tính chất của dãy tỉ số bằng nhau để tìm các yếu tố chưa biết.
Ví dụ:
Cho biết 35 công nhân xây một ngôi nhà hết 168 ngày. Hỏi 28 công nhân xây một ngôi nhà trong bao nhiêu ngày? (Giả sử năng suất làm việc của mỗi công nhân là như nhau)
Hướng dẫn giải:
Vì năng suất làm việc của mỗi người là như nhau nên số công nhân và số ngày xây xong ngôi nhà là hai đại lượng tỉ lệ nghịch.
Gọi số công nhân là y (công nhân); số ngày xây xong ngôi nhà là x (ngày). (y ; x > 0)
Ta có x . y = a
Khi y = 35 thì x = 168 nên ta có a = 35 . 168 = 5880.
Do đó x . y = 5880.
Vậy khi y = 28 thì x = 5880 : 28 =210.
Vậy 28 công nhân xây ngôi nhà đó hết 210 ngày.
Bài tập Đại lượng tỉ lệ nghịch
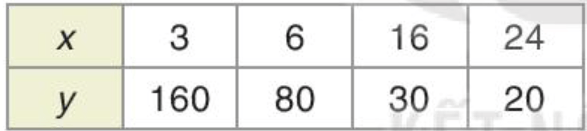
Bài 1. Hai đại lượng x và y có tỉ lệ nghịch với nhau hay không, nếu:
a)
x |
1 |
2 |
4 |
5 |
8 |
y |
120 |
60 |
30 |
24 |
15 |
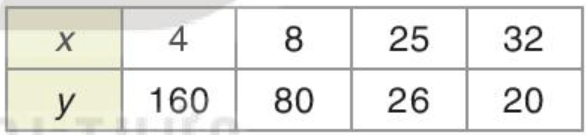
b)
x |
2 |
3 |
4 |
5 |
6 |
y |
30 |
20 |
15 |
12,5 |
10 |
Hướng dẫn giải:
a) Ta có 1 . 20 = 2 . 60 = 4 . 30 = 5 . 24 = 8 . 15 = 120.
Nên x và y là hai đại lượng tỉ lệ nghịch với nhau.
b) Vì 5 . 12,5 ≠ 6 . 10 nên x và y không tỉ lệ nghịch với nhau.
Bài 2. Cho biết hai đại lượng x và y tỉ lệ nghịch với nhau. Điền số thích hợp vào ô trống:
Hướng dẫn giải:
Nhìn vào bảng ta thấy khi x = 10 thì y = 1,6. Do đó hệ số tỉ lệ a = 10 . 1,6 = 16.
Vậy x . y = 16.
Do đó:
Khi x = 1 thì y = 16 : 1 = 16
Khi y = 8 thì x = 16 : 8 = 2
Khi y = -4 thì x = 16: (-4) = -4
Khi y =
Khi x = -8 thì y = 16 : (-8) = -2.
Từ đó ta có bảng sau :
x |
1 |
2 |
-4 |
6 |
-8 |
10 |
y |
16 |
8 |
-4 |
|
-2 |
1,6 |
Bài 3. Cho biết 3 người làm cỏ một cánh đồng hết 6 giờ. Hỏi 12 người (có cùng năng suất) làm cỏ cánh đồng đó hết bao nhiêu thời gian?
Hướng dẫn giải:
Với cùng một cánh đồng nên số người làm cỏ hết cánh đồng đó và số giờ là hai đại lượng tỉ lệ nghịch.
Hệ số tỉ lệ bằng 3 . 6 = 18.
Gọi số giờ để 12 người làm cỏ hết cánh đồng là x (giờ) (x > 0)
Theo tính chất của đại lượng tỉ lệ nghịch ta có x . 12 = 18 suy ra x = 18 : 12 = 1,5.
Vậy 12 người làm cỏ cánh đồng hết 1,5 giờ (1 giờ 30 phút).
Bài 4. Với cùng số tiền để mua 51 mét vải loại I có thể mua được bao nhiêu mét vải loại II, biết rằng giá tiền 1 mét vải loại II chỉ bằng 85% giá tiền vải loại I?
Hướng dẫn giải:
Gọi giá tiền 1 mét vải loại I là x1; giá tiền 1m vải loại II là x2.
Với cùng một số tiền, số mét vải loại I và loại II mua được tương ứng là y1; y2 (m).
Theo đề bài có: y1 = 51; x2 = 85%.x1 = 0,85.x1.
Với cùng một số tiền thì giá tiền 1 mét vải và số vải mua được là hai đại lượng tỉ lệ nghịch nên ta có:
Mà (m)
Vậy với cùng số tiền đó ta có thể mua được 60m vải loại II.
Học tốt Đại lượng tỉ lệ nghịch
Các bài học để học tốt Đại lượng tỉ lệ nghịch Toán lớp 7 hay khác: