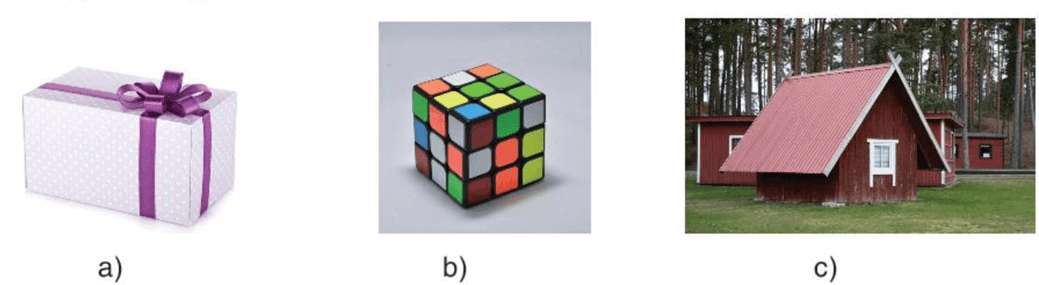Với giải bài tập Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương sách Kết nối tri thức hay nhất, chi tiết giúp học sinh lớp 7 dễ dàng làm bài tập Toán Hình 7 Bài 36.

Giải Toán 7 Kết nối tri thức Bài 36: Hình hộp chữ nhật và hình lập phương

1. Hình hộp chữ nhật, hình lập phương

Giải Toán 7 trang 86 Tập 2

HĐ1 trang 86 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương

HĐ1 trang 86 Toán 7 Tập 2: Hình nào dưới đây là đồ vật hoặc kiến trúc có dạng hình hộp chữ nhật, có dạng hình lập phương?

Em hãy tìm thêm một số hình ảnh có dạng hình hộp chữ nhật, hình lập phương trong thực tế.

Lời giải:

Hộp quà ở ý a có dạng hình hộp chữ nhật.

Khối rubik ở ý b có dạng hình lập phương.

Một số hình có dạng hình hộp chữ nhật: hộp bút, quyển sách, căn phòng …

Hình có dạng hình lập phương: con xúc xắc …

Lời giải bài tập Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương hay, chi tiết khác:

HĐ2 trang 86 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương

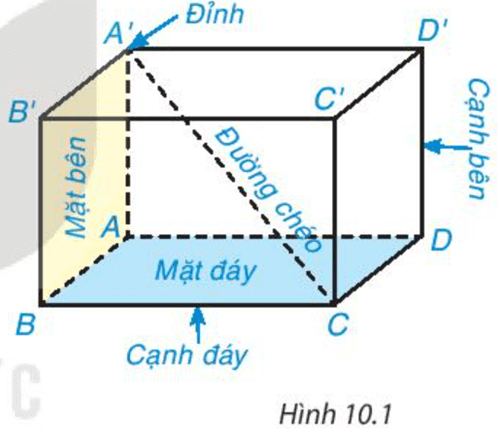
HĐ2 trang 86 Toán 7 Tập 2: Quan sát Hình 10.1.

a) Nêu tên các đỉnh, cạnh, đường chéo của hình hộp chữ nhật ABCD.A’B’C’D’.

Hình hộp chữ nhật có bao nhiêu đỉnh? Có bao nhiêu cạnh? Có bao nhiêu đường chéo?

b) Gọi tên các mặt bên, mặt đáy của hình hộp chữ nhật ABCD.A’B’C’D’.

Lời giải:

a) Các đỉnh của hình hộp chữ nhật ABCD.A’B’C’D’ là: A, B, C, D, A’, B’, C’, D’.

Các cạnh của hình hộp chữ nhật ABCD.A’B’C’D’ là: AB, BC, CD, DA, A’B’, B’C’, C’D’, D’A’, AA’, BB’, CC’, DD’.

Các đường chéo của hình hộp chữ nhật ABCD.A’B’C’D’ là: A’C, B’D, C’A. D’B.

Hình hộp chữ nhật có 8 đỉnh, 12 cạnh, 4 đường chéo.

b) Các mặt bên của hình hộp chữ nhật ABCD.A’B’C’D’ là: ABB’A’, AA’D’D, CDD’C’, BCC’B’.

Các mặt đáy của hình hộp chữ nhật ABCD.A’B’C’D’ là: ABCD, A’B’C’D’.

Lời giải bài tập Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương hay, chi tiết khác:

HĐ3 trang 86 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương

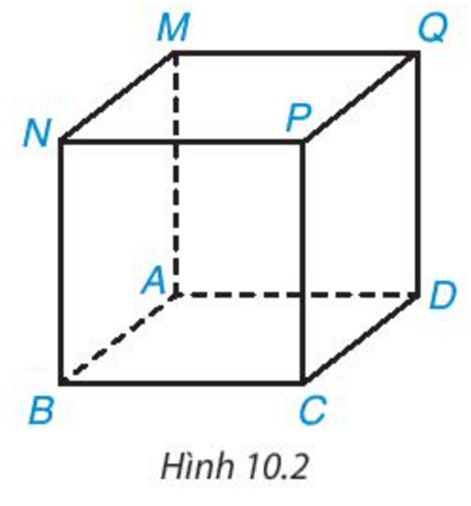
HĐ3 trang 86 Toán 7 Tập 2: Quan sát Hình 10.2 và gọi tên đỉnh, cạnh, đường chéo, mặt đáy, mặt bên của hình lập phương MNPQ.ABCD.

Lời giải:

Các đỉnh của hình lập phương MNPQ.ABCD là: M, N, P, Q, A, B, C, D.

Các cạnh của hình lập phương MNPQ.ABCD là: MN, NP, PQ, QM, AB, BC, CD, DA, MA, NB, PC, QD.

Các đường chéo của hình lập phương MNPQ.ABCD là: MC, ND, PA, QB.

Các mặt đáy của hình lập phương MNPQ.ABCD là: MNPQ, ABCD.

Các mặt bên của hình lập phương MNPQ.ABCD là: MNBA, NBCP, PCDQ, MADQ.

Lời giải bài tập Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương hay, chi tiết khác:

Thực hành trang 87 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương

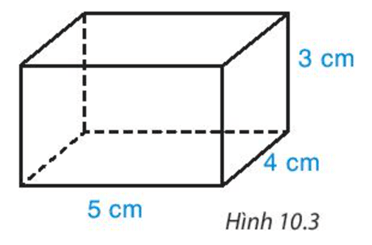
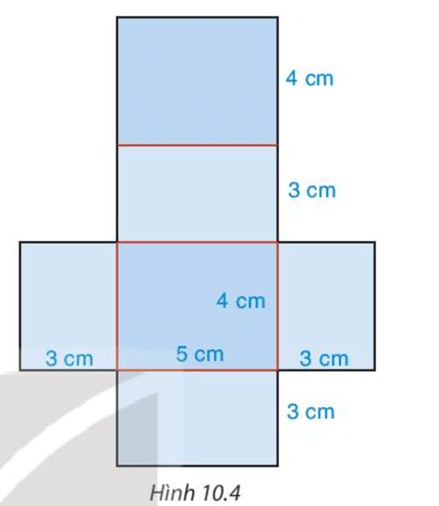
Thực hành trang 87 Toán 7 Tập 2: Sử dụng bìa cứng, cắt và gấp một chiếc hộp có dạng hình hộp chữ nhật với kích thước như Hình 10.3 theo hướng dẫn sau:

Bước 1. Vẽ hình triển khai của hình hộp chữ nhật theo kích thước đã cho như Hình 10.4.

Bước 2. Cắt theo viền.

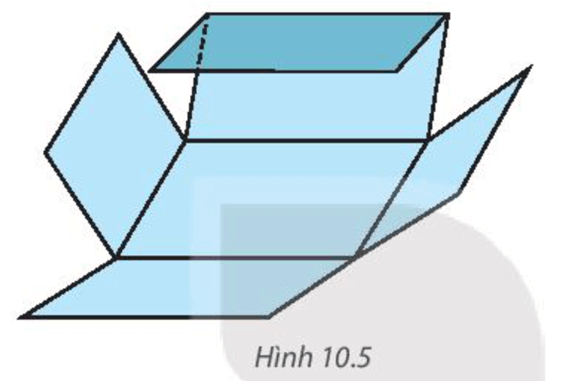
Bước 3. Gấp theo đường màu cam để được hình hộp chữ nhật (H.10.5).

Lời giải:

Học sinh tự thực hiện theo hướng dẫn.

Lời giải bài tập Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương hay, chi tiết khác:

Vận dụng 1 trang 87 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương

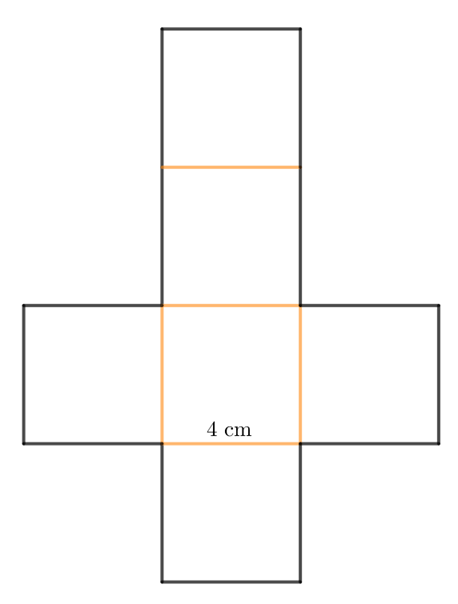
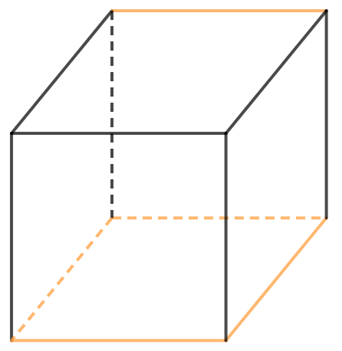
Vận dụng 1 trang 87 Toán 7 Tập 2: Hãy cắt và gấp hình lập phương có cạnh 4 cm.

Lời giải:

Thực hiện theo các bước như sau:

Bước 1. Vẽ hình triển khai của hình lập phương với độ dài cạnh bằng 4 cm.

Bước 2. Cắt theo viền.

Bước 3. Gấp theo đường màu cam để được hình lập phương.

Lời giải bài tập Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương hay, chi tiết khác:

HĐ4 trang 87 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương

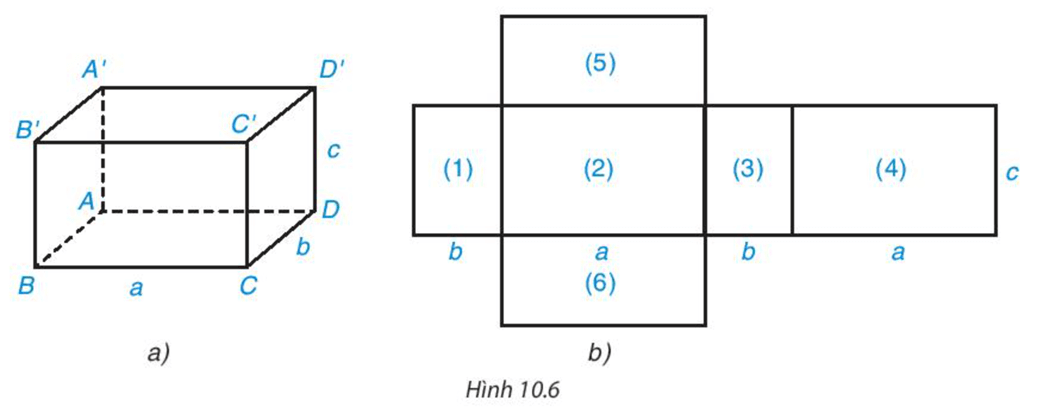
HĐ4 trang 87 Toán 7 Tập 2: Quan sát hình hộp chữ nhật (H.10.6a) và hình triển khai của nó (H.10.6b). Hãy chỉ ra sự tương ứng giữa các mặt của hình hộp chữ nhật với các hình chữ nhật ở hình khai triển. Hình chữ nhật nào ở hình khai triển là các mặt bên, là các mặt đáy?

Lời giải:

Vì hình chữ nhật (1) có cạnh là b và c nên nó có thể là mặt AA’B’B hoặc CC’D’D. Ta có thể chọn mặt đó là ABB’A’.

Hình chữ nhật (2) có cạnh là a và c nên nó có thể là mặt BB’C’C hoặc mặt AA’D’D. Ta có thể chọn mặt đó là AA’D’D.

Hình chữ nhật (3) có cạnh là b và c nên nó là mặt CC’D’D (do AA’B’B đã chọn là hình (1))

Hình chữ nhật (4) có cạnh là a và c nên nó là mặt BB’C’C (do AA’D’D đã được chọn là hình (2)).

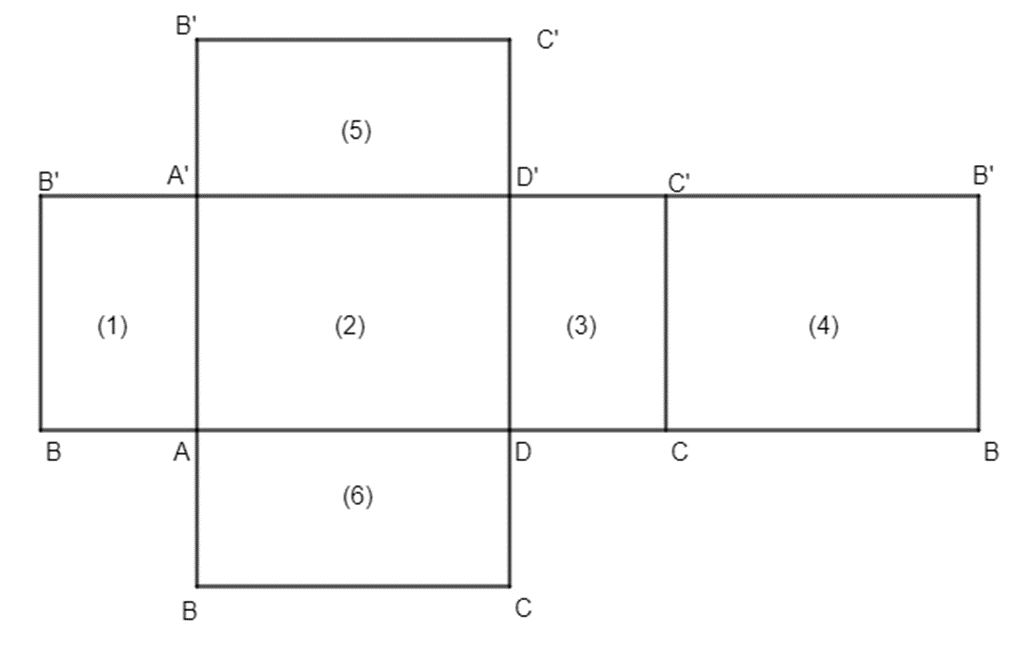
Hình chữ nhật (5) và hình chữ nhật (6) là hai mặt còn lại ABCD và A’B’C’D. Vì hai hình chữ nhật này bằng nhau nên ta chọn hình chữ nhật (5) là A’B’C’D’ và hình chữ nhật (6) là ABCD.

Khi đó, ta có hình vẽ:

Vậy khai triển của các mặt bên là hình chữ nhật (1); (2); (3); (4).

Khi triển của các mặt đáy là (5); (6).

Lời giải bài tập Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương hay, chi tiết khác:

HĐ5 trang 87 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương

HĐ5 trang 87 Toán 7 Tập 2: Tính tổng diện tích các hình chữ nhật (1), (2), (3), (4). So sánh kết quả vừa tìm với tích của chu vi đáy và chiều cao của hình hộp chữ nhật.

Lời giải:

Diện tích hình (1) là bc, diện tích hình (2) là ac, diện tích hình (3) là bc, diện tích hình (4) là ac.

Khi đó tổng diện tích các hình (1), (2), (3), (4) là:

ac + bc + bc + ac = 2(ac + bc) = 2(a + b)c.

Chu vi đáy của hình hộp chữ nhật là 2(a + b).

Khi đó tích của chu vi đáy và chiều cao của hình hộp chữ nhật là 2(a + b)c.

Vậy hai kết quả vừa tìm được bằng nhau.

Lời giải bài tập Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương hay, chi tiết khác:

Luyện tập 1 trang 88 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương

Luyện tập 1 trang 88 Toán 7 Tập 2: Bác Tú thuê thợ sơn xung quanh bốn mặt ngoài của thành bể nước có dạng hình hộp chữ nhật có chiều dài 3 m, chiều rộng 2 m, chiều cao 1,5 m với giá 20 000 đồng/m². Hỏi bác Tú phải trả chi phí là bao nhiêu?

Lời giải:

Diện tích xung quanh của bể nước là: 2.(3 + 2).1,5 = 15 (m²).

Bác Tú phải trả số tiền là: 20 000 . 15 = 300 000 (đồng).

Vậy bác Tú phải trả 300 000 đồng.

Lời giải bài tập Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương hay, chi tiết khác:

Luyện tập 2 trang 90 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương

Luyện tập 2 trang 90 Toán 7 Tập 2: Một hình lập phương có cạnh bằng a cm, diện tích xung quanh bằng 100 cm². Hỏi thể tích của hình lập phương đó bằng bao nhiêu?

Lời giải:

Do hình lập phương có cạnh bằng a cm nên diện tích xung quanh của hình lập phương đó là 4a² = 100

hay a² = 25 do đó a = 5 cm (do a là độ dài cạnh hình lập phương nên a > 0).

Khi đó thể tích của hình lập phương đó bằng 5³ = 125 (cm³).

Vậy thể tích của hình lập phương bằng 125 cm³.

Lời giải bài tập Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương hay, chi tiết khác:

Vận dụng 2 trang 90 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương

Vận dụng 2 trang 90 Toán 7 Tập 2: Một chiếc thùng giữ nhiệt (H.10.10) có lòng trong có dạng một hình hộp chữ nhật với chiều dài 50 cm, chiều rộng 30 cm, chiều cao 30 cm. Tính dung tích của thùng giữ nhiệt đó.

Lời giải:

Dung tích của chiếc thùng là: 50 . 30 . 30 = 45 000 (cm³).

Đổi 45 000 cm³ = 45 dm³ = 45 l.

Vậy dung tích của thùng giữ nhiệt là 45 l.

Lời giải bài tập Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương hay, chi tiết khác:

Bài 10.1 trang 90 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương

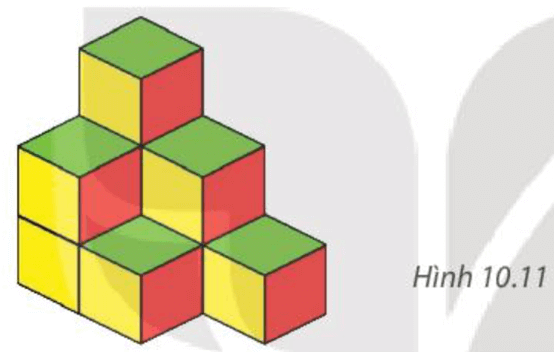
Bài 10.1 trang 90 Toán 7 Tập 2: Có bao nhiêu hình lập phương nhỏ trong Hình 10.11?

Lời giải:

Xét hàng đầu tiên, ta có 1 hình lập phương.

Xét hàng thứ hai, ta có 3 hình lập phương.

Xét hàng thứ ba, ta có 5 hình lập phương.

Vậy có tất cả 1 + 3 + 5 = 9 hình lập phương.

Lời giải bài tập Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương hay, chi tiết khác:

Bài 10.2 trang 90 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương

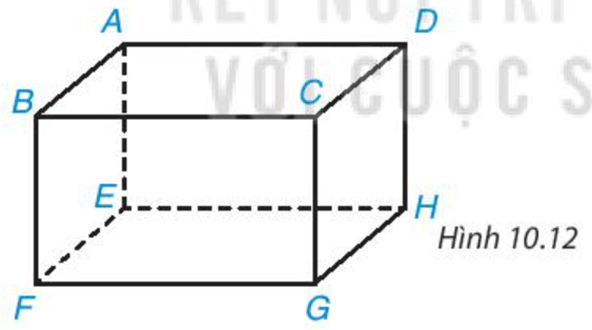
Bài 10.2 trang 90 Toán 7 Tập 2: Gọi tên các đỉnh, cạnh, đường chéo, mặt của hình hộp chữ nhật trong Hình 10.12.

Lời giải:

Các đỉnh của hình hộp chữ nhật là: A, B, C, D, E, F, G, H.

Các cạnh của hình hộp chữ nhật là: AB, BC, CD, DA, EF, FG, GH, HE, AE, BF, CG, DH.

Các đường chéo của hình hộp chữ nhật là: AG, BH, CE, DF.

Lời giải bài tập Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương hay, chi tiết khác:

Bài 10.3 trang 90 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương

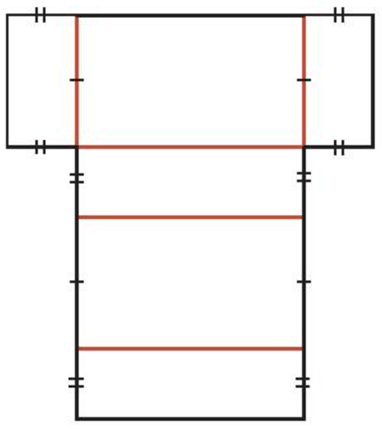
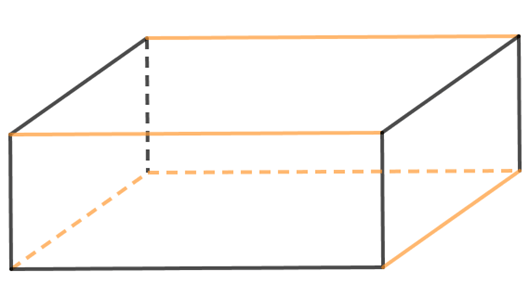
Bài 10.3 trang 90 Toán 7 Tập 2: Vẽ lên một miếng bìa hình khai triển của hình hộp chữ nhật (tương tự hình bên) với kích thước tùy chọn. Cắt rời hình đã vẽ rồi gấp theo đường màu cam để được một hình hộp chữ nhật.

Lời giải:

Gấp theo đường màu cam ta được hình hộp như sau:

Lời giải bài tập Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương hay, chi tiết khác:

Bài 10.4 trang 91 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương

Bài 10.4 trang 91 Toán 7 Tập 2: Một xe đông lạnh có thùng hàng dạng hình hộp chữ nhật, kích thước lòng thùng hàng dài 5,6 m, rộng 2 m, cao 2 m. Tính thể tích của lòng thùng hàng.

Lời giải:

Thể tích của lòng thùng hàng là: 5,6 . 2 . 2 = 22,4 (m³).

Vậy thể tích thùng hàng là 22,4 m³.

Lời giải bài tập Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương hay, chi tiết khác:

Bài 10.5 trang 91 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương

Bài 10.5 trang 91 Toán 7 Tập 2: Một hộp sữa tươi có dạng hình hộp chữ nhật với dung tích 1 lít, chiều cao 20 cm, chiều dài 10 cm.

a) Tính chiều rộng của hộp sữa.

b) Tính diện tích vật liệu dùng để làm vỏ hộp sữa? (Coi như phần mép hộp không đáng kể).

Lời giải:

Đổi 1 lít = 1 000 cm³.

a) Khi đó chiều rộng của hộp sữa là: 1 000 : 20 : 10 = 5 (cm).

Vậy chiều rộng của hộp sữa là 5 cm.

b) Diện tích vật liệu dùng để làm vỏ hộp sữa bằng tổng diện tích xung quanh và diện tích hai đáy của vỏ hộp.

Diện tích xung quanh của vỏ hộp là: 2(10 + 5). 20 = 600 (cm²).

Diện tích hai đáy của vỏ hộp là: 2.10.5 = 100 (cm²).

Diện tích vật liệu dùng để làm vỏ hộp sữa là: 600 + 100 = 700 (cm²).

Vậy diện tích vật liệu dùng để làm vỏ hộp sữa là 700 cm².

Lời giải bài tập Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương hay, chi tiết khác:

Bài 10.6 trang 91 Toán 7 Tập 2 - Kết nối tri thức

Giải Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương

Bài 10.6 trang 91 Toán 7 Tập 2: Một bể nước có dạng hình hộp chữ nhật với chiều dài 2 m. Lúc đầu bể không có nước. Sau khi đổ vào bể 120 thùng nước, mỗi thùng chứa 20 l nước thì mực nước của bể dâng cao 0,8 m.

a) Tính chiều rộng của bể nước.

b) Người ta đổ thêm 60 thùng nước nữa thì đầy bể. Hỏi bể cao bao nhiêu mét?

Lời giải:

Tổng lượng nước của 120 thùng nước là: 120 . 20 = 2 400 (l).

Đổi 2 400 l = 2,4 m³.

a) Khi đổ thêm 120 thùng nước, mỗi thùng 20l thì mức nước của bể dâng cao 0,8m nên 0,8 m là chiều cao của lượng nước trong bể.

Chiều rộng của bể nước là: 2,4 : 2 : 0,8 = 1,2 : 0,8 = 1,5 (m).

Vậy chiều rộng của bể nước là 1,5 m.

b) Lượng nước của 60 thùng nước là: 60. 20 = 1 200 (l).

Bể đầy nước thì chứa được 2 400 + 1 200 = 3 600 (l).

Đổi 3 600 l = 3,6 m³.

Chiều cao của bể nước là: 3,6 : 2 : 1,5 = 1,8 : 1,5 = 1,2 m.

Vậy bể cao 1,2 m.

Lời giải bài tập Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương hay, chi tiết khác:

Sách bài tập Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương - Kết nối tri thức

Với giải sách bài tập Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Bài 36.

Giải SBT Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương - Kết nối tri thức

Giải SBT Toán 7 trang 62 Tập 2

Vở thực hành Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương - Kết nối tri thức

Với giải vở thực hành Toán lớp 7 Bài 36: Hình hộp chữ nhật và hình lập phương sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập về nhà trong VTH Toán 7 Bài 36.

Giải vở thực hành Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương - Kết nối tri thức

Giải VTH Toán 7 trang 90 Tập 2

Hình hộp chữ nhật và hình lập phương (Lý thuyết Toán lớp 7) - Kết nối tri thức

Với tóm tắt lý thuyết Toán 7 Bài 36: Hình hộp chữ nhật và hình lập phương sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Hình hộp chữ nhật và hình lập phương (Lý thuyết Toán lớp 7) - Kết nối tri thức

Lý thuyết Hình hộp chữ nhật và hình lập phương

1. Hình hộp chữ nhật, hình lập phương

+ Hình hộp chữ nhật có 6 mặt là các hình chữ nhật, 8 đỉnh, 12 cạnh, 4 đường chéo, các cạnh bên song song và bằng nhau.

+ Hình lập phương là hình hộp chữ nhật có 6 mặt là các hình vuông.

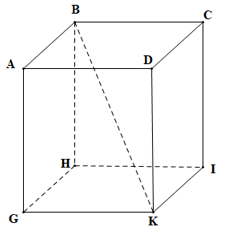
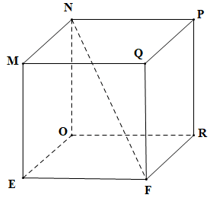
Ví dụ: Kể tên các đỉnh, cạnh, đường chéo, mặt bên, mặt đáy của hình hộp chữ nhật ABCD.GHIK và hình lập phương MNPQ.EORF (hình vẽ).

Hướng dẫn giải

a) Hình hộp chữ nhật:

- Hình hộp chữ nhật ABCD.GHIK có:

+) 8 đỉnh là A, B, C, D, G, H, I, K;

+) 12 cạnh là AB, BC, CD, DA, GH, HI, IK, KG, AG, BH, CI, DK;

+) 4 đường chéo là AI, BK, CG, DH;

+) 4 mặt bên là ABHG, BHIC, CIKD, ADKG và 2 mặt đáy là ABCD, GHIK. Các mặt bên và mặt đáy là các hình chữ nhật.

b) Hình lập phương:

- Hình lập phương MNPQ.EORF có :

+) 8 đỉnh là M, N, P, Q, E, O, R, F;

+) 12 cạnh là MN, NP, PQ, QM, EO, OR, RF, FE, ME, NO, PR, QF;

+) 4 đường chéo là MR, NF, PE, QO;

+) 4 mặt bên là MNOE, NORP, PRFQ, MEFQ và 2 mặt đáy là MNPQ, EORF. Các mặt bên và mặt đáy là các hình vuông.

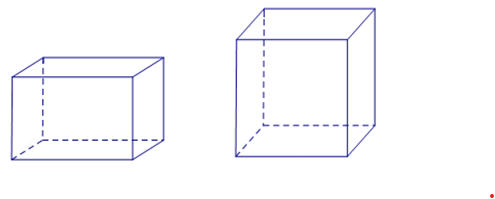
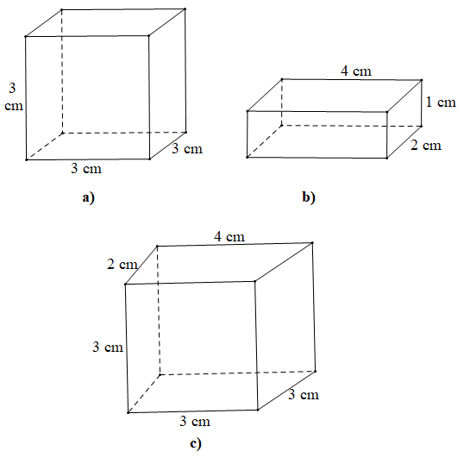
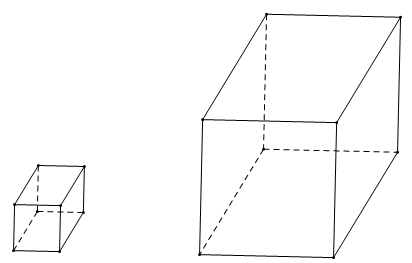
Ví dụ: Trong các hình sau hình nào là hình hộp chữ nhật, hình lập phương ?

Hướng dẫn giải

- Hình a) có 6 mặt đều là hình vuông cạnh 3 cm nên hình a) là hình lập phương.

- Hình b) có 2 mặt đáy, 4 mặt bên đều là hình chữ nhật và hình b) có ba kích thước khác nhau (1 cm, 2 cm, 4 cm) nên hình b) là hình hộp chữ nhật.

- Quan sát hình c) ta thấy mặt đáy là tứ giác có độ dài bốn cạnh là 2 cm, 3 cm, 3 cm và 4 cm. Do đó mặt đáy không phải là hình vuông hay hình chữ nhật,

Vậy hình c) không phải hình hộp chữ nhật, cũng không phải hình lập phương.

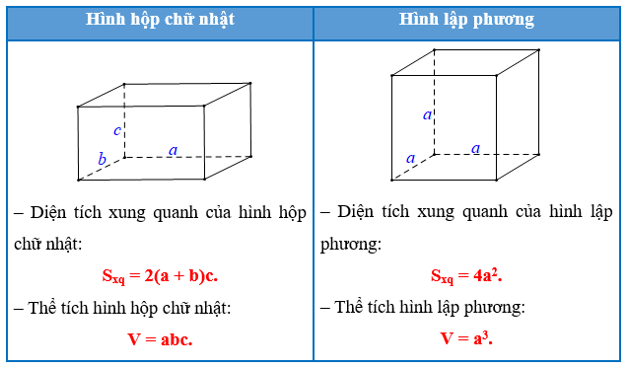
2. Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương

Chú ý: Khi tính diện tích, thể tích của một hình, các kích thước của nó phải cùng đơn vị độ dài.

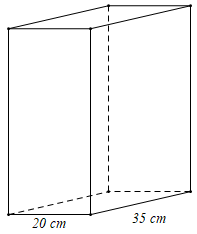
Ví dụ: Cho hình hộp chữ nhật có độ dài hai cạnh của đáy là 20 cm, 35 cm và chiều cao bằng tổng hai cạnh đáy. Tính diện tích xung quanh và thể tích của hình hộp chữ nhật trên.

Hướng dẫn giải

Chiều cao của hình hộp chữ nhật là: 20 + 35 = 55 (cm).

Diện tích xung quanh của hình hộp chữ nhật là:

S_xq = 2 . (20 + 35).55 = 6 050 (cm²).

Thể tích của hình hộp chữ nhật là:

V = 20 . 35 . 55 = 38 500 (cm³).

Vậy diện tích xung quanh và thể tích của hình hộp chữ nhật lần lượt là 6 050 cm² và 38 500 cm³.

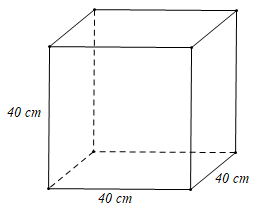
Ví dụ: Một thùng đựng đồ đa năng (không có nắp) có dạng hình lập phương cạnh 40 cm với khung bằng thép, đáy và các mặt bên được bọc bằng vải. Coi phần các mép vải khâu nổi không đáng kể. Tính diện tích vải để làm cái thùng đựng đồ đa năng đó.

Hướng dẫn giải

Diện tích xung quanh của hình lập phương là:

S_xq = 4. 40² = 6 400 (cm²).

Diện tích đáy của hình lập phương là:

S_đáy = 40² = 1 600 (cm²).

Diện tích vải cần dùng để làm cái thùng là:

6 400 + 1 600 = 8 000 (cm²)

Vậy cần 8 000 cm² vải để may một thùng đựng đồ đa năng đó.

Ví dụ: Hai chiếc khay đá gồm 15 hình lập phương nhỏ cạnh 3,5 cm (hình vẽ).

Hỏi tổng thể tích toàn bộ các viên đá lạnh đựng đầy trong hai khay là bao nhiêu?

Hướng dẫn giải

Thể tích một viên đá nhỏ là:

V = 3,5³ = 42,875 (cm³).

Một khay đá có 15 viên đá nhỏ nên hai khay đá có 2 . 15 = 30 viên đá nhỏ.

Thể tích của 30 viên đá trong hai khay đá đó là:

30 . 42,875= 1 286,25 (cm³).

Vậy tổng thể tích toàn bộ các viên đá lạnh đựng đầy trong hai khay là 1 286,25 cm³.

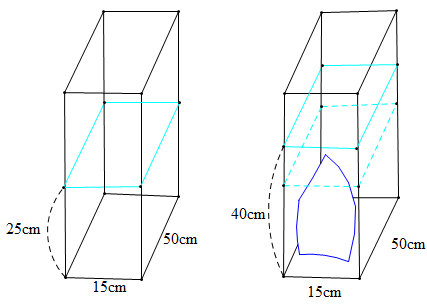
Ví dụ:Để tính thể tích một hòn đá bạn Mai làm như sau:

– Bạn ấy đã đổ nước vào một bể kính hình hộp chữ nhật có hai cạnh đáy là 15 cm và 50 cm, đo mực nước được 25 cm.

– Sau đó, bạn Mai đặt hòn đá vào bể thấy nước ngập hòn đá và mực nước lúc này là 40 cm.

Bạn Mai tính được thể tích của hòn đá bằng bao nhiêu?

Hướng dẫn giải

Thể tích nước trong bể kính lúc đầu là:

V = 15 . 50 . 25 = 18 750 (cm³).

Thể tích nước trong bể kính lúc sau là:

V = 15 . 50 . 40 = 30 000 (cm³).

Thể tích hòn đá là:

30 000 – 18 750 = 11 250 (cm³).

Vậy thể tích hòn đá là 11 250 cm³.

Bài tập Hình hộp chữ nhật và hình lập phương

Bài 1. Trong các đồ vật sau, đồ vật nào có dạng hình hộp chữ nhật, đồ vật nào có hình lập phương?

Lời giải

Đồ vật có dạng hình hộp chữ nhật là: quyển sách, hộp bánh quy, hộp giấy lụa.

Đồ vật có dạng hình lập phương là: Con xúc xắc, hộp quà.

Bài 2. Một bể bơi có chiều dài 20 m, chiều rộng 7 m, sâu 3 m. Hỏi người thợ phải dùng bao nhiêu viên gạch ốp lát để lát đáy và xung quanh thành bể đó? Biết rằng mỗi viên gạch có chiều dài 40 cm, rộng 25 cm và coi diện tích mạch vữa lát không đáng kể.

Hướng dẫn giải

Diện tích đáy bể là:

20 . 7 = 140 (m²).

Diện tích xung quanh thành bể là:

2 . (20 + 7) . 3 = 162 (m²).

Diện tích cần lát gạch là:

140 + 162 = 302 (m²).

Diện tích một viên gạch là:

40. 25 = 1 000 (cm²) = 0,1 (m²).

Số viên gạch ốp lát cần dùng là:

302 : 0,1 = 3 020 (viên)

Vậy số viên gạch ốp tường cần dùng 3 020 viên.

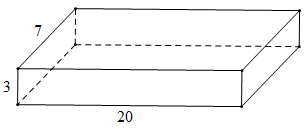
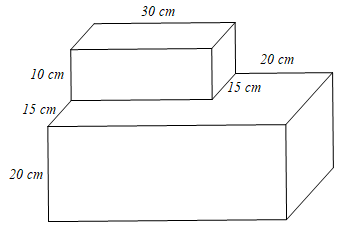
Bài 3. Cho một khối bê tông kích thước như hình vẽ sau:

a) Tính thể tích của khối bê tông đó.

b) Người ta muốn sơn khối bê tông đó trừ mặt tiếp giáp với đất, tính chi phí sơn biết mỗi mét vuông tốn 50 000 đồng.

Hướng dẫn giải

a) Chiều dài của hình hộp chữ nhật phía dưới là:

30 + 20 = 50 (cm).

Chiều rộng của hình hộp chữ nhật phía dưới là :

15 + 15 = 30 (cm).

Thể tích hình hộp chữ nhật phía dưới là:

50 . 30 . 20 = 30 000 (cm³).

Thể tích hình hộp chữ nhật phía trên là:

30 . 15 . 10 = 4 500 (cm³).

Thể tích của khối bê tông là:

30 000 + 4 500 = 34 500 (cm³).

Vậy thể tích khối bê tông là 34 500 cm³.

b) Diện tích xung quanh của hình hộp chữ nhật phía dưới là:

2 . (50 + 30) . 20 = 3 200 (cm²).

Diện tích xung quanh của hình hộp chữ nhật phía trên là:

2 . (30 + 15) . 10 = 900 (cm²).

Diện tích phần tiếp giáp giữa hai hình hộp chữ nhật chính là diện tích mặt đáy của hình hộp chữ nhật phía trên.

Do đó diện tích của các mặt nằm ngang cần sơn của khối bê tông bằng diện tích mặt đáy hình hộp chữ nhật phía dưới.

Diện tích đó là: 50 . 30 = 1 500 (cm²).

Diện tích của phần bê tông muốn sơn là:

3 200 + 900 + 1 500 = 5 600 (cm²) = 0,56 (m²).

Chi phí để sơn khối bê tông đó là:

0,56 . 50 000 = 28 000 (đồng)

Vậy muốn sơn khối bê tông cần chi phí là 28 000 đồng.

Bài 4. Một hình lập phương có cạnh 5 cm. Nếu cạnh của hình lập phương tăng lên ba lần thì thể tích tăng lên bao nhiêu lần?

Hướng dẫn giải

Cách 1:

Thể tích hình lập phương là:

5³ = 125 (cm³).

Cạnh hình lập phương mới là:

5 . 3 = 15 (cm).

Thể tích hình lập phương mới là: 15³ = 3 375 (cm³).

Thể tích hình lập phương mới tăng lên số lần là:

3375 : 125 = 27 (lần)

Vậy khi độ dài cạnh tăng lên 3 lần thì thể tích hình lập phương tăng lên 27 lần.

Cách 2:

Công thức tính thể tích của hình lập phương có cạnh là a (cm) là V = a³ (cm³).

Khi tăng độ dài cạnh hình lập phương lên 3 lần thì thể tích lúc này là:

(3a)³ = 3³ . a³ = 27a³ = 27V (cm³).

Vậy khi độ dài cạnh tăng lên 3 lần thì thể tích hình lập phương tăng lên 27 lần.

Bài 5. Một hình hộp chữ nhật có diện tích đáy bằng 1 800 cm². Chiều dài hơn chiều cao 40 cm và chiều dài cũng gấp ba lần chiều cao. Tính diện tích xung quanh và thể tích hình hộp đó.

Hướng dẫn giải

Gọi chiều cao của hình hộp chữ nhật là a (cm, a > 0).

Khi đó chiều dài của hình hộp chữ nhật là 3a (cm).

Khi đó chiều dài hơn chiều cao là 3a – a = 2a (cm).

Mà theo bài chiều dài hơn chiều cao 40 cm nên ta có 2a = 40

Do đó a = 20 (cm).

Khi đó chiều cao hình hộp chữ nhật là 20 cm.

Chiều dài hình hộp chữ nhật là:

20 + 40 = 60 (cm).

Chiều rộng hình hộp chữ nhật là:

1 800 : 60 = 30 (cm).

Diện tích xung quanh của hình hộp chữ nhật là:

2 . (60 + 30) . 20 = 3 600 (cm²).

Thể tích hình hộp chữ nhật là:

60 . 30 . 20 = 36 000 (cm³).

Vậy diện tích xung quanh và thể tích của hình hộp chữ nhật lần lượt là 3 600 cm² và 36 000 cm³.

Học tốt Hình hộp chữ nhật và hình lập phương

Các bài học để học tốt Hình hộp chữ nhật và hình lập phương Toán lớp 7 hay khác:

15 Bài tập Hình hộp chữ nhật và hình lập phương (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 7

Với 15 bài tập trắc nghiệm Hình hộp chữ nhật và hình lập phương Toán lớp 7 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 7.

15 Bài tập Hình hộp chữ nhật và hình lập phương (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 7

Xem thử

Chỉ 150k mua trọn bộ trắc nghiệm Toán 7 Kết nối tri thức (cả năm) có lời giải chi tiết, bản word trình bày đẹp mắt, dễ dàng chỉnh sửa: