Giải Toán 7 | No tags
Với giải bài tập Toán 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác sách Kết nối tri thức hay nhất, chi tiết giúp học sinh lớp 7 dễ dàng làm bài tập Toán Hình 7 Bài 37.
1. Hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác
HĐ1 trang 94 Toán 7 Tập 2: Trong thực tế, ta gặp những vật thể có hình dạng sau đây. Hãy quan sát và nhận xét một vài đặc điểm chung của các hình đó:
Lời giải:
Các hình này đều có mặt bên là các hình chữ nhật, các cạnh bên song song và bằng nhau, hai mặt đáy song song với nhau.
Lời giải bài tập Toán 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác hay, chi tiết khác:
HĐ2 trang 95 Toán 7 Tập 2: Một số yếu tố của hình lăng trụ đứng tứ giác được chỉ rõ trong Hình 10.19. Em hãy nêu các yếu tố tương tự của hình lăng trụ đứng tam giác trong Hình 10.20 và cho một vài nhận xét về các yếu tố đó.
Lời giải:
Trong hình lăng trụ đứng tam giác Hình 10.20 ta có:
- Hai mặt đáy MNP và M’N’P’ song song với nhau.
- Các mặt bên M’N’NM, M’P’PM, P’N’NP là các hình chữ nhật.
- Các cạnh bên N’N, M’M, P’P song song và bằng nhau.
Lời giải bài tập Toán 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác hay, chi tiết khác:
Thực hành trang 95 Toán 7 Tập 2: Cắt và gấp một miếng bìa thành hình lăng trụ đứng tam giác theo hướng dẫn sau:
Bước 1. Vẽ hình khai triển theo mẫu và cắt theo viền (H.10.22).
Bước 2. Gấp theo nét màu cam. Ta được hình lăng trụ (H.10.23).
Lời giải:
Học sinh thực hiện theo hướng dẫn.
Lời giải bài tập Toán 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác hay, chi tiết khác:
HĐ3 trang 96 Toán 7 Tập 2: Quan sát hình lăng trụ đứng tam giác ABC.A’B’C’ và hình khai triển của nó. Hãy chỉ ra sự tương ứng giữa các mặt bên với các hình chữ nhật của hình khai triển.
Lời giải:
Hình (1) là hình chữ nhật có độ dài 2 cạnh lần lượt là a và h nên hình (1) là mặt AA’C’C.
Hình (2) là hình chữ nhật có độ dài 2 cạnh lần lượt là b và h nên hình (2) là mặt BB’C’C.
Hình (3) là hình chữ nhật có độ dài 2 cạnh lần lượt là c và h nên hình (3) là mặt AA’B’B.
Lời giải bài tập Toán 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác hay, chi tiết khác:
HĐ4 trang 96 Toán 7 Tập 2: Tính tổng diện tích các hình chữ nhật (1), (2), (3) và so sánh với tích của chu vi đáy với chiều cao của hình lăng trụ đứng ở hình trên.
Lời giải:
Diện tích hình (1) là ah, diện tích hình (2) là bh, diện tích hình (3) là ch.
Tổng diện tích các hình (1), (2), (3) là ah + bh + ch = (a + b + c)h.
Hình lăng trụ đứng trên có chu vi đáy bằng a + b + c, chiều cao là h nên tổng diện tích các hình (1), (2), (3) bằng tích của chu vi đáy với chiều cao.
Lời giải bài tập Toán 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác hay, chi tiết khác:
Luyện tập 1 trang 97 Toán 7 Tập 2: Một lều chữ A dạng hình lăng trụ đứng có kích thước như Hình 10.26. Tính diện tích vải để làm hai mái và trải đáy của lều.
Lời giải:
Diện tích vải để làm hai mái và trải đáy của lều là:
(2 + 2 + 2) . 5 = 30 (m2).
Vậy diện tích vải cần dùng để làm hai mái và trải đáy của lều là 30 m2.
Lời giải bài tập Toán 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác hay, chi tiết khác:
Vận dụng trang 97 Toán 7 Tập 2: Một khúc gỗ dùng để chặn bánh xe (giúp xe không bị trôi khi dừng đỗ) có dạng hình lăng trụ đứng, đáy là hình thang cân có kích thước như Hình 10.27. Người ta sơn xung quanh khúc gỗ này (không sơn hai đầu hình thang cân). Mỗi mét vuông sơn chi phí hết 20 000 đồng. Hỏi sơn xung quanh như vậy hết bao nhiêu tiền?
Lời giải:
Diện tích sơn của khúc gỗ là: (15.3 + 30) . 60 = 4 500 (cm2).
Đổi 4 500 cm2 = 0,45 m2.
Sơn xung quanh khúc gỗ hết: 0,45 . 20 000 = 9 000 (đồng).
Vậy cần 9 000 đồng để sơn xung quanh khúc gỗ trên.
Lời giải bài tập Toán 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác hay, chi tiết khác:
Luyện tập 2 trang 98 Toán 7 Tập 2: Một chiếc khay đựng linh kiện bằng nhựa, có dạng hình lăng trụ đứng đáy là hình thang vuông với độ dài hai cạnh đáy là 30 cm, 40 cm và các kích thước như Hình 10.29. Tính thể tích của khay.
Lời giải:
Diện tích đáy của khay là: . (30 + 40) . 15 = 525 (cm2).
Thể tích của khay là: 525 . 20 = 10 500 (cm3).
Vậy thể tích của khay là 10 500 cm3.
Lời giải bài tập Toán 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác hay, chi tiết khác:
Thử thách nhỏ trang 98 Toán 7 Tập 2: Một bể bơi có hình dạng và kích thước như Hình 10.30. Hình dạng của bể bơi được ghép bởi một hình hộp chữ nhật và một hình lăng trụ đứng tam giác. Khi bể bơi đầy ắp nước thì nó chứa bao nhiêu mét khối nước (bỏ qua độ dày của thành bể).
Lời giải:
Thể tích của hình hộp chữ nhật là: 25 . 10 . 2 = 500 m3.
Diện tích đáy của hình lăng trụ đứng tam giác là: . 4 . 7 = 14 m2
Thể tích của hình lăng trụ đứng tam giác là: 14 . 10 = 140 m3.
Dung tích của bể bơi là: 500 + 140 = 640 m3.
Vậy dung tích của bể bơi là 640 m3.
Lời giải bài tập Toán 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác hay, chi tiết khác:
Bài 10.11 trang 98 Toán 7 Tập 2: Quan sát và gọi tên các mặt đáy, mặt bên, cạnh đáy, cạnh bên của hình lăng trụ đứng tam giác ở Hình 10.31.
Lời giải:
Các mặt đáy của hình lăng trụ tam giác trên là: ABC, MNP.
Các mặt bên của hình lăng trụ tam giác trên là: ABNM, ACPM, BCPN.
Các cạnh đáy của hình lăng trụ tam giác trên là: AB, AC, BC, MN, NP, PM.
Các cạnh bên của hình lăng trụ tam giác trên là: AM, BN, CP.
Lời giải bài tập Toán 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác hay, chi tiết khác:
Bài 10.12 trang 99 Toán 7 Tập 2: Quan sát Hình 10.32 và cho biết, cạnh nào trong các cạnh (1), (2), (3) ghép với cạnh AB để có được hình lăng trụ đứng?
Lời giải:
Ta thấy rằng trong ba cạnh (1), (2), (3) thì cạnh (1) có độ dài bằng với cạnh AB nên cạnh (1) ghép với cạnh AB để có hình lăng trụ đứng.
Lời giải bài tập Toán 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác hay, chi tiết khác:
Bài 10.13 trang 99 Toán 7 Tập 2: Tính diện tích xung quanh và thể tích của hình lăng trụ đứng trong Hình 10.33.
Lời giải:
Diện tích xung quanh của hình lăng trụ đứng trên là: (6 + 8 + 10) . 15 = 360 (cm2).
Diện tích đáy của hình lăng trụ đứng trên là: . 6 . 8 = 24 (cm2).
Thể tích của hình lăng trụ đứng trên là: 24 . 15 = 360 (cm3).
Vậy diện tích xung quanh của hình lăng trụ đứng trên là 360 cm2, thể tích của hình lăng trụ đó là 360 cm3.
Lời giải bài tập Toán 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác hay, chi tiết khác:
Bài 10.14 trang 99 Toán 7 Tập 2: Thùng một chiếc máy nông nghiệp có dạng hình lăng trụ đứng tứ giác như Hình 10.34. Đáy của hình lăng trụ đứng này (mặt bên của thùng hàng) là một hình thang vuông có độ dài đáy lớn 3 m, đáy nhỏ 1,5 m. Hỏi thùng có dung tích bao nhiêu mét khối?
Lời giải:
Diện tích đáy của thùng là: . (1,5 + 3) . 1,5 = 3,375 (m2).
Dung tích của thùng là: 3,375 . 2 = 6,75 (m3).
Vậy dung tích của thùng là 6,75 m3.
Lời giải bài tập Toán 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác hay, chi tiết khác:
Bài 10.15 trang 99 Toán 7 Tập 2: Một hình gồm hai hình lăng trụ đứng ghép lại với các kích thước ở Hình 10.35. Tính thể tích của lăng trụ.
Lời giải:
Thể tích của hình lăng trụ tứ giác là: 10 . 8 . 5 = 400 (cm3).
Diện tích đáy của hình lăng trụ tam giác là: . 3 . 10 = 15 (cm2).
Thể tích của hình lăng trụ tam giác là: 15 . 8 = 120 (cm3).
Tổng thể tích của lăng trụ là: 400 + 120 = 520 (cm3).
Vậy tổng thể tích của lăng trụ là 520 cm3.
Lời giải bài tập Toán 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác hay, chi tiết khác:
Bài 10.16 trang 99 Toán 7 Tập 2: Một hộp đựng khẩu trang y tế được làm bằng bìa cứng có dạng một hình hộp chữ nhật, kích thước như Hình 10.36.
a) Hãy tính thể tích của hộp.
b) Tính diện tích bìa cứng dùng để làm hộp (bỏ qua mép dán).
Lời giải:
a) Thể tích của hộp là: 8 . 20 . 10 = 1 600 (cm3).
Vậy thể tích của hộp là 1 600 cm3.
b) Diện tích xung quanh của hộp là: 2 . (20 + 10) . 8 = 480 (cm2).
Diện tích hai đáy của hộp là: 2 . 20 . 10 = 400 (cm2).
Diện tích bìa cứng dùng để làm hộp bằng tổng diện tích xung quanh và diện tích hai đáy của hộp.
Do đó diện tích bìa cứng dùng để làm hộp là: 480 + 400 = 880 (cm2).
Vậy diện tích bìa cứng dùng để làm hộp là 880 cm2.
Lời giải bài tập Toán 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác hay, chi tiết khác:
Với giải sách bài tập Toán 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Bài 37.
Với giải vở thực hành Toán lớp 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập về nhà trong VTH Toán 7 Bài 37.
Với tóm tắt lý thuyết Toán 7 Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.
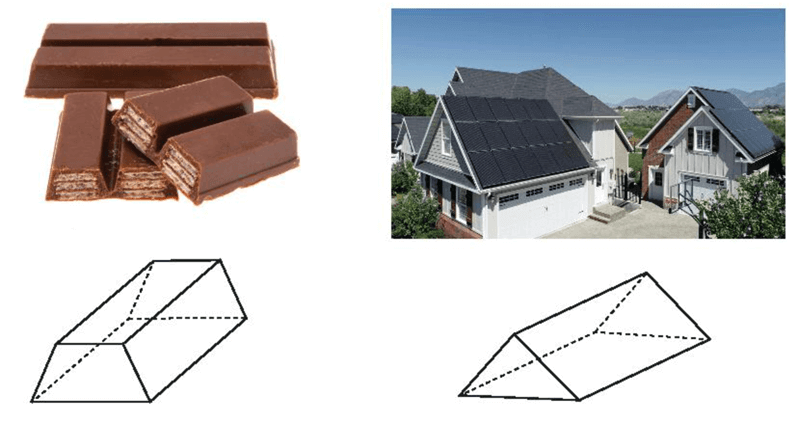
1. Hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác
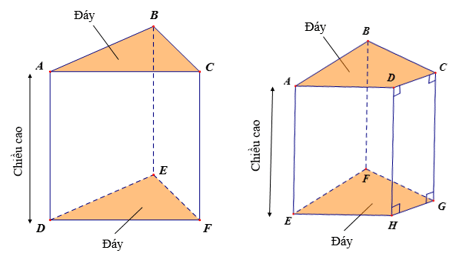
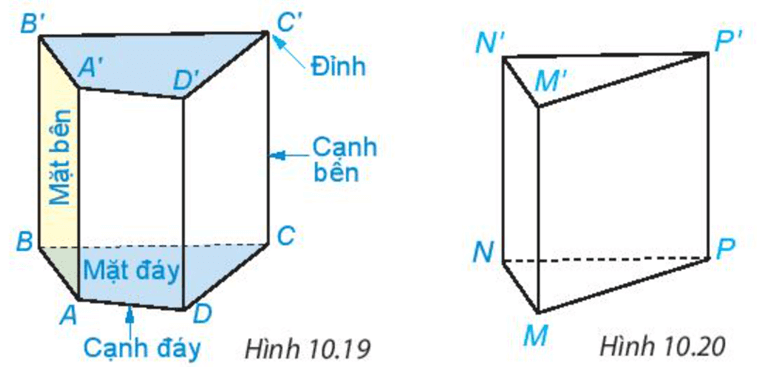
–Trong hình lăng trụ đứng tam giác (tứ giác):
+ Hai mặt đáy song song với nhau.
+ Các mặt bên là những hình chữ nhật.
+ Các cạnh bên song song và bằng nhau.
–Độ dài một cạnh bên gọi là chiều cao của lăng trụ đứng.
–Hình hộp chữ nhật và hình lập phương cũng là các hình lăng trụ đứng tứ giác
Chú ý:Sàn nhà và trần nhà là hình ảnh của hai mặt song song.
Ví dụ: Kể tên các đỉnh, cạnh đáy, cạnh bên, mặt bên, mặt đáy của các hình lăng trụ đứng sau:
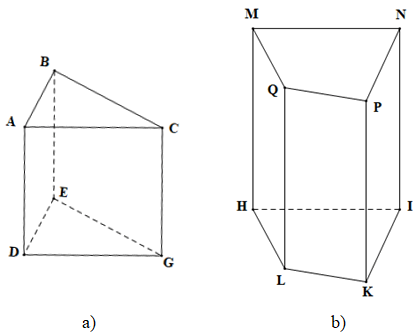
Hướng dẫn giải
Hình a) là hình lăng trụ đứng tam giác ABC.DEG có:
+ Các đỉnh là A, B, C, D, E, G;
+ Các cạnh đáy là AB, BC, AC, DE, EG, DG;
+ Các cạnh bên là AD, BE, CG;
+ Các mặt bên là các hình chữ nhật ABED, BCGE, ACGD;
+ Hai mặt đáy là các tam giác ABC, DEG.
Hình b) là hình lăng trụ đứng tứ giác MNPQ.HIKL có:
+ Các đỉnh là M, N, P, Q, H, I, K, L;
+ Các cạnh đáy là MN, NP, PQ, QM, HI, IK, KL, LH;
+ Các cạnh bên là MH, NI, PK, QL;
+ Các mặt bên là các hình chữ nhật MNIH, MQLH, QPKL, PNIK;
+ Hai mặt đáy là các tứ giác MNPQ, HIKL.
2. Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác
Ví dụ: Một khối gỗ có hình lăng trụ đứng tam giác, kích thước như hình vẽ:
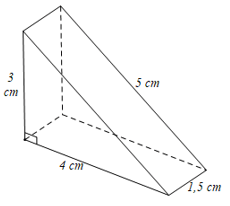
Người ta muốn sơn khối gỗ trên, hãy tính diện tích cần sơn.
Hướng dẫn giải
Diện tích cần sơn của khối gỗ là diện tích tất cả các mặt của hình lăng trụ đứng tam giác.
Diện tích xung quanh của khối gỗ dạng hình lăng trụ đứng là:
Sxq = (3 + 4 + 5) . 1,5 = 18 (cm2).
Diện tích một mặt đáy của khối gỗ dạng hình lăng trụ đứng là:
. 3 . 4 = 6 (cm2).
Diện tích tất cả các mặt của khối gỗ dạng hình lăng trụ đứng là:
18 + 2 . 6 = 30 (cm2).
Vậy diện tích cần sơn là 30 cm2.
Ví dụ: Tính diện tích xung quanh và thể tích của hình lăng trụ đứng tứ giác có đáy là hình thang cân với kích thước như hình vẽ sau:
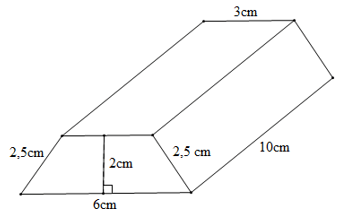
Hướng dẫn giải
Diện tích xung quanh của hình lăng trụ đứng tứ giác là:
(3 + 2,5 + 2,5 + 6) . 10 = 140 (cm2).
Diện tích mặt đáy của hình lăng trụ đứng là:
. (3 + 6) . 2 = 9 (cm2).
Thể tích của hình lăng trụ đứng tứ giác là:
9 . 10 = 90 (cm3).
Vậy diện tích xung quanh và thể tích của hình lăng trụ đứng tứ giác đó lần lượt là 140 cm2 và 90 cm3.
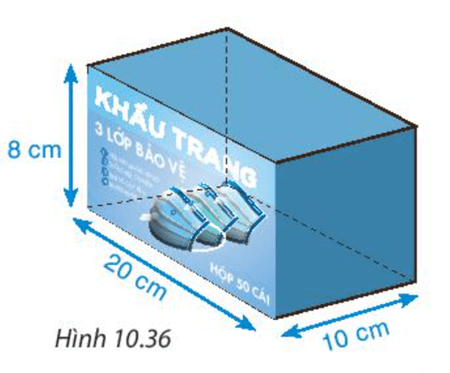
Ví dụ:Một chiếc hộp đèn có dạng hình lăng trụ đứng tam giác, có kích thước như sau:
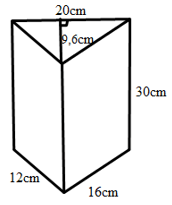
a) Tính diện tích xung quanh của chiếc hộp đèn.
b) Tính thể tích chiếc hộp đó.
Hướng dẫn giải
a) Diện tích xung quanh của chiếc hộp đèn là:
(12 + 16 + 20) . 30 = 1 440 (cm2).
b) Diện tích của mặt đáy là:
. 9,6 . 20 = 96 (cm2).
Thể tích chiếc hộp đó là:
96 . 30 = 2 880 (cm3)
Vậy diện tích xung quanh và thể tích của chiếc hộp đèn lần lượt là 1 440 cm2 và 2 880 cm3.
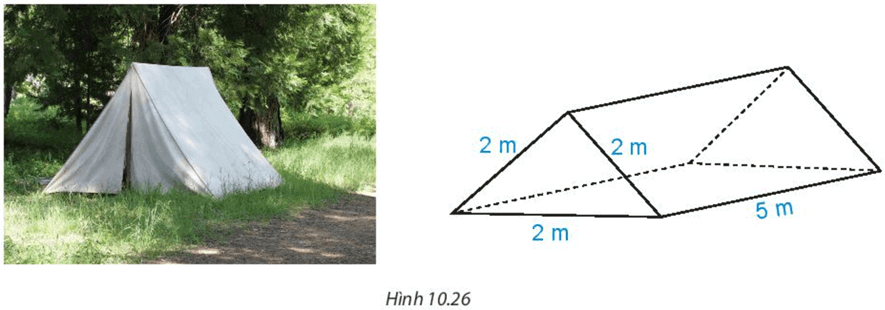
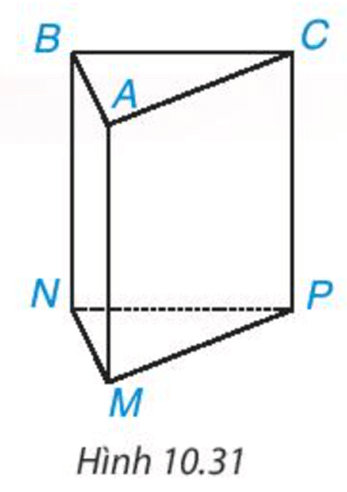
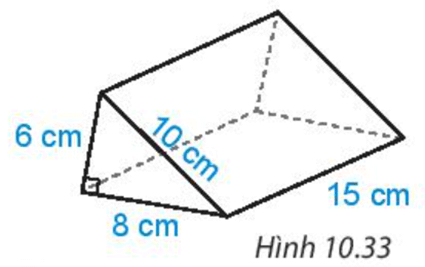
Bài 1. Một cái lều chữ A dạng hình lăng trụ đứng tam giác có kích thước như hình vẽ:
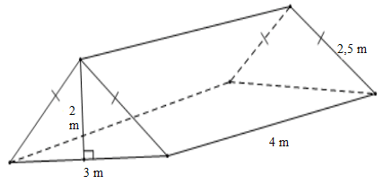
a) Tính thể tích khoảng không bên trong lều.
b) Biết lều phủ bạt bốn phía (trừ mặt tiếp đất), tính diện tích vải bạt cần có để dựng lều.
Hướng dẫn giải
a) Diện tích một mặt đáy của hình lăng trụ đứng tam giác là:
. 2 . 3 = 3 (m2)
Thể tích khoảng không bên trong lều là:
3 . 4 = 12 (m3).
Vậy thể tích khoảng không bên trong lều là 12 m3.
b) Diện tích xung quanh lăng trụ đứng tam giác là:
(2,5 + 2,5 + 3) . 4 = 32 (m2).
Diện tích tất cả các mặt của hình lăng trụ đứng tam giác là:
32+ 2 . 3 = 38(m2).
Diện tích mặt tiếp đất là: 3 . 4 = 12(m2).
Diện tích vải bạt cần có để dựng lều chính là diện tích tất cả các mặt của lăng trụ đứng tam giác trừ đi diện tích mặt tiếp đất. Do đó diện tích vải bạt cần là:
38 – 12 = 26 (m2).
Vậy diện tích vải bạt cần để dựng lều là 26 m2.
Bài 2. Cho hình lăng trụ đứng tam giác vuông có độ dài ba cạnh đáy là 6 cm, 8 cm, 10 cm. Biết diện tích xung quanh của hình lăng trụ đólà 288 cm2. Tính thể tích lăng trụ đó.
Hướng dẫn giải
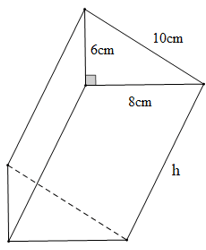
Diện tích một mặt đáy của hình lăng trụ đứng tam giác đó là:
. 6 . 8 = 24 (cm2).
Diện tích xung quanh của hình lăng trụ đứng tam giác đó được tính bởi:
(6 + 10 + 8) . h = 24h (cm2)
Mà diện tích xung quanh của hình lăng trụ đứng tam giác đó là 288 cm2 nên ta có:
24h = 288
Suy ra: h = 12 (cm).
Thể tích lăng trụ đó là:
24 . 12 = 288 (cm3)
Vậy thể tích lăng trụ đứng tam giác là 288 cm3.
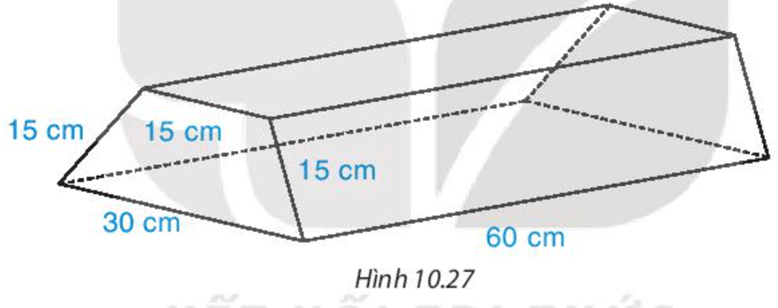
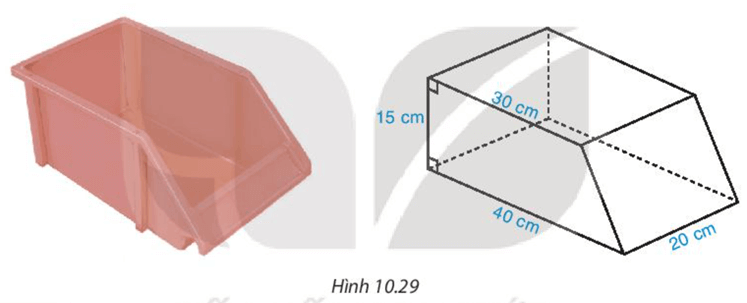
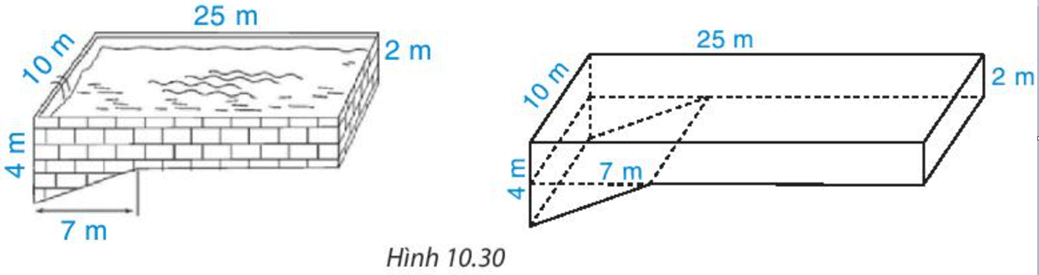
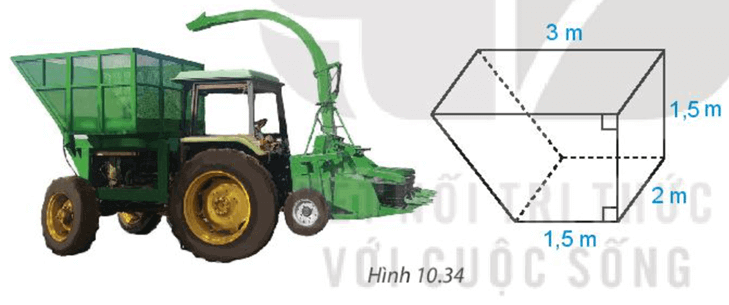
Bài 3. Một khối bê tôngcó kích thước như hình vẽ:
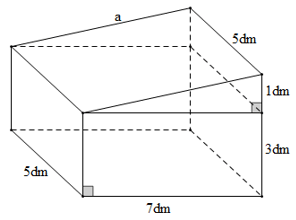
Hãy tính chi phí để đúc khối bê tông trên. Biết chi phí để đúc 1 m3 bê tông là 1,2 triệu đồng.
Hướng dẫn giải
Diện tích mặt đáy của khối bê tông có dạng hình lăng trụ đứng tứ giác là:
. (3 + 4) . 7 = 24,5 (dm2).
Thể tích khối bê tông đó là:
24,5 . 5 = 122,5 (dm3) = 0,1225 m3.
Chi phí để đúc khối bê tông đó là:
0,1225 . 1,2 = 0,135 (triệu đồng) = 135 000 đồng
Vậy chi phí để đúc khối bê tông đó là 135 000 đồng.
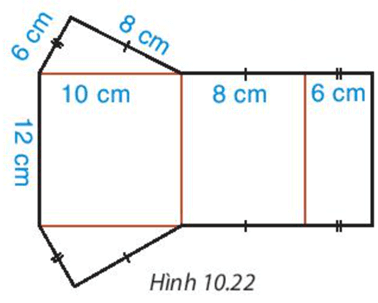
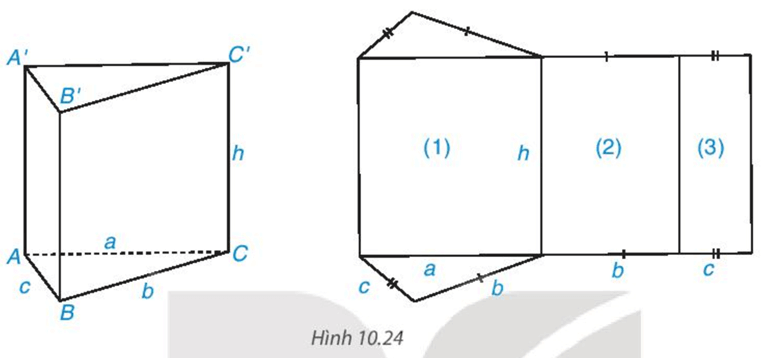
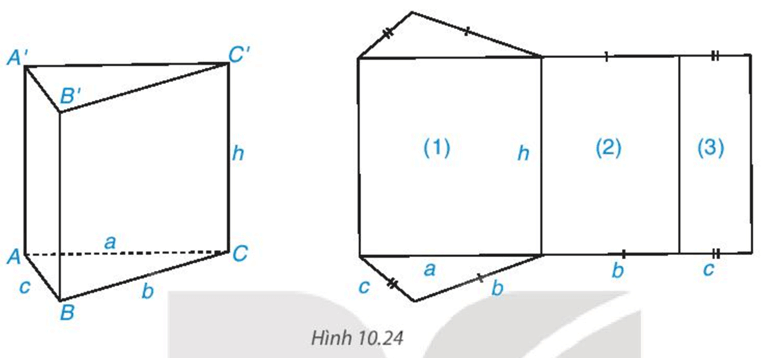
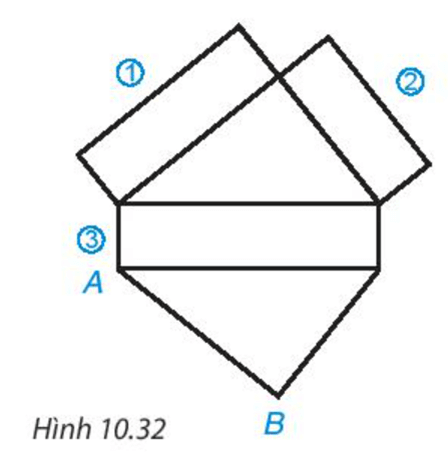
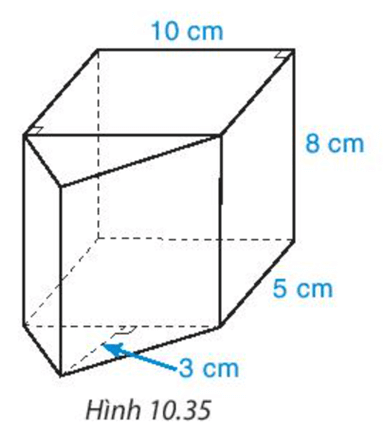
Bài 4. Cho tấm bìa có các kích thước như sau:
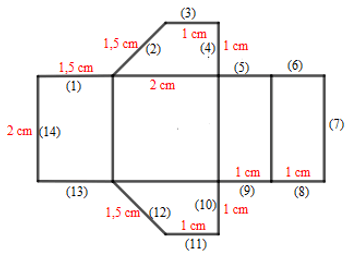
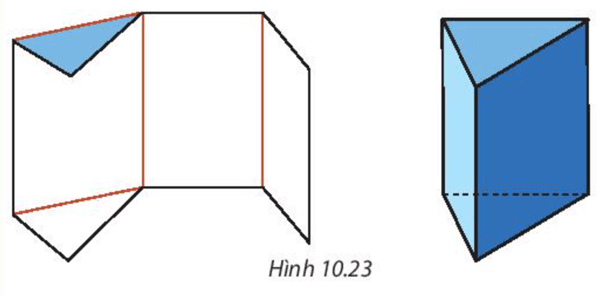
Phải gấp các cạnh nào của tấm bìa với nhau để được một hình lăng trụ đứng tứ giác? Cho biết chiều cao của tứ giác đó.
Hướng dẫn giải
Ta phải gấp các cặp cạnh sau đây với nhau để hình trên trở thành một hình lăng trụ đứng tứ giác: (1) và (2), (4) và (5), (3) và (6), (12) và (13), (9) và (10), (8) và (11), (7) và (14).
Khi đó ta có hình lăng trụ đứng tứ giác như sau:
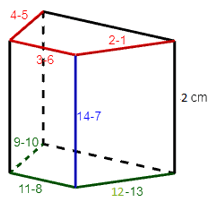
Vậy chiều cao của hình lăng trụ đứng trên là: 2 cm.
Các bài học để học tốt Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác Toán lớp 7 hay khác:
Với 15 bài tập trắc nghiệm Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác Toán lớp 7 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 7.
Chỉ 150k mua trọn bộ trắc nghiệm Toán 7 Kết nối tri thức (cả năm) có lời giải chi tiết, bản word trình bày đẹp mắt, dễ dàng chỉnh sửa: