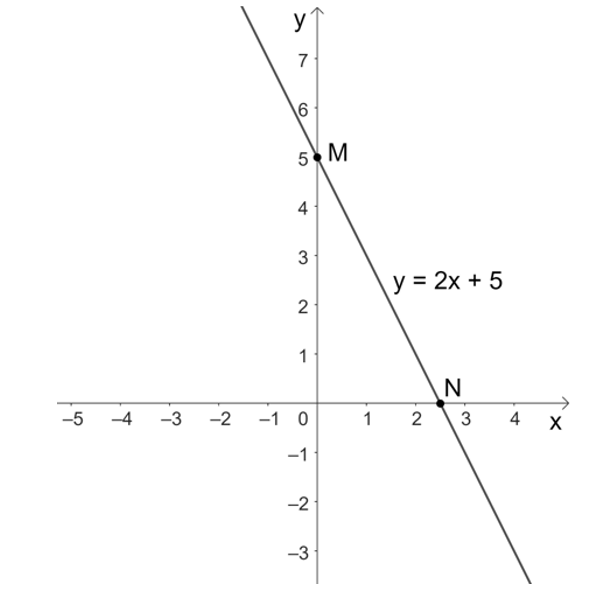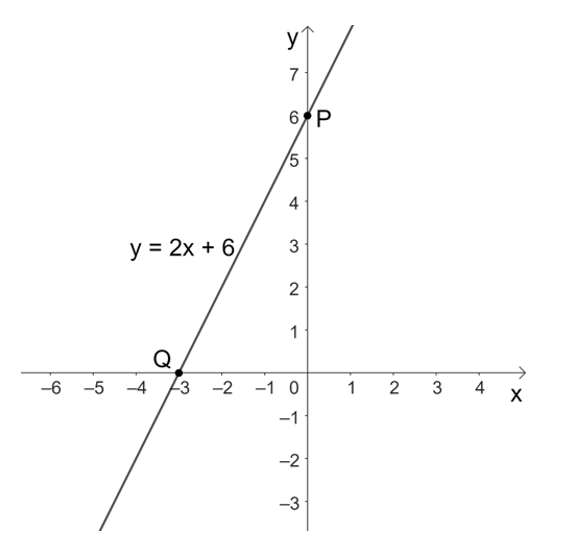Với giải bài tập Toán 8 Bài tập cuối chương 3 trang 78, 79 sách Cánh diều hay nhất, chi tiết giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 Bài tập cuối chương 3.

Giải Toán 8 Cánh diều Bài tập cuối chương 3 (trang 78, 79)

Video Giải Toán 8 Bài tập cuối chương 3 - Cô Vũ Chuyên (Giáo viên VietJack)

Giải Toán 8 trang 78

Bài 1 trang 78 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài tập cuối chương 3 - Cánh diều

Bài 1 trang 78 Toán 8 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai về hai đường thẳng

d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0)?

a) Nếu hai đường thẳng d và d’ song song với nhau thì a = a’, b ≠ b’.

b) Nếu hai đường thẳng d và d’ song song với nhau thì a = a’, b = b’.

c) Nếu hai đường thẳng d và d’ cắt nhau thì a ≠ a’.

d) Nếu hai đường thẳng d và d’ cắt nhau thì a ≠ a’, b ≠ b’.

Lời giải:

Với hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0)

• Nếu hai đường thẳng d và d’ song song với nhau thì a = a’, b ≠ b’.

Do đó, khẳng định a) đúng, khẳng định b) sai.

• Nếu hai đường thẳng d và d’ cắt nhau thì a ≠ a’.

Do đó, khẳng định c) đúng, khẳng định d) sai.

Lời giải bài tập Toán 8 Bài tập cuối chương 3 hay, chi tiết khác:

Bài 2 trang 78 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài tập cuối chương 3 - Cánh diều

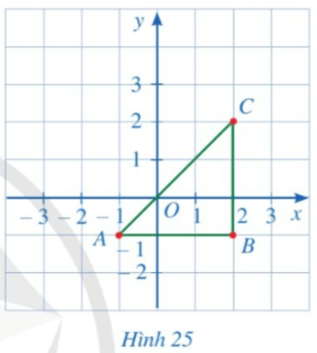
Bài 2 trang 78 Toán 8 Tập 1: Cho tam giác ABC như Hình 25.

a) Xác định tọa độ các điểm A, B, C.

b) Tam giác ABC có là tam giác vuông cân hay không?

c) Gọi D là điểm để tứ giác ABCD là hình vuông. Xác định tọa độ điểm D.

Lời giải:

a) • Hình chiếu của điểm A trên trục hoành là điểm – 1 và trên trục tung là điểm – 1.

Do đó, tọa độ điểm A là A(– 1; – 1).

• Hình chiếu của điểm B trên trục hoành là điểm 2 và trên trục tung là điểm – 1.

Do đó, tọa độ điểm B là B(2; – 1).

• Hình chiếu của điểm C trên trục hoành là điểm 2 và trên trục tung là điểm 2.

Do đó, tọa độ điểm C là C(2; 2).

Vậy tọa độ các điểm A, B, C lần lượt là A(– 1; – 1); B(2; – 1); C(2; 2).

b) Dựa vào các ô vuông trên hình vẽ, ta có AB // Ox; BC // Oy.

Mà Ox ⊥ Oy nên AB ⊥ BC hay $\widehat{B}=90°$.

Ta thấy AB = BC (= 3 ô vuông).

Xét tam giác ABC có $\widehat{B}=90°$ và AB = BC nên tam giác ABC là tam giác vuông cân.

c) Tam giác ABC vuông cân tại A (AB = BC; $\widehat{ABC}=90°$) nên để tứ giác ABCD là hình vuông thì $\widehat{DAB}=90°;\widehat{DCB}=90°$ và AB = BC = CD = DA.

Hay AB ⊥ AD; BC ⊥ CD và AB = BC = CD = DA.

• Qua điểm A, ta kẻ đường thẳng vuông góc với trục Oy.

• Qua điểm C, ta kẻ đường thẳng vuông góc với trục Ox.

 Hai đường thẳng này cắt nhau tại điểm D.

• AD cắt trục Oy tại điểm 1 nên điểm D có tung độ bằng 1.

• CD cắt trục Ox tại điểm 2 nên điểm D có hoành độ bằng 2.

Do đó, tọa điểm D là D(2; 1).

Vậy để tứ giác ABCD là hình vuông thì D(2; 1).

Lời giải bài tập Toán 8 Bài tập cuối chương 3 hay, chi tiết khác:

Bài 3 trang 78 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài tập cuối chương 3 - Cánh diều

Bài 3 trang 78 Toán 8 Tập 1: Càng lên cao không khí càng loãng nên áp suất khí quyển càng giảm. Chẳng hạn, các khu vực của Thành phố Hồ Chí Minh đều có độ cao sát mực nước biển nên có áp suất khí quyển là p = 760 mmHg; thành phố Puebla (Mexico) có độ cao h = 2 200 m so với mực nước biển nên có áp suất khí quyển là p = 550,4 mmHg. Người ta ước lượng được áp suất khí quyển p (mmHg) tương ứng với độ cao h (m) so với mực nước biển là một hàm số bậc nhất có dạng p = ah + b (a ≠ 0).

a) Xác định hàm số bậc nhất đó.

b) Cao nguyên Lâm Đồng có độ cao 650 m so với mực nước biển thì áp suất khí quyển là bao nhiêu mmHg (làm tròn đến hàng phần mười)?

Lời giải:

a) Các khu vực của Thành phố Hồ Chí Minh đều có độ cao sát mực nước biển nên có áp suất khí quyển là p = 760 mmHg hay ở độ cao h = 0 m thì có áp suất khí quyển là p = 760 mmHg.

Thay h = 0 m; p = 760 mmHg vào hàm số bậc nhất p = ah + b, ta được:

a . 0 + b = 760 hay b = 760.

Do đó hàm số bậc nhất có dạng p = ah + 760.

Mặt khác, thành phố Puebla (Mexico) có độ cao h = 2 200 m so với mực nước biển nên có áp suất khí quyển là p = 550,4 mmHg.

Thay h = 2 200 m; p = 550,4 mmHg vào hàm số bậc nhất p = ah + 760, ta được:

a . 2 200 + 760 = 550,4

2 200a = – 209,6

$a=-\frac{131}{1375}$.

Vậy hàm số bậc nhất cần tìm là $p=-\frac{131}{1375}h+760$.

b) Cao nguyên Lâm Đồng có độ cao 650 m so với mực nước biển thì áp suất khí quyển là

$p=-\frac{131}{1375}.650+760\approx \mathrm{698,1}$ (mmHg).

Vậy cao nguyên Lâm Đồng có độ cao 650 m so với mực nước biển thì áp suất khí quyển khoảng 698,1 mmHg.

Lời giải bài tập Toán 8 Bài tập cuối chương 3 hay, chi tiết khác:

Bài 4 trang 78 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài tập cuối chương 3 - Cánh diều

Bài 4 trang 78 Toán 8 Tập 1: Cho hai hàm số $y=-\frac{1}{2}x+3;y=2x-2.$

a) Vẽ đồ thị hai hàm số đó trên cùng một mặt phẳng tọa độ.

b) Gọi A, B lần lượt là giao điểm của hai đường thẳng $y=-\frac{1}{2}x+3;y=2x-2.$ với trục hoành và C là giao điểm của hai đường thẳng đó. Tính chu vi và diện tích của tam giác ABC (đơn vị đo trên các trục tọa độ là centimét).

Lời giải:

Cho hai hàm số $y=-\frac{1}{2}x+3;y=2x-2.$

a) * Hàm số $y=-\frac{1}{2}x+3$.

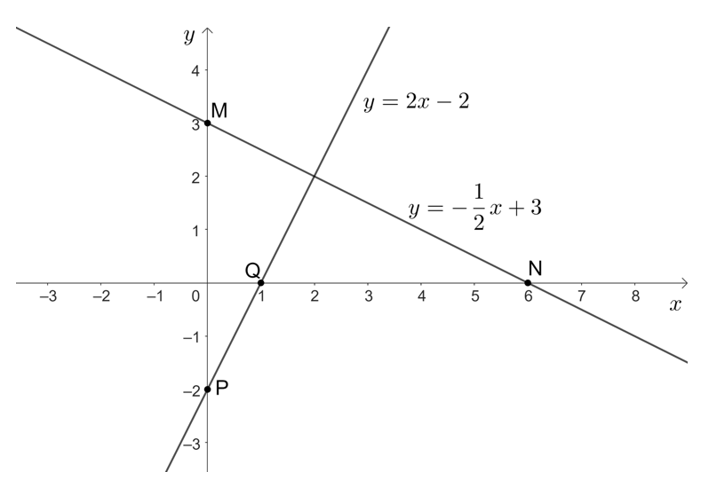
• Với x = 0 thì $y=-\frac{1}{2}.0+3=0+3=3$, ta được điểm M(0; 3) thuộc đồ thị của hàm số $y=-\frac{1}{2}x+3$

• Với y = 0 thì $-\frac{1}{2}x+3=0$ suy ra x = 6, ta được điểm N(6; 0) thuộc đồ thị của hàm số $y=-\frac{1}{2}x+3.$

Do đó, đồ thị của hàm số $y=-\frac{1}{2}x+3.$ là đường thẳng đi qua hai điểm M(0; 3) và N(6; 0).

* Hàm số y = 2x – 2.

• Với x = 0 thì y = 2 . 0 – 2 = 0 – 2 = – 2 , ta được điểm P(0; – 2) thuộc đồ thị của hàm số y = 2x – 2.

• Với y = 0 thì 2x – 2 = 0 suy ra x = 1, ta được điểm Q(1; 0) thuộc đồ thị của hàm số y = 2x – 2.

Do đó, đồ thị của hàm số y = 2x – 2 là đường thẳng đi qua hai điểm P(0; – 2) và Q(1; 0).

Ta vẽ đồ thị hai hàm số đó trên cùng một mặt phẳng tọa độ như sau:

b) Gọi A, B lần lượt là giao điểm của hai đường thẳng $y=-\frac{1}{2}x+3;y=2x-2$ với trục hoành và C là giao điểm của hai đường thẳng đó.

Khi đó A ≡ N; B ≡ Q.

Gọi H là hình chiếu của C trên AB hay CH là đường cao của tam giác ABC.

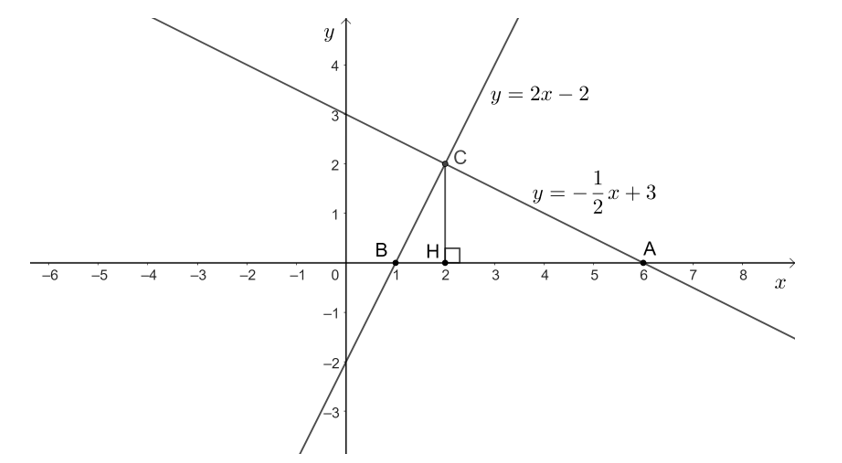
Ta có đồ thị hàm số như sau:

Dựa vào hình vẽ, ta có:

• Tọa độ điểm C là C(2; 2);

• H là hình chiếu của C trên Ox nên tọa độ điểm H là H(2; 0) suy CH = 2 cm.

• Độ dài AB bằng: 6 – 1 = 5 (cm).

• Độ dài BH bằng: 2 – 1 = 1 (cm).

• Độ dài AH bằng: 6 – 2 = 4 (cm).

Áp dụng định lý Pythagore, ta có:

• AC² = AH² + CH² = 4² + 2² = 20.

Suy ra $AC=\sqrt{20}$ cm.

• BC² = BH² + CH² = 1² + 2² = 5.

Suy ra $BC=\sqrt{5}$ cm.

Khi đó, chu vi tam giác ABC là:

$AB+BC+AC=5+\sqrt{5}+\sqrt{20}\approx \mathrm{11,71}$ (cm)

Diện tích tam giác ABC là:

$\frac{1}{2}AB.CH=\frac{1}{2}.5.2=5$ (cm²).

Vậy chu vi tam giác ABC khoảng 11, 71 cm và diện tích của tam giác ABC bằng 5 cm².

Lời giải bài tập Toán 8 Bài tập cuối chương 3 hay, chi tiết khác:

Bài 5 trang 79 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài tập cuối chương 3 - Cánh diều

Bài 5 trang 79 Toán 8 Tập 1: a) Biết rằng với x = 3 thì hàm số y = 2x + b có giá trị là 11. Tìm b và vẽ đồ thị của hàm số với giá trị b vừa tìm được.

b) Biết rằng đồ thị của hàm số y = ax + 6 đi qua điểm A(− 2; 2). Tìm a và vẽ đồ thị của hàm số với giá trị a vừa tìm được.

Lời giải:

a) Với x = 3 thì hàm số y = 2x + b có giá trị là 11 tức là

2 . 3 + b = 11

6 + b = 11

b = 11 – 6 = 5.

Khi đó, ta có đồ thị của hàm số y = 2x + 5.

• Với x = 0 thì y = 2 . 0 + 5 = 0 + 5 = 5, ta được điểm M(0; 5) thuộc đồ thị của hàm số y = 2x + 5.

• Với y = 0 thì 2x + 5 = 0 suy ra $x=\frac{-5}{2}$, ta được điểm $N\left(\frac{-5}{2};0\right)$ thuộc đồ thị của hàm số y = 2x + 5.

Do đó, đồ thị của hàm số y = 2x + 5 là đường thẳng đi qua hai điểm M(0; 5) và $N\left(\frac{-5}{2};0\right)$

Ta vẽ đồ thị của hàm số y = 2x + 5 như sau:

b) Đồ thị của hàm số y = ax + 6 đi qua điểm A(− 2; 2) nên – 2a + 6 = 2

Suy ra – 2a = – 4 do đó a = 2.

Khi đó, đồ thị của hàm số cần tìm là y = 2x + 6.

• Với x = 0 thì y = 2 . 0 + 6 = 0 + 6 = 6, ta được điểm P(0; 6) thuộc đồ thị của hàm số y = – 2x + 6.

• Với y = 0 thì 2x + 6 = 0 suy ra x = – 3, ta được điểm Q(– 3; 0) thuộc đồ thị của hàm số y = – 2x + 6.

Do đó, đồ thị của hàm số y = 2x + 6 là đường thẳng đi qua hai điểm P(0; 6) và Q(– 3; 0).

Ta vẽ đồ thị của hàm số y = 2x + 6 như sau:

Lời giải bài tập Toán 8 Bài tập cuối chương 3 hay, chi tiết khác:

Bài 6 trang 79 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài tập cuối chương 3 - Cánh diều

Bài 6 trang 79 Toán 8 Tập 1: >Tìm hàm số bậc nhất y = ax + b (a ≠ 0) trong mỗi trường hợp sau:

a) Đồ thị của hàm số đó đi qua điểm M(1; 3) và có hệ số góc bằng – 2;

b) Đồ thị của hàm số đó đi qua điểm N(– 1; 4) và song song với đường thẳng y = –3x – 1.

Lời giải:

a) Hàm số bậc nhất y = ax + b có hệ số góc bằng – 2 nên có dạng y = – 2x + b.

Đồ thị của hàm số y = – 2x + b đi qua điểm M(1; 3) thì ta có:

– 2 . 1 + b = 3 suy ra b = 5.

Vậy hàm số bậc nhất cần tìm là y = – 2x + 5.

b) Đồ thị của hàm số y = ax + b song song với đường thẳng y = –3x – 1 nên có dạng y = –3x + b.

Đồ thị của hàm số y = –3x + b đi qua điểm N(– 1; 4) thì ta có:

(–3) . (– 1) + b = 4

3 + b = 4

Suy ra b = 1.

Vậy hàm số bậc nhất cần tìm là y = – 3x + 1.

Lời giải bài tập Toán 8 Bài tập cuối chương 3 hay, chi tiết khác:

Bài 7 trang 79 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài tập cuối chương 3 - Cánh diều

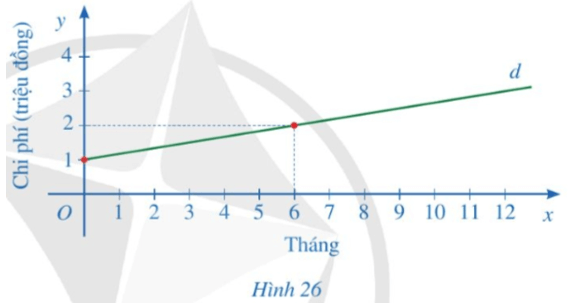
Bài 7 trang 79 Toán 8 Tập 1: Để sử dụng dịch vụ truyền hình cáp, người dùng phải trả một khoản phí ban đầu và phí thuê bao hằng tháng. Một phần đường thẳng d ở Hình 26 biểu thị tổng chi phí (đơn vị: triệu đồng) để sử dụng dịch vụ truyền hình cáp theo thời gian sử dụng của một gia đình (đơn vị: tháng).

a) Tìm hàm số bậc nhất sao cho đồ thị của hàm số là đường thẳng d.

b) Giao điểm của đường thẳng d với trục tung trong tình huống này có ý nghĩa gì?

c) Tính tổng chi phí mà gia đình đó phải trả khi sử dụng dịch vụ truyền hình cáp với thời gian 12 tháng.

Lời giải:

a) Gọi đường thẳng d có dạng y = ax + b.

Trong đó: y là chi phí sử dụng dịch vụ truyền hình cáp (triệu đồng) trong x (tháng).

• Với x = 0 thì y = 1 nên ta có 0x + b = 1 hay b = 1.

Khi đó, hàm số bậc nhất có dạng y = ax + 1.

• Với x = 6 thì y = 2 nên ta có 6a + 1 = 2 hay 6a = 1 suy ra $a=\frac{1}{6}$.

Vậy hàm số bậc nhất biểu diễn đường thẳng d là $y=\frac{1}{6}x+1$.

b) Giao điểm của đường thẳng d với trục tung trong tình huống này là chi phí ban đầu để sử dụng dịch vụ truyền hình cáp là 1 triệu đồng.

c) Tổng chi phí mà gia đình đó phải trả khi sử dụng dịch vụ truyền hình cáp với thời gian 12 tháng là:

$\frac{1}{6}.12+1=2+1=3$ (triệu đồng).

Vậy tổng chi phí mà gia đình đó phải trả khi sử dụng dịch vụ truyền hình cáp với thời gian 12 tháng là 3 triệu đồng.

Lời giải bài tập Toán 8 Bài tập cuối chương 3 hay, chi tiết khác:

Bài 8 trang 79 Toán 8 Tập 1 Cánh diều

Giải Toán 8 Bài tập cuối chương 3 - Cánh diều

Bài 8 trang 79 Toán 8 Tập 1: Một kho chứa 60 tấn xi măng, mỗi ngày đều xuất đi m (tấn) với 0 < m < 60. Gọi y (tấn) là khối lượng xi măng còn lại trong kho sau x ngày xuất hàng.

a) Chứng tỏ rằng y là hàm số bậc nhất của biến x, tức là y = ax + b (a ≠ 0).

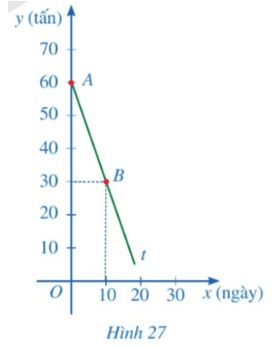
b) Trong Hình 27, tia At là một phần đường thẳng y = ax + b. Tìm a, b. Từ đó hãy cho biết trong kho còn lại bao nhiêu tấn xi măng sau 15 ngày.

Lời giải:

a) Theo đề bài, mỗi ngày đều xuất đi m (tấn) với 0 < m < 60.

Khi đó, khối lượng xi măng sau x ngày xuất hàng là: mx (tấn).

Khối lượng xi măng còn lại trong kho sau x ngày xuất hàng là: 60 – mx (tấn)

Mà y (tấn) cũng là khối lượng xi măng còn lại trong kho sau x ngày xuất hàng.

Do đó, y = 60 – mx hay y = – mx + 60.

Vậy y là hàm số bậc nhất của biến x.

b) Trong Hình 27, ta thấy:

• Điểm A(0; 60):

Với x = 0 thì y = 60 nên ta có: 0x + b = 60 hay b = 60.

Khi đó, đường thẳng cần tìm có dạng y = ax + 60.

• Điểm B(10; 30):

Với x = 10 thì y = 30 nên ta có: 10a + 60 = 30 hay 10a = – 30 suy ra a = – 3.

Khi đó, đường thẳng cần tìm có dạng y = – 3x + 60.

Do đó, số tấn xi măng trong kho còn lại sau 15 ngày là: – 3 . 15 + 60 = 15 (tấn).

Vậy a = – 3; b = 60 và trong kho còn lại 15 tấn xi măng sau 15 ngày.

Lời giải bài tập Toán 8 Bài tập cuối chương 3 hay, chi tiết khác:

Sách bài tập Toán 8 Cánh diều Bài tập cuối chương 3

Với giải sách bài tập Toán 8 Bài tập cuối chương 3 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 8 Bài tập cuối chương 3.

Giải SBT Toán 8 Bài tập cuối chương 3 - Cánh diều

Tổng hợp Lý thuyết Toán 8 Chương 3 Cánh diều

Tổng hợp lý thuyết Toán 8 Chương 3: Hàm số và đồ thị sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Tổng hợp Lý thuyết Toán 8 Chương 3 Cánh diều

Lý thuyết Tổng hợp Lý thuyết Toán 8 Chương 3

1. Định nghĩa hàm số

Nếu đại lượng y phụ thuộc vào đại lượng x (x thay đổi) sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số.

Chú ý:

+ Khi x thay đổi mà y luôn nhận một giá trị thì y được gọi là hàm hằng.

+ Hàm số có thể cho bằng công thức, bằng bảng.

+ Khi y là hàm số của x, ta có thể viết y = f(x), y = g(x),…

2. Giá trị của hàm số

Cho hàm số y = f(x) xác định tại x = a. Giá trị tương ứng của hàm số f(x) khi x = a được gọi là giá trị của hàm số y = f(x) tại x = a, kí hiệu là f(a).

3. Mặt phẳng tọa độ

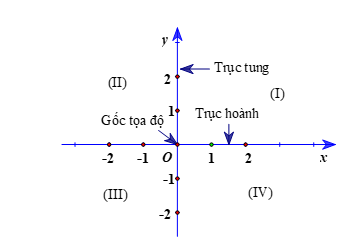
Trên mặt phẳng, ta vẽ hai trục số Ox, Oy vuông góc với nhau và cắt nhau tại gốc O của mỗi trục. Khi đó ta có hệ trục tọa độ Oxy.

Trục Ox, Oy gọi là các trục tọa độ, Ox gọi là trục hoành, Oy gọi là trục tung. O gọi là gốc tọa độ.

Mặt phẳng có hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ Oxy.

Chú ý:

- Hai trục tọa độ chia mặt phẳng thành bốn góc: góc phần tư thứ I, góc phần tư thứ II, góc phần tư thứ III, góc phần tư thứ IV theo thứ tự ngược chiều quay của kim đồng hồ.

- Các đơn vị độ dài trên hai trục tọa độ được chọn bằng nhau (nếu không có lưu ý gì thêm).

4. Tọa độ của một điểm trong mặt phẳng tọa độ

Cho điểm M trong mặt phẳng tọa độ Oxy. Giả sử hình chiếu của điểm M lên trục hoành Ox là điểm a trên trục số Ox, hình chiếu của điểm M lên trục tung Oy là điểm b trên trục số Oy.

Cặp số (a; b) gọi là tọa độ của điểm M, a là hoành độ và b là tung độ của điểm M.

Điểm M có tọa độ (a; b) được kí hiệu là M(a; b).

Chú ý:

- Trong mặt phẳng tọa độ Oxy, mỗi điểm M xác định một cặp số (a; b). Ngược lại, mỗi cặp số (a; b) xác định một điểm M.

- Điểm nằm trên trục hoành có tung độ bằng 0.

- Điểm nằm trên trục tung có hoành độ bằng 0.

5. Đồ thị của hàm số

Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng (x; f(x)) trên mặt phẳng tọa độ.

6. Định nghĩa hàm số bậc nhất y = ax + b (a ≠ 0)

Hàm số bậc nhất là hàm số được cho bởi công thức y = ax +b, trong đó a, b là các số cho trước và a khác 0.

Chú ý: Khi b = 0, ta có hàm số y = ax.

7. Đồ thị của hàm số bậc nhất

Định nghĩa: Đồ thị của hàm số y = ax + b (a ≠ 0) là một đường thẳng.

Chú ý:

- Đồ thị của hàm số y = ax + b (a ≠ 0) còn được gọi là đường thẳng y = ax + b (a ≠ 0).

- Đồ thị của hàm số y = ax + b (a ≠ 0) là một đường thẳng cắt trục tung tại điểm có tung

8. Cách vẽ đồ thị của hàm số bậc nhất

8.1. Cách vẽ đồ thị hàm số y = ax (a ≠ 0)

Cách vẽ:

Để vẽ đồ thị của hàm số y = ax (a ≠ 0), ta có thể xác định điểm A(1; a) rồi vẽ đường thẳng đi qua hai điểm O và A.

8.2. Cách vẽ đồ thị hàm số y = ax + b (a ≠ 0; b ≠ 0)

Cách vẽ:

Để vẽ đồ thị của hàm số y = ax + b (a ≠ 0; b≠ 0), ta có thể xác định hai điểm P(0; b) và Q $\left(\frac{-b}{a};0\right)$ rồi vẽ đường thẳng đi qua hai điểm đó.

9. Hệ số góc của đường thẳng y = ax + b (a ≠ 0)

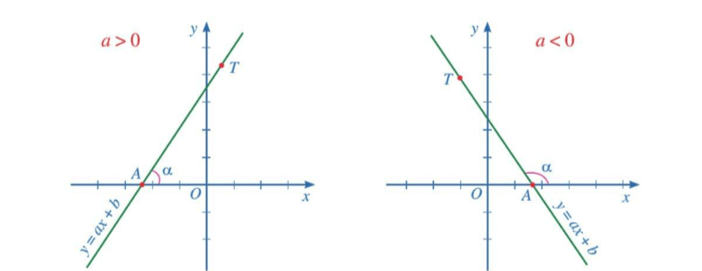
9.1. Góc tạo bởi đường thẳng y = ax + b (a ≠ 0) và trục Ox

Trong mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a ≠0). Gọi A là giao điểm của đường thẳng y = ax + b và trục Ox. T là một điểm thuộc đường thẳng y = ax + b và có tung độ dương.

Góc α tạo bởi hai tia Ax và AT gọi là góc tạo bởi đường thẳng y = ax + b và trục Ox (hoặc nói đường thẳng y = ax + b tạo với trục Ox một góc α).

9.2. Hệ số góc

Định nghĩa: Trên mặt phẳng tọa độ Oxy, cho đường thẳng y = ax + b (a ≠ 0). Hệ số a gọi là hệ số góc của đường thẳng y = ax + b (a ≠ 0).

Chú ý:

- Khi hệ số a > 0 thì góc tạo bởi đường thẳng y = ax + b (a ≠ 0) và trục Ox là góc nhọn. Hệ số a càng lớn thì góc càng lớn.

- Khi hệ số a < 0 thì góc tạo bởi đường thẳng y = ax + b (a ≠ 0) và trục Ox là góc tù. Hệ số a càng lớn thì góc càng lớn.

9.3. Ứng dụng của hệ số góc

Cách nhận biết vị trí tương đối của hai đường thẳng trong mặt phẳng tọa độ Oxy:

Cho hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠ 0).

a) Nếu d song song với d’ thì a = a’; b ≠ b’. Ngược lại, nếu a = a’; b ≠ b’ thì d song song với d’.

b) Nếu d trùng với d’ thì a = a’; b = b’. Ngược lại, nếu a = a’; b = b’ thì d trùng với d’.

c) Nếu d và d’ cắt nhau thì a ≠ a’. Ngược lại, nếu a ≠ a’ thì d và d’ cắt nhau.

Bài tập Tổng hợp Lý thuyết Toán 8 Chương 3

Bài 1. Các giá trị tương ứng của hai đại lượng x và y được cho trong bảng sau:

Đại lượng y có phải là hàm số của đại lượng x không?

Hướng dẫn giải

Đại lượng y là hàm số của đại lượng x vì mỗi giá trị của x chỉ xác định đúng một giá trị của y.

Bài 2. Các giá trị tương ứng của hai đại lượng x và y được cho trong bảng sau:

Đại lượng y có phải là hàm số của đại lượng x không?

Hướng dẫn giải

Đại lượng y không là hàm số của đại lượng x vì với giá trị x = 3 thì y nhận hai giá trị là 2 và 5.

Bài 3. Cho hàm số y = f(x) = 3x. Tính f(1); f(−2); $f\left(\frac{1}{3}\right)$ .

Hướng dẫn giải

f(1) = 3.1 = 3; f(−2) = 3.(−2) = −6 ; $f\left(\frac{1}{3}\right)=3.\frac{1}{3}=1$ .

Bài 4. Thời gian t (giờ) của một vật chuyển động đều trên quãng đường 20 km tỉ lệ nghịch với tốc độ v (km/h) của nó theo công thức $t=\frac{20}{v}$ . Đại lượng t có phải là hàm số của đại lượng v hay không? Nếu có, tính thời gian chuyển động của vật đó biết tốc độ của vật là 40 km/h?

Hướng dẫn giải

Đại lượng t là hàm số của đại lượng v vì mỗi giá trị của v ta nhận được chỉ một giá trị của t.

Với v = 40 km/h thì $t=\frac{20}{40}=\frac{1}{2}$  (giờ).

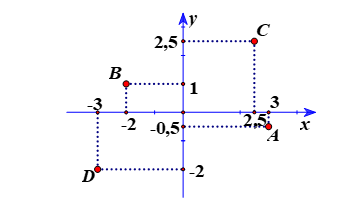
Bài 5. Vẽ mặt phẳng tọa độ Oxy và đánh dấu vị trí các điểm sau trên đó A(3; −0,5), B(−2; 1), C(2,5; 2,5), D(−3; −2).

Hướng dẫn giải

Cách xác định:

- Từ điểm biểu diễn hoành độ của điểm cho trước, kẻ một đường thẳng song song với trục tung.

- Tử điểm biểu diễn tung độ của điểm cho trước, kẻ một đường thẳng song song với trục hoành.

- Giao điểm của hai đường thẳng vừa dựng là điểm phải tìm.

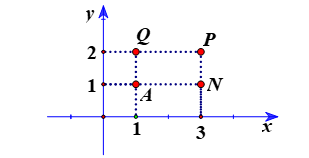
Bài 6. Viết tọa độ các điểm A, N, P, Q trong hình bên dưới.

Hướng dẫn giải

Cách xác định:

- Từ điểm đã cho kẻ đường thẳng song song với trục tung, cắt trục hoành tại một điểm biểu diễn hoành độ của điểm đó.

- Từ điểm đã cho kẻ đường thẳng song song với trục hoành, cắt trục tung tại một điểm biểu diễn tung độ của điểm đó.

- Hoành độ và tung độ tìm được là tọa độ của điểm đã cho.

Từ đó, ta các định được tọa độ các điểm là: A(1; 1), N(3; 1), P(3; 2), Q(1; 2).

Bài 7. Xác định các hệ số của x, hệ số tự do trong mỗi hàm số bậc nhất sau:

a) y = 3x – 4;

b) y = −x + 2;

c) $y=\frac{x}{2}$

Hướng dẫn giải

a) Hệ số của x là 3; hệ số tự do là −4.

b) Hệ số của x là −1; hệ số tự do là 2.

c) Hệ số của x là $\frac{1}{2}$ ; hệ số tự do là 0.

Bài 8. Cho hàm số bậc nhất f(x) = x −1. Tính f (1); f(0); f(−2).

Hướng dẫn giải

f(1) = 1 −1 = 0; f(0) = 0 −1 = −1; f(−2) = −2 −1 = −3.

Vậy f(1) = 0; f(0) = −1; f(−2) = −3.

Bài 9. Giá cước điện thoại cố định của một hãng viễn thông bao gồm cước thuê bao là 22000 đồng/tháng và cước gọi là 800 đồng/phút.

a) Lập công thức tính số tiền cước điện thoại y (đồng) phải trả trong tháng khi gọi x phút?

b) Tính số tiền cước điện thoại phải trả khi gọi 75 phút?

c) Nếu số tiền cước điện thoại phải trả là 94 000 đồng thì trong tháng đó thuê bao đã gọi bao nhiêu phút?

Hướng dẫn giải

a) Công thức tính số tiền cước điện thoại y (đồng) phải trả trong tháng khi gọi x phút là: y = 800x + 22 000.

b) Số tiền cước điện thoại phải trả khi gọi 75 phút là:

y = 800 . 75 + 22 000 = 82 000 (đồng).

Vậy số tiền cước điện thoại phải trả khi gọi 75 phút là 82 000 đồng.

c) Số tiền cước điện thoại phải trả là 94000 đồng thì trong tháng đó thuê bao đã gọi số phút là:

94 000 = 800.x + 22 000

800x = 94 000 − 22 000 

800x = 72 000 

Do đó x = 90.

Vậy nếu số tiền cước điện thoại phải trả là 94 000 đồng thì trong tháng đó thuê bao đã gọi 90 phút.

Bài 10. Chỉ ra các cặp đường thẳng cắt nhau và các cặp đường thẳng song song trong các đường thẳng sau: y = 3x + 1; y = 3x; y = −2x – 2.

Hướng dẫn giải

Cặp đường thẳng song song là: y = 3x + 1; y = 3x.

Cặp đường thẳng cắt nhau là: y = 3x + 1 và y = −2x – 2; y = 3x và y = −2x – 2.

Bài 11. Vẽ đồ thị của các hàm số y = 3x; y = − x − 2 trên cùng một mặt phẳng tọa độ?

Hướng dẫn giải

+ Với x = 1 thì y = 3, ta được điểm A(1; 3) thuộc đồ thị hàm số y = 3x.

Vẽ đồ thị hàm số y = 3x là đường thẳng đi qua gốc tọa độ và điểm A.

+ Với x = 0 thì y = −2, ta được điểm P(0; −2) thuộc đồ thị hàm số y = − x − 2.

Với y = 0 thì x = −2, ta được điểm Q(−2; 0) thuộc đồ thị hàm số y = − x − 2.

Vẽ đồ thị hàm số y = − x – 2 là đường thẳng đi qua hai điểm P và Q.

Bài 12.

a) Xác định đường thẳng y = ax + b (a ≠ 0) có hệ số góc bằng −1 và đi qua điểm M(1; 2)?

b) Xác định đường thẳng y = ax + b (a ≠ 0) đi qua điểm M(1; 3) và song song với đường thẳng y = 2x?

Hướng dẫn giải

a) Vì đường thẳng y = ax + b (a ≠ 0) có hệ số góc bằng −1 nên đường thẳng có dạng

y = −x + b.

Vì đường thẳng y = −x + b đi qua điểm M(1; 2) nên ta có: 2 = −1 + b hay b = 3.

Vậy y = −x + 3.

b) Vì đường thẳng y = ax + b (a ≠ 0) song song với đường thẳng y = 2x nên đường thẳng có dạng: y = 2x + b.

Mà đường thẳng y = 2x + b đi qua điểm M(1; 3) nên 3 = 2.1 + b hay b = 1.

Vậy y = 2x +1.

Học tốt Toán 8 Chương 3

Các bài học để học tốt tổng hợp Toán 8 Chương 3 Toán lớp 8 hay khác:

30 Bài tập tổng hợp Toán 8 Chương 3 Kết nối tri thức có lời giải

Với 30 bài tập trắc nghiệm tổng hợp Toán lớp 8 Chương 3: Hàm số và đồ thị có đáp án và lời giải chi tiết đầy đủ các mức độ sách Cánh diều sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 8.

30 Bài tập tổng hợp Toán 8 Chương 3 Kết nối tri thức có lời giải

Nội dung đang được cập nhật ...

Xem thêm bài tập trắc nghiệm Toán lớp 8 Cánh diều có đáp án hay khác: