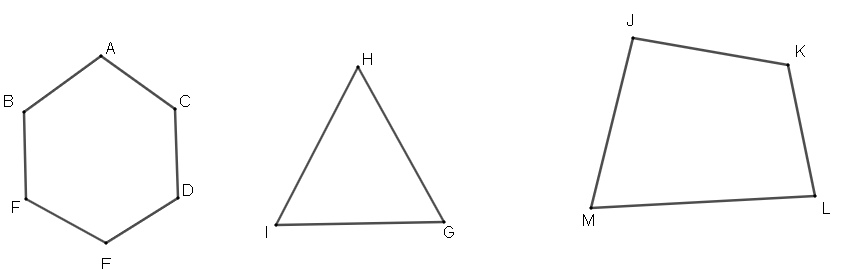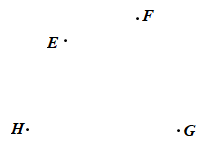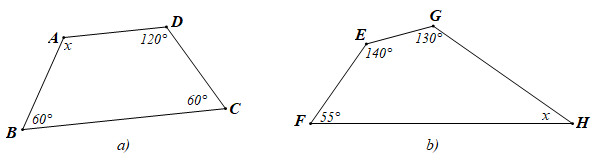Với giải bài tập Toán 8 Bài 2: Tứ giác sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 Bài 2.

Giải Toán 8 Chân trời sáng tạo Bài 2: Tứ giác

Giải Toán 8 trang 63

Khởi động trang 63 Toán 8 Tập 1 Chân trời sáng tạo

Giải Toán 8 Bài 2: Tứ giác - Chân trời sáng tạo

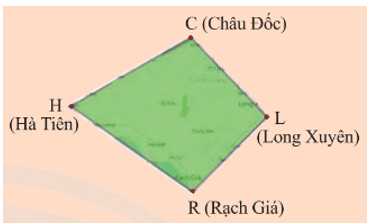
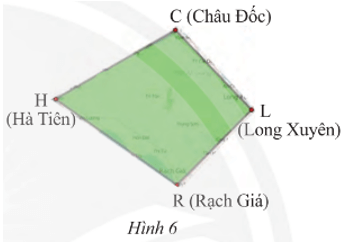
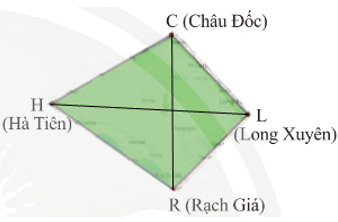
Khởi động trang 63 Toán 8 Tập 1: Hình màu xanh bên được trích ra từ bản đồ được gọi là Tứ giác Long Xuyên. Em hãy cho biết:

‒ Hình này được tạo bởi mấy đoạn thẳng?

‒ Các đoạn thẳng này nối các địa điểm nào?

Lời giải:

‒ Hình trên được tạo bởi 4 đoạn thẳng (CH, HR, RL, LC).

‒ Các đoạn thẳng này nối các địa điểm C (Châu Đốc), H (Hà Tiên), Q (Rạch Giá), L (Long Xuyên).

Lời giải bài tập Toán 8 Bài 2: Tứ giác hay, chi tiết khác:

Khám phá 1 trang 63 Toán 8 Tập 1 Chân trời sáng tạo

Giải Toán 8 Bài 2: Tứ giác - Chân trời sáng tạo

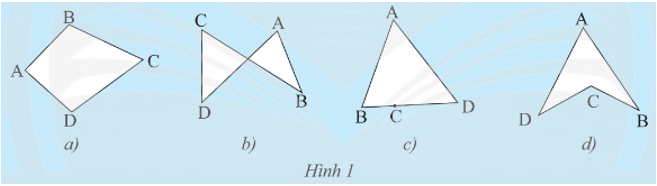
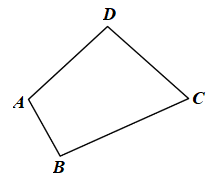
Khám phá 1 trang 63 Toán 8 Tập 1: Trong các hình tạo bởi bốn đoạn thẳng AB, BC, CD và DA sau đây, hình nào không có hai đoạn thẳng cùng nằm trên một đường thẳng?

Lời giải:

Trong các hình tạo bởi bốn đoạn thẳng AB, BC, CD và DA ở Hình 1, hình a), b), d) không có hai đoạn thẳng cùng nằm trên một đường thẳng.

Lời giải bài tập Toán 8 Bài 2: Tứ giác hay, chi tiết khác:

Khám phá 2 trang 64 Toán 8 Tập 1 Chân trời sáng tạo

Giải Toán 8 Bài 2: Tứ giác - Chân trời sáng tạo

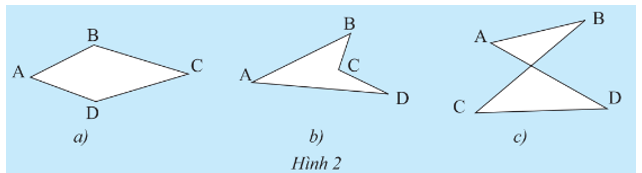
Khám phá 2 trang 64 Toán 8 Tập 1: Vẽ các đường thẳng lần lượt chứa mỗi cạnh của các tứ giác sau đây và nêu nhận xét của em về vị trí của các cạnh còn lại của tứ giác đối với mỗi đường thẳng đã vẽ.

Lời giải:

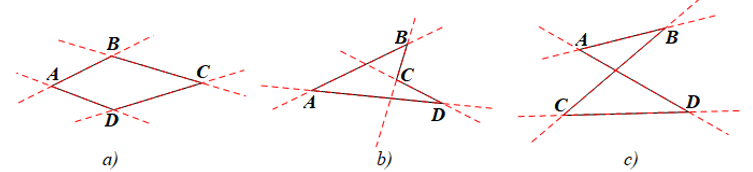
Ta vẽ các đường thẳng lần lượt chứa mỗi cạnh của các tứ giác như hình vẽ dưới đây:

Nhận xét:

• Hình a): các cạnh còn lại của tứ giác luôn nằm trong cùng một mặt phẳng được phân chia bởi đường thẳng chứa bất kì cạnh nào của tứ giác.

• Hình b): các cạnh còn lại của tứ giác không nằm trong cùng một mặt phẳng được phân chia bởi đường thẳng chứa cạnh BC (hoặc CD) của tứ giác.

• Hình c): các cạnh còn lại của tứ giác không nằm trong cùng một mặt phẳng được phân chia bởi đường thẳng chứa cạnh BC (hoặc AD) của tứ giác.

Lời giải bài tập Toán 8 Bài 2: Tứ giác hay, chi tiết khác:

Thực hành 1 trang 65 Toán 8 Tập 1 Chân trời sáng tạo

Giải Toán 8 Bài 2: Tứ giác - Chân trời sáng tạo

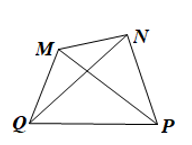
Thực hành 1 trang 65 Toán 8 Tập 1: Vẽ tứ giác MNPQ và tìm:

‒ Hai đỉnh đối nhau;

‒ Hai đường chéo;

‒ Hai cạnh đối nhau.

Lời giải:

Trong tứ giác MNPQ có:

‒ Hai đỉnh đối nhau: M và P; N và Q;

‒ Hai đường chéo: MP và NQ;

‒ Hai cạnh đối nhau: MN và PQ; MQ và NP.

Lời giải bài tập Toán 8 Bài 2: Tứ giác hay, chi tiết khác:

Vận dụng 1 trang 65 Toán 8 Tập 1 Chân trời sáng tạo

Giải Toán 8 Bài 2: Tứ giác - Chân trời sáng tạo

Vận dụng 1 trang 65 Toán 8 Tập 1: Tìm các đỉnh, cạnh và đường chéo của tứ giác Long Xuyên CHRL (Hình 6).

Lời giải:

Trong tứ giác Long Xuyên CHRL có:

• Các đỉnh: C, H, R, L;

• Các cạnh: CH, HR, RL, LC;

• Các đường chéo: CR và HL.

Lời giải bài tập Toán 8 Bài 2: Tứ giác hay, chi tiết khác:

Khám phá 3 trang 65 Toán 8 Tập 1 Chân trời sáng tạo

Giải Toán 8 Bài 2: Tứ giác - Chân trời sáng tạo

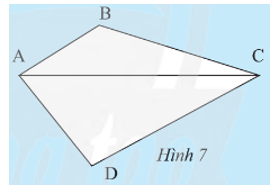
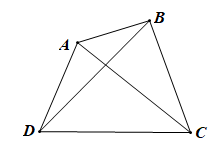
Khám phá 3 trang 65 Toán 8 Tập 1: Đường chéo AC chia tứ giác ABCD thành hai tam giác ACB và ACD (Hình 7). Tính tổng các góc của tam giác ACB và tam giác ACD. Từ đó, ta có nhận xét gì về tổng các góc của tứ giác ABCD?

Lời giải:

• Xét DACB có: $\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180°$ (định lí tổng ba góc trong một tam giác).

Xét DACD có: $\widehat{CAD}+\widehat{ACD}+\widehat{ADC}=180°$ (định lí tổng ba góc trong một tam giác).

Do đó $\widehat{BAC}+\widehat{ABC}+\widehat{ACB}+\widehat{CAD}+\widehat{ACD}+\widehat{ADC}=180°+180°=360°$.

Vậy tổng các góc của tam giác ACB và tam giác ACD bằng 360°.

• Ta có: $\widehat{BAC}+\widehat{ABC}+\widehat{ACB}+\widehat{CAD}+\widehat{ACD}+\widehat{ADC}=360°$

Suy ra $\left(\widehat{BAC}+\widehat{CAD}\right)+\widehat{ABC}+\left(\widehat{ACB}+\widehat{ACD}\right)+\widehat{ADC}=360°$

Hay $\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360°$.

Vậy tổng các góc của tứ giác ABCD bằng 360°.

Lời giải bài tập Toán 8 Bài 2: Tứ giác hay, chi tiết khác:

Thực hành 2 trang 66 Toán 8 Tập 1 Chân trời sáng tạo

Giải Toán 8 Bài 2: Tứ giác - Chân trời sáng tạo

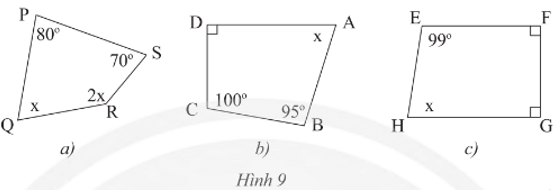
Thực hành 2 trang 66 Toán 8 Tập 1: Tìm x trong mỗi tứ giác sau:

Lời giải:

• Hình 9a):

Xét tứ giác PQRS có: 80° + 70° + 2x + x = 360° (định lí tổng các góc của một tứ giác)

Suy ra 3x = 360° – (80° + 70°) = 210°

Do đó x = 70°.

• Hình 9b):

Xét tứ giác ABCD có: x + 95° + 100° + 90° = 360° (định lí tổng các góc của một tứ giác)

Suy ra x = 360° – (95° + 100° + 90°) = 75°.

• Hình 9c):

Xét tứ giác EFGH có: 99° + 90° + 90° + x = 360° (định lí tổng các góc của một tứ giác)

Suy ra x = 360° – (99° + 90° + 90°) = 81°.

Lời giải bài tập Toán 8 Bài 2: Tứ giác hay, chi tiết khác:

Vận dụng 2 trang 66 Toán 8 Tập 1 Chân trời sáng tạo

Giải Toán 8 Bài 2: Tứ giác - Chân trời sáng tạo

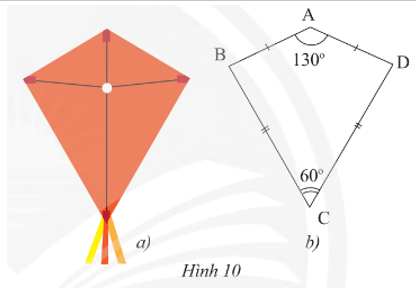
Vận dụng 2 trang 66 Toán 8 Tập 1: Phần thân của cái diều ở Hình 10a được vẽ lại như Hình 10b. Tìm số đo các góc chưa biết trong hình.

Lời giải:

Xét DABC và DADC có:

AC là cạnh chung; AB = AD; BC = DC (giả thiết).

Do đó DABC = DADC (c.c.c).

Suy ra $\widehat{B}=\widehat{D}$ (hai góc tương ứng).

Xét tứ giác ABCD có: $\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360°$ (định lí tổng các góc của một tứ giác)

Suy ra $130°+\widehat{B}+60°+\widehat{B}=360°$

Hay $2\widehat{B}=360°-\left(130°+60°\right)=170°$.

Do đó $\widehat{B}=85°$.

Vậy $\widehat{B}=\widehat{D}=85°$.

Lời giải bài tập Toán 8 Bài 2: Tứ giác hay, chi tiết khác:

Bài 1 trang 66 Toán 8 Tập 1 Chân trời sáng tạo

Giải Toán 8 Bài 2: Tứ giác - Chân trời sáng tạo

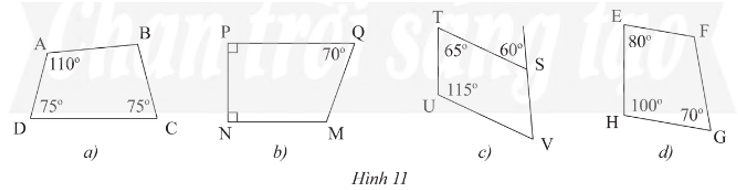
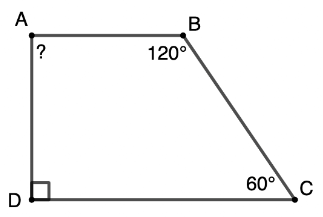
Bài 1 trang 66 Toán 8 Tập 1: Tìm số đo các góc chưa biết của các tứ giác trong Hình 11.

Lời giải:

• Hình 11a):

Xét tứ giác ABCD có: $\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360°$ (định lí tổng các góc của một tứ giác)

Suy ra $\widehat{B}=360°-\left(\widehat{A}+\widehat{C}+\widehat{D}\right)$

Hay $\widehat{B}=360°-\left(110°+75°+75°\right)=100°$.

• Hình 11b):

Xét tứ giác MNPQ có: $\widehat{M}+\widehat{N}+\widehat{P}+\widehat{Q}=360°$ (định lí tổng các góc của một tứ giác)

Suy ra $\widehat{M}=360°-\left(\widehat{N}+\widehat{P}+\widehat{Q}\right)$

Hay $\widehat{M}=360°-\left(90°+90°+70°\right)=110°$.

• Hình 11c):

Ta có $\widehat{TSV}=180°-60°=120°$ (do $\widehat{TSV}$ kề bù với góc có số đo bằng 60°)

Xét tứ giác STUV có: $\widehat{TSV}+\widehat{T}+\widehat{U}+\widehat{V}=360°$ (định lí tổng các góc của một tứ giác)

Suy ra $\widehat{V}=360°-\left(\widehat{TSV}+\widehat{T}+\widehat{U}\right)$

Hay $\widehat{V}=360°-\left(120°+65°+115°\right)=60°$.

• Hình 11d):

Xét tứ giác EFGH có: $\widehat{E}+\widehat{F}+\widehat{G}+\widehat{H}=360°$ (định lí tổng các góc của một tứ giác)

Suy ra $\widehat{F}=360°-\left(\widehat{E}+\widehat{G}+\widehat{H}\right)$

Hay $\widehat{F}=360°-\left(80°+70°+100°\right)=110°$.

Lời giải bài tập Toán 8 Bài 2: Tứ giác hay, chi tiết khác:

Bài 2 trang 66 Toán 8 Tập 1 Chân trời sáng tạo

Giải Toán 8 Bài 2: Tứ giác - Chân trời sáng tạo

Bài 2 trang 66 Toán 8 Tập 1: Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó.

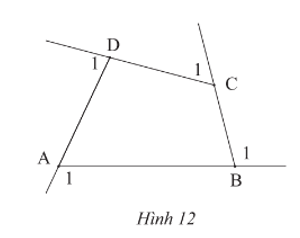
Hãy tính tổng số đo bốn góc ngoài  của tứ giác ABCD ở Hình 12.

Lời giải:

Xét tứ giác ABCD có: ${\widehat{A}}_2+{\widehat{B}}_2+{\widehat{C}}_2+{\widehat{D}}_2=360°$ (định lí tổng các góc của một tứ giác)

Mặt khác: ${\widehat{A}}_1+{\widehat{A}}_2=180°$ (hai góc kề bù)

Tương tự: ${\widehat{B}}_1+{\widehat{B}}_2=180°; {\widehat{C}}_1+{\widehat{C}}_2=180°; {\widehat{D}}_1+{\widehat{D}}_2=180°$

Suy ra

$\left({\widehat{A}}_1+{\widehat{A}}_2\right)+\left({\widehat{B}}_1+{\widehat{B}}_2\right)+\left({\widehat{C}}_1+{\widehat{C}}_2\right)+\left({\widehat{D}}_1+{\widehat{D}}_2\right)=180°+180°+180°+180°$

Hay ${\widehat{A}}_1+{\widehat{B}}_1+{\widehat{C}}_1+{\widehat{D}}_1+\left({\widehat{A}}_2+{\widehat{B}}_2+{\widehat{C}}_2+{\widehat{D}}_2\right)=720°$

Do đó ${\widehat{A}}_1+{\widehat{B}}_1+{\widehat{C}}_1+{\widehat{D}}_1+360°=720°$

Nên ${\widehat{A}}_1+{\widehat{B}}_1+{\widehat{C}}_1+{\widehat{D}}_1=720°-360°=360°$.

Vậy tổng số đo bốn góc ngoài ${\widehat{A}}_1,{\widehat{B}}_1,{\widehat{C}}_1,{\widehat{D}}_1$ của tứ giác ABCD bằng 360°.

Lời giải bài tập Toán 8 Bài 2: Tứ giác hay, chi tiết khác:

Bài 3 trang 67 Toán 8 Tập 1 Chân trời sáng tạo

Giải Toán 8 Bài 2: Tứ giác - Chân trời sáng tạo

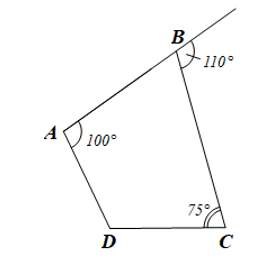
Bài 3 trang 67 Toán 8 Tập 1: Tứ giác ABCD có $\widehat{A}=100°$, góc ngoài tại đỉnh B bằng 110°, $\widehat{C}=75°$. Tính số đo góc D

Lời giải:

Do góc ngoài tại đỉnh B có số đo bằng 110° nên $\widehat{ABC}=180°-110°=70°$.

Xét tứ giác ABCD có: $\widehat{A}+\widehat{ABC}+\widehat{C}+\widehat{D}=360°$ (định lí tổng các góc của một tứ giác)

Suy ra $\widehat{D}=360°-\left(\widehat{A}+\widehat{ABC}+\widehat{C}\right)$

Do đó $\widehat{D}=360°-\left(100°+70°+75°\right)=115°$.

Lời giải bài tập Toán 8 Bài 2: Tứ giác hay, chi tiết khác:

Bài 4 trang 67 Toán 8 Tập 1 Chân trời sáng tạo

Giải Toán 8 Bài 2: Tứ giác - Chân trời sáng tạo

Bài 4 trang 67 Toán 8 Tập 1: Tứ giác ABCD có góc ngoài tại đỉnh A bằng 65°, góc ngoài tại đỉnh B bằng 100°, góc ngoài tại đỉnh C bằng 60°. Tính số đo góc ngoài tại đỉnh D.

Lời giải:

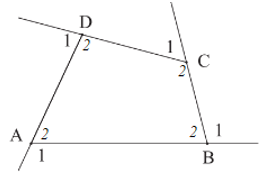
Gọi ${\widehat{A}}_1,{\widehat{B}}_1,{\widehat{C}}_1,{\widehat{D}}_1$ lần lượt là các góc ngoài tại đỉnh A, đỉnh B, đỉnh C, đỉnh D (hình vẽ).

Áp dụng kết quả của Bài tập 2, trang 66 Sách giáo khoa Toán 8, Tập một cho tứ giác ABCD ta có: ${\widehat{A}}_1+{\widehat{B}}_1+{\widehat{C}}_1+{\widehat{D}}_1=360°$

Suy ra${\widehat{D}}_1=360°-\left({\widehat{A}}_1+{\widehat{B}}_1+{\widehat{C}}_1\right)$

Do đó ${\widehat{D}}_1=360°-\left(65°+100°+60°\right)=135°$

Vậy góc ngoài tại đỉnh D có số đo bằng 135°.

Lời giải bài tập Toán 8 Bài 2: Tứ giác hay, chi tiết khác:

Bài 5 trang 67 Toán 8 Tập 1 Chân trời sáng tạo

Giải Toán 8 Bài 2: Tứ giác - Chân trời sáng tạo

Bài 5 trang 67 Toán 8 Tập 1: Tứ giác ABCD có số đo $\widehat{A}=x,\widehat{B}=2x,\widehat{C}=3x,\widehat{D}=4x$. Tính số đo các góc của tứ giác đó

Lời giải:

Xét tứ giác ABCD có: $\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360°$ (định lí tổng các góc của một tứ giác)

Suy ra x + 2x + 3x + 4x = 360°

Hay 10x = 360°

Do đó x = 36°.

Khi đó: $\widehat{A}=36°;\widehat{B}=2.36°=72°;\widehat{C}=3.36°=108°;\widehat{D}=4.36°=144°$.

Vậy $\widehat{A}=36°;\widehat{B}=72°;\widehat{C}=108°;\widehat{D}=144°$.

Lời giải bài tập Toán 8 Bài 2: Tứ giác hay, chi tiết khác:

Bài 6 trang 67 Toán 8 Tập 1 Chân trời sáng tạo

Giải Toán 8 Bài 2: Tứ giác - Chân trời sáng tạo

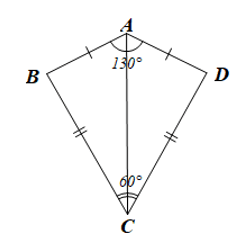
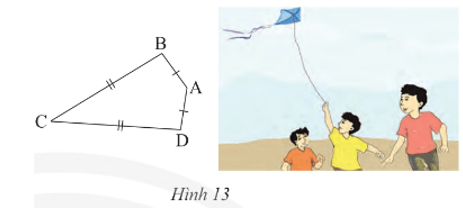
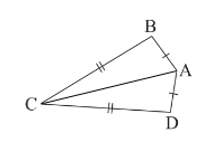
Bài 6 trang 67 Toán 8 Tập 1: Ta gọi tứ giác ABCD với AB = AD, CB = CD (Hình 13) là hình “cái diều”.

a) Chứng minh rằng AC là đường trung trực của BD.

b) Cho biết $\widehat{B}=95°$, $\widehat{C}=35°$. Tính $\widehat{A}$ và $\widehat{D}$.

Lời giải:

a) Vì AB = AD nên A nằm trên đường trung trực của đoạn thẳng BD.

Vì CB = CD nên C nằm trên đường trung trực của đoạn thẳng BD.

Do đó AC là đường trung trực của đoạn thẳng BD.

b) Xét DABC và DADC có:

AC là cạnh chung; AB = AD; BC = DC (giả thiết).

Do đó DABC = DADC (c.c.c).

Suy ra $\widehat{B}=\widehat{D}$ (hai góc tương ứng).

Mà $\widehat{B}=95°$ nên $\widehat{D}=95°$.

Xét tứ giác ABCD có: $\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360°$ (định lí tổng các góc của một tứ giác)

Suy ra $\widehat{A}=360°-\left(\widehat{B}+\widehat{C}+\widehat{D}\right)$

Do đó $\widehat{A}=360°-\left(95°+35°+95°\right)=135°$.

Vậy $\widehat{A}=135°$ và $\widehat{D}=95°$.

Lời giải bài tập Toán 8 Bài 2: Tứ giác hay, chi tiết khác:

Bài 7 trang 67 Toán 8 Tập 1 Chân trời sáng tạo

Giải Toán 8 Bài 2: Tứ giác - Chân trời sáng tạo

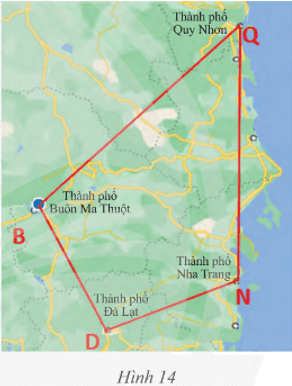
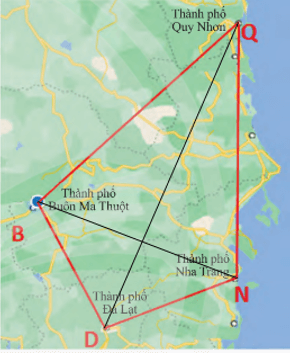
Bài 7 trang 67 Toán 8 Tập 1: Trên bản đồ, tứ giác BDNQ với các đỉnh là các thành phố Buôn Ma Thuột, Đà Lạt, Nha Trang, Quy Nhơn.

a) Tìm các cạnh kề và cạnh đối của cạnh BD.

b) Tìm các đường chéo của tứ giác.

Lời giải:

a) Tứ giác BDNQ có:

• Các cạnh kề: BD và BQ; DB và DN; ND và NQ; QN và QB;

• Các cạnh đối: BD và NQ; DN và BQ.

b) Tứ giác BDNQ có các đường chéo BN và DQ.

Lời giải bài tập Toán 8 Bài 2: Tứ giác hay, chi tiết khác:

SBT Toán 8 Chân trời sáng tạo Bài 2: Tứ giác

Với giải sách bài tập Toán 8 Bài 2: Tứ giác sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 8 dễ dàng làm bài tập trong SBT Toán 8 Bài 2.

Giải SBT Toán 8 Chân trời sáng tạo Bài 2: Tứ giác

Tứ giác (Lý thuyết Toán lớp 8) - Chân trời sáng tạo

Với tóm tắt lý thuyết Toán 8 Bài 2: Tứ giác sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 8 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Tứ giác (Lý thuyết Toán lớp 8) - Chân trời sáng tạo

Lý thuyết Tứ giác

1. Tứ giác

1.1. Tứ giác

Định nghĩa tứ giác:

Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD và DA, trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.

Đỉnh và cạnh của tứ giác:

– Tứ giác ABCD còn được gọi là tứ giác ADCB, BADC, BCDA, CBAD, CDAB, DCBA, DABC.

– Các điểm A, B, C, D gọi là các đỉnh.

– Các đoạn thẳng AB, BC, CD, DA gọi là các cạnh.

2.2. Tứ giác lồi

Định nghĩa tứ giác lồi:

Tứ giác lồi là tứ giác có luôn nằm trong cùng một phần mặt phẳng được phân chia bởi đường thẳng chứa bất kì cạnh nào của tứ giác.

Chú ý: Từ nay, khi nói đến tứ giác mà không chú thích gì thêm, ta hiểu đó là tứ giác lồi.

Ví dụ 1. Hình nào trong các hình sau là tứ giác, đó có phải tứ giác lồi không?

Hướng dẫn giải

–Theo định nghĩa tứ giác, trong các hình trên chỉ có JKLM là tứ giác.

–Theo định nghĩa tứ giác lồi, nếu kẻ một đường thẳng bất kì đi qua hai cạnh của tứ giác JKLM thì đều đảm bảo hai đỉnh thuộc một cạnh còn lại luôn nằm về một phía của đường thẳng đó. Vì vậy tứ giác JKLM là tứ giác lồi.

Cạnh, góc, đường chéo của tứ giác

Trong một tứ giác:

a) Hai cạnh kề nhau là hai cạnh có chung một đỉnh.

b) Hai cạnh kề nhau tạo thành một góc của tứ giác.

c) Hai cạnh đối nhau là hai cạnh không có chung đỉnh nào.

d) Hai đỉnh đối nhau là hai đỉnh không cùng nằm trên một cạnh.

e) Đường chéo của đoạn thẳng nối hai đỉnh với nhau.

Ví dụ 2. Cho hình vẽ dưới đây:

Trong tứ giác ABCD, có:

• BA và BC; AB và AD; CB và CD; DA và DC là các cặp cạnh kề nhau.

• các góc $\widehat{DAB},\widehat{ABC},\widehat{BCD},\widehat{CDA}$ . Các cặp góc $\widehat{DAB}$ và $\widehat{BCD}$ ; $\widehat{ABC}$ và $\widehat{CDA}$ được gọi là cặp góc đối.

• AB và DC; AD và BC là các cặp cạnh đối nhau.

• Đỉnh A và C; đỉnh B và D là các cặp đỉnh đối nhau.

• AC và BD là hai đường chéo.

2. Tổng các góc của một tứ giác

Định lí:Tổng số đo các góc của một tứ giác bằng 360°.

Ví dụ 3. Tính trong tứ giác ABCD ở hình vẽ sau:

Hướng dẫn giải

Theo định lí tổng các góc của một tứ giác, tứ giác ABCD có: $\hat{A}+\hat{B}+\hat{C}+\hat{D}={360}^o$

Do đó $\hat{A}={360}^o-\left(\hat{B}+\hat{C}+\hat{D}\right)$

$\hat{A}={360}^o-\left({120}^o+{60}^o+{90}^o\right)={360}^o-{270}^o={90}^o$

Vậy $\hat{A}={90}^o$ .

Bài tập Tứ giác

Bài 1. Cho bốn điểm E, F, G, H (hình vẽ).

Vẽ một tứ giác có các đỉnh là bốn điểm đã cho và tìm các yếu tố sau:

a) cạnh kề, cạnh đối của cạnh GH.

b) góc đối của $\widehat{EFG}$ .

c) hai đường chéo của tứ giác.

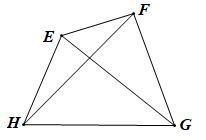
Hướng dẫn giải

a) Cạnh kề của cạnh GH là cạnh GF; cạnh đối của cạnh GH là cạnh EF.

b) Góc đối của $\widehat{EFG}$ là $\widehat{EHG}$ .

c) Hai đường chéo của tứ giác là EG và FH.

Bài 2. Tính x trong mỗi hình sau:

Hướng dẫn giải

a) Theo định lí tổng các góc của một tứ giác, trong tứ giác ABCD có:

$\hat{A}+\hat{B}+\hat{C}+\hat{D}={360}^o$

Suy ra $x=\hat{A}={360}^o-\left(\hat{B}+\hat{C}+\hat{D}\right)$

$x={360}^o-\left({60}^o+{60}^o+{120}^o\right)={360}^o-{240}^o={120}^o$

Vậy $x={120}^o$ .

b) Theo định lí tổng các góc của một tứ giác, trong tứ giác EGHF có: $\hat{E}+\hat{G}+\hat{H}+\hat{F}={360}^o$

Suy ra $x=\hat{H}={360}^o-\left(\hat{E}+\hat{G}+\hat{F}\right)$

$x={360}^o-\left({140}^o+{130}^o+{55}^o\right)={360}^o-{325}^o={35}^o$

Vậy $x={35}^o$

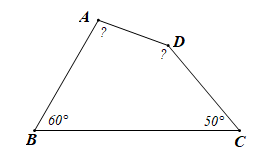
Bài3.Tứ giác ABCD có $\hat{C}=50°$ ; $\hat{B}=60°$ ; $\hat{A}-\hat{B}=40°$ . Tính số đo các góc A và D.

Hướng dẫn giải

Theo giả thiết: $\hat{A}-\hat{B}={40}^o$nên $\hat{A}={40}^o+\hat{B}={40}^o+{60}^o={100}^o$

Theo định lí tổng các góc của một tứ giác, trong tứ giác ABCD có:

$\hat{A}+\hat{B}+\hat{C}+\hat{D}={360}^o$

Suy ra $\hat{D}={360}^o-\left(\hat{B}+\hat{C}+\hat{A}\right)$

$\hat{D}={360}^o-\left({60}^o+{50}^o+{100}^o\right)={360}^o-{210}^o={150}^o$

Vậy $\hat{A}={100}^o;\hat{D}={150}^o$

Học tốt Tứ giác

Các bài học để học tốt Tứ giác Toán lớp 8 hay khác:

15 Bài tập Tứ giác (có đáp án) - Chân trời sáng tạo Trắc nghiệm Toán 8

Với 15 bài tập trắc nghiệm Tứ giác Toán lớp 8 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Chân trời sáng tạo sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 8.

15 Bài tập Tứ giác (có đáp án) - Chân trời sáng tạo Trắc nghiệm Toán 8

Nội dung đang được cập nhật ...

Xem thêm bài tập trắc nghiệm Toán lớp 8 Chân trời sáng tạo có đáp án hay khác: