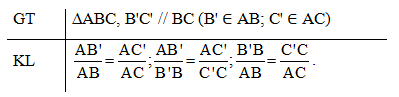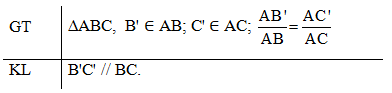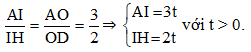Với giải bài tập Toán 8 Bài 15: Định lí Thalès trong tam giác sách Kết nối tri thức hay nhất, chi tiết giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 Bài 15.

Giải Toán 8 Kết nối tri thức Bài 15: Định lí Thalès trong tam giác

Video Giải Toán 8 Bài 15: Định lí Thalès trong tam giác - Cô Vũ Chuyên (Giáo viên VietJack)

Mở đầu trang 76 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 15: Định lí Thalès trong tam giác - Kết nối tri thức

Mở đầu trang 76 Toán 8 Tập 1: Cây cầu AB bắc qua một con sông có chiều rộng 300 m. Để đo khoảng cách giữa hai điểm C và D trên hai bờ con sông, người ta chọn một điểm E trên đường thẳng AB sao cho ba điểm E, C, D thẳng hàng. Trên mặt đất, người ta đo được AE = 400 m, EC = 500 m. Theo em, người ta tính khoảng cách giữa C và D như thế nào?

Lời giải:

Sau bài học này ta giải quyết được bài toán như sau:

Hai cạnh AC và BD thuộc hai bờ của con sông nên AC // BD, áp dụng định lí Thalès, ta có:

$\frac{AE}{AB}=\frac{CE}{CD}$ hay $\frac{400}{300}=\frac{500}{CD}$ .

Suy ra $CD=\frac{300.500}{400}=375$ (m).

Vậy khoảng cách giữa C và D bằng 375 m.

Lời giải bài tập Toán 8 Bài 15: Định lí Thalès trong tam giác hay, chi tiết khác:

HĐ1 trang 77 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 15: Định lí Thalès trong tam giác - Kết nối tri thức

HĐ1 trang 77 Toán 8 Tập 1: Cho Hình 4.2, em hãy thực hiện các hoạt động sau:

Hãy tìm độ dài của hai đoạn thẳng AB và CD nếu chọn đoạn MN làm đơn vị độ dài. Với các độ dài đó hãy tính tỉ số $\frac{AB}{CD}$.

Lời giải:

Chọn đoạn MN làm đơn vị độ dài thì MN = 1 (đvđd).

Khi đó, AB = 2 (đvđd); CD = 6 (đvđd).

Do đó $\frac{AB}{CD}=\frac{2}{6}=\frac{1}{3}$.

Vậy AB = 2 (đvđd); CD = 6 (đvđd); $\frac{AB}{CD}=\frac{1}{3}$.

Lời giải bài tập Toán 8 Bài 15: Định lí Thalès trong tam giác hay, chi tiết khác:

HĐ2 trang 77 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 15: Định lí Thalès trong tam giác - Kết nối tri thức

HĐ2 trang 77 Toán 8 Tập 1: Cho Hình 4.2, em hãy thực hiện các hoạt động sau:

Dùng thước thẳng, đo độ dài hai đoạn thẳng AB và CD (đơn vị: cm) rồi dùng kết quả vừa đo để tính tỉ số $\frac{AB}{CD}$.

Lời giải:

Đo độ dài các đoạn thẳng, ta được: AB = 3 cm; CD = 9 cm.

Khi đó $\frac{AB}{CD}=\frac{3}{9}=\frac{1}{3}$.

Lời giải bài tập Toán 8 Bài 15: Định lí Thalès trong tam giác hay, chi tiết khác:

HĐ3 trang 77 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 15: Định lí Thalès trong tam giác - Kết nối tri thức

HĐ3 trang 77 Toán 8 Tập 1: So sánh hai tỉ số tìm được trong hai hoạt động trên.

Lời giải:

Tỉ số $\frac{AB}{CD}$ tìm được ở Hoạt động 1 và Hoạt động 2 bằng nhau và đều bằng $\frac{1}{3}$.

Lời giải bài tập Toán 8 Bài 15: Định lí Thalès trong tam giác hay, chi tiết khác:

Luyện tập 1 trang 77 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 15: Định lí Thalès trong tam giác - Kết nối tri thức

Luyện tập 1 trang 77 Toán 8 Tập 1: Tìm tỉ số của các đoạn thẳng có độ dài như sau:

a) MN = 3 cm và PQ = 9 cm.

b) EF = 25 cm và HK = 10 dm.

Lời giải:

a) Tỉ số của các đoạn thẳng được tính như sau: $\frac{MN}{PQ}=\frac{3}{9}=\frac{1}{3};\frac{PQ}{MN}=\frac{9}{3}=\frac{3}{1}$.

Vậy $\frac{MN}{PQ}=\frac{1}{3};\frac{PQ}{MN}=\frac{3}{1}$.

b) Đổi 10 dm = 100 cm.

Tỉ số của các đoạn thẳng được tính như sau: $\frac{EF}{HK}=\frac{25}{100}=\frac{1}{4}$; $\frac{HK}{EF}=\frac{100}{25}=\frac{4}{1}$.

Vậy $\frac{EF}{HK}=\frac{1}{4};\frac{HK}{EF}=\frac{4}{1}$.

Lời giải bài tập Toán 8 Bài 15: Định lí Thalès trong tam giác hay, chi tiết khác:

Luyện tập 2 trang 78 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 15: Định lí Thalès trong tam giác - Kết nối tri thức

Luyện tập 2 trang 78 Toán 8 Tập 1: Cho tam giác ABC và một điểm B’ nằm trên cạnh AB. Qua điểm B’, ta vẽ một đường thẳng song song với BC, cắt AC tại C’ (H.4.4).

Dựa vào hình vẽ, hãy tính và so sánh các tỉ số sau và viết các tỉ lệ thức:

a) $\frac{AB\text{'}}{AB}$ và $\frac{AC\text{'}}{AC}$ .

b) $\frac{AB\text{'}}{B\text{'}B}$  và $\frac{AC\text{'}}{C\text{'}C}$ .

c) $\frac{B\text{'}B}{AB}$  và $\frac{C\text{'}C}{AC}$.

Lời giải:

a) Từ hình vẽ ta thấy: $\frac{AB\text{'}}{AB}=\frac{4}{6}=\frac{2}{3};\frac{AC\text{'}}{AC}=\frac{4}{6}=\frac{2}{3}$.

Do đó, $\frac{AB\text{'}}{AB}=\frac{AC\text{'}}{AC}$.

b) Từ hình vẽ ta thấy: $\frac{AB\text{'}}{B\text{'}B}=\frac{4}{2}=\frac{2}{1};\frac{AC\text{'}}{C\text{'}C}=\frac{4}{2}=\frac{2}{1}$.

Vậy $\frac{AB\text{'}}{B\text{'}B}=\frac{AC\text{'}}{C\text{'}C}$.

c) Từ hình vẽ ta thấy: $\frac{B^{\text{'}}B}{AB}=\frac{2}{6}=\frac{1}{3}$; $\frac{C^{\text{'}}C}{AC}=\frac{2}{6}=\frac{1}{3}$.

Do đó $\frac{B\text{'}B}{AB}=\frac{C\text{'}C}{AC}$.

Lời giải bài tập Toán 8 Bài 15: Định lí Thalès trong tam giác hay, chi tiết khác:

Luyện tập 3 trang 79 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 15: Định lí Thalès trong tam giác - Kết nối tri thức

Luyện tập 3 trang 79 Toán 8 Tập 1: Tìm các độ dài x, y trong Hình 4.6.

Lời giải:

a) Áp dụng định lí Thalès vào ∆ABC, ta có:

$\frac{AM}{BM}=\frac{AN}{CN}$ hay $\frac{\mathrm{6,5}}{x}=\frac{4}{2}$ .

Suy ra $x=\frac{\mathrm{6,5}.2}{4}=\mathrm{3,25}$  (đvđd).

Vậy x = 3,25 (đvđd).

b) Ta có: PQ = PF + QF = 5 + 3,5 = 8,5 (đvđd).

Áp dụng định lí Thalès vào ∆PHQ, ta có:

$\frac{PE}{PH}=\frac{PF}{PQ}$ hay $\frac{4}{y}=\frac{5}{\mathrm{8,5}}$ .

Suy ra $y=\frac{4.\mathrm{8,5}}{5}=\mathrm{6,8}$  (đvđd).

Vậy y = 6,8 (đvđd).

Lời giải bài tập Toán 8 Bài 15: Định lí Thalès trong tam giác hay, chi tiết khác:

HĐ4 trang 79 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 15: Định lí Thalès trong tam giác - Kết nối tri thức

HĐ4 trang 79 Toán 8 Tập 1: Cho ∆ABC có AB = 6 cm, AC = 9 cm. Trên cạnh AB lấy điểm B’, trên cạnh AC lấy điểm C’ sao cho AB’ = 4 cm, AC’ = 6 cm (H.4.7).

• So sánh các tỉ số $\frac{AB\text{'}}{AB}$ và $\frac{AC\text{'}}{AC}$ .

• Vẽ đường thẳng a đi qua B’ và song song với BC, đường thẳng qua a cắt AC tại điểm C’’. Tính độ dài đoạn thẳng AC’’.

• Nhận xét gì về hai điểm C’, C’’ và hai đường thẳng B’C’, BC?

Lời giải:

• Ta có $\frac{AB\text{'}}{AB}=\frac{4}{6}=\frac{2}{3}$; $\frac{AC\text{'}}{AC}=\frac{6}{9}=\frac{2}{3}$ .

Do đó $\frac{AB\text{'}}{AB}=\frac{AC\text{'}}{AC}$ .

• Đường thẳng a đi qua B’ và song song với BC, đường thẳng qua a cắt AC tại điểm C’’ nên B’C’’ // BC.

Áp dụng định lí Thalès vào ∆ABC, ta có:

$\frac{AB\text{'}}{AB}=\frac{AC\text{'}\text{'}}{AC}$ hay $\frac{4}{6}=\frac{AC\text{'}\text{'}}{9}$ .

Suy ra $AC\text{'}\text{'}=\frac{4.9}{6}=6$(cm).

Vậy AC’’ = 6 cm.

• Trên cạnh AC lấy điểm C’ sao cho AC’ = 6 cm.

Đường thẳng a đi qua B’ và song song với BC, đường thẳng qua a cắt AC tại điểm C’’ nên điểm C’’ nằm trên cạnh AC sao cho AC’’ = 6 cm.

Do đó, hai điểm C’, C’’ trùng nhau.

Vì hai điểm C’, C’’ trùng nhau mà B’C’’ // BC nên B’C’ // BC.

Lời giải bài tập Toán 8 Bài 15: Định lí Thalès trong tam giác hay, chi tiết khác:

Vận dụng trang 80 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 15: Định lí Thalès trong tam giác - Kết nối tri thức

Vận dụng trang 80 Toán 8 Tập 1: Em hãy trả lời câu hỏi trong tình huống mở đầu.

Cây cầu AB bắc qua một con sông có chiều rộng 300 m. Để đo khoảng cách giữa hai điểm C và D trên hai bờ con sông, người ta chọn một điểm E trên đường thẳng AB sao cho ba điểm E, C, D thẳng hàng. Trên mặt đất, người ta đo được AE = 400 m, EC = 500 m. Theo em, người ta tính khoảng cách giữa C và D như thế nào?

Lời giải:

Hai cạnh AC và BD thuộc hai bờ của con sông nên AC // BD, áp dụng định lí Thalès, ta có:

$\frac{AE}{AB}=\frac{CE}{CD}$ hay $\frac{400}{300}=\frac{500}{CD}$.

Suy ra $CD=\frac{300.500}{400}=375$ (m).

Vậy khoảng cách giữa C và D bằng 375 m.

Lời giải bài tập Toán 8 Bài 15: Định lí Thalès trong tam giác hay, chi tiết khác:

Bài 4.1 trang 80 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 15: Định lí Thalès trong tam giác - Kết nối tri thức

Bài 4.1 trang 80 Toán 8 Tập 1: Tìm độ dài x, y trong Hình 4.9 (làm tròn kết quả đến chữ số thập phân thứ nhất).

Lời giải:

• Hình 4.9a)

Vì HK // QE nên áp dụng định lí Thalès, ta có:

$\frac{PH}{QH}=\frac{PK}{KE}$ hay $\frac{6}{4}=\frac{8}{x}$ .

Suy ra $x=\frac{8.4}{6}=\frac{16}{3}\approx \mathrm{5,3}$  (đvđd).

• Hình 4.9b)

Vì $\widehat{AMN}=\widehat{ABC}$ mà $\widehat{AMN}$ và $\widehat{ABC}$ là hai góc đồng vị nên MN // BC.

Ta có AB = AM + BM = y + 6,5.

Áp dụng định lí Thalès, ta có: $\frac{AM}{AB}=\frac{AN}{AC}$  hay $\frac{y}{y+\mathrm{6,5}}=\frac{8}{11}$ .

Suy ra 11y = 8(y + 6,5)

11y = 8y + 52

11y – 8y = 52

3y = 52

$y=\frac{52}{3}\approx \mathrm{17,3}$(đvđd)

Vậy x ≈ 5,3 (đvđd); y ≈ 17,3 (đvđd).

Lời giải bài tập Toán 8 Bài 15: Định lí Thalès trong tam giác hay, chi tiết khác:

Bài 4.2 trang 80 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 15: Định lí Thalès trong tam giác - Kết nối tri thức

Bài 4.2 trang 80 Toán 8 Tập 1: Tìm các cặp đường thẳng song song trong Hình 4.10 và giải thích tại sao chúng song song với nhau.

Lời giải:

• Hình 4.10a)

Ta có $\frac{EM}{EN}=\frac{2}{3};\frac{MF}{PF}=\frac{3}{\mathrm{4,5}}=\frac{2}{3}$  nên $\frac{EM}{EN}=\frac{MF}{PF}$ .

Vì $\frac{EM}{EN}=\frac{MF}{PF}$ , E ∈ MN, F ∈ MP nên theo định lí Thalès đảo ta suy ra EF // NP.

• Hình 4.10b)

* Ta có: $\frac{HF}{KF}=\frac{14}{12}=\frac{7}{6};\frac{HM}{MQ}=\frac{15}{10}=\frac{3}{2}$ .

Vì $\frac{HF}{KF}\ne \frac{HM}{MQ}$ nên MF không song song với KQ.

* Ta có: $\frac{MQ}{MH}=\frac{10}{15}=\frac{2}{3};\frac{EQ}{EK}=\frac{12}{18}=\frac{2}{3}$ .

Vì $\frac{MQ}{MH}=\frac{EQ}{EK}$ ; E ∈ KQ; M ∈ HQ HQ nên theo định lí Thalès đảo ta suy ra ME // HK.

Lời giải bài tập Toán 8 Bài 15: Định lí Thalès trong tam giác hay, chi tiết khác:

Bài 4.3 trang 80 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 15: Định lí Thalès trong tam giác - Kết nối tri thức

Bài 4.3 trang 80 Toán 8 Tập 1: Cho ∆ABC, từ điểm D trên cạnh BC, kẻ đường thẳng song song với AB cắt AC tại F và kẻ đường thẳng song song với AC cắt AB tại E.

Chứng minh rằng: $\frac{AE}{AB}+\frac{AF}{AC}=1$.

Lời giải:

Áp dụng định lí Thalès, ta có:

• Vì DE // AC nên $\frac{AE}{AB}=\frac{CD}{BC}$;

• Vì DF // AC nên $\frac{AF}{AC}=\frac{BD}{BC}$.

Khi đó, $\frac{AE}{AB}+\frac{AF}{AC}$ = $\frac{CD}{BC}+\frac{BD}{BC}$ = $\frac{BC}{BC}$ = 1

Lời giải bài tập Toán 8 Bài 15: Định lí Thalès trong tam giác hay, chi tiết khác:

Bài 4.4 trang 80 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 15: Định lí Thalès trong tam giác - Kết nối tri thức

Bài 4.4 trang 80 Toán 8 Tập 1: Cho ∆ABC có trọng tâm G. Vẽ đường thẳng d qua G và song song với AB, d cắt BC tại điểm M. Chứng minh rằng $BM=\frac{1}{3}BC$

Lời giải:

Lấy D là trung điểm của cạnh BC.

Khi đó, AD là đường trung tuyến của tam giác ABC.

Vì G là trọng tâm của tam giác ABC nên điểm G nằm trên cạnh AD.

Ta có $\frac{AG}{AD}=\frac{2}{3}$ hay $AG=\frac{2}{3}AD$.

Vì MG // AB, theo định lí Thalès, ta suy ra: $\frac{AG}{AD}=\frac{BM}{BD}=\frac{2}{3}$.

Ta có BD = CD (vì D là trung điểm của cạnh BC) nên $\frac{BM}{BC}=\frac{BM}{2BD}=\frac{2}{2.3}=\frac{1}{3}$.

Do đó $BM=\frac{1}{3}BC$ (đpcm).

Lời giải bài tập Toán 8 Bài 15: Định lí Thalès trong tam giác hay, chi tiết khác:

Bài 4.5 trang 80 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 15: Định lí Thalès trong tam giác - Kết nối tri thức

Bài 4.5 trang 80 Toán 8 Tập 1: Để đo khoảng cách giữa hai vị trí B và E ở hai bên bờ sông, bác An chọn ba vị trí A, F, C cùng nằm ở một bên bờ sông sao cho ba điểm C, E, B thẳng hàng, ba điểm C, F, A thẳng hàng và AB // EF (H.4.11). Sau đó bác An đo được AF = 40 m, FC = 20 m, EC = 30 m. Hỏi khoảng cách giữa hai vị trí B và E bằng bao nhiêu?

Lời giải:

Theo đề bài, ba điểm C, E, B thẳng hàng, ba điểm C, F, A thẳng hàng và AB // EF, áp dụng định lí Thalès, ta có:

$\frac{EC}{BE}=\frac{CF}{AF}$ hay $\frac{30}{BE}=\frac{20}{40}$ .

Suy ra $BE=\frac{30.40}{20}=60$  (m).

Vậy khoảng cách giữa hai vị trí B và E bằng 60 m.

Lời giải bài tập Toán 8 Bài 15: Định lí Thalès trong tam giác hay, chi tiết khác:

SBT Toán 8 Kết nối tri thức Bài 15: Định lí Thalès trong tam giác

Với giải sách bài tập Toán 8 Bài 15: Định lí Thalès trong tam giác sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 8 dễ dàng làm bài tập trong SBT Toán 8 Bài 15.

Giải SBT Toán 8 Kết nối tri thức Bài 15: Định lí Thalès trong tam giác

Vở thực hành Toán 8 Bài 15: Định lí Thalès trong tam giác - Kết nối tri thức

Với giải vở thực hành Toán 8 Bài 15: Định lí Thalès trong tam giác sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 8 dễ dàng làm bài tập về nhà trong VTH Toán 8 Bài 15.

Giải vở thực hành Toán 8 Bài 15: Định lí Thalès trong tam giác - Kết nối tri thức

B – CÂU HỎI TRẮC NGHIỆM

Chọn phương án đúng trong mỗi câu sau:

Định lí Thalès trong tam giác (Lý thuyết Toán lớp 8) | Kết nối tri thức

Với tóm tắt lý thuyết Toán 8 Bài 15: Định lí Thalès trong tam giác sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 8 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Định lí Thalès trong tam giác (Lý thuyết Toán lớp 8) | Kết nối tri thức

Lý thuyết Định lí Thalès trong tam giác

1. Đoạn thẳng tỉ lệ

- Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.

Ví dụ: Tìm tỉ số của các cặp đoạn thẳng có độ dài như sau:

a) AB = 2 cm và CD = 4 cm.

b) MN = 15 cm và PQ = 45 cm.

Hướng dẫn giải

a) Ta có: $\frac{AB}{CD}=\frac{2}{4}=\frac{1}{2}$ .

b) Ta có: $\frac{MN}{PQ}=\frac{15}{45}=\frac{1}{3}$ .

- Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A'B' và C'D' nếu có tỉ lệ thức:

$\frac{AB}{CD}=\frac{A\text{'}B\text{'}}{C\text{'}D\text{'}}hay\frac{AB}{A\text{'}B\text{'}}=\frac{CD}{C\text{'}D\text{'}}$.

Ví dụ: Cho tam giác ABC, AB = 4 cm, AC = 6 cm. Gọi M, N lần lượt là trung điểm của AB và AC. Hãy tính tỉ số $\frac{AM}{AB}và\frac{AN}{AC}$ .

Hướng dẫn giải

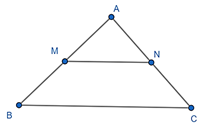
Vì M là trung điểm của AB nên AM = MB = $\frac{1}{2}AB$  = 2 cm

N là trung điểm của AC nên AN = NC = $\frac{1}{2}AC$  = 3 cm

$\frac{AM}{AB}=\frac{2}{4}=\frac{1}{2}$

$\frac{AN}{AC}=\frac{3}{6}=\frac{1}{2}$

Ta thấy: $\frac{AM}{AB}=\frac{AN}{AC}=\frac{1}{2}$ .

2. Định lí Thalès trong tam giác

2.1. Định lí Thalès

Định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

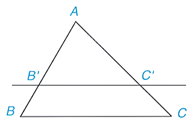
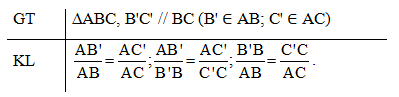
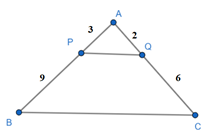
Ví dụ: Tính độ dài AQ trong hình dưới đây biết PQ // BC, AP = 3 cm, PB = 9 cm, QC = 6 cm.

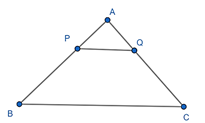
Xét ∆ABC có PQ // BC nên theo định lí Thalès, ta có: $\frac{AP}{PB}\text{\hspace{0.17em}\hspace{0.17em}}=\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}\frac{AQ}{QC}\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}hay\frac{3}{9}\text{\hspace{0.17em}\hspace{0.17em}}=\text{\hspace{0.17em}\hspace{0.17em}}\frac{AQ}{6}$

Suy ra: AQ = $\frac{3.6}{9}$  =  2 cm.

2.2. Định lí Thalès đảo

Định lí Thalès đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

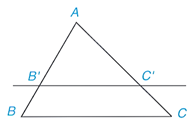
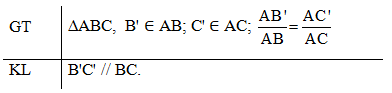
Ví dụ: Quan sát hình dưới đây, chứng minh PQ // BC.

Hướng dẫn giải

Trong ∆ABC, ta có: $\frac{AP}{PB}\text{\hspace{0.17em}\hspace{0.17em}}=\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}\frac{AQ}{QC}=\frac{1}{3}$ .

Áp dụng định lí Thalès đảo

Suy ra: PQ // BC.

Bài tập Định lí Thalès trong tam giác

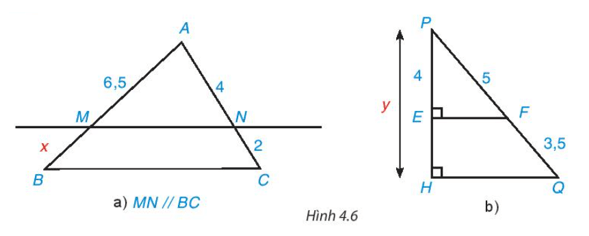
Bài 1: Tìm độ dài x cho hình vẽ sau biết MN // BC.

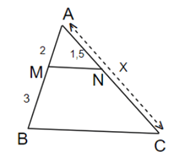
Hướng dẫn giải

Ta có: AB = AM + MB = 2 + 3 = 5.

Áp dụng định lí Thalès trong tam giác ABC có MN // BC

Ta có: $\frac{AM}{AB}\text{\hspace{0.17em}\hspace{0.17em}}=\text{\hspace{0.17em}\hspace{0.17em}}\frac{AN}{AC}$  ⇒ $\frac{2}{5}\text{\hspace{0.17em}\hspace{0.17em}}=\text{\hspace{0.17em}\hspace{0.17em}}\frac{\mathrm{1,5}}{x}$⇒ x = $\frac{\mathrm{5.1,5}}{2}$  = 3,75.

Vậy x = 3,75.

Bài 2: Cho tam giác ABC vuông tại A có AB = 6 cm, BC = 10 cm. Trên đoạn thẳng AB lấy điểm M sao cho AM = 2 cm. Dựng đường thẳng MN vuông góc AB. Tính BN.

Hướng dẫn giải

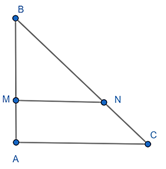
Ta có: AM + MB = AB, suy ra MB = AB – AM = 6 – 2 = 4 (cm).

Ta thấy: MN vuông góc với AB (gt) và AC vuông góc với AB (do tam giác ABC vuông tại A)

Suy ra: MN // AC.

Áp dụng định lí Thalès trong ∆ABC, ta có:

$\frac{BM}{AB}=\frac{BN}{BC}$⇒ BN = $\frac{BM\cdot BC}{AB}=\frac{4\cdot 10}{6}=\frac{20}{3}$ (cm)

Vậy BN = $\frac{20}{3}$ cm.

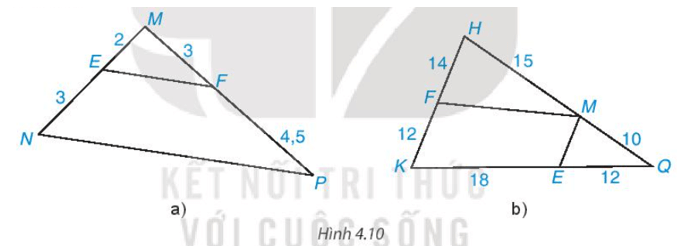
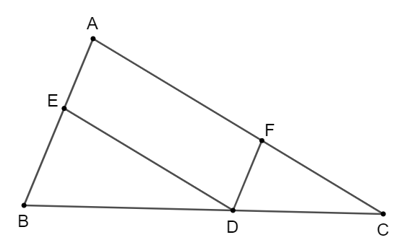
Bài 3: Tìm các cặp đường thẳng song song trong hình vẽ dưới đây và giải thích vì sao chúng song song với nhau?

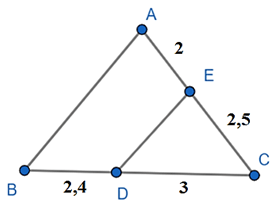
Hướng dẫn giải

Ta có: $\frac{EC}{AE}=\frac{\mathrm{2,5}}{2}=\frac{5}{4}$

$\frac{DC}{BD}=\frac{3}{\mathrm{2,4}}=\frac{5}{4}$

Suy ra $\frac{EC}{AE}=\frac{DC}{BD}$ .

Áp dụng định lí Thalès đảo trong tam giác ABC.

Do đó, DE // AB.

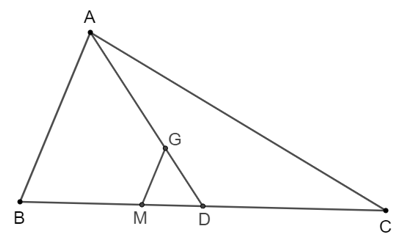
Bài 4: Cho tam giác ABC. Trên cạnh BC lấy điểm D sao cho BC = 2BD. Trên đoạn AD lấy điểm O sao cho $\frac{AO}{OD}=\frac{3}{2}$ . Gọi I là giao điểm của CO và AB. Tính tỉ số $\frac{AI}{IB}$ .

Hướng dẫn giải

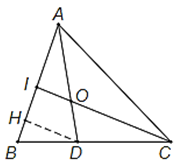
Kẻ thêm DH // CI (H thuộc AB) thì DH // IO.

Áp dụng định lí Thalès vào ∆ADH có DH // IO, ta có:

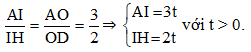
Ta có: BD + DC = BC, suy ra DC = BC – BD = 2BD – BD = BD nên BC = 2DC.

Áp dụng định lí Thalès vào ∆BIC có DH // IC, ta có:

$\frac{BI}{IH}=\frac{BC}{CD}=2$⇒ BI = 2IH = 2 . 2t = 4t

Vậy $\frac{AI}{IB}=\frac{3t}{4t}=\frac{3}{4}$ .

Học tốt Định lí Thalès trong tam giác

Các bài học để học tốt Định lí Thalès trong tam giác Toán lớp 8 hay khác:

15 Bài tập Định lí Thalès trong tam giác (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 8

Với 15 bài tập trắc nghiệm Định lí Thalès trong tam giác Toán lớp 8 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 8.

15 Bài tập Định lí Thalès trong tam giác (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 8

Nội dung đang được cập nhật ...

Xem thêm bài tập trắc nghiệm Toán lớp 8 Kết nối tri thức có đáp án hay khác: