Với giải bài tập Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu sách Kết nối tri thức hay nhất, chi tiết giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 Bài 7.

Giải Toán 8 Kết nối tri thức Bài 7: Lập phương của một tổng. Lập phương của một hiệu

Video Giải Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu - Cô Vũ Chuyên (Giáo viên VietJack)

Giải Toán 8 trang 34

Mở đầu trang 34 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu - Kết nối tri thức

Mở đầu trang 34 Toán 8 Tập 1: Chúng mình đã biết công thức (a + b)² = a² + 2ab + b², còn công thức tính (a + b)³ thì sao nhỉ?

Lời giải:

Ta đưa (a + b)³ về phép nhân đa thức:

(a + b)³ = (a + b)(a + b)².

Lời giải bài tập Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu hay, chi tiết khác:

HĐ1 trang 34 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu - Kết nối tri thức

HĐ1 trang 34 Toán 8 Tập 1: Với hai số a, b bất kì, thực hiện phép tính (a + b)(a + b)². Từ đó rút ra liên hệ giữa (a + b)³ và a³ + 3a²b + 3ab² + b³.

Lời giải:

Ta có (a + b)(a + b)² = (a + b)(a² + 2ab + b²)

= a³ + 2a²b + ab² + a²b + 2ab² + b³

= a³ + (2a²b + a²b) + (ab² + 2ab²) + b³

= a³ + 3a²b + 3ab² + b³.

Ta có (a + b)(a + b)² = (a + b)³; (a + b)(a + b)² = a³ + 3a²b + 3ab² + b³.

Vậy (a + b)³ = a³ + 3a²b + 3ab² + b³.

Lời giải bài tập Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu hay, chi tiết khác:

Luyện tập 1 trang 35 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu - Kết nối tri thức

Luyện tập 1 trang 35 Toán 8 Tập 1:

1. Khai triển

a) (x + 3)³;

b) (x + 2y)³.

2. Rút gọn biểu thức (2x + y)³ – 8x³ – y³.

Lời giải:

1.

a) (x + 3)³ = x³ + 3 . x² . 3 + 3 . x . 3² + 3³ = x³ + 9x² + 27x + 27;

b) (x + 2y)³ = x³ + 3 . x² . 2y + 3 . x . (2y)² + (2y)³

= x³ + 6x²y + 12xy² + 8y³.

2.

(2x + y)³ – 8x³ – y³

= (2x)³ + 3 . (2x)² . y + 3 . 2x . y² + y³ – 8x³ – y³

= 8x³ + 12x²y + 6xy² + y³ – 8x³ – y³

= (8x³ – 8x³) + 12x²y + 6xy² + (y³ – y³)

= 12x²y + 6xy².

Lời giải bài tập Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu hay, chi tiết khác:

Luyện tập 2 trang 35 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu - Kết nối tri thức

Luyện tập 2 trang 35 Toán 8 Tập 1: Viết biểu thức x³ + 9x²y + 27xy² + 27y³ dưới dạng lập phương của một tổng.

Lời giải:

Ta có: x³ + 9x²y + 27xy² + 27y³

= x³ + 3x² . 3y + 3 . x . (3y)² + (3y)³

= (x + 3y)³.

Vậy x³ + 9x²y + 27xy² + 27y³ = (x + 3y)³.

Lời giải bài tập Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu hay, chi tiết khác:

HĐ2 trang 35 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu - Kết nối tri thức

HĐ2 trang 35 Toán 8 Tập 1: Với hai số a, b bất kì, viết a – b = a + (–b) và áp dụng hằng đẳng thức lập phương của một tổng để tính (a – b)³.

Từ đó rút ra liên hệ giữa (a – b)³ và a³ – 3a²b + 3ab² – b³.

Lời giải:

(a – b)³ = [a + (–b)]³ = a³ + 3a²(−b) + 3a(−b)² + (–b)³

= a³ − 3a²b + 3ab² – b³.

Do đó (a – b)³ = a³ – 3a²b + 3ab² – b³.

Lời giải bài tập Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu hay, chi tiết khác:

Luyện tập 3 trang 35 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu - Kết nối tri thức

Luyện tập 3 trang 35 Toán 8 Tập 1: Khai triển (2x – y)³.

Lời giải:

Ta có (2x – y)³ = (2x)³ – 3 . (2x)² . y + 3 . 2x . y² – y³

= 8x³ – 12x²y + 6xy² – y³.

Lời giải bài tập Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu hay, chi tiết khác:

Luyện tập 4 trang 36 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu - Kết nối tri thức

Luyện tập 4 trang 36 Toán 8 Tập 1: Viết biểu thức dưới dạng lập phương của một hiệu

8x³ – 36x²y + 54xy² – 27y³.

Lời giải:

Ta có 8x³ – 36x²y + 54xy² – 27y³

= (2x)³ – 3 . (2x)² . 3y + 3 . (2x) . (3y)² – (3y)³

= (2x – 3y)³.

Lời giải bài tập Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu hay, chi tiết khác:

Vận dụng trang 36 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu - Kết nối tri thức

Vận dụng trang 36 Toán 8 Tập 1: Rút gọn biểu thức: (x – y)³ + (x + y)³.

Lời giải:

Ta có (x – y)³ + (x + y)³

= x³ – 3x²y + 3xy² – y³ + x³ + 3x²y + 3xy² + y³

= (x³ + x³) + (3x²y – 3x²y) + (3xy² + 3xy²) + (y³ – y³)

= 2x³ + 6xy².

Lời giải bài tập Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu hay, chi tiết khác:

Bài 2.7 trang 36 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu - Kết nối tri thức

Bài 2.7 trang 36 Toán 8 Tập 1: Khai triển:

a) ${\left(x^2+2y\right)}^3$ ;

b) ${\left(\frac{1}{2}x-1\right)}^3$ .

Lời giải:

a) ${\left(x^2+2y\right)}^3={\left(x^2\right)}^3+3.{\left(x^2\right)}^2.2y+3.x^2.{\left(2y\right)}^2+{\left(2y\right)}^3$

= x⁶ + 3.x⁴.2y + 3.x².4y² + 8y³

= x⁶ + 6x⁴y + 12x²y² + 8y³;

b) ${\left(\frac{1}{2}x-1\right)}^3={\left(\frac{1}{2}x\right)}^3-3.{\left(\frac{1}{2}x\right)}^2.1+3.\frac{1}{2}x.1^2-1^3$

$=\frac{1}{8}{x}^3-3.\frac{1}{4}{x}^2+3.\frac{1}{2}x-1$

$=\frac{1}{8}{x}^3-\frac{3}{4}{x}^2+\frac{3}{2}x-1$.

Lời giải bài tập Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu hay, chi tiết khác:

Bài 2.8 trang 36 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu - Kết nối tri thức

Bài 2.8 trang 36 Toán 8 Tập 1: Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc một hiệu.

a) 27 + 54x + 36x² + 8x³;

b) 64x³ – 144x²y + 108xy² – 27y³.

Lời giải:

a) 27 + 54x + 36x² + 8x³

= 3³ + 3 . 3² . 2x + 3 . 3 . (2x)² + (2x)³

= (3 + 2x)³;

b) 64x³ – 144x²y + 108xy² – 27y³

= (4x)³ – 3 . (4x)² . 3y + 3 . 4x . (3y)² – (3y)³

= (4x – 3y)³.

Lời giải bài tập Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu hay, chi tiết khác:

Bài 2.9 trang 36 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu - Kết nối tri thức

Bài 2.9 trang 36 Toán 8 Tập 1: Tính nhanh giá trị của biểu thức:

a) x³ + 9x² + 27x + 27 tại x = 7;

b) 27 – 54x + 36x² – 8x³ tại x = 6,5.

Lời giải:

a) Ta có: x³ + 9x² + 27x + 27

= x³ + 3 . x² . 3 + 3 . x . 3² + 3³ = (x + 3)³.

Thay x = 7 vào biểu thức (x + 3)³, ta được:

(7 + 3)³ = 10³ = 1 000.

b) Ta có 27 – 54x + 36x² – 8x³

= 3³ – 3 . 3² . 2x + 3 . 3 . (2x)² – (2x)³

= (3 – 2x)³.

Thay x = 6,5 vào biểu thức (3 – 2x)³, ta được:

(3 – 2 . 6,5)³ = (3 – 13)³ = (–10)³ = –1 000.

Lời giải bài tập Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu hay, chi tiết khác:

Bài 2.10 trang 36 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu - Kết nối tri thức

Bài 2.10 trang 36 Toán 8 Tập 1: Rút gọn các biểu thức sau:

a) (x – 2y)³ + (x + 2y)³;

b) (3x + 2y)³ + (3x – 2y)³.

Lời giải:

a) (x – 2y)³ + (x + 2y)³

= x³ – 3 . x² . 2y + 3 . x . (2y)² – (2y)³ + x³ + 3 . x² . 2y + 3 . x . (2y)² + (2y)³

= x³ – 6x²y + 12xy²– 8y³ + x³ + 6x²y + 12xy²+ 8y³

= (x³ + x³) + (6x²y – 6x²y) + (12xy²+ 12xy²) + (8y³ – 8y³)

= 2x³ + 24xy².

b) (3x + 2y)³ + (3x – 2y)³

= (3x)³ + 3 . (3x)² . 2y + 3 . 3x . (2y)² + (2y)³ + (3x)³ – 3 . (3x)² . 2y + 3 . 3x . (2y)² – (2y)³

= (3x)³ + 3 . 3x . (2y)² + (3x)³ + 3 . 3x . (2y)²

= 27x³ + 36xy² + 27x³ + 36xy²

= 54x³ + 72xy².

Lời giải bài tập Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu hay, chi tiết khác:

Bài 2.11 trang 36 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu - Kết nối tri thức

Bài 2.11 trang 36 Toán 8 Tập 1: Chứng minh (a – b)³ = – (b – a)³.

Lời giải:

Ta có

• (a – b)³ = a³ – 3a²b + 3ab² – b³;

• – (b – a)³ = – (b³ – 3b²a + 3ba² – a³)

= – b³ + 3b²a – 3ba² + a³ = a³ – 3a²b + 3ab² – b³.

Vậy (a – b)³ = – (b – a)³.

Lời giải bài tập Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu hay, chi tiết khác:

SBT Toán 8 Kết nối tri thức Bài 7: Lập phương của một tổng. Lập phương của một hiệu

Với giải sách bài tập Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 8 dễ dàng làm bài tập trong SBT Toán 8 Bài 7.

Giải SBT Toán 8 Kết nối tri thức Bài 7: Lập phương của một tổng. Lập phương của một hiệu

Vở thực hành Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu - Kết nối tri thức

Với giải vở thực hành Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 8 dễ dàng làm bài tập về nhà trong VTH Toán 8 Bài 7.

Giải vở thực hành Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu - Kết nối tri thức

B – CÂU HỎI TRẮC NGHIỆM

Chọn phương án đúng trong mỗi câu sau:

Lập phương của một tổng. Lập phương của một hiệu (Lý thuyết Toán lớp 8) | Kết nối tri thức

Với tóm tắt lý thuyết Toán 8 Bài 7: Lập phương của một tổng. Lập phương của một hiệu sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 8 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Lập phương của một tổng. Lập phương của một hiệu (Lý thuyết Toán lớp 8) | Kết nối tri thức

Lý thuyết Lập phương của một tổng. Lập phương của một hiệu

1. Lập phương của một tổng

+ Với hai số a, b bất kì ta thức hiện phép tính:

(a + b).(a + b)² = (a + b).(a² + 2ab + b²)

                       = a³ + 3a²b + 3ab² + b³

Vậy (a + b).(a + b)² = (a + b)³ = a³ + 3a²b + 3ab² + b³.

+ Với A, B là hai biểu thức bất kì, ta có:

(A + B)³ = A³ + 3A²B + 3AB² + B³.

Ví dụ 1: Khai triển:

a) (x + 3)³ = x³ + 3.x².3 + 3.x.3² + 3³ = x³ + 9x² + 27x + 27

b) (3x + y)³ = (3x)³ + 3.(3x)².y + 3.3x.y² + y³ = 27x³ + 27x²y + 9xy² + y³.

Ví dụ 2: Viết biểu thức x³ + 12x² + 48x + 6 dưới dạng lập phương của một tổng

Ta có: x³ + 12x² + 48x + 64 = x³ + 3.x².4 + 3.x.4² + 4³ = (x + 4)³.

2. Lập phương của một hiệu

+ Với hai số a, b bất kì ta viết a – b = a + (–b) và áp dụng hằng đẳng thức lập phương của một tổng để tính (a – b)³

Ta có: [a + (–b)]³ = a³ + 3a².(–b) + 3a.(–b)² + (–b)³ = a³ – 3a²b + 3ab² – b³.

Vậy (a – b)³ = a³ – 3a²b + 3ab² – b³.

+ Với A, B là hai biểu thức bất kì, ta có:

(A – B)³ = A³ – 3A²B + 3AB² – B³.

Ví dụ 3: Khai triển:

a) (x – 3)³ = x³ – 3.x².3 + 3.x.3² – 3³ = x³ – 9x² + 27x – 27

b) (3x – y)³ = (3x)³ – 3.(3x)².y + 3.3x.y² – y³ = 27x³ – 27x²y + 9xy² – y³.

Ví dụ 4: Viết biểu thức 8x³ – 36x² + 54x – 27 dưới dạng lập phương của một hiệu.

Ta có: 8x³ – 36x² + 54x – 27 = (2x)³ – 3.4x².3 + 3.2x.3² – 3³ = (2x – 3)³.

Bài tập Lập phương của một tổng. Lập phương của một hiệu

Bài 1. Khai triển:

a) (x + y²)³;                                                 

b)(${\left(x-\frac{1}{2}\mathrm{y)}\right)}^3.$

Hướng dẫn giải

a) (x + y²)³ = x³ + 3x²y² + 3xy⁴ + y⁶;

b)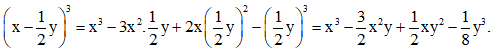

Bài 2. Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc một hiệu.

a) 125 + 150x + 60x² + 8x³;

b) 64x³ – 48x² + 12x – 1.

Hướng dẫn giải

a) 125 + 150x + 60x² + 8x³ = 5³ + 3.2x.5² + 3.(2x)².5 + (2x)³ = (5 + 2x)³

b) 64x³ – 48x² + 12x – 1 = (4x)³ – 3.(4x)².1 + 3.4x.(–1)² – (1)³ = (4x – 1)³.

Bài 3. Tính nhanh giá trị biểu thức:

a) 125 + 75x + 15x² + x³ tại x = 5;

b) x³ – 9x² + 27x – 27 tại x = 7.

Hướng dẫn giải

a) 125 + 75x + 15x² + x³ = (5 + x)³

Thay x = 5, ta được (5 + 5)³ = 10³ = 1000.

b) x³ – 9x² + 27x – 27 = (x – 3)³

Thay x = 7, ta được (7 – 3)³ = 4³ = 64.

Bài 4. Rút gọn các biểu thức sau:

a) (x – y)³ + (x + y)³;                                  

b) (3x + 4)³ + (3x – 4)³.

Hướng dẫn giải

a) (x – y)³ + (x + y)³

= x³ – 3x²y + 3xy² – y³ + x³ + 3x²y + 3xy² + y³

= 2x³ + 6xy²;

b) (3x + 4)³ + (3x – 4)³

= 27x³ + 108x² + 144x + 64 + 27x³ – 108x² + 144x – 64

= 54x³ + 288x.

Học tốt Lập phương của một tổng. Lập phương của một hiệu

Các bài học để học tốt Lập phương của một tổng. Lập phương của một hiệu Toán lớp 8 hay khác:

15 Bài tập Lập phương của một tổng. Lập phương của một hiệu (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 8

Với 15 bài tập trắc nghiệm Lập phương của một tổng. Lập phương của một hiệu Toán lớp 8 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 8.

15 Bài tập Lập phương của một tổng. Lập phương của một hiệu (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 8

Câu 1. Chọn câu đúng?

A. ${\left(\text{A + B}\right)}^{\text{3}}{\text{= A}}^{\text{3}}{\text{+ 3A}}^{\text{2}}{\text{B + 3AB}}^{\text{2}}{\text{+ B}}^{\text{3}}$

B. ${\left(\text{A}-\text{B}\right)}^{\text{3}}{\text{=A}}^{\text{3}}-{\text{3A}}^{\text{2}}\text{B}-{\text{3AB}}^{\text{2}}-{\text{B}}^{\text{3}}$

C. ${\left(\text{A + B}\right)}^{\text{3}}{\text{= A}}^{\text{3}}{\text{+ B}}^{\text{3}}$

D. ${\left(\text{A}-\text{B}\right)}^{\text{3}}{\text{= A}}^{\text{3}}-{\text{B}}^{\text{3}}$

Câu 2. Viết biểu thức ${\text{x}}^3+3{\text{x}}^2+3\text{x}+1$ dưới dạng lập phương của một tổng

A. ${\left(\text{x}+1\right)}^3$

B. ${\left(\text{x}+3\right)}^3$

C. ${\left(\text{x}-1\right)}^3$

D. ${\left(\text{x}-3\right)}^3$

Câu 3. Khai triển hằng đẳng thức ${\left(\text{x}-2\right)}^3$ ta được

A. ${\text{x}}^{\text{3}}-{\text{6x}}^{\text{2}}\text{+ 12x}-\text{8}$

B. ${\text{x}}^{\text{3}}{\text{+ 6x}}^{\text{2}}\text{+ 12x + 8}$

C. ${\text{x}}^{\text{3}}-{\text{6x}}^{\text{2}}-\text{12x}-\text{8}$

D. ${\text{x}}^{\text{3}}{\text{+ 6x}}^{\text{2}}-\text{12x}+\text{8}$

Câu 4. Cho $\text{A +}\frac{\text{3}}{\text{4}}{\text{x}}^{\text{2}}-\frac{\text{3}}{\text{2}}\text{x + 1 =}{\left(\text{B + 1}\right)}^{\text{3}}$. Khi đó

A. $\text{A =}-\frac{{\text{x}}^{\text{3}}}{\text{8}}\text{; B =}\frac{\text{x}}{\text{2}}$

B. $\text{A =}-\frac{{\text{x}}^{\text{3}}}{\text{8}}\text{; B =}-\frac{\text{x}}{\text{2}}$

C. $\text{A =}-\frac{{\text{x}}^{\text{3}}}{\text{8}}\text{; B =}-\frac{\text{x}}{\text{8}}$

D. $\text{A =}\frac{{\text{x}}^{\text{3}}}{\text{8}}\text{; B =}\frac{\text{x}}{\text{8}}$

Câu 5. Viết biểu thức ${\text{8 − 36x + 54x}}^2-27{\text{x}}^3$ dưới dạng lập phương của một tổng hoặc một hiệu ta được

A. ${\left(3\text{x}+2\right)}^3$

B. ${\left(2-3\text{x}\right)}^3$

C. ${\left(8-27\text{x}\right)}^3$

D. ${\left(3\text{x}-2\right)}^3$

Câu 6. Kết quả phép nhân: $\left({\text{x}}^2-2\text{x}+1\right)\left(\text{x}–1\right)=$

A. ${\text{x}}^3-3{\text{x}}^2+3\text{x}-1$

B. ${\text{x}}^3+3{\text{x}}^2+3\text{x}-1$;

C. ${\text{x}}^3-3{\text{x}}^2+3\text{x}-1$;

D. ${\text{x}}^3+3{\text{x}}^2+3\text{x}-1$

Câu 7. Cho biểu thức

$\text{H=}\left(\text{x}+5\right)\left({\text{x}}^2-5\text{x}+25\right)-{\left(2\text{x}+1\right)}^3$ $+7{\left(\text{x}-1\right)}^3-3\text{x}\left(-1\text{1x}+5\right)$. Khi đó

A. H là một số chia hết cho 12.

B. H là một số chẵn.

C. H là một số lẻ.

D. H là một số chính phương.

Câu 8. Tính giá trị của biểu thức $\text{M}={\left(\text{x}+2\text{y}\right)}^3-6{\left(\text{x}+2\text{y}\right)}^2$ $+12\left(\text{x}+2\text{y}\right)-8$ tại x = 20, y = 1

A. 4000

B. 6000

C. 8000

D. 2000

Câu 9. Cho hai biểu thức

$P={\left(4x+1\right)}^3-\left(4x+3\right)\left(16x^2+3\right);$

$Q={\left(x-2\right)}^3-x\left(x+1\right)\left(x-1\right)+6x\left(x-3\right)+5x.$

Tìm mối quan hệ giữa hai biểu thức P, Q?

A. P = – Q

B. P = 2Q

C. P = Q

D. $\text{P =}\frac{\text{1}}{\text{2}}\text{Q}$

Câu 10. Rút gọn biểu thức

$P=8x^3-12x^{2}y+6x{y}^2-y^3+12x^2-12xy+3y^2+6x-3y+11$ ta được

A. $\text{P}={\left(\text{2x}-\text{y}-\text{1}\right)}^{\text{3}}\text{+ 10}$

B. $\text{P}={\left(2\text{x + y}-1\right)}^3+10$

C. $\text{P}={\left(2\text{x}-\text{y}+1\right)}^3+10$

D. $\text{P}={\left(2\text{x}-y-1\right)}^3-10$

Câu 11. Cho biết

$\text{Q}={\left(2\text{x}-1\right)}^3-8\text{x}\left(\text{x}+1\right)\left(\text{x}-1\right)+2\text{x}\left(6\text{x}-5\right)$ $=\text{ax}-\text{b}\left(\text{a, b}\in \mathbb{Z}\right)$. Khi đó

A. a = – 4; b = 1

B. a = 4; b = – 1

C. a = 4; b = 1

D. a = – 4; b = – 1

Câu 12. Cho hai biểu thức $\text{P}={\left(\text{4x + 1}\right)}^{\text{3}}-\left(\text{4x + 3}\right){\text{(16x}}^{\text{2}}\text{+ 3);}$$\text{Q =}{\left(\text{x}-\text{2}\right)}^{\text{3}}-\text{x}\left(\text{x + 1}\right)\left(\text{x}-\text{1}\right)\text{+ 6x}\left(\text{x}-\text{3}\right)\text{+ 5x}$. So sánh P và Q?

A. P < Q

B. P = –Q

C. P = Q

D. P > Q

Câu 13. Cho 2x - y = 9. Giá trị của biểu thức $A=8x^3-12x^{2}y+6x{y}^2-y^3+12x^2$ $-12xy+3y^2+6x-3y+11$ là

A. A = 1001

B. A = 1000

C. A = 1010

D. A = 900

Câu 14. Giá trị của biểu thức $Q=a^3-b^3$ biết a - b = 4 và ab = -3 là

A. Q = 100

B. Q = 64

C. Q = 28

D. Q = 36

Câu 15. Cho a + b + c = 0 . Giá trị của biểu thức $B=a^3+b^3+c^3-3abc$

A. B = 0

B. B = 1

C. B = – 1

D. Không xác định được.

Xem thêm bài tập trắc nghiệm Toán lớp 8 Kết nối tri thức có đáp án hay khác: