Với giải bài tập Toán 9 Bài 5: Bất đẳng thức và tính chất sách Kết nối tri thức hay nhất, chi tiết giúp học sinh lớp 9 dễ dàng làm bài tập Toán 9 Bài 5.

Giải Toán 9 Kết nối tri thức Bài 5: Bất đẳng thức và tính chất

Video Giải Toán 9 Bài 5: Bất đẳng thức và tính chất - Cô Ngô Vân (Giáo viên VietJack)

Giải Toán 9 trang 31

Mở đầu trang 31 Toán 9 Tập 2 | Kết nối tri thức Giải Toán 9

Giải Toán 9 Bài 5: Bất đẳng thức và tính chất - Kết nối tri thức

Mở đầu trang 31 Toán 9 Tập 2: Khi đi đường, chúng ta có thể thấy các biển báo giao thông báo hiệu giới hạn tốc độ mà xe cơ giới được phép đi. Em có biết ý nghĩa của biển báo giao thông ở Hình 2.3 (biển báo giới hạn tốc độ tối đa cho phép theo xe, trên từng làn đường) không?

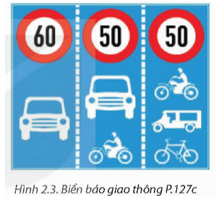
Lời giải:

– Hình 2.3 là Biển ghép tốc độ tối đa cho phép theo phương tiện, trên từng làn đường.

– Ý nghĩa của biển báo giao thông ở Hình 2.3:

⦁ Làn trái: chỉ dành riêng cho ô tô với tốc độ tối đa là 60 km/h.

⦁ Làn giữa: dành cho ô tô và xe máy với tốc độ tối đa là 50 km/h.

⦁ Làn phải: dành cho xe máy, xe ba bánh và xe đạp với tốc độ tối đa là 50 km/h.

Lời giải bài tập Toán 9 Bài 5: Bất đẳng thức và tính chất hay, chi tiết khác:

Câu hỏi trang 31 Toán 9 Tập 1 | Kết nối tri thức Giải Toán 9

Giải Toán 9 Bài 5: Bất đẳng thức và tính chất - Kết nối tri thức

Câu hỏi trang 31 Toán 9 Tập 1: Thay $\boxed{?}$ trong các biểu thức sau bằng dấu thích hợp (=, >, <).

a) $-\mathrm{34,2}\boxed{?}-27;$

b) $\frac{6}{-8}\boxed{?}-\frac{3}{4};$

c) $2024\boxed{?}1954.$

Lời giải:

a) $-\mathrm{34,2}\boxed{<}-27;$

b) $\frac{6}{-8}\boxed{=}-\frac{3}{4};$

c) $2024\boxed{>}1954.$

Lời giải bài tập Toán 9 Bài 5: Bất đẳng thức và tính chất hay, chi tiết khác:

Luyện tập 1 trang 32 Toán 9 Tập 1 | Kết nối tri thức Giải Toán 9

Giải Toán 9 Bài 5: Bất đẳng thức và tính chất - Kết nối tri thức

Luyện tập 1 trang 32 Toán 9 Tập 1: Biển báo giao thông R.306 (H.2.4) báo tốc độ tối thiểu cho các xe cơ giới. Biển có hiệu lực bắt buộc các loại xe cơ giới vận hành với tốc độ không nhỏ hơn trị số ghi trên biển trong điều kiện giao thông thuận lợi và an toàn.

Nếu một ô tô đi trên đường đó với tốc độ a (km/h) thì a phải thoả mãn điều kiện nào trong các điều kiện sau?

A. a < 60.

B. a > 60.

C. a ≥ 60.

D. a ≤ 60.

Lời giải:

Đáp án đúng là: C

Do biển có hiệu lực bắt buộc các loại xe cơ giới vận hành với tốc độ không nhỏ hơn trị số ghi trên biển, nên theo Hình 2.4 thì tốc độ của ô tô đi trên đường đó không nhỏ hơn 60 km/h tức là có thể bằng 60 km/h hoặc lớn hơn 60 km/h.

Tức là a ≥ 60. Vậy ta chọn phương án C.

Lời giải bài tập Toán 9 Bài 5: Bất đẳng thức và tính chất hay, chi tiết khác:

Luyện tập 2 trang 33 Toán 9 Tập 1 | Kết nối tri thức Giải Toán 9

Giải Toán 9 Bài 5: Bất đẳng thức và tính chất - Kết nối tri thức

Luyện tập 2 trang 33 Toán 9 Tập 1: Chứng minh rằng:

a) $\frac{2024}{1000}>\mathrm{1,9};$

b) $-\frac{2022}{2023}>-\mathrm{1,1.}$

Lời giải:

a) Ta có $\frac{2024}{1000}=\frac{2000}{1000}+\frac{24}{1000}=2+\frac{24}{1000}>2$ và 2 > 1,9 nên $\frac{2024}{1000}>\mathrm{1,9};$

b) Ta có $\frac{2022}{2023}=\frac{2023}{2023}-\frac{1}{2023}=1-\frac{1}{2023}.$

Do đó $-\frac{2022}{2023}=-1+\frac{1}{2023}>-1.$

Mà –1 > –1,1 nên $-\frac{2022}{2023}>-\mathrm{1,1.}$

Lời giải bài tập Toán 9 Bài 5: Bất đẳng thức và tính chất hay, chi tiết khác:

Vận dụng 1 trang 33 Toán 9 Tập 1 | Kết nối tri thức Giải Toán 9

Giải Toán 9 Bài 5: Bất đẳng thức và tính chất - Kết nối tri thức

Vận dụng 1 trang 33 Toán 9 Tập 1: Viết các bất đẳng thức để mô tả tốc độ cho phép trong tình huống mở đầu:

a) Ô tô ở làn giữa;

b) Xe máy ở làn bên phải.

Lời giải:

a) Gọi tốc độ của ô tô di duyển ở làn giữa là a (km/h), bất đẳng thức mô tả tốc độ cho phép ô tô di chuyển ở làn giữa là a ≤ 50.

b) Gọi tốc độ của xe máy di duyển ở làn bên phải là b (km/h), bất đẳng thức mô tả tốc độ cho phép xe máy di duyển ở làn bên phải là b ≤ 50.

Lời giải bài tập Toán 9 Bài 5: Bất đẳng thức và tính chất hay, chi tiết khác:

Luyện tập 3 trang 34 Toán 9 Tập 1 | Kết nối tri thức Giải Toán 9

Giải Toán 9 Bài 5: Bất đẳng thức và tính chất - Kết nối tri thức

Luyện tập 3 trang 34 Toán 9 Tập 1: Không thực hiện phép tính, hãy so sánh:

a) 19 + 2 023 và –31 + 2 023;

b) $\sqrt{2}+2$ và 4.

Lời giải:

a) Vì 19 > –31 nên 19 + 2 023 > –31 + 2 023.

b) Ta có $2=\sqrt{4}.$

Vì 2 < 4 nên $\sqrt{2}<\sqrt{4}$ hay $\sqrt{2}<2.$

Suy ra $\sqrt{2}+2<2+2$ hay $\sqrt{2}+2<4.$

Lời giải bài tập Toán 9 Bài 5: Bất đẳng thức và tính chất hay, chi tiết khác:

Luyện tập 4 trang 35 Toán 9 Tập 1 | Kết nối tri thức Giải Toán 9

Giải Toán 9 Bài 5: Bất đẳng thức và tính chất - Kết nối tri thức

Luyện tập 4 trang 35 Toán 9 Tập 1: Thay $\boxed{?}$ trong các biểu thức sau bởi dấu thích hợp (<, >) để được khẳng định đúng.

a) $13\cdot \left(-\mathrm{10,5}\right)\boxed{?}13\cdot \mathrm{11,2};$

b) $\left(-13\right)\cdot \left(-\mathrm{10,5}\right)\boxed{?}\left(-13\right)\cdot \mathrm{11,2.}$

Lời giải:

a) Ta có –10,5 < 11,2 nên 13 . (–10,5) < 13 . 11,2.

Vậy $13\cdot \left(-\mathrm{10,5}\right)\boxed{<}13\cdot \mathrm{11,2.}$

b) Ta có –10,5 < 11,2 nên (–13) . (–10,5) > (–13) . 11,2.

Vậy $\left(-13\right)\cdot \left(-\mathrm{10,5}\right)\boxed{>}\left(-13\right)\cdot \mathrm{11,2.}$

Lời giải bài tập Toán 9 Bài 5: Bất đẳng thức và tính chất hay, chi tiết khác:

Vận dụng 2 trang 35 Toán 9 Tập 1 | Kết nối tri thức Giải Toán 9

Giải Toán 9 Bài 5: Bất đẳng thức và tính chất - Kết nối tri thức

Vận dụng 2 trang 35 Toán 9 Tập 1: Một nhà tài trợ dự kiến tổ chức một buổi đi dã ngoại tập thể nhằm giúp các bạn học sinh vùng cao trải nghiệm thực tế tại một trang trại trong 1 ngày (từ 14h00 ngày hôm trước đến 12h00 ngày hôm sau). Cho biết số tiền tài trợ dự kiến là 30 triệu đồng và giá thuê các dịch vụ và phòng nghỉ là 17 triệu đồng 1 ngày, giá mỗi suất ăn trưa, ăn tối là 60 000 đồng và mỗi suất ăn sáng là 30 000 đồng. Hỏi có thể tổ chức cho nhiều nhất bao nhiêu bạn tham gia được?

Lời giải:

Gọi x là số bạn học sinh có thể tham gia được (học sinh) (x ∈ ℕ*).

Theo bài, số tiền còn lại sau khi thu dịch vụ và phòng nghỉ là:

30 – 17 = 13 (triệu đồng) = 13 000 (nghìn đồng).

Số tiền ăn sáng, ăn trưa và ăn tối của 1 bạn là:

60 000 + 30 000 + 60 000 = 150 000 (đồng) = 150 (nghìn đồng).

Như vậy, số tiền ăn của x bạn học sinh trong chuyến đi là 150x (nghìn đồng).

Khi đó ta có: 150x ≤ 13 000.

Suy ra $x\le \frac{13000}{150}$ hay $x\le \frac{260}{3}=\mathrm{86,}\left(6\right).$

Mà x ∈ ℕ* nên số bạn học sinh nhiều nhất có thể tham gia được là 86 bạn.

Vậy nhà tài trợ có thể tổ chức cho nhiều nhất 86 bạn tham gia được chuyến đi.

Lời giải bài tập Toán 9 Bài 5: Bất đẳng thức và tính chất hay, chi tiết khác:

Bài 2.6 trang 35 Toán 9 Tập 1 | Kết nối tri thức Giải Toán 9

Giải Toán 9 Bài 5: Bất đẳng thức và tính chất - Kết nối tri thức

Bài 2.6 trang 35 Toán 9 Tập 1: Dùng kí hiệu để viết bất đẳng thức tương ứng với mỗi truờng hợp sau:

a) x nhỏ hơn hoặc bằng –2;

b) m là số âm;

c) y là số dương;

d) p lớn hơn hoặc bằng 2 024.

Lời giải:

a) x ≤ –2;

b) m < 0;

c) y > 0;

d) p ≥ 2 024.

Lời giải bài tập Toán 9 Bài 5: Bất đẳng thức và tính chất hay, chi tiết khác:

Bài 2.7 trang 35 Toán 9 Tập 1 | Kết nối tri thức Giải Toán 9

Giải Toán 9 Bài 5: Bất đẳng thức và tính chất - Kết nối tri thức

Bài 2.7 trang 35 Toán 9 Tập 1: Viết một bất đẳng thức phù hợp trong mỗi trường hợp sau:

a) Bạn phải ít nhất 18 tuổi mới được phép lái ô tô;

b) Xe buýt chở được tối đa 45 người;

c) Mức lương tối thiểu cho một giờ làm việc của người lao động là 20 000 đồng.

Lời giải:

a) Gọi x (tuổi) là số tuổi của bạn, khi đó bất đẳng thức phù hợp cho “Bạn phải ít nhất 18 tuổi mới được phép lái ô tô” là x ≥ 18.

b) Gọi y (người) là số người xe buýt có thể chở được, khi đó bất đẳng thức phù hợp cho “Xe buýt chở được tối đa 45 người” là y ≤ 45.

c) Gọi z (đồng) là mức lương cho một giờ làm việc của người lao động, khi đó bất đẳng thức phù hợp cho “Mức lương tối thiểu cho một giờ làm việc của người lao động là 20 000 đồng” là z ≥ 20 000.

Lời giải bài tập Toán 9 Bài 5: Bất đẳng thức và tính chất hay, chi tiết khác:

Bài 2.8 trang 35 Toán 9 Tập 1 | Kết nối tri thức Giải Toán 9

Giải Toán 9 Bài 5: Bất đẳng thức và tính chất - Kết nối tri thức

Bài 2.8 trang 35 Toán 9 Tập 1: Không thực hiện phép tính, hãy chứng minh:

a) 2 . (–7) + 2 023 < 2 . (–1) + 2 023;

b) (–3) . (–8) + 1 975 > (–3) . (–7) + 1 975.

Lời giải:

a) Vì –7 < –1 nên 2 . (–7) < 2 . (–1)

Do đó 2 . (–7) + 2 023 < 2 . (–1) + 2 023.

b) Vì –8 < –7 nên (–3) . (–8) > (–3) . (–7)

Do đó (–3) . (–8) + 1 975 > (–3) . (–7) + 1 975.

Lời giải bài tập Toán 9 Bài 5: Bất đẳng thức và tính chất hay, chi tiết khác:

Bài 2.9 trang 35 Toán 9 Tập 1 | Kết nối tri thức Giải Toán 9

Giải Toán 9 Bài 5: Bất đẳng thức và tính chất - Kết nối tri thức

Bài 2.9 trang 35 Toán 9 Tập 1: Cho a < b, hãy so sánh:

a) 5a + 7 và 5b + 7;

b) –3a – 9 và –3b – 9.

Lời giải:

a) Vì a < b nên 5a < 5b, suy ra 5a + 7 < 5b + 7.

Vậy 5a + 7 < 5b + 7.

b) Vì a < b nên –3a > –3b, suy ra –3a – 9 > –3b – 9.

Vậy –3a – 9 > –3b – 9.

Lời giải bài tập Toán 9 Bài 5: Bất đẳng thức và tính chất hay, chi tiết khác:

Bài 2.10 trang 35 Toán 9 Tập 1 | Kết nối tri thức Giải Toán 9

Giải Toán 9 Bài 5: Bất đẳng thức và tính chất - Kết nối tri thức

Bài 2.10 trang 35 Toán 9 Tập 1: So sánh hai số a và b, nếu:

a) a + 1 954 < b + 1 954;

b) –2a > –2b.

Lời giải:

a) Ta có: a + 1 954 < b + 1 954

Suy ra: a + 1 954 – 1 954 < b + 1 954 – 1 954 hay a < b.

Vậy a < b.

b) Ta có: –2a > –2b nên $–2a\cdot \left(-\frac{1}{2}\right)<–2b\cdot \left(-\frac{1}{2}\right),$ hay a < b.

Vậy a < b.

Lời giải bài tập Toán 9 Bài 5: Bất đẳng thức và tính chất hay, chi tiết khác:

Bài 2.11 trang 35 Toán 9 Tập 1 | Kết nối tri thức Giải Toán 9

Giải Toán 9 Bài 5: Bất đẳng thức và tính chất - Kết nối tri thức

Bài 2.11 trang 35 Toán 9 Tập 1: Chứng minh rằng:

a) $-\frac{2023}{2024}>-\frac{2024}{2023};$

b) $\frac{34}{11}>\frac{26}{9}.$

Lời giải:

a) Ta có: $\frac{2023}{2024}=\frac{2024-1}{2024}=1-\frac{1}{2024}<1$ và $\frac{2024}{2023}=\frac{2023+1}{2023}=1+\frac{1}{2023}>1$

Suy ra $\frac{2023}{2024}<\frac{2024}{2023},$do đó $-\frac{2023}{2024}>-\frac{2024}{2023}.$

b) Ta có $\frac{34}{11}=\frac{33+1}{11}=3+\frac{1}{11}>3$ và $\frac{26}{9}=\frac{27-1}{9}=3-\frac{1}{9}<3.$

Suy ra $\frac{34}{11}>\frac{26}{9}.$

Lời giải bài tập Toán 9 Bài 5: Bất đẳng thức và tính chất hay, chi tiết khác: