Giải Toán lớp 6 Cánh diều Bài 5: Số thập phân

Với giải bài tập Toán lớp 6 Bài 5: Số thập phân sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 6 Bài 5:

Trả lời câu hỏi giữa bài

Giải Toán 6 trang 44 Tập 2

Câu hỏi khởi động trang 44 Toán 6 Tập 2 Cánh diều | Giải Toán lớp 6

Giải Toán lớp 6 Cánh diều Bài 5: Số thập phân

Câu hỏi khởi động trang 44 Toán lớp 6 Tập 2: Bản tin Vietnamnet ngày 24/01/2016 viết: “lúc 6 giờ sáng nay, theo ghi nhận của cơ quan khí tượng, nhiệt độ tại hàng loạt khu vực miền núi đã xuống dưới 0 °C như: Mẫu Sơn (Lạng Sơn) là - 4 °C, Sa Pa (Lào Cai) là - 2 °C, Tam Đảo (Vĩnh Phúc) là- 0,4 °C và Đồng Văn (Hà Giang) là – 0,2 °C.

Tại các tỉnh đồng bằng, nhiệt độ cũng đồng loạt hạ xuống dưới 7 °C, trong đó tại Hà Đông (Hà Nội) là 6,5 ^oC, Hải Phòng là 5.4 °C, Bắc Giang giảm còn 5.6 °C, ..

Những số - 0,4; - 0,2 có phải là các số thập phân không?

Trong các số - 0.4; - 0,2; 6,5; 5,4; 5,6 số nào lớn nhất?  Số nào nhỏ nhất?

Lời giải:

Sau bài học này ta có thể trả lời được:

Các số - 0,4; -0,2 là các số thập phân.

Ta so sánh các số thập phân trên bằng cách chia làm hai nhóm:

- Nhóm 1 gồm các số thập phân âm: -0,4 và – 0,2;

- Nhóm 2 gồm các số thập phân dương: 5,4; 5,6 và 6,5.

Vì số thập phân âm luôn nhỏ hơn số thập phân dương nên ta sẽ so sánh các số trong từng  nhóm với nhau.

Nhóm 1:  Số đối với số thập phân – 0,4 là 0,4, còn số đối với số thập phân -0,2 là 0,2.

Hai số thập phân này có cùng phần nguyên, kể từ trái sang cặp chữ số cùng hàng ở sau dấu phẩy khác nhau là cặp chữ số ở hàng phần mười. Do 4 > 2 nên 0,4 > 0,2 suy ra -0,4 < - 0,2.

Nhóm 2: 5,4 và 5,6 có cùng phần nguyên, kể từ trái sang cặp chữ số cùng hàng ở sau dấu phẩy khác nhau là cặp chữ số ở hàng phần mười. Do 4 < 6 nên 5,4 < 5,6.

Ta có 5 < 6 nên 5,6 < 6,5.

Do đó, ta có: 5,4 < 5,6 < 6,5.

Suy ra -0,4 < -0,2 < 5,4 < 5,6 < 6,5.

Vậy số thập phân lớn nhất là 6,5, số thập phân bé nhất là – 0,4.

Lời giải Toán 6 Bài 5: Số thập phân hay, chi tiết khác:

Hoạt động 1 trang 44 Toán 6 Tập 2 Cánh diều | Giải Toán lớp 6

Giải Toán lớp 6 Cánh diều Bài 5: Số thập phân

Hoạt động 1 trang 44 Toán lớp 6 Tập 2: Viết các phân số 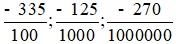dưới dạng số thập phân và đọc các số thập phân đó theo mẫu.

Mẫu: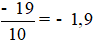 và được đọc là: âm một phẩy chín

Lời giải:

Các phân số được viết dưới dạng số thập phân là:

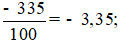
Đọc là: âm ba phẩy ba mươi lăm.

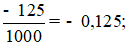
Đọc là: âm không phẩy một trăm hai lăm.

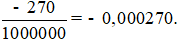
Đọc là: âm không phẩy không không không hai bảy không.

Lời giải Toán 6 Bài 5: Số thập phân hay, chi tiết khác:

Luyện tập 1 trang 45 Toán 6 Tập 2 Cánh diều | Giải Toán lớp 6

Giải Toán lớp 6 Cánh diều Bài 5: Số thập phân

Luyện tập 1 trang 45 Toán lớp 6 Tập 2: Viết các phân số và hỗn số sau dưới dạng số thập phân:

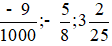
Lời giải:

Các phân số, hỗn số được viết dưới dạng số thập phân là:

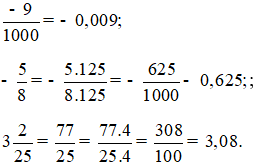
Lời giải Toán 6 Bài 5: Số thập phân hay, chi tiết khác:

Luyện tập 2 trang 45 Toán 6 Tập 2 Cánh diều | Giải Toán lớp 6

Giải Toán lớp 6 Cánh diều Bài 5: Số thập phân

Luyện tập 2 trang 45 Toán lớp 6 Tập 2: Viết các số thập phân sau dưới dạng phân số tối giản:

-0,125; -0,012; -4,005

Lời giải:

Viết các phân số dưới dạng phân số tối giản là:

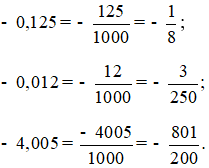
Lời giải Toán 6 Bài 5: Số thập phân hay, chi tiết khác:

Hoạt động 2 trang 46 Toán 6 Tập 2 Cánh diều | Giải Toán lớp 6

Giải Toán lớp 6 Cánh diều Bài 5: Số thập phân

Hoạt động 2 trang 46 Toán lớp 6 Tập 2: So sánh:

a) 508,99 và 509,01; 

b) 315,267 và 315,29.

Lời giải:

a) Vì 508 < 509 nên 508,99 < 509,01.

Vậy 508,99 < 509,01.

b) Ta có: 315 = 315 và kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần trăm. Do 6 < 9 nên 315,267 < 315,29.

Vậy 315,267 < 315,29.

Lời giải Toán 6 Bài 5: Số thập phân hay, chi tiết khác:

Hoạt động 3 trang 47 Toán 6 Tập 2 Cánh diều | Giải Toán lớp 6

Giải Toán lớp 6 Cánh diều Bài 5: Số thập phân

Hoạt động 3 trang 47 Toán lớp 6 Tập 2: Nêu cách so sánh hai số nguyên âm.

Lời giải:

Cách so sánh hai số nguyên âm a và b:

- Tìm số đối của hai số nguyên a và b.

- Ta sẽ so sánh số đối của hai số nguyên âm a và b với nhau (số nguyên âm nào có số đối lớn hơn thì sẽ nhỏ hơn).

Lời giải Toán 6 Bài 5: Số thập phân hay, chi tiết khác:

Luyện tập 3 trang 47 Toán 6 Tập 2 Cánh diều | Giải Toán lớp 6

Giải Toán lớp 6 Cánh diều Bài 5: Số thập phân

Luyện tập 3 trang 47 Toán lớp 6 Tập 2: Viết các số sau theo thứ tự giảm dần:

-120,341; 36,095; 36,1; -120,34.

Lời giải:

Ta sẽ chia các số thập phân trên thành hai nhóm:

- Nhóm 1 gồm các số thập phân âm: -120,341; -120,34.

- Nhóm 2 gồm các số thập phân dương: 36,095; 36,1.

Vì các số thập phân âm luôn nhỏ hơn các số thập phân dương nên ta chỉ cần so sánh các số trong từng nhóm với nhau.

Ở nhóm 1: Ta có số đối của số thập phân -120,341 là 120,341 và số đối của số thập phân – 120,34 là 120,34. Ta có: 120 = 120, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần nghìn. Do 1 > 0 nên 120,341 > 120,34 hay -120,341 < -120,34.

Ở nhóm 2: Ta có 36 = 36, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần mười. Do 0 < 1 nên 36,095 < 36,1.

Suy ra -120,341 < -120,34 < 36,095 < 36,1.

Vậy 36,1; 36,095; -120,34; -120,341.

Lời giải Toán 6 Bài 5: Số thập phân hay, chi tiết khác:

Bài 1 trang 47 Toán 6 Tập 2 Cánh diều | Giải Toán lớp 6

Giải Toán lớp 6 Cánh diều Bài 5: Số thập phân

Bài 1 trang 47 Toán lớp 6 Tập 2: Viết các phân số và hỗn số sau dưới dạng số thập phân: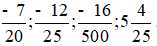

Lời giải:

Các phân số và hỗn số viết dưới dạng số thập phân là:

Lời giải Toán 6 Bài 5: Số thập phân hay, chi tiết khác:

Bài 2 trang 47 Toán 6 Tập 2 Cánh diều | Giải Toán lớp 6

Giải Toán lớp 6 Cánh diều Bài 5: Số thập phân

Bài 2 trang 47 Toán lớp 6 Tập 2: Viết các số thập phân sau dưới dạng phân số tối giản: - 0,225; - 0,033.

Lời giải:

Các số thập phân được viết dưới dạng phân số tối giản là:

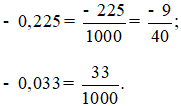
Lời giải Toán 6 Bài 5: Số thập phân hay, chi tiết khác:

Bài 3 trang 47 Toán 6 Tập 2 Cánh diều | Giải Toán lớp 6

Giải Toán lớp 6 Cánh diều Bài 5: Số thập phân

Bài 3 trang 47 Toán lớp 6 Tập 2: Viết các số sau theo thứ tự tăng dần:

a) 7,012; 7,102; 7,01; 

b) 73,059; - 49,037; - 49,307.

Lời giải:

a) Ta sẽ so sánh từng cặp số với nhau:

+) 7,012 và 7,102.

Ta có 7 = 7, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần mười. Do 0 < 1 nên 7,012 < 7,102 (1).

+) 7,012 và 7,01

Ta có 7 = 7, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần nghìn. Do 0 < 2 nên 7,012 > 7,01 (2).

Từ (1) và (2) suy ra: 7,01 < 7,012 < 7,102.

Vậy các số theo thứ tự tăng dần là: 7,01; 7,012; 7,102.

b) Vì số thập phân âm luôn bé hơn số thập phân dương nên ta chỉ cần so sánh -49,037 và -49,307.

Ta có số đối của số thập phân -49,037 là 49,037 và số đối của số thập phân -49,307 là 49,307.

Ta có: 49 = 49, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần mười. Do 0 < 3 nên 49,037 < 49,307 hay -49,037 > -49,307.

Suy ra: -49,307 < -49,037 < 73,059.

Vậy các số theo thứ tự tăng dần là: -49,307; -49,037; 73,059.

Lời giải Toán 6 Bài 5: Số thập phân hay, chi tiết khác:

Bài 4 trang 47 Toán 6 Tập 2 Cánh diều | Giải Toán lớp 6

Giải Toán lớp 6 Cánh diều Bài 5: Số thập phân

Bài 4 trang 47 Toán lớp 6 Tập 2: Viết các số sau theo thứ tự giảm dần:

a) 9,099; 9,009; 9,090; 9,990; 

b) - 6,27; - 6,207; - 6,027; - 6,277.

Lời giải:

a) Ta có: 9 = 9, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần mười. Do 0 < 9 nên 9,990 là số lớn nhất.

Các số còn lại, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần trăm. Do 0 < 9 nên 9,009 là số nhỏ nhất.

Hai số còn lại là 9,099; 9,090, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần nghìn. Do 0 < 9 nên 9,090 < 9,099.

Suy ra 9,009 < 9,090 < 9,099 < 9,990.

Vậy các số theo thứ tự giảm dần là: 9,990; 9,099; 9,090; 9,009.

b) Vì các số - 6,27; - 6,207; - 6,027; - 6,277 đều là số thập phân âm nên ta sẽ chuyển qua so sánh các số đối lần lượt là: 6,27; 6,207; 6,027; 6,277.

Ta có 6 = 6, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần mười. Do 0 < 2 nên số 6,027 là số nhỏ nhất.

Đối với các số còn lại 6,27; 6,207; 6,277, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần trăm. Do 0 < 7 nên 6,207 là số nhỏ nhất trong dãy này.

Còn lại hai số 6,27; 6,277, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần nghìn. Do 0 < 7 nên 6,27 < 6,277.

Suy ra 6,027 < 6,207 < 6,27 < 6,277 hay - 6,027 > - 6,207 > - 6,27 > - 6,277.

Vậy các số theo thứ tự giảm dần là: - 6,027; - 6,207; - 6,27; - 6,277.

Lời giải Toán 6 Bài 5: Số thập phân hay, chi tiết khác:

Bài 5 trang 47 Toán 6 Tập 2 Cánh diều | Giải Toán lớp 6

Giải Toán lớp 6 Cánh diều Bài 5: Số thập phân

Bài 5 trang 47 Toán lớp 6 Tập 2: Trong một cuộc thi chạy 200 m, có ba vận động viên đạt thành tích cao nhất là:

Mai Anh: 31,42 giây; Ngọc Mai: 31,48 giây; Phương Hà: 31,09 giây.

Vận động viên nào đã về nhất? Về nhì? Về ba?

Lời giải:

Ta cần so sánh thời gian hoàn thành cuộc đua của các vận động viên tham gia:

Ta có 31 = 31 = 31, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần mười. Do 0 < 4 nên 31,09 là số bé nhất.

Còn hai số còn lại 31,42 và 31,48, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở hàng phần trăm. Do 2 < 8 nên 31,42 < 31,48.

Từ đó suy ra: 31,09 < 31,42 < 31,48.

Vận động viên về nhất là vận động viên đến đích sớm hơn hay mất ít thời gian nhất để hoàn thành cuộc đua. Vận động viên về nhì là vận động viên mất ít thời gian tiếp theo. Vận động viên về ba là vận động viên mất nhiều thời gian nhất trong ba vận động viên.

Vậy vận động viên về nhất là bạn Phương Hà, vận động viên về nhì là bạn Mai Anh, vận động viên về ba là bạn Ngọc Mai.

Lời giải Toán 6 Bài 5: Số thập phân hay, chi tiết khác:

Sách bài tập Toán lớp 6 Bài 5: Số thập phân - Cánh diều

Giải sách bài tập Toán lớp 6 Bài 5: Số thập phân - Cánh diều

Với giải sách bài tập Toán lớp 6 Bài 5: Số thập phân sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 6.

Vở bài tập Toán 6 Bài 5: Số thập phân - Cánh diều

Với giải vở bài tập Toán lớp 6 Bài 5: Số thập phân sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập về nhà trong VBT Toán 6 Bài 5.

Giải vở bài tập Toán 6 Bài 5: Số thập phân - Cánh diều

I. Kiến thức trọng tâm

Số thập phân (Lý thuyết Toán lớp 6) | Cánh diều

Với tóm tắt lý thuyết Toán lớp 6 Bài 5: Số thập phân hay nhất, chi tiết sách Cánh diều sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 6.

Số thập phân (Lý thuyết Toán lớp 6) | Cánh diều

Lý thuyết Số thập phân

1. Số thập phân

- Phân số thập phân là phân số mà mẫu là lũy thừa của 10 và tử là số nguyên.

- Phân số thập phân có thể viết được dưới dạng số thập phân.

- Số thập phân gồm hai phần:

+ Phần số nguyên được viết bên trái dấu phẩy;

+ Phần thập phân được viết bên phải dấu phẩy.

Ví dụ 1. Viết các phân số và hỗn số sau dưới dạng số thập phân: $\frac{-27}{100};$ $\frac{1}{25};$   $1\frac{3}{125}$.

Hướng dẫn giải

$\frac{-27}{100}=-0,27;$

$\frac{1}{25}=\frac{1.4}{25.4}=\frac{4}{100}=0,04;$

$1\frac{3}{125}=1+\frac{3}{125}=1+\frac{3.8}{125.8}=1+\frac{24}{1000}=1+0,024=1,024.$

2. So sánh các số thập phân

a) So sánh hai số thập phân

Trong 2 số thập phân khác nhau luôn có một số nhỏ hơn số kia.

- Nếu số thập phân a nhỏ hơn số thập phân b thì ta viết a < b hay b > a.

- Số thập phân lớn hơn 0 gọi là số thập phân dương.

- Số thập phân nhỏ hơn 0 gọi là số thập phân âm.

- Nếu a < b và b < c thì a < c.

b) Cách so sánh hai số thập phân

* So sánh hai số thập phân khác dấu:

Số thập phân âm luôn nhỏ hơn số thập phân dương.

* So sánh hai số thập phân dương:

Bước 1: So sánh phần số nguyên của hai số thập phân dương đó. Số thập phân nào có phần số nguyên lớn hơn thì lớn hơn.

Bước 2: Nếu 2 số thập phân dương đó có phần số nguyên bằng nhau thì ta tiếp tục so sánh từng cặp chữ số ở cùng một hàng (sau dấu ","), kể từ trái sang phải cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số thập phân chứa chữ số đó lớn hơn.

* So sánh hai số thập phân âm:

Nếu a < b thì ‒ a > ‒ b.

Ví dụ 2. Sắp xếp các số thập phân 3,124; –3,105; –3,142; 3,015 theo thứ tự giảm dần.

Hướng dẫn giải

Ta chia các số 3,124; –3,105; –3,142; 3,015 thành hai nhóm:

Nhóm 1 gồm các số 3,124; 3,015.

Nhóm 2 gồm các số –3,105; –3,142.

Ta đi so sánh nhóm 1: 3,124; 3,015.

Kể từ trái sang phải, cặp chữ số đầu tiên khác nhau của hai số trên là hàng phần mười. Mà 1 > 0 nên 3,124 > 3,015.

Ta đi so sánh nhóm 2: –3,105; –3,142.

Xét hai số 3,105 và 3,142;

Kể từ trái sang phải, cặp chữ số đầu tiên khác nhau của hai số trên là hàng phần trăm. Mà 0 < 4 nên 3,105 < 3,142. Do đó –3,105 > –3,142.

Nhóm 1 gồm các số thập phân dương, nhóm 2 gồm các số thập phân âm, mà số thập phân dương luôn lớn hơn số thập phân âm.

Do đó 3,124 > 3,015 > –3,105 > –3,142.

Vậy sắp xếp các số theo thứ tự giảm dần là:  3,124; 3,015; –3,105; –3,142.

Bài tập Số thập phân

Bài 1: Cho các phân số và hỗn số: $\frac{-3}{10}$; $\frac{7}{-50};$ $1\frac{19}{125};$$\frac{27}{{10}^3}$; $\frac{7}{8}.$  

a) Viết các phân số và hỗn số trên dưới dạng phân số thập phân;

b) Sắp xếp các số thập phân tìm được ở câu a theo thứ tự tăng dần.

Hướng dẫn giải

a) Ta có: $\frac{-3}{10}=-\frac{3}{10}=-0,3$;

$\frac{7}{-50}=-\frac{7}{50}=-\frac{7.2}{50.2}=-\frac{14}{100}=-0,14$

$1\frac{19}{125}=1+\frac{19}{125}=\frac{125}{125}+\frac{19}{125}=\frac{144}{125}=\frac{144.8}{125.8}=\frac{1152}{1000}=1,152$;

$\frac{27}{{10}^3}=\frac{27}{1000}=0,027;$

$\frac{7}{8}=\frac{7.125}{8.125}=\frac{875}{1000}=0,875$

Vậy $\frac{-3}{10}=-0,3;\frac{7}{-50}=-0,14;1\frac{19}{125}=1,152;\frac{27}{{10}^3}=0,027;\frac{7}{8}=0,875$

b) Ta chia các số ‒0,3; ‒0,14; 1,152; 0,027; 0,875 thành hai nhóm:

Nhóm 1 gồm các số: ‒0,3; ‒0,14

Nhóm 2 gồm các số 1,152; 0,027; 0,875.

Ta đi so sánh nhóm 1: ‒0,3; ‒0,14

Xét hai số 0,3 và 0,14: Kể từ trái sang phải, cặp chữ số đầu tiên khác nhau của hai số trên là hàng phần mười. Mà 3 > 1 nên 0,3 > 0,14 do đó ‒0,3 < ‒0,14.

Ta đi so sánh nhóm 2: 1,152; 0,027; 0,875.

Xét hai số 0,027 và 0,875: Kể từ trái sang phải, cặp chữ số đầu tiên khác nhau của hai số này là hàng phần mười. Mà 0 < 8 nên 0,027 < 0,875.

Xét hai số 0,875 và 1,152: Ta thấy phần nguyên của hai số là 0 < 1 nên 0,875 < 1,152.

Suy ra 0,027 < 0,875 < 1,152

Nhóm 1 gồm các số âm và nhóm 2 gồm các số dương. Mà số âm luôn nhỏ hơn số dương.

Do đó ta có ‒0,3 < ‒0,14 < 0,027 < 0,875 < 1,152.

Vậy sắp xếp các số thập phân theo thứ tự tăng dần là  ‒0,3; ‒0,14; 0,027; 0,875; 1,152.

Bài 2: Viết các số thập phân sau dưới dạng phân số tối giản có mẫu số dương:

‒35,45; 0,79; ‒0,068.

Hướng dẫn giải

Ta có: ‒35,45 $=-\frac{3545}{100}=-\frac{3545:5}{100:5}=-\frac{709}{20}=\frac{-709}{20}$;

0,79 $=\frac{79}{100}$;

‒0,068 $=-\frac{68}{1000}=-\frac{68:4}{1000:4}=-\frac{17}{250}=\frac{-17}{250}$.

Bài 3: Biết nhiệt độ đông đặc của thuỷ ngân là ‒38,83°C, của rượu là ‒114,1°C, của băng phiến là 80,26°C và của nước là 0°C.

Hãy cho biết nhiệt độ đông đặc của chất nào là thấp nhất?

Hướng dẫn giải

Ta so sánh hai số ‒38,83 và ‒114,1:

Xét hai số 38,83 và 114,1 ta thấy phần nguyên của hai số là 38 < 114 nên 38,83 < 114,1 suy ra ‒38,83 > ‒114,1

Ta thấy nhiệt độ đông đặc của thuỷ ngân (‒38,83°C) và của rượu (‒114,1°C) là số thập phân âm; nhiệt độ đông đặc của băng phiến (80,26°C ) là số thập phân dương và của nước là số 0.

Mà số 0 luôn lớn hơn số thập phân âm và nhỏ hơn số thập phân dương.

Do đó ta có: ‒114,1 < ‒38,83  < 0 < 80,26

Hay ‒114,1°C < ‒38,83°C < 0°C < 80,26°C.

Vậy nhiệt độ đông đặc của rượu là thấp nhất.

Học tốt Số thập phân

Các bài học để học tốt Số thập phân Toán lớp 6 hay khác:

Bài tập trắc nghiệm Số thập phân (có đáp án) - Toán lớp 6 Cánh diều

Với 20 bài tập trắc nghiệm Toán lớp 6 Bài 5: Số thập phân có đáp án và lời giải chi tiết đầy đủ các mức độ sách Cánh diều sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 6.

Bài tập trắc nghiệm Số thập phân (có đáp án) - Toán lớp 6 Cánh diều

Câu 1. Viết phân số $\frac{131}{1000}$ dưới dạngsố thập phân ta được

A. 0,131

B. 0,1331

C. 1,31

D. 0,0131

Hiển thị đáp án

Trả lời:

$\frac{131}{1000}=\mathrm{0,131}$

Đáp án cần chọn là: A

Câu 2. Viết số thập phân 0,25 về dạng phân số ta được:

A.$\frac{1}{4}$

B.$\frac{5}{2}$

C.$\frac{2}{5}$

D.$\frac{1}{5}$

Hiển thị đáp án

Trả lời:

$\mathrm{0,25}=\frac{25}{100}=\frac{1}{4}$

Đáp án cần chọn là: A

Câu 3. Các phân số $\frac{69}{1000};8\frac{77}{100};\frac{34567}{{10}^4}$ được viết dưới dạng số thập phân theo lần lượt là

A. 0,69; 0,877; 3,4567

B. 0,69; 8,77; 3,4567

C. 0,069; 0,877; 3,4567

D. 0,069; 8,77; 3,4567

Hiển thị đáp án

Trả lời:

$$\begin{gathered} \frac{69}{1000}=\mathrm{0,069} \\ 8\frac{77}{100}=\frac{877}{100}=\mathrm{8,77} \\ \frac{34567}{{10}^4}=\mathrm{3,4567} \end{gathered}$$

Vậy các số thập phân viết theo thứ tự là 0,069; 8,77; 3,4567

Đáp án cần chọn là: D

Câu 4. Viết các phân số và hỗn số sau dưới dạng số thập phân:

$\frac{-9}{1000}=\mathrm{...};\frac{-5}{8}=\mathrm{...};3\frac{2}{25}=\mathrm{...}$

A. −0,09; −0,625; 3,08

B. −0,009; −0,625; 3,08

C. −0,9; −0,625; 3,08

D. −0,009; −0,625; 3,008

Hiển thị đáp án

Trả lời:

$\frac{-9}{1000}=-\mathrm{0,009};\frac{-5}{8}=\frac{-5.125}{8.125}=\frac{-625}{1000}=-\mathrm{0,625};3\frac{2}{25}=3\frac{8}{100}=\mathrm{3,08}$

Đáp án cần chọn là: B

Câu 5. Viết các số thập phân sau dưới dạng phân số tối giản:

−0,125=…; −0,012=...; −4,005=...

A.$\frac{-1}{8};\frac{-3}{250};\frac{-4005}{1000}$

B.$\frac{-1}{8};\frac{-3}{25};\frac{-801}{200}$

C.$\frac{-1}{4};\frac{-3}{250};\frac{-801}{200}$

D.$\frac{-1}{8};\frac{-3}{250};\frac{-801}{200}$

Hiển thị đáp án

Trả lời:

$$\begin{gathered} -\mathrm{0,125}=\frac{-125}{1000}=\frac{-125:125}{1000:125}=\frac{-1}{8} \\ -\mathrm{0,012}=\frac{-12}{1000}=\frac{-12:4}{1000:4}=\frac{-3}{250} \\ -\mathrm{4,005}=\frac{-4005}{1000}=\frac{-4005:5}{1000:5}=\frac{-801}{200} \end{gathered}$$

Đáp án cần chọn là: D

Câu 6.

Điền dấu ">;<;=" vào ô trống

508,99…….509,01

Hiển thị đáp án

Trả lời:

Ta có: 508 < 509 nên 508,99 < 509,01

Câu 7. Viết các số sau theo thứ tự giảm dần: −120,341; 36,095; 36,1; −120,34.

A. 36,095 > 36,100 > −120,34 > −120,341

B. 36,095 > 36,100 > −120,341 > −120,34

C. 36,100 > 36,095 > −120,341 > −120,34

D. 36,100 > 36,095 > −120,34 > −120,341

Hiển thị đáp án

Trả lời:

Ta có:

36,100 > 36,095 nên 36,1 > 36,095

−120,340 > −120,341 nên −120,34 > −120,341

⇒ 36,100 > 36,095 > −120,34 > −120,341.

Đáp án cần chọn là: D

Câu 8

Trong một cuộc thi chạy 200 m, có ba vận động viên đạt thành tích cao nhất là:

Mai Anh: 31,42 giây; Ngọc Mai: 31,48 giây; Phương Hà: 31,09 giây.

Các vận động viên đã về Nhất, về Nhì, về Ba lần lượt là:

A. Ngọc Mai, Mai Anh, Phương Hà.

B. Ngọc Mai, Phương Hà, Mai Anh.

C. Phương Hà, Mai Anh, Ngọc Mai.

D. Mai Anh, Ngọc Mai, Phương Hà.

Hiển thị đáp án

Trả lời:

Ta có: 31,48 > 31,42 > 31,09.

Suy ra Ngọc Mai về nhất, Mai Anh về nhì, Phương Hà về ba.

Đáp án cần chọn là: A

Câu 9. Số đối của các số thập phân sau lần lượt là: 9,32; −12,34; −0,7; 3,333

A. 9,32; −12,34; −0,7; 3,333

B. −9,32; 12,34; 0,7; 3,333

C. −9,32; 12,34; 0,7; −3,333

D. −9,32; −12,34; 0,7; −3,333

Hiển thị đáp án

Trả lời:

Số đối của 9,32 là −9,32

Số đối của −12,34 là 12,34

Số đối của −0,7 là 0,7

Số đối của 3,333 là −3,333

Vậy ta được: −9,32; 12,34; 0,7; −3,333

Đáp án cần chọn là: C

Câu 10.

Cho các câu sau:

(1) Đọc dấu phẩy

(2) Đọc phần nguyên

(3) Đọc phần thập phân

Thứ tự các bước để đọc một số thập phân là:

A. (1)→(2)→(3)

B. (3)→(1)→(2)

C. (2)→(1)→(3)

D. (3)→(2)→(1)

Hiển thị đáp án

Trả lời:

Muốn đọc một số thập phân, ta đọc lần lượt từ hàng cao đến hàng thấp: trước hết đọc phần nguyên, đọc dấu “phẩy”, sau đó đọc phần thập phân.

Vậy thứ tự các bước để đọc một số thập phân là(2)→(1)→(3)

Câu 11.

Mỗi đơn vị của một hàng bằng bao nhiêu đơn vị của hàng thấp hơn liền sau?

A. 0,01 đơn vị

B. 0,1 đơn vị

C. 10 đơn vị

D. 100 đơn vị

Hiển thị đáp án

Trả lời:

Mỗi đơn vị của một hàng bằng 1010 đơn vị của hàng thấp hơn liền sau.

Câu 12.

Số thập phân 0,06 đọc là:

A. Không phẩy sáu

B. Không phẩy không sáu

C. Không phẩy không không sáu

D. Không phẩy không.

Hiển thị đáp án

Trả lời:

Số thập phân 0,06 đọc là không phẩy không sáu.

Câu 13.

Cho số thập phân 48,15. Chữ số 5 thuộc hàng nào?

A. Hàng chục

B. Hàng đơn vị

C. Hàng phần mười

D. Hàng phần trăm

Hiển thị đáp án

Trả lời:

Trong số thập phân 48,15 chữ số 5 thuộc hàng phần trăm.

Câu 14.

Kéo thả số thập phân thích hợp vào ô trống:

28,905

28,95

28,915

Số thập phân có hai chục, tám đơn vị, chín phần mười, không phần trăm, năm phần nghìn viết là

Hiển thị đáp án

Trả lời:

Số thập phân có hai chục, tám đơn vị, chín phần mười, không phần trăm, hai phần nghìn viết là28,905.

Câu 15.

A. Nếu viết thêm chữ số 0 vào bên phải phần thập phân của một số thập phân thì được một số thập phân bằng nó.

B. Nếu một số thập phân có chữ số 0 ở tận cùng bên phải phần thập phân thì khi bỏ chữ số 0 đó đi, ta được một số thập phân bằng nó.

C. Cả A và B đều đúng.

D. Cả A và B đều sai.

Hiển thị đáp án

Trả lời:

Nếu viết thêm chữ số 0 vào bên phải phần thập phân của một số thập phân thì được một số thập phân bằng nó.

Nếu một số thập phân có chữ số 0 ở tận cùng bên phải phần thập phân thì khi bỏ chữ số 0 đó đi, ta được một số thập phân bằng nó.

Vậy cả A vàB đều đúng.

Câu 16.

Kéo thả dấu thích hợp vào ô trống:

>

<

=

27,345........30,01

Hiển thị đáp án

Trả lời:

Ta thấy hai số đã cho có phần nguyên là 27 và 30.

Mà 27 < 30 nên27,345 < 30,01

Vậy đáp án cần điền là dấu: <.

Câu 17.

Điền số thích hợp vào ô trống:

Cho các số thập phân sau: 14,35; 31,45; 51,34; 13,54; 43,15

Số thập phân lớn nhất trong 5 số đã cho là ........

Hiển thị đáp án

Trả lời:

Xét phần nguyên của các số đã cho ta có: 13 < 14 < 31 < 43 < 51

Nên: 13,54 < 14,35 < 31,45 < 43,15 < 51,34.

Do đó số thập phân lớn nhất trong 5 số đã cho là51,34.

Vậy đáp án cần điền vào ô trống là 51,34.

Câu 18.

Sắp xếp các số sau theo thứ tự từ bé đến lớn:

5,36; 13,107; 0,28; 28,105; 13,4

A. 0,28; 5,36; 13,4; 13,107; 28,105

B. 0,28; 5,36; 13,4; 28,105; 13,107

C. 0,28; 5,36; 13,107; 13,4; 28,105

D. 28,105; 13,4; 13,107; 5,36; 0,28

Hiển thị đáp án

Trả lời:

Xét phần nguyên của các số đã cho ta có: 0 < 5 < 13 < 28.

Mà hai số 13,107; 13,4 có cùng phần nguyên là 13.

Xét phần mười của hai số ta có 1 < 4 nên 13,107 < 13,4

Do đó 0,28 < 5,36 < 13,107 < 13,4 < 28,105

Vậy các số được viết theo thứ tự từ bé đến lớn là 0,28; 5,36; 13,107; 13,4; 28,105

Câu 19.

Tìm chữ số a, biết 97,614 < 97,a12(a < 8)

A. a = 3

B. a = 4

C. a = 6

D. a = 7

Hiển thị đáp án

Trả lời:

Để số thập phân 97,614 < 97,a12(a < 8) khi hai số có cùng phần nguyên (97 = 97), cùng hàng phần trăm (1 = 1) và có hàng phần nghìn khác nhau (4 > 2) thì chữ số a đứng ở hàng phần mười phải lớn hơn 6 ( vì ở hàng phần mười của số 97,614 là chữ số 6).

Theo bài ra ta có: 6 < a < 8.

Vì 6 < 7 < 8 nên suy ra a = 7.

Câu 20.

Điền số thích hợp vào ô trống:

Viết thêm các chữ số 00 vào bên phải phần thập phân của số thập phân sau để phần thập phân có 4 chữ số:

157,24 =.......

Hiển thị đáp án

Trả lời:

Khi viết thêm bao nhiêu chữ số 00 vào bên phải phần thập phân của một số thập phân thì ta vẫn được một số thập phân bằng nó.

Theo đề bài, phần thập phân của số thập phân mới có 4 chữ số, mà phần thập phân của số thập phân đã cho có 2 chữ số nên ta cần thêm vào 2 chữ số 0.

Do đó ta có: 157,24 = 157,2400

Vậy đáp án cần điền vào ô trống là 157,2400.

Xem thêm bài tập trắc nghiệm Toán lớp 6 Cánh diều có đáp án hay khác: