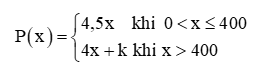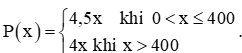Vận dụng 1 trang 82 Toán 11 Tập 1 Chân trời sáng tạo

Giải Toán 11 Bài 3: Hàm số liên tục - Chân trời sáng tạo

Vận dụng 1 trang 82 Toán 11 Tập 1: Tại một xưởng sản xuất bột đá thạch anh, giá bán (tính theo nghìn đồng) của x (kg) bột đá thạch anh được tính theo công thức sau:

(k là một hằng số).

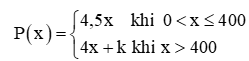
a) Với k = 0, xét tính liên tục của hàm số P(x) trên (0; +∞).

b) Với giá trị nào của k thì hàm số P(x) liên tục trên (0; +∞)?

Lời giải:

a) Với k = 0, hàm số

+) Lấy x₀ ∈ (0; 400) khi đó P(x) = 4,5x

Suy ra $\underset{x\to x_0}{\lim }P\left(x\right)=\underset{x\to x_0}{\lim }\left(4,5x\right)=4,5x_0=P\left(x_0\right)$

Do đó P(x) liên tục trên (0; 400).

+) Tại x₀ = 400, ta có:

$\underset{x\to {400}^{-}}{\lim }P\left(x\right)=\underset{x\to {400}^{-}}{\lim }\left(4,5x\right)=4,5.400=1800$.

$\underset{x\to {400}^{+}}{\lim }P\left(x\right)=\underset{x\to {400}^{+}}{\lim }\left(4x\right)=4.400=1600$.

Suy ra $\underset{x\to {400}^{-}}{\lim }P\left(x\right)\ne \underset{x\to {400}^{+}}{\lim }P\left(x\right)$. Do đó không tồn tại $\underset{x\to 400}{\lim }P\left(x\right)$.

Vì vậy hàm số không liên tục tại x = 400.

+) Lấy x₀ ∈ (400; +∞) khi đó P(x) = 4x

Suy ra $\underset{x\to x_0}{\lim }P\left(x\right)=\underset{x\to x_0}{\lim }\left(4x\right)=4x_0=P\left(x_0\right)$

Do đó P(x) liên tục trên (400; +∞) .

Vậy hàm số liên tục trên (0; 400) và (400; +∞).

b) Để hàm số P(x) liên tục trên (0; +∞) thì P(x) phải liên tục trên x₀ = 400.

Do đó $\underset{x\to {400}^{-}}{\lim }P\left(x\right)=\underset{x\to {400}^{+}}{\lim }P\left(x\right)\iff 1800=4.400+k\iff k=200$.

Vậy với k = 200 thì hàm số liên tục trên (0; +∞).

Lời giải bài tập Toán 11 Bài 3: Hàm số liên tục hay, chi tiết khác: